INTRODUCCIÓN
La relación que se establece entre dos o más conjuntos de datos de distintas variables se conoce como función matemática. Una función se utiliza para expresar la dependencia entre dos magnitudes, donde una de ellas es la variable dependiente y otra la variable independiente, y su relación puede representar la vida real con modelos matemáticos lineales de diferente orden (primer, segundo, tercer, etc.), de tal manera que parámetros como la pendiente y la ordenada al origen (Aguilar, Bravo, Gallegos, Cerón & Reyes, 2009) ayudan en la comprensión del comportamiento de fenómenos naturales o distintos procesos que ocurren en la naturaleza.
La ingeniería de riego agrícola tiene variables que deben ser estimadas e interpretadas para responder a la pregunta ¿cuándo y cuánto regar? Una de estas variables es la evapotranspiración (ET), definida como la suma del agua evaporada de la superficie del suelo y el agua transpirada por un cultivo (Allen, Pereira, Raes & Smith, 2006), y se considera como la principal limitante de los sistemas de producción agrícola (Andrew & Shashi, 2009), de tal manera que en zonas áridas y semiáridas del mundo, donde el agua es un recurso poco disponible en el suelo, es un factor crítico en la productividad de los cultivos (Liu, Shenjiao, Shiqing, Xinping & Fang, 2010). Una variable que sirve como indicador de la producción de los cultivos es el índice de área foliar (IAF), que se define como el área proyectada por las hojas del cultivo por unidad de superficie del suelo (Jones, 1992), de tal modo que el incremento de este índice en un cultivo permite inferir una mayor intercepción de radiación solar y, por ende, el incremento del proceso fotosintético, el cual se refleja en un aumento en el rendimiento (Yang et al., 2004). Otra variable que se puede calcular y que está relacionada con la ET es la eficiencia en el uso del agua (EUA), la cual se puede entender como el volumen de agua que las plantas necesitan consumir para incorporar a su biomasa una determinada cantidad de carbono (CO2) proveniente de la atmósfera (Medrano et al., 2007). La EUA es el cociente de la división del peso de materia seca (MS) entre el volumen de agua aplicado, por lo que sus unidades son Kg m-3, aunque en ocasiones se expresa en unidades de peso por unidad de superficie por lámina de agua (g m-2 mm-1) (Howell, Tolk, Schneider & Evett, 1998).
Existen diferentes alternativas para incrementar el IAF y la EUA en la agricultura. Una de ellas es el manejo del cultivo mediante la utilización de acolchados plásticos, que constituyen la segunda aplicación en importancia después de los invernaderos. La superficie mundial bajo esta modalidad es de 4 530 000 ha, y destacan los países como China con 2 000 000 ha, Japón con 150 000 ha, Francia y España con 100 000 ha. Su importancia es muy variada, y en ella se enfatizan mayor producción y calidad de la cosecha, la precocidad de los cultivos, mayor eficiencia en el uso del agua, aumento en la temperatura del suelo y control de malezas entre otros (Kasirajan & Ngouajio, 2012).
Conocer la relación entre estas variables permite identificar las prácticas de manejo, para maximizar eluso y manejo del agua en un cultivo (Bradley, Hansen, Brummer & Pritchett, 2011). Por lo anterior, el objetivo de este trabajo fue evaluar dos estudios de caso con maíz forrajero, en el primero establecer la relación de las variables lámina (EV y agua aplicada) en función del tiempo y a cielo abierto, en el segundo estudio relacionar la producción de MS con el IAF en maíz forrajero con y sin acolchado plástico a través del tiempo, con el fin de comprender el fenómeno que se presenta en los dos ensayos evaluados.
MATERIALES Y MÉTODOS
Grupos de datos de variables fueron obtenidos de dos estudios de caso. Los estudios se llevaron a cabo en diferentes años (2006 y 2012) con maíz forrajero, en la Comarca Lagunera, que se encuentra entre los estados de Coahuila y Durango, México, entre los paralelos 24° 22’ y 26° 23’ de latitud Norte y entre los meridianos 101° 41’ a 104° 61’ de longitud Oeste, tiene una superficie de 47 887 km2, a 1120 msnm, con una extensión montañosa y una superficie plana donde se localiza el área agrícola. Su clima es un Bw (h’) hw (e), que corresponde seco desértico cálido, con lluvias en verano e invierno fresco, la precipitación pluvial media anual es 258 mm y la evaporación media anual es 2000 mm, por lo cual la relación precipitación-evaporación es 1:10; la temperatura media anual es 21 °C con máxima de 33.7 °C y mínima 7.5 °C (García, 1988). Los experimentos fueron establecidos en suelos de textura franco y franco arenoso, con una capacidad de retención de humedad promedio de 0.18 g de agua gr suelo-1.
La investigación se dividió en tres partes: 1) análisis de la EV y agua aplicada (LR) en maíz forrajero a través del tiempo, 2) estudio del comportamiento de la MS e IAF de maíz forrajero con y sin acolchado plástico a través del tiempo y 3) evaluación de los datos de las variables.
Análisis de la EV y LR en maíz forrajero
El conjunto de datos de las variables EV y LR se obtuvieron un estudio realizado con maíz forrajero durante el ciclo primavera-verano del 2006, en la pequeña propiedad el Cercado, ubicada en la carretera Torreón- San Pedro km 7.5. La EV se midió en un tanque evaporímetro tipo A (Allen et al., 2006) y se registraron diariamente por la mañana (9:00 a.m.). La LR que se aplicó fue estimada en función de la lámina evaporada del tanque y un coeficiente de cultivo, la cual se aplicó con un sistema de riego por goteo sub-superficial tipo cintilla, con un gasto de cinco L h-1 por metro lineal.
Los goteros fueron espaciados a 0.2 m y los tiempos de riego de tres a cuatro horas en promedio cada tercer día. La lámina de riego se contabilizó con un medidor de volumétrico instalado en el sistema de riego (Montemayor et al., 2012). Determinación del comportamiento de MS e IAF en maíz forrajero. El grupo de datos de MS e IAF se colectaron de un cultivo que se estableció en el ciclo primavera-verano del 2012, en la pequeña propiedad Esmeralda, ubicada en el municipio de Gómez Palacio Durango, México. En esta parte de la investigación, las variables en estudio fueron evaluadas en dos sistemas de producción: uno con la utilización de acolchado plástico (CA) y el segundo sin acolchado (SA). La MS se obtuvo mediante la selección de cuatro plantas del cultivo en forma aleatoria; el peso fresco de cada planta fue registrado. Posteriormente, en laboratorio las plantas se sometieron a secado hasta peso constante y se calculó el porcentaje de MS; finalmente se dedujo el peso promedio por planta; esta actividad se realizó semanalmente. El IAF se midió cada semana con el equipo LAI 2000 Plant Canopy Analyzer (LI-COR, Inc. Lincoln, Nebraska, EE.UU), aplicando la metodología indicada en el manual por el fabricante. Esta consistió en tomar una lectura en la parte superior del dosel del cultivo y cuatro lecturas en la parte inferior del mismo. Se realizaron cuatro repeticiones en lugares elegidos al azar dentro del campo del cultivo.
Evaluación de las variables
La evaluación de resultados de las variables consistió en establecer relaciones entre ellas mediante un análisis de regresión. La EV y LR de la primera parte de la investigación se consideraron como variables dependientes y se relacionaron con los días después de la siembra del cultivo (dds) como variable independiente, asumiendo una función lineal sin ordenada al origen, toda vez que la humedad del suelo y la EV al inicio del experimento se consideraron como cero, por ello el modelo matemático que se expresa en la ecuación 1:
donde Yij es la variable dependiente, Xi variable independiente, βi pendiente de la recta, con eij errores del modelo con media cero y varianza uno.
Para la segunda parte se estableció una relación entre la MS y el IAF (variables dependientes e independiente, respectivamente) mediante la función linealsimple como se plateó en la ecuación 1, en el sistema con acolchado y sin acolchar. Finalmente, una relación entre el grupo de datos de IAF (variable dependiente) y dds (variable independiente), para obtener una función polinomial, con el fin de generar un modelo como la ecuación de segundo grado 2.
donde Yij es la variable dependiente, β0 es la ordenada al origen, Xi variable independiente, βi pendiente de la recta, βi i coeficiente cuadrático, con eij errores del modelo con media cero y varianza uno.
Cada una de las regresiones se generó con el programa Excel del software Office 2010.
DISCUSIÓN Y RESULTADOS
Modelos de agua aplicada y evaporada con riego sub-superficial
Los modelos matemáticos de LR y EV con respecto a los dds (0 ≤ X ≤ 85) en el primer caso de estudio son estadísticamente significativos (p ≤ 0.05) y tienen una tendencia lineal positiva (figura 1), con una R2 > 0.95, lo que significa que los dds explican un 97.8% y un 99.9% el comportamiento de la LR y la EV, respectivamente.
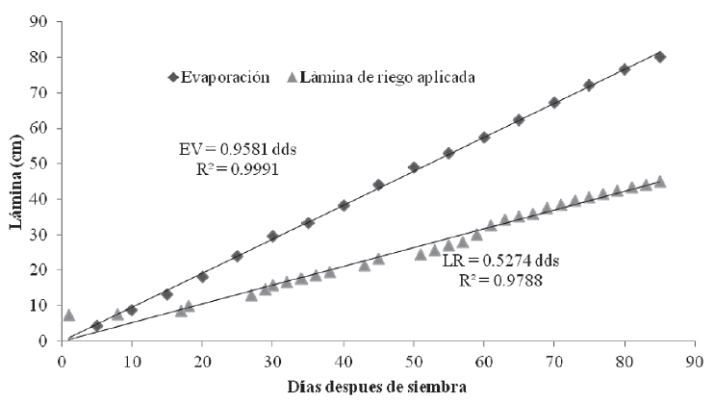
Fuente: Montemayor et al. (2012).
Figura 1 Modelos de lámina de agua aplicada y evaporada en función de los días después de siembra en un cultivo de maíz con riego subsuperficial.
Para la LR, la pendiente del modelo (figura 1) indica que por día transcurrido la lámina de riego aumentó 0.52 cm, mientras que la evaporación por cada día que transcurrió se acumuló a razón de 0.95 cm; es decir, se evaporó cerca del doble de que la LR diaria. En este sentido, Mena, Tijerina, Acosta & Mejía (2010) mencionaron que las láminas de aplicación de agua diarias para maíz pueden variar de 0.37 cm a 0.5 cm. En cambio, la evaporación al día puede variar de 0.6 cm a 1.0 cm en cultivos de maíz, lo cual cambia en función del ciclo de cultivo (Howell et al., 1998). Sin embargo, el déficit hídrico que podría presentarse por efecto de la evaporación no se detectó. Al respecto, se sabe que el cociente de la división de las pendientes de LR entre EV se define como coeficiente de cultivo o de cosecha (Kc) e indica el nivel de la satisfacción del agua al cultivo, el cual también depende de la forma de aplicación del agua por el sistema de irrigación (Montemayor et al., 2012). Andrew & Shashi (2009) reportaron valores de Kc de 1.03 ± 0.07; mientras que para condiciones de agricultura de secano los valores son de 0.84 ± 0.20. Al analizar la relación de las pendientes de las ecuaciones de LR y EV, el valor de Kc de nuestro estudio es de 0.55, menor que los reportados en la literatura; lo que nos lleva a deducir que este resultado es por efecto del sistema de riego superficial que se utilizó en el estudio que se analizó.
Materia seca producida en función del índice de área foliar en maíz forrajero en un suelo con y sin acolchado plástico
Las relaciones entre la MS y el IAF en el maíz forrajero con acolchado y sin acolchado (MSca-IAFca y MSsa- IAFsa), en el segundo caso de estudio, dieron como resultado modelos con pendientes positivas y coeficientes de determinación mayores que 0.9 (figura 2).
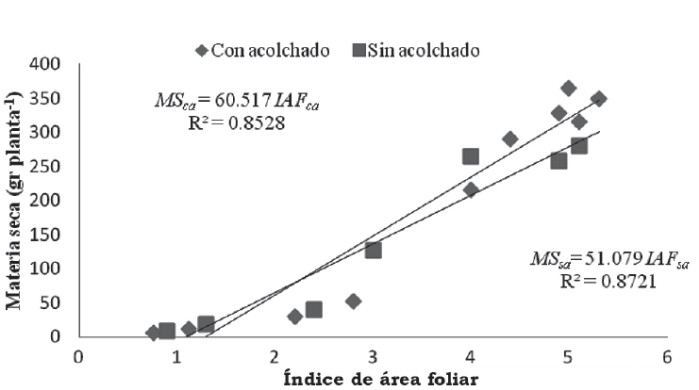
Fuente: Elaboracion propia.
Figura 2 Modelos de regresión lineal obtenidos de la producción de materia seca por planta en función del índice de área foliar.
De acuerdo con Adekayode & Olojugba (2010), el IAF es un importante parámetro para la intercepción de luz solar por el cultivo, ya que reportaron una relación positiva de 0.97 en la producción de maíz en grano e índice de área foliar. Por su parte, Zhang, Pingru, Xueyun, Zhaohui & Xinping (2011) concluyeron que un mayor IAF proporciona una mayor acumulación de biomasa, lo que se traduce en un incremento en la producción de grano en el cultivo de maíz.
Asimismo, Reta, Cueto, Gaytan & Santamaria (2007) concluyeron que el incremento de MS se debe al aumento del IAF que se observa en etapas tempranas del cultivo, acumulandose en tallos y hojas; lo anterior lo determinaron al establecer funciones lineales entre la producción de MS y el IAF con R 2 = 0.8528 y 0.8721, respectivamente. En nuestra investigación, al analizar el modelo que se obtuvo con acolchado, se tiene que la tasa de incremento (pendiente en la ecuación) de la MSca es de 60.52 g por planta cada vez que el IAFca aumente una unidad; mientras que para la MSsa la pendiente es menor, lo que representó una ganancia en peso por planta del orden de 18.48% en el sistema con acolchado con respecto al sistema sin acolchar. Lo anterior permite deducir que bajo las condiciones de producción similares los modelos serían útiles para estimar el contenido de MS al conocer el IAF.
Índice de área foliar en función de los días después de siembra en un suelo con y sin acolchado
El comportamiento del IAF con respecto a los dds es sigmoidal (figura 3) en los sistemas de producción con alcochado y sin acolchar; es decir, las relaciones que se establecieron entre las variables dependientes (IAFca e IAFsa) y la independiente (dds) tuvieron como resultados modelos polinomiales o ecuación cuadráticas.
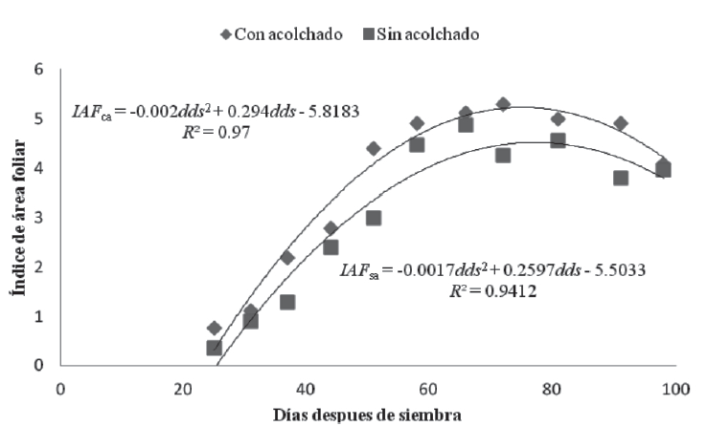
Fuente: Elaboracion propia.
Figura 3 Modelos obtenidos del índice de área foliar en maíz forrajero en un suelo con y sin acolchar.
El resultado anterior es un comportamiento típico delIAF, ya que este inicia con un crecimiento lento, seguido de un desarrollo rápido (etapa vegetativa), hasta que se alcanza un valor máximo, y posteriormente disminuye por la senescencia de las hojas, dado que las plantas alcanzan su madurez fisiológica (Guevara, Barcenas, Salazar, González & Suzán, 2005; Lukombo, Kizungu, Nkongolo, Lufuluabo & Tsumbu, 2013). En ambos sistemas de producción, el mayor IAF coincide con la etapa de floración del cultivo, la cual ocurre entre los 65 y 75 días después de la siembra; los valores estimados de IAF fueron de cinco para acolchado y de cuatro para el sistema sin acolchar. El cálculo del IAF es importante para estimar la intercepción de la luz por el cultivo, transpiración y acumulación de biomasa (Setiyono et al., 2007). El modelo correspondiente al sistema con acolchado presenta un crecimiento lineal diario de IAF de 0.294, mientras que sin acolchar este valor es de 0.259, lo que representa un 12% menos de crecimiento con respecto al sistema de acolchado. Montemayor et al. (2012) reportaron valores de 0.251, 0.155 y 0.106 para maíz irrigado con riego subsuperficial, pivote central y gravedad, respectivamente. La parte cuadrática de los modelos obtenidos refleja la estabilización del crecimiento del IAF durante el periodo de floración, como lo indicaron Guevara et al. (2005) y Montemayor et al. (2007). Mientras que Jones (1992) mencionó que la caída de la curva refleja la senescencia de las hojas del cultivo, las cuales provocan el decremento de reflectancia por el cultivo y, por consiguiente, una disminución del IAF. Los resultados de nuestro análisis muestran nuevamente las ventajas de utilizar acolchado, puesto que el crecimiento lineal es mayor que sin acolchar e incluso a lo reportado en la literatura como se mencionó anteriormente; asimismo, el valor del coeficiente del componente cuadrático en el acolchado es ligeramente mayor que sin acolchar.
Los modelos anteriores podrían ser útiles en la estimación del IAF con solo conocer los días después de la siembra, siempre y cuando el cultivo se establezca bajo las condiciones en que se llevaron a cabo en los ensayos correspondientes.
CONCLUSIONES
La herramienta matemática regresión lineal permite generar modelos que ayudan a entender, cuantificar y estimar variables en la ingeniería del riego como lámina de riego y evaporación, para cultivos como el maíz forrajero. Asimismo, se pueden establecer funciones que ayudan a la estimación de materia seca de este cultivo a partir del conocimiento del IAF y, a su vez, ecuaciones polinómicas para predecir el IAF a partir de los días después de la siembra. No obstante, se requiere de un mayor número de ensayos para verificar la validez de los modelos que en este estudio se plantearon, con la finalidad de dar certidumbre a dichas ecuaciones.











 nueva página del texto (beta)
nueva página del texto (beta)


