Introducción
La pregunta de cómo una economía asigna el uso de su espacio para organizar su actividad económica -léase cómo decide dónde producir, dónde consumir y dónde conciliar esas otras dos actividades-, ha sido escasamente abordada por la disciplina económica pese a su importancia intuitiva.1 La búsqueda de las razones de tal silencio va más allá del alcance de este escrito. Nuestro esfuerzo pretende, más bien, contribuir a responder dicha pregunta inspirándonos, como es habitual para la literatura relacionada, en el modelo seminal de von Thünen (1826).2
Como es sabido, este autor teorizó acerca del ordenamiento espacial de una economía descentralizada en la cual los productores (agricultores) decidían las producciones de sus terrenos (agrícolas). En particular, él supuso que cada productor sopesaba las productividades, los precios, los costos de producción y los costos de transporte de los diferentes cultivos potenciales hasta decidir qué productos producía y ofrecía efectivamente a la ciudad que abastecía, tratando de maximizar la rentabilidad de lo producido en su terreno. Para el supuesto de una ciudad única abastecida por terrenos de un territorio circundante homogéneo y aislado de lo demás, von Thünen dedujo que la economía tendía a un patrón de anillos concéntricos de producción, con un gradiente espacial de rentas de los terrenos en descenso monotónico desde las inmediaciones de la ciudad hasta la periferia del territorio.
Formalmente, la teoría de von Thünen se refiere a la rentabilidad de producir en un centro de producción (un terreno) y transportar lo producido a un centro de consumo (una ciudad), afirmando que tal rentabilidad (u) depende de la productividad del terreno para lo producido (r), del precio de lo producido (p), de su costo de producción en el terreno (c), de su tasa de transporte desde el terreno hasta la ciudad (C), y de la distancia entre ambos centros (x), según:
El argumento medular de la teoría es que, desagregando lo producido en productos diversos, el costo de transporte según la tasa de transporte y la distancia necesita balancearse si se quiere maximizar la rentabilidad estacionariamente. Esta necesidad de balance dicta, por ejemplo, que los productos para los cuales la tasa de transporte es mayor se puedan producir sólo donde la distancia es suficientemente menor (más cerca de la ciudad, donde los precios de los terrenos son mayores); pero el costo de producción, el precio y la productividad también intervienen. A la postre, el balance se resuelve decidiendo que en x se debe producir exclusivamente los productos de la especie cuya rentabilidad ahí es la máxima entre las de todos los productos potenciales.
Según Fujita, Krugman y Venables (1999), la teoría de von Thünen se soterró en un largo anonimato hasta que Alonso (1964) la hizo rebrotar sustituyendo a los agricultores por viajeros y a la ciudad por un distrito de negocios. Ese llamado “modelo mono-céntrico” dio como resultado los mismos anillos concéntricos para el uso del territorio que el de von Thünen, y se ha convertido en una pieza clave de la literatura empírica y teórica relacionada. Sin embargo, tanto el escrito de von Thünen como el de Alonso adolecen al menos de dos limitaciones importantes. Una es que ambos escritos suponen la existencia exógena de un centro -ya sea una ciudad o un distrito de negocios-, sin considerar un surgimiento endógeno de ese centro, a la par con el uso del territorio. Y la otra es que ambos describen las propiedades de la economía en estado estacionario, sin mostrar cómo se tendería a ese estado con el tiempo, y en qué condiciones. Respecto a la segunda limitación, Day y Tinney (1969) plantearon un modelo dinámico en el cual los agricultores desconocen las demandas y los precios estacionarios, y ofrecen sus productos agrícolas intermitente y sincrónicamente, una vez cada año, de manera que hasta las demandas y los precios momentáneos son difíciles de conocer cabalmente antes de que caduquen. Los autores resolvieron el modelo mediante simulaciones numéricas según las cuales, aún en las condiciones descritas, las rentas de los terrenos decaen desde la ciudad hasta la periferia del territorio, como predijo von Thünen. Más tarde, Okabe y Kune (1983) plantearon otro modelo dinámico parecido, que resolvieron mediante maniobras analíticas a base de representaciones gráficas, y mostraron la estabilidad del modelo en un escenario, su periodicidad en otro y su inestabilidad en varios otros. Más recientemente, y desde una óptica más cualitativa que cuantitativa, Harvey (2001) revisó la solución espacial de von Thünen considerando las diferencias entre productores y trabajadores, la relación entre clases sociales, los salarios, la moral y otras nociones. La lectura de este autor ofrece nuevas dimensiones de la obra de von Thünen muy poco consideradas hasta ahora por la economía cuantitativa.3
Este escrito aborda la teoría de von Thünen desde una perspectiva cuantitativa y dinámica. Con ello afronta una de las limitaciones del escrito de von Thünen (1826): la perspectiva estacionaria.
Puesto que superar una perspectiva estacionaria con un modelo dinámico no es tarea fácil y sólo puede cumplirse progresivamente, el objetivo de este escrito es extender el modelo estacionario de von Thünen planteando un modelo dinámico simple y resoluble mediante simulaciones numéricas simples, que entregue como primer resultado la evolución del ordenamiento espacial de una economía descentralizada en un escenario básico, donde las rentabilidades u son relativas y dependen, no sólo de las productividades r, de los precios p, de los costos de producción c y de los costos de transporte C · x, sino también de la tasa de interés del dinero (i) y del dinero implícito en el precio del terreno (pT), según:
El escenario dispone, además, que la tasa C varía de manera exógena y abrupta, mientras el precio pT del terreno varía de manera endógena y paulatina, movido por la rentabilidad u relativa.
Las disposiciones, ajenas a von Thünen (1826), podrían servir para afrontar, a posteriori, la otra limitación del escrito de aquel autor: su desconsideración del surgimiento endógeno de la ciudad junto con el uso del territorio. Pero, el escrito actual sólo intenta avanzar explorando algunos escenarios un poco más complejos que el primero: uno donde también varían las productividades; otro donde también varían los precios de los productos -pero no las productividades-; y otro donde existen dos ciudades, en lugar de una -pero no varían las productividades ni los precios.
Las operaciones matemáticas involucradas en el modelo dinámico actual y en su simulación numérica son bastante conocidas. La más sofisticada es la integración temporal, pero en las simulaciones es aproximada según Euler, mediante dos o tres de las cuatro operaciones escolares.
Una conclusión incómoda a la que conducen las simulaciones del modelo actual es la aparición de rentabilidades relativas negativas; vale decir, de terrenos “perdedores”, donde la rentabilidad bruta r (p - c - C x) de la producción es menor que el interés i pT del dinero implícito en el precio del terreno. Ciertamente, esa conclusión insinúa un problema macroeconómico, algo acerca del surgimiento de la ciudad, y la conveniencia de una investigación económica mayor, que incluya, al menos, relaciones entre el interés del dinero y el reordenamiento espacial. Otra conclusión a la que conducen las simulaciones del modelo actual y luego sus gemelas del modelo de von Thünen, es que el de von Thünen (1826) es poco estable ante las variaciones. Esto también insinúa la conveniencia de una investigación futura mayor. La sección I de este escrito presenta el modelo, sus escenarios y su desempeño; y la sección II clausura las conclusiones.
I. El modelo
Como fue dicho, muestro modelo es una versión extendida del modelo de von Thünen (1826) con varios escenarios. Concordamos con von Thünen en todos ellos, suponiendo simplistamente que los terrenos del territorio son muchos y continuos. Sin embargo, nos referimos a rentabilidades relativas, con descuento del interés del dinero implícito en el precio del terreno respectivo, como más realistas que las de von Thünen. Además, en todos los escenarios consideramos que el precio del terreno varía endógena y paulatinamente, movido por las rentabilidades en una realimentación ajena a dicho autor: los aumentos de las rentabilidades relativas causan un aumento del precio del terreno, que causa un aumento del interés del dinero implícito en tal precio, que causa disminuciones de las rentabilidades relativas. Adicionalmente, suponemos en todos los escenarios que la tasa de transporte disminuye exógena y abruptamente, replicando una propensión actual insólita para von Thünen. E incluimos variaciones circunstanciales en los escenarios: en uno, variaciones de las productividades; en otro, variaciones de precios de los productos; y en otro, coexistencia de dos centros de consumo que compiten entre sí para ser abastecidos por los productores.
I.1. Escenario básico: Inclusión de costo variable del terreno y de tasa variable de transporte
Imaginemos un centro de consumo único (una ciudad), centros de producción múltiples (terrenos) distanciados del centro de consumo contiguamente a lo largo de un territorio (un valle, aislado de lo demás), y productos de al menos tres especies posibles (verduras, frutas y cereales, por ejemplo) producidos (cultivados) en cada uno de los centros de producción.
Imaginemos también que interesa predecir, primordialmente, la evolución de la rentabilidad de la producción en cada terreno.
Consecuentemente, digamos que x es la distancia entre un centro de producción (terreno) y el centro de consumo (ciudad), medida en [km]; y t es el tiempo transcurrido, medido en [semana].
u es la rentabilidad de la producción en un terreno, (medida) en [U$ semana-1 km-2].
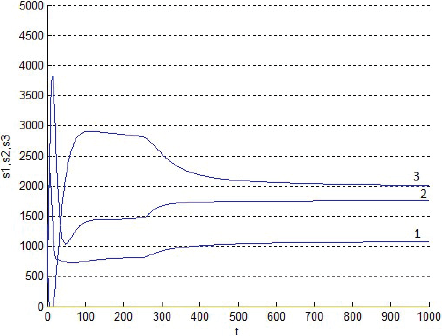
un es la rentabilidad de producir el producto de la especie n (para n = 1, n = 2 o n = 3, como si fuese el único producido), (medida) en [U$ semana-1 km-2]; sT,n es la fracción del terreno dedicada efectivamente a ese producto, en [km2 km-2].
rn es la productividad para el producto de la especie n, en [tonelada semana-1 km-2]; pn es el precio de ese producto, en [U$ tonelada-1]; cn es su costo (incluyendo insumos y salarios), en [U$ tonelada-1]; Cn es su tasa de transporte (incluyendo daños), en [U$ tonelada-1 km-1]; i es la tasa de interés del dinero, en [U$ U$-1 semana-1]; pT es el precio del terreno, en [U$ km-2]; qT,m,n es la intensidad con que el terreno pasa de la producción del producto de la especie m a la del producto de la especie n en [km2 semana-1 km-2].
CT,1 es la tasa de variación del precio del terreno, en [U$ km-2]; CT,2 es la tasa de traspaso de la producción de unos productos a otros, en [-].
Para atender adicionalmente a la oferta de productos en el centro de consumo, se puede añadir qn,o como el flujo del producto de la especie n ofrecido a la ciudad por la totalidad de los productores, en [tonelada semana-1].
donde a es el ancho del territorio, en [km].
Los datos siguientes, por ejemplo, completan lo necesario para hacer la simulación:
I.1.1. Dinámica
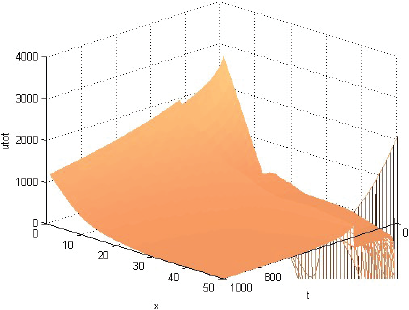
Claramente, las ecuaciones (1)-(7) es un sistema de ecuaciones no-lineal, resoluble mediante una simulación numérica bastante simple. Usando en ella la aproximación de Euler con paso temporal dt = 1 hacia el futuro para las integrales temporales de (3) y (5), y con paso espacial dx = 1 para la integral espacial de (7), se obtiene los gráficos de las Figuras 1-8.8
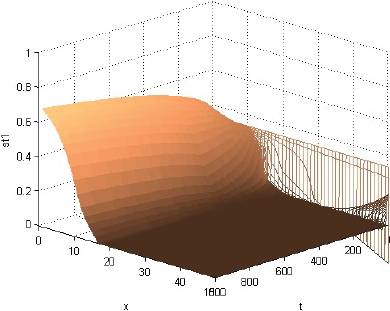
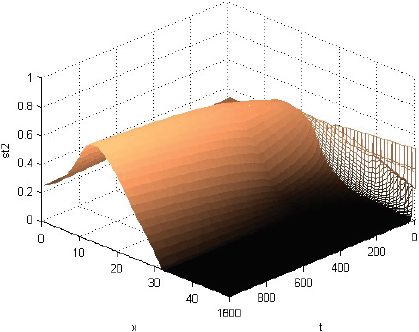
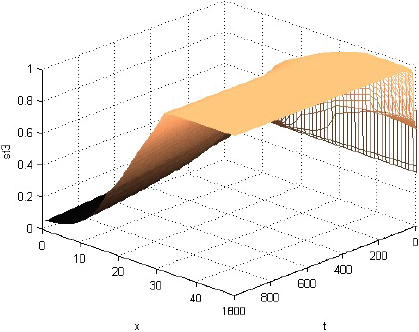
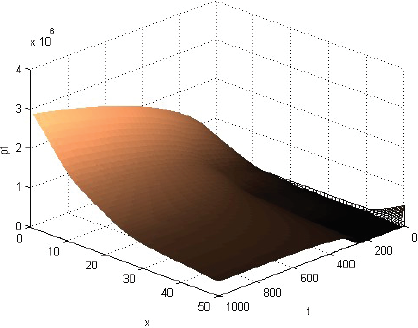
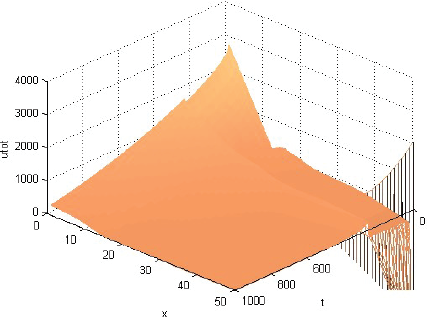
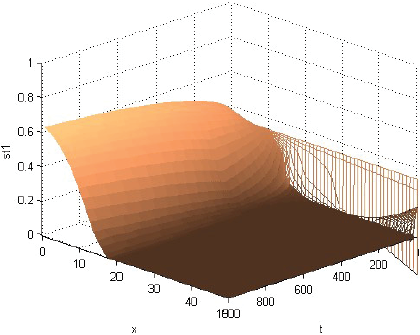
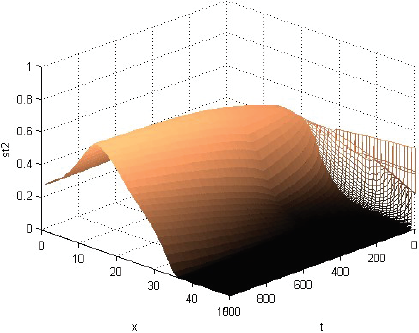
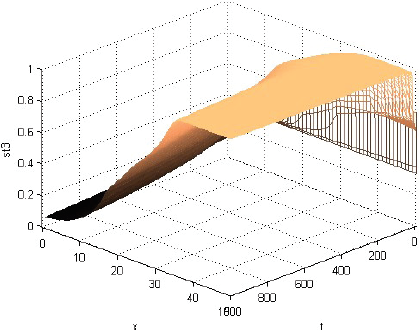
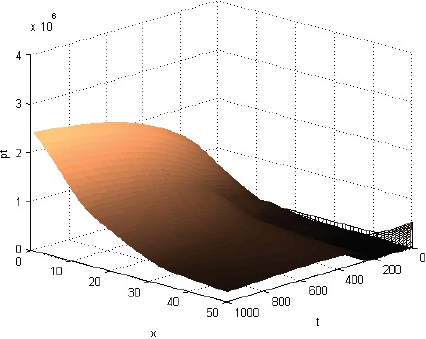
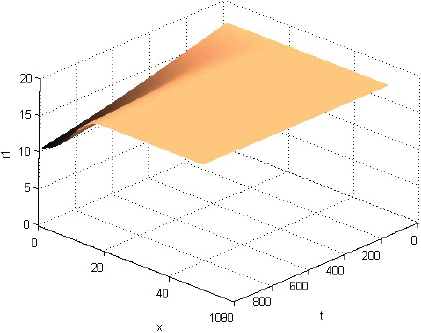
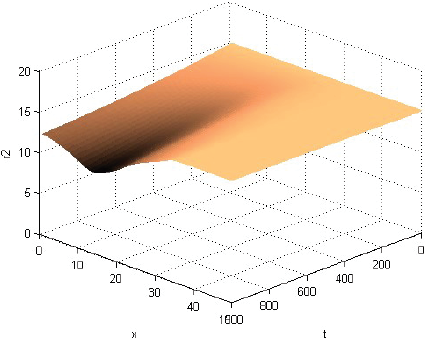
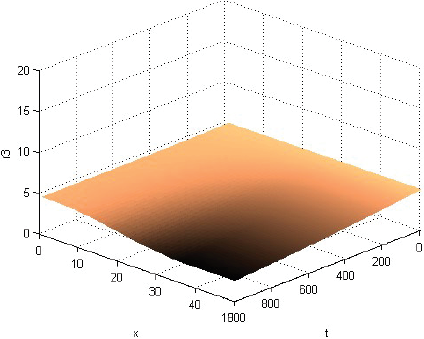
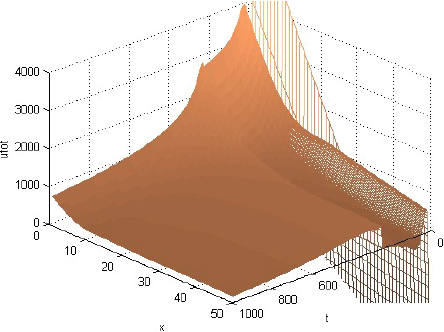
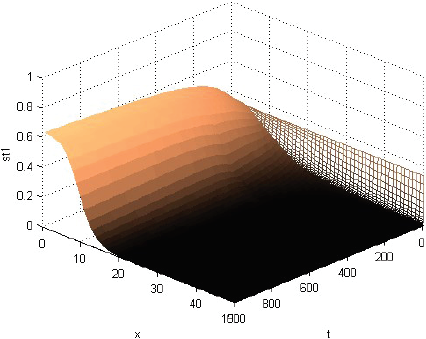
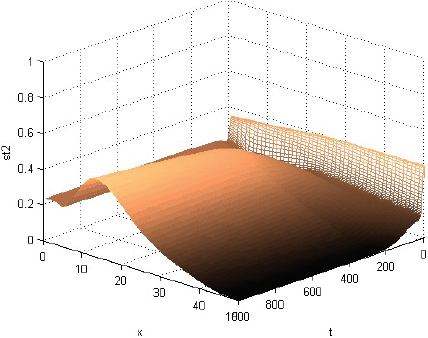
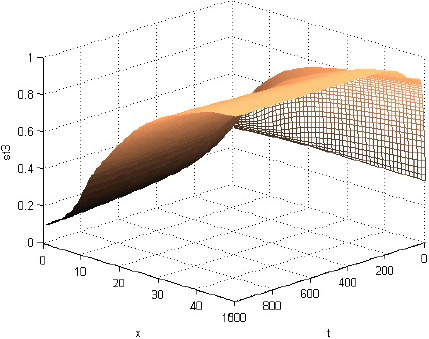
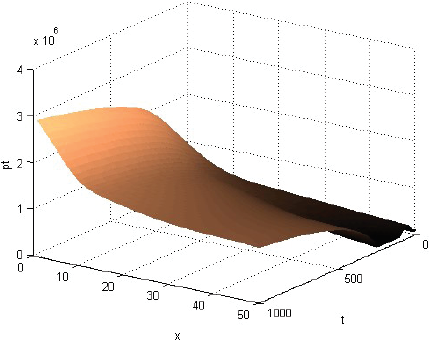
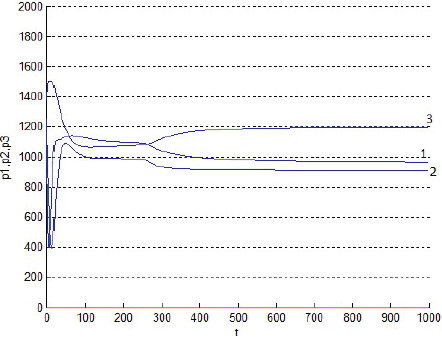
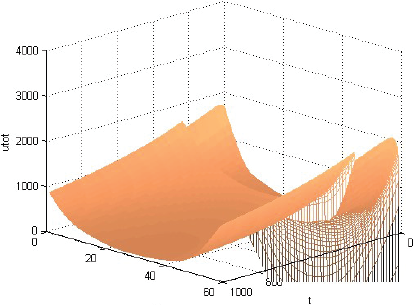
La Figura 1 muestra que la rentabilidad u de la producción evoluciona decayendo, pero manteniéndose casi en cualquier momento como alta cerca del centro del consumo y tendiente a cero lejos de él. La Figura 2 muestra que la fracción sT,1 del terreno, dedicada el producto 1, evoluciona afianzándose como alta cerca del centro de consumo y tendiente a cero lejos de él. La Figura 3 muestra que la fracción sT,2, dedicada al producto 2, evoluciona afianzándose como baja cerca del centro de consumo, alta en una posición algo alejada de ese centro y tendiente a cero lejos de él. La Figura 4 muestra que la fracción sT,3 evoluciona afianzándose como baja cerca del centro de consumo y alta lejos de él. Cabe destacar que las Figuras 2-4 también muestran que las fracciones sT,n no se igualan del todo a 1 ni a 0 con la distancia x. Económicamente, se puede justificar eso diciendo que así los productores pueden moderar los imprevistos del modelo, o satisfacer el consumo local. La Figura 5 muestra que el precio pT del terreno evoluciona creciendo, y manteniéndose casi en cualquier momento como alto cerca del centro de consumo y tendiente hacia el precio mínimo lejos de él. Y las Figuras 1-5, miradas atentamente, dejan entrever los efectos de las disminuciones exógenas y abruptamente discontinuas cuando t = 250, de las tasas de transporte CT .
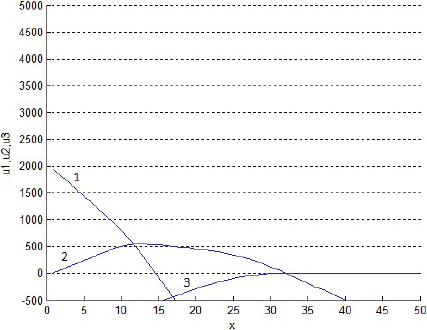
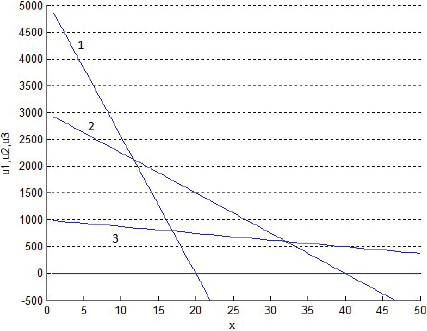
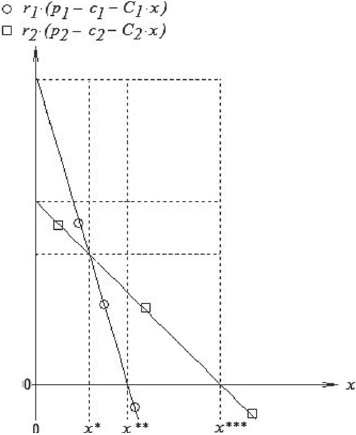
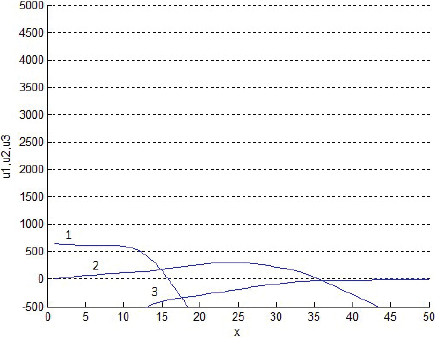
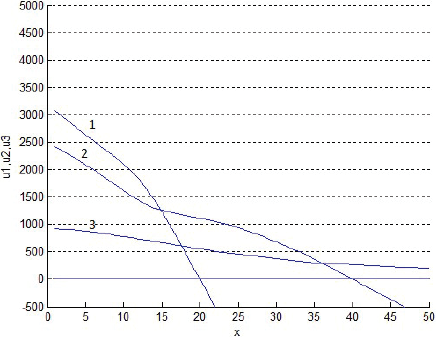
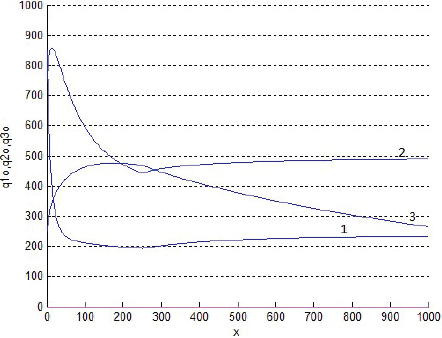
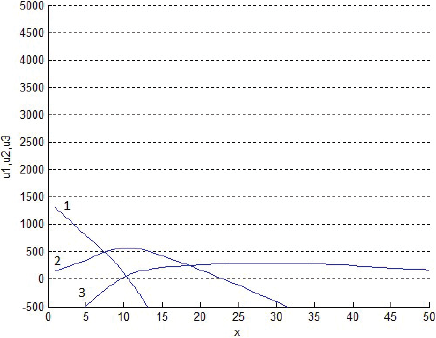
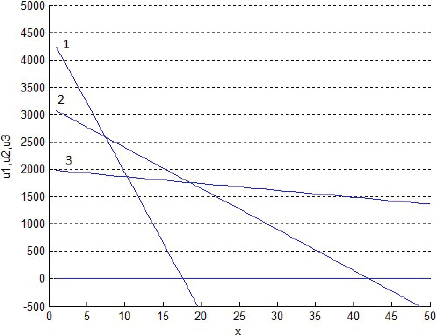
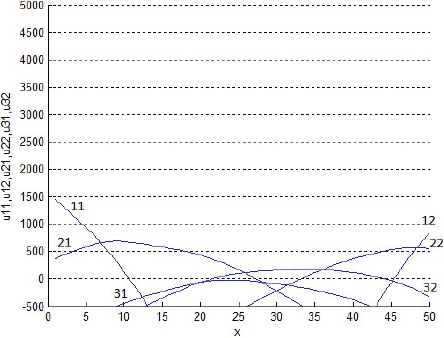
La Figura 6 superpone tres cortes transversales de los gráficos anteriores, de manera que muestra las rentabilidades un de los tres productos al cabo de 999 semanas de evoluciones. Después, las rentabilidades un tienden paulatinamente a hacerse negativas, aunque las figuras actuales no lo muestren. La Figura 7 grafica las rentabilidades según von Thünen (sin descuento del interés del dinero implícito en el precio del terreno). Al comparar ambas figuras, es oportuno recordar que, según von Thünen, en x se debe producir exclusivamente los productos de la especie cuya rentabilidad es ahí la máxima entre las de todos los productos potenciales. Así, a primera vista, la Figura 7 exige producir sólo el producto 1 si 0 < x < 12, el 2 si 12 < x < 32 o el 3 si 32 < x. Y si fuese por von Thünen, la Figura 6 exigiría lo mismo; sin embargo, según las Figuras 2-4, las fracciones sT,n no se igualan del todo a 1 ni a 0 con la distancia x: discrepan… suavizándose.
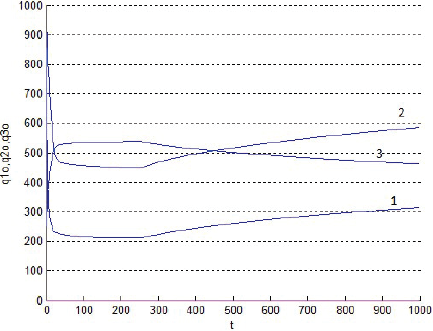
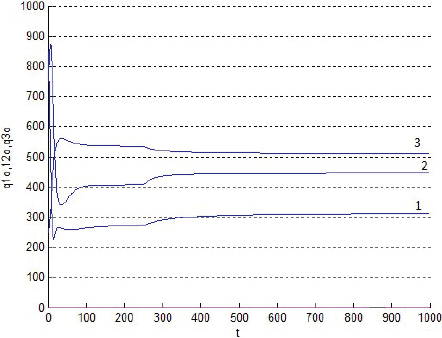
La Figura 8 muestra los flujos qn,o de los productos ofrecidos por la totalidad de los productores a los consumidores de la ciudad, lo cual invita a diversificar la atención puesta hasta ahora, preferentemente, en los terrenos.
I.1.2. Condiciones para el estado estacionario
Las evoluciones son promovidas por las integraciones expuestas en las ecuaciones anteriores, y allí están las claves con que dichas evoluciones cesan; esto es, las condiciones para el estado estacionario, que son inmediatamente cuatro:
Considerando la cuarta condición, suponiendo CT,1 ≠ 0 y pT (x) ≠ 0, y maniobrando algebraicamente muy poco; y considerando las tres primeras condiciones, insertando (6), resolviendo (para todos los casos en que 0 ≤ qT,m,n (x)), insertando (1) y la ecuación resultante de lo anterior, y maniobrando otro poco:
Considerando lo último, insertando (2), suponiendo i ≠ 0, y maniobrando:
Finalmente:
I.2. Escenario 1: Inclusión circunstancial de productividades variables, por deterioro
Imaginemos ahora que las productividades para los productos varían, dependiendo del deterioro de la calidad de la tierra a medida que se la usa para producirlos.
Imaginemos también lo demás del escenario básico.
Aunque se repiten (1)-(7), ahora los datos para las productividades rn cambian:
Rn es la productividad sin deterioro para el producto de la especie n, en [tonelada semana-1 km-2]; dn es el deterioro de la productividad para el producto de la especie n, en [-]:
T n es un coeficiente de deterioro, en [semana]9
Los datos siguientes, por ejemplo, completan lo necesario para hacer la simulación:
I.2.1. Dinámica10
Usando la aproximación de Euler con dt = 1 para las integrales temporales y dx= 1 para la espacial, se obtiene los gráficos de las Figuras 9-18 mostrados en el Apéndice 2.
En lo grueso, la rentabilidad u de la producción, las fracciones sT,n del terreno dedicadas a los diversos productos, y el precio pT del terreno, repiten los patrones dinámicos del escenario básico. En lo fino, dejan entrever los efectos de las disminuciones exógenas y abruptas (cuando t = 250) de las tasas de transporte CT .
Los flujos qn,o de los productos ofrecidos por los productores ya no tienden a estacionarse invulnerablemente como en el escenario básico; ellos tienden a variar afectados por los deterioros esperables del uso de la tierra según las fracciones sT,n (dos ascendiendo a costa del tercero, que decae). Los patrones de las productividades rn son, obviamente, dinámicos y no estacionarios como los de aquel otro escenario sin deterioros.
I.3. Escenario 2: Inclusión circunstancial de precios variables de los productos, por oferta y demanda
Imaginemos ahora que los precios de los productos dependen de sus existencias en el centro de consumo, y éstas dependen tanto de los flujos ofrecidos por los productores (sin productividades variables) como de los flujos demandados por los consumidores.
Imaginemos también lo demás del escenario básico.
Aunque se repiten (1)-(7), ahora los datos para los precios pn cambian:
Pn,1 es un coeficiente para el precio del producto de la especie n, en [U$ tonelada-1]; Pn,2 es otro coeficiente para el precio de ese producto, en [U$ tonelada-2]; sn es su existencia (o inventario) en el centro de consumo, en [tonelada]:
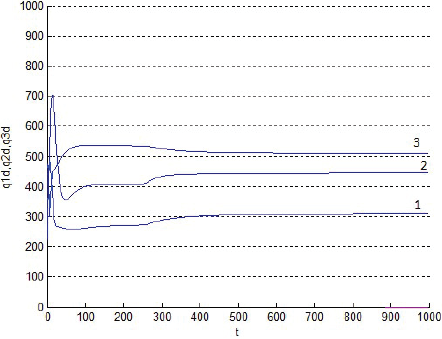
qn,d es el flujo del producto de la especie n demandado en la ciudad por la totalidad de los consumidores, en [tonelada semana-1]:
Qn,1 es un coeficiente de la demanda del producto de la especie n, en [tonelada semana-1]; Qn,2 es otro coeficiente de esa demanda, en [tonelada2 semana-1 U$-1].
Los datos siguientes, por ejemplo, completan lo necesario para una simulación:
I.3.1. Dinámica
Usando la aproximación de Euler con dt = 1 para las integrales temporales y dx = 1 para la espacial, se obtiene los gráficos de las Figuras 20-30 del Apéndice 2.
En lo grueso, la rentabilidad u, las fracciones sT,n y el precio pT repiten patrones dinámicos parecidos a los del escenario básico. En lo fino, se dejan entrever los efectos de las disminuciones exógenas y abruptas de las tasas de transporte CT . Los flujos qn,o de los productos ofrecidos por los productores, supuestamente liberados de los deterioros, tienden a estacionarse aparentando invulnerabilidad, como en el escenario básico. Los flujos qn,d de los productos demandados por los consumidores también tienden a estacionarse, y lo hacen buscando coincidir con los flujos qn,o de los productos ofrecidos, endógenamente.
Las existencias sn de los productos y sus precios pn se ajustan endógenamente.
I.3.2. Condiciones para el estado estacionario
A partir de las ecuaciones anteriores, las condiciones para el estado estacionario ahora son siete:
Maniobrando algebraicamente, esas condiciones se traducen en:
I.4. Escenario 3: Dos centros de consumo
Imaginemos ahora dos centros de consumo (dos ciudades, sin vaivenes de oferta y demanda) en ambos extremos de un territorio (un valle, aislado de lo demás), centros de producción múltiples (terrenos, sin deterioro de productividad) distanciados contiguamente a lo largo del territorio, y productos de varias especies posibles en cada uno de los centros de producción, con una taxonomía doble: tanto por naturaleza (verduras, frutas o cereales) como por destino (una ciudad u otra), de manera que las especies resulten seis, en número, por multiplicación (verduras para la primera ciudad, verduras para la segunda, frutas para la primera, frutas para la segunda, cereales para la primera o cereales para la segunda).
Imaginemos también que interesa predecir, primordialmente, la evolución de la rentabilidad de la producción en cada terreno.
Consecuentemente, digamos que x es la distancia entre un centro de producción (terreno) y uno de los centros de consumo (una de las ciudades), en [km]; y t es el tiempo transcurrido, en [semana].
u es la rentabilidad de la producción en un terreno, en [U$ semana-1 km-2].
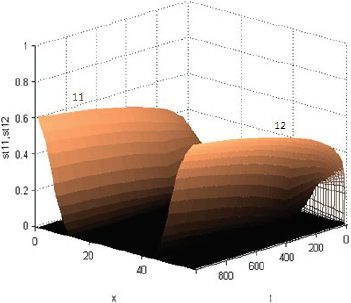
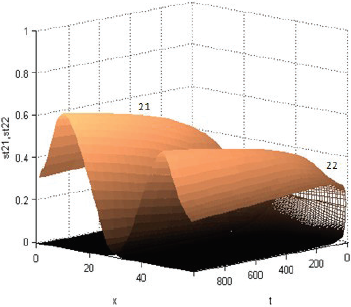
un es la rentabilidad de producir el producto de la especie n (para n = 11, n = 12, n = 21, n = 22, n = 31 o n = 32, como si fuese el único producido), en [U$ semana-1 km-2]; y sT,n es la fracción del terreno dedicada efectivamente a ese producto, en [km2 km-2]:
rn es la productividad para el producto de la especie n, en [tonelada semana-1 km-2]; pn es el precio de ese producto, en [U$ tonelada-1]; cn es su costo (incluyendo insumos y salarios), en [U$ tonelada-1]; Cn es su tasa de transporte, en [U$ tonelada-1 km-1]; xn es la distancia entre un centro de producción y el de consumo correspondiente, en [km]; i es la tasa de interés del dinero, en [U$ U$-1 semana-1]; pT es el precio del terreno, en [U$ km-2]; y qT,m,n es la intensidad con que el terreno pasa de la producción del producto de la especie m a la del producto de la especie n, en [km2 semana-1].
Los datos siguientes, por ejemplo, completan lo necesario para hacer la simulación:
I.4.1. Dinámica
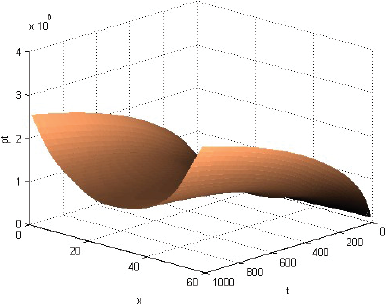
Usando la aproximación de Euler con dt = 1 para las integrales temporales, se obtiene los gráficos de las Figuras 31-37 del Apéndice 2
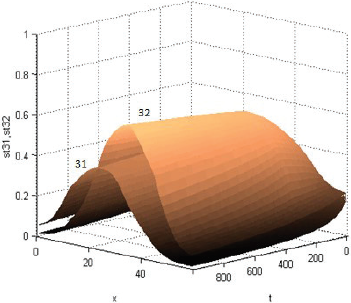
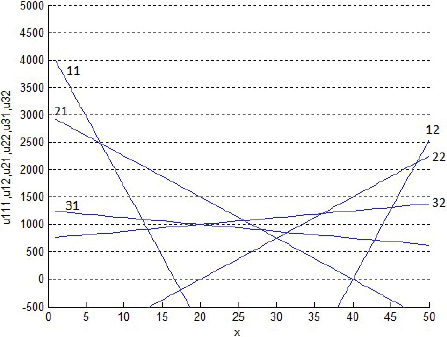
La presencia de dos centros de consumo no modifica mayormente los patrones dinámicos del escenario básico. Sólo expande las opciones del comercio involucrado. Anecdóticamente, en línea con lo pensado por von Thünen, las Figuras 36 y 37 mostradas en el Anexo 2 exigirían que los productos de la especie 31 (cereales para la ciudad 1) no se produzcan.
Conclusiones
En este escrito hemos afrontado la limitación estacionaria de von Thünen (1826) que predice un patrón de anillos concéntricos de mono-cultivos con un gradiente espacial de rentas (máximas) en descenso monotónico desde las inmediaciones de una ciudad (un centro de consumo, x = 0) hasta un horizonte lejano. Tal gradiente puede explicarse sumariamente apelando a la Figura A.1 y los comentarios del Apéndice que expone esta exigencia primordial de dicho autor.
Es sabido que algunas culturas nativas de América Latina, muy anteriores a von Thünen (1826), ordenaron sus cultivos con un patrón de anillos circulares de forma similar a la solución del autor. Pero no parece saberse si acaso esas culturas ordenaron así sus cultivos urdiendo una maximización de rentas que decrecen hacia la periferia, como la solución de von Thünen sugiere.
Al dinamizar el modelo estático de von Thünen (1826), las rentas descendentes hacia la periferia que aparecen en su escrito también aparecen en el nuestro, aunque aquí evolucionando sin el mismo carácter monotónico. Sin embargo, los anillos de producciones únicas no aparecen en nuestras soluciones (o simulaciones).
En efecto, en nuestro modelo dinámico los productores buscan maximizar sus rentas sin ponerse a pensar en líneas rectas de figuras como las mostradas en el Apéndice A.1; a elegir las líneas de más arriba en los tramos pertinentes, y a producir exclusivamente los productos de las especies que corresponden a las líneas elegidas. Sin embargo, ellos no son irracionales: ensayan variaciones de producción menos complejas; toman en cuenta los efectos favorables o adversos que tienen esas variaciones en sus rentas, y vuelven a ensayar, repetidamente. Por supuesto, no pueden empatar prontamente las rentas de los agricultores de von Thünen si de pronto se dan condiciones acordes con las supuestas por él; y, como los agricultores presentes en su modelo, tampoco pueden “ganar” donde les toca “perder” con rentas negativas. Pero las condiciones actuales no son las de von Thünen, y las figuras actuales no son de líneas rectas.
Por un lado, entre las condiciones actuales hay rentabilidades relativas que dependen, no sólo de las productividades, de los precios de los productos, de los costos de producción y de los costos de transporte, sino también de la tasa de interés del dinero y de los dineros implícitos en los precios de los terrenos. Adicionalmente, los precios de los terrenos varían de manera endógena y paulatina, movidos por las rentabilidades, y las tasas de transporte varían de manera exógena y abrupta. Además, alternativamente, las productividades o los precios de los productos varían de manera endógena y paulatina, afectados por los deterioros de los terrenos o por las existencias de productos en el centro de consumo; y todavía, en vez de un centro de consumo puede haber dos.
Por el otro lado, las Figuras 6, 14, 25 y 36 sugieren que nuestra aproximación dinámica al problema de von Thünen (1826) no arroja líneas rectas y monotónicas como las de este autor, sino de líneas curvas cuyas cúspides no se ubican necesariamente en las inmediaciones de la ciudad: son líneas de rentabilidades con descuento por el interés de los dineros implícitos en los precios de los terrenos, que tienden a ser mayores cerca de x = 0.
Aún ante esas líneas curvas, nuestros productores podrían elegir la producción exclusiva de los productos que corresponden a las líneas de más arriba en los tramos pertinentes de las figuras; pero no lo hacen: van dosificando las producciones según fracciones que tienden a ser mayores para los productos correspondientes a las líneas de más arriba en dichas figuras, sin que sean nulas para otros productos. Eso se aprecia, por ejemplo, en las Figuras 2, 3 y 4, 10, 11 y 12, 21, 22 y 23, y 32, 33 y 34.
El modelo actual, con sus producciones inclusivas, titubea poco ante las variaciones de los escenarios; en cambio, el modelo de von Thünen, con sus producciones exclusivas tras haber sido resueltas mediante una perspectiva estacionaria se vuelve inestable: varias otras simulaciones numéricas no incluidas en este escrito muestran que el modelo estacionario de ese autor no es fácil de defender al introducir una visión dinámica. Analizar en profundidad este comportamiento es parte de nuestra actual agenda de investigación.
En el modelo actual, la aparición incómoda de terrenos “perdedores”, con rentabilidades brutas menores que el interés del dinero implícito en los precios de los terrenos insinúa un problema macroeconómico o de economía política y hace pertinente una investigación futura mayor que incluya, al menos, relaciones entre el interés del dinero y el re-ordenamiento espacial, y algo acerca del surgimiento de ciudades. Ahora sólo parece caber un comentario breve y quizás simplista al respecto: las rentabilidades aludidas son de las producciones; los terrenos “perdedores” podrían dedicarse a otras actividades económicas (por ejemplo, turísticas; o inmobiliarias, con la consiguiente siembra de ciudades); y/o podrían ser compensados mediante subsidios, si las demandas de los productos son agobiantes en las ciudades.
Considerar que las rentabilidades dependen (también) de los dineros implícitos en los precios de los terrenos, y que éstos varían movidos por las rentabilidades, podría servir para afrontar, a posteriori, la otra limitación del escrito de von Thünen: su desconsideración del surgimiento endógeno de la ciudad, junto con el uso del territorio. Esto también forma parte de nuestra actual agenda de investigación. Finalmente, otra línea de investigación futura tiene el ambicioso, pero desafiante objetivo, de introducir progresivamente en nuestro modelo algunas de las ideas de Harvey (2001); el concepto de conflicto entre productores y trabajadores aparece por ahora en nuestro horizonte cercano.











 nova página do texto(beta)
nova página do texto(beta)