Introduction
In mathematics or mathematical chemistry courses, the concepts of algebra are traditionally transmitted from “experts” to students in a unidirectional way. This methodology follows a learning route; it focuses attention on the content and the teacher instead of students. They learn, store and use the information to solve problems given in a book. This process facilitates the procedural learning. Consequently, they underlook the concepts of abstract and linear algebra by considering it useless. The problem-based learning, PBL, provides several ways to overcome the above mentioned drawbacks. PBL offers a model where students solve a problem with clear learning purposes. In this approach, the teacher plays a key role in motivating students to learn in an active and cooperative learning environment. PBL allows the understanding of complex concepts because the reflective observation and abstract conceptualization are the cause - and consequence - of the concrete experience and the active experimentation, as established by the Kolb’s learning cycle (Kolb & Kolb, 2012). Additionally, it is possible to integrate the knowledge of several disciplines depending on the nature of the problem (Ashraf, Marzouk, Shehadi, & Murphy, 2011; Cowden & Santiago, 2016). There are many successful examples using PBL in chemistry, mainly in laboratories (Fakayode, King, Yakubu, Mohammed, & Pollard, 2012; Llorens-Molina, 2010) and courses with experimental applications (Hopkins & Samide, 2013; Jansson, Söderström, Andersson, & Nording, 2015). However, the application of PBL for contents with a conceptual orientation is scarce in the literature (Gurses, Dogar, & Geyik, 2015).
The effectiveness of PBL in teaching mathematics (Ajai, Imoko, & Emmanuel, 2013; Ali, Hukamdad, Akhter, & Khan, 2010) and physics (Sahin, 2010) has been demonstrated. An example was given by Chen connecting the structure of Luce chapel (Thungai University, Taiwan) with geometry (Chen, 2013). Based on these ideas, we have designed an exercise of PBL allowing the integration of abstract and linear algebra concepts with chemistry using elements of graph theory, matrices, and vector spaces.
In literature, the structure - property relationships has been a typical example of the application of graph theory and matrices (Mihalić & Trinajstić, 1992; Murphy, 2007; Ram, 1999). Bearing in mind this idea, we then broaden the knowledge range by including the concepts of vector space, vector algebra and, linear, quadratic and bilinear forms through a chemical application in a PBL environment. In this sense, the TOMOCOMD (acronym for TOpological Molecular COMputational Design) approach represented a tool to assess the learning of the before mentioned concepts. Marrero-Ponce defined these molecular descriptors taking fundamental principles of linear algebra and graph theory, which were useful to promoting conceptual learning (Marrero-Ponce, 2003; Marrero-Ponce, Garit, Torrens, Zaldivar, & Castro, 2004; Marrero Ponce, 2004).
The Problem
The starting point of the PBL exercise is the problem proposal (Ram, 1999). The goal of selecting a problem is motivating students to take an active part in their learning. In this work, the proposed problem is addressed to course of mathematical chemistry or algebra where only chemistry students assist. There are universities where algebra courses consist of students from several disciplines (chemistry, physics, mathematics, and engineering) and mathematicians teach these courses. Students with other learning interest will not be motivated, and consequently their performance decreased (Jones et al., 2013). In this scenario, problem-based learning fit by providing different problems according to the learning interest of the students, or allowing them to propose the problem.
The problem proposal initiates with a discussion in order to obtain diagnostics on prior knowledge and necessary skills. It is possible that students have different strength in prior knowledge. Several authors found an influence of the quality of prior knowledge on success rate and dropout (Bledsoe & Flick, 2012; Hailikari & Nevgi, 2010), but not in problem-solving skills (Bledsoe & Flick, 2012). Therefore, it is necessary to perform a diagnostic test to get a baseline as well as to plan and carry-out activities to strengthen it.
With the aim of start the discussion to choose the problem, we will look into physicochemical properties of organic compounds and their importance in industrial processes. Then, the discussion is oriented toward the empirical relation between a property value and chemical structure of compounds (Murphy, 2007). For instance, molar mass vs. density in hydrocarbons, basicity of the leaving group vs. reaction rate in nucleophilic substitution reactions, etc. Furthermore, the participants brainstorm and highlight the convenience of the numerical prediction of physicochemical properties to reduce costs and save time in industrial processes to gain additional insights. Here, the driving question enclosing the problem arrives from the discussion:
How can we predict the physicochemical properties of organic compounds from their structure?
From this point, the teacher guides the students to solve the problem. The students carefully select the property to predict - endpoint - and the set of molecules to be used. They form groups to study one pair of endpoint-molecules set. Finally, the methodology is divided into three steps: (1) Molecular representation (2) Information codification, and (3) Properties prediction.
Molecular representation
Humans represent the molecules as lines and letters, symbolizing bonds and atoms, respectively. Another set of symbols may identify lone pairs, delocalized electrons, chirality and other molecular characteristics. However, these symbols are not readable by COMputationals. The students should discuss the concepts of molecular representations to make it possible translating these humans structures to COMputational objects, e.g. coordinate matrix (M), internal coordinate matrix (Z), atom connectivity matrix (A), etc., (Todeschini & Consonni, 2009). Consequently, they identify matrix theory as a learning need, and research in this field starts.
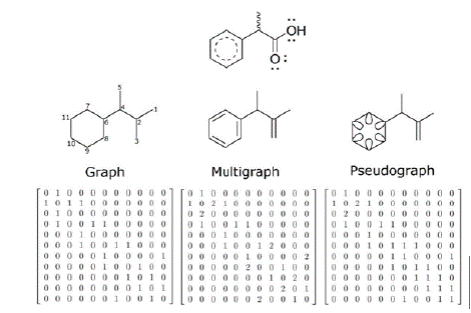
The chemical structures can be represented as matrices by using graph theory (Kerber, Laue, Meringer, Rücker, & Schymanski, 2014; Mihalić & Trinajstić, 1992). In algebra, a graph G is a finite set V of vertices and a set E of unordered pairs of the form (i,j) or (j,i) where i and j are in V, called the edges of G. In chemical graph theory, the atoms are associated to vertices and covalent bonds to edges (Kerber et al., 2014; Mihalić & Trinajstić, 1992; Todeschini & Consonni, 2009). An extension of this theory is achieved by increasing the edge multiplicity (multigraph) - i.e. increasing bond order (Todeschini & Consonni, 2009) - and/or adding loops (pseudograph) to codify aromaticity (Marrero-Ponce, 2003). All of these chemical objects are represented by a symmetric matrix A, known as adjacency matrix, where aij ≠ 0 if the vertices i and j are connected or, i = j have a loop, and aij = 0 otherwise. Figure 1 shows the process followed to obtain adjacency matrix from the molecular graphs, multigraph and pseudograph. Subsequently, students would follow this procedure to represent the molecules of their own dataset.
Information encoding
A definition of molecular descriptors involves a logical or mathematical procedure to obtain a number encoding the structural and chemical information (Todeschini & Consonni, 2009). Among the mathematical procedures to calculate descriptors, several definitions within matrix theory have shown to be useful, e.g. determinant (Graovac & Gutman, 1979), characteristic polynomial, first eigenvalue (Gutman & Vidovic, 2002). The discussion on these molecular descriptors allows the students and teacher to open a reflection space around matrix properties and the transferable knowledge in chemical applications. In other words, students will use the knowledge and how, why and when apply the vector and matrix theories to solve a real problem (Pelligrino & Hilton, 2012).
Moreover, a descriptor definition involving vector space concepts and theory possibly would help students to acquire conceptual knowledge and, increases the transferability. The TOMOCOMD approach has defined the molecular vector space, where molecular vectors contain the chemical information of atoms forming molecule (Gutman & Vidovic, 2002; Marrero-Ponce, 2003; Marrero-Ponce et al., 2007, 2004; Marrero Ponce, 2004). For more information, please see J. Cheminformatics, 2017, 9:35: https://doi.org/10.1186/s13321-017-0211-5, where the initial proposed algebraic formalisms for characterizing topological (2D) and chiral (2.5D) molecular features through atom- and bond-based ToMoCoMD-CARDD (acronym for Computer Aided Rational Drug Design) molecular descriptors were re-implemented as the QuBiLS-MAS (acronym for Quadratic, Bilinear and N-Linear mapS based on graph-theoretic electronic-density Matrices and Atomic weightingS) software (http://tomocomd.com/qubils-mas). Each vector component is an atomic property of each element present in the molecule. For example, the Mulliken’s electronegativity of the atom A, χA, take the values χH = 2.2 for Hydrogen, χC = 2.63 for Carbon, χN = 2.33 for Nitrogen, χO = 3.17 for Oxygen, χCl = 3.0 for Chlorine and so on. This approach allows us to express compounds such as benzene, cyclohexane, hexane and all the constitutional and geometric isomers of hexane through a general kind of vector χ = (χC;χC;χC;χC;χC;χC). On the other hand, n-propanol, iso-propanol, propanal, and acetone may be represented by (χC, χC, χC, χO) or any permutation of the components of this vector. In summary, the properties numerically characterizes each atom in the real set (
This scenario gives the possibility of introducing the knowledge about vector spaces. The groups should discuss about concept of basis set, linear transformations, and they will show the multiple applications. The success of this discussion will guarantee the easy translation of mathematical concepts into the chemical application by promoting critical thinking and the multiple representations (Cowden & Santiago, 2016; Lin, Son, & Rudd, 2016). Based on this, we have chosen the TOMOCOMD approach that proposes the adjacency matrix of pseudograph as a basis of molecular vector space. Additionally, it has defined the linear, quadratic and bilinear maps as molecular descriptors. Linear applications in the vector space, which in matrix notation become as:
where A is the pseudograph’s adjacency matrix, x and y are molecular vectors, whose components are the atomic properties x and y, respectively; and u is a vector with components are one, the t superscript means vector transpose. The conceptual goals are related to the analysis of vector space theory to assess the TOMOCOMD approach, and to compare with other applications of the vector space concepts, e.g. Hilbert space in quantum chemistry. The procedural aspects optionally can be managed by COMputational software as an alternative to hand calculations. COMputational algebra software, free [OCTAVE (Eaton, 2016), SAGEMATH (SageMath, 2016)] or commercial [MATLAB (MATLAB, 2016), MAPLE (Maplesoft, 2016)], are good choices to design the matrices, molecular vectors, and carry out the needed mathematical operations (Jansson et al., 2015). Figure 2 shows the workflow guiding the students through the calculation procedure of molecular descriptor.
Prediction of properties
According to the evaluation strategy, it is mandatory to include the prediction of physicochemical properties in order to show a complete work with a real-life application. The prediction of physicochemical properties usually involves finding a model by multiple linear regression of selected descriptors (Mihalić & Trinajstić, 1992). The groups select one endpoint - physicochemical property - and one molecular datasets from several given in books (Kerber et al., 2014) and scientific papers (Marrero-Ponce, 2003). Finally, the descriptors are calculated and used as the variables of the linear regression model. The ordinary least squares procedure can be performed by using software with multiple linear regression capability.
Evaluation of Learning
The evolution from the traditional scheme to PBL gave us a set of successful evaluation strategies as consequence of trial-and-error experience. The evaluation instrument design suggests an analysis of the expected learning outcomes (Gron, Bradley, McKenzie, Shinn, & Teague, 2013) - See Table 1. Written exams, group reports, portfolios and questionnaires are efficient instruments to evaluate specific learning outcomes, but they avoid the self- and co-evaluation. Our experience has shown that a strategy promoting all of these aspects is a “scientific congress”. The students should prepare an end-product - poster or oral presentation - of their research projects (Ashraf et al., 2011). This strategy results in a successful personal experience combined with a meaningful learning. The peers, classmates or public, evaluate the learners about the projects.
Table 1 Learning outcomes and evaluation instrument in the PBL exercise
| Learning Outcomes | Evaluationa |
|---|---|
| Procedural skills | |
| Write molecular vectors | WE, PF |
| Write adjacency matrix of graph, multigraph or pseudograph | -- |
| Use scientific software to design vector and adjacency matrix | II, PF |
| Use scientific software to perform matrix and vector operations | -- |
| Conceptual goals | |
| Understand vector as non-solely geometric entities | II, GI |
| Assess and justify the use of vectors to represent molecules | II, GI, OP |
| Understand vector space as an abstract mathematical object | -- |
| Identify the adjacency matrix as a molecular representation | -- |
| Interpret the adjacency matrix as a basis of molecular vector space | -- |
aWE: Written exam; PF: Portfolio; II: Individual interview; GI: Group interview; Oral o poster presentation.
A working example
One from authors implemented this pedagogical methodology in a Mathematical Chemistry course. The students were in the 5th semester (20 in-class hours/week, 1 in-class hour = 1 credit = 1 real hour) of their 10-semester undergraduate Chemistry program. This course has 4 in-class hours/week and 2 hours/week of tutorial session. The course structure includes three large learning contents: Vectors and Matrices (5 weeks); Group Theory and Symmetry (5 weeks); and Differential Equations (6 weeks). The Mathematical Chemistry course was created with the aim of providing the knowledge requirements for Inorganic Chemistry I and II, Physical Chemistry II and Quantum Chemistry. In this semester the students have the necessary knowledge of thermodynamical properties of matter (Physical Chemistry I), molecular structure (General Chemistry I and Organic Chemistry I) and they are capable to model molecules (Computational Chemistry).
The historical performance of the course is low, with high dropout (~ 45%) and failure (~ 18%) rates. According to interviews, the students leave the course due to the perceived lack of applicability in chemistry. The students thought that the knowledge is necessary for deducing equations of the other courses. This general apathy could be the cause of the course failure in some students. This reason led us to change the learning strategy.
The new methodology was applied during the first 5 weeks, matrices and vectors, in a 49-students course and the results compared with the group of previous semester --- 27 students, 40.7% dropout and 25.9% failure rates. The prediction of the physicochemical properties of the 18 octane isomers published in Molecular Descriptors web page was the molecular database for the vectors and matrices. The 49 students were divided into 9 groups of 5 students and 1 group of 4 students. Each group was assigned a property of the Table 2.
Table 2 Properties of the 18 octane isomers
| Group | Properties |
|---|---|
| 1 | boiling point (BP) |
| 2 | melting point (MP) |
| 3 | heat capacity at T constant (CT) |
| 4 | Entropy (S) |
| 5 | density (DENS) |
| 6 | enthalpy of vaporization (HVAP) |
| 7 | enthalpy of formation (HFORM) |
| 8 | molar refraction (MR) |
| 9 | total surface area (TSA) |
| 10 | octanol-water partition coefficient (LogP) |
A schedule tracking the progress in student’s activities based on the learning purposes (See Table 3) was established. Several group interviews were carried out weekly, and the advances and delays were collected in the schedule form. At this time the groups with difficulties (1, 2, 4 and 10) were guided to a satisfactory solution of their problems. The main reason of delays were solved with the codification of local fragments (Marrero Ponce, 2004) after a discussion within the group.
Tabla 3 Chronogram of activities
| Time | Activity |
|---|---|
| Week 1 | Collection of atomic properties and modelling the structures |
| Week 2 | Building molecular vectors, adjacency matrix and descriptors |
| Week 3 | Modelling properties with calculated descriptors |
| Week 4 | Discussion of results |
| Week 5 | Oral Presentation |
The experimental properties were poorly predicted by the total TOMOCOMD approach following the workflow described in Figure 2. The data around prediction line showed high dispersion, revealing a lack of information encoding of the total descriptors for the properties 1, 2, 4 and 10 of Table 2. The feedback with the teacher promoted deeper researching on the theme. The students were able to select between a new descriptor family and calculating local descriptors under TOMOCOMD approach. The local approach was included and a better prediction of properties was obtained. The TOMOCOMD approach (Marrero-Ponce et al., 2004; Marrero Ponce, 2004) defines the local information matrix for a fragment L [A(L)] as the Hadamard product of the structural information matrix (adjacency matrix, A) and a fragment information matrix (F) calculated by:
In relation to learning purposes, the students learned and applied the Hadamard matrix product as an alternative for the product of two matrices.
The evaluation was performed in two scenarios: (a) in-class and (b) the problem. The former corresponds to the knowledge managed in-class hours and it evaluated the cognitive and procedural competences related to the contents of the course. The instruments were 2 (20 min) in-class tutorials (vector and matrices) and one 60-min written exam (vector and matrices).
In the problem scenario, it was evaluated the competences addressed to the transfer of knowledge to solve a real problem. This evaluation was performed weekly, with the interviews to the students where a series of questions involving learning outcomes were made. In the Week 1 and 2 were evaluated the conceptual goals, while procedural skills were inquired in the week 3 and 4. The oral presentation was evaluated by peers (classmates) and teacher. Figure 3 and 4 show the translated forms of evaluation filled by students and the teacher. The procedural skill and conceptual goals were included as item in the evaluation.
Finally, the application of PBL through the strategy proposed in this work reduced the repetition rate to 0%, while the drop-out rate slightly reduced to 32%. The overall pass rate has increased to 68% and the performance rate significantly increased from 10.10 ± 1.61 to 12.75 ± 2.31 points in a 20 points basis --- paired t-test: t(74)= 5.2879, p<0.0001. These results showed an increase of the student engagement to the problem solution, decreasing the dropout-rate. The cause of the residual drop-out was the resistance-to-change, as expressed by an interview with dropped students. This fact guaranteed an internalization of mathematical ideas related to the problem (Ross & Willson, 2012). The decreasing on the repetition rate is a consequence of the student engagement, and the conceptual understanding. The latter is evidenced by the results of the different evaluation instruments where conceptual, procedural and critical thinking outcomes were observed and qualified.
Future Outlook
The learning strategy presented in this report attempts to reduce the widening knowledge gap between linear algebra and problem solving in cheminformatics and quantum chemistry. First, the concept of vector space through an alternative representation as presented in this work allows the scaffolding of knowledge from the simple to complex concepts, i.e. Hilbert Space in Quantum Chemistry. On the other hand, it revealed the direct application in chemistry of formally unknown mathematical elements, such as graph theory. Students with special aptitudes for mathematics will be motivated in research in mathematical chemistry, cheminformatics, chemometrics, and computational chemistry. Likewise, teachers will be motivated to offer courses deepening the knowledge in the before mentioned areas. The solid previous knowledge of mathematical chemistry course will encourage student to develop research activities.
The flexibility of PBL allows test several evaluation strategies. In this work we have carried-out a “scientific congress” for evaluating the knowledge in this PBL exercise. However, teachers may consider this evaluation inadequate depending on the nature of the course, i.e. career advance, previous knowledge, learning outcomes, nature of the group. A special consideration should be taken with the conceptual goals and activities to evaluate it. These contributions help the approach to improve the learning process of mathematical concepts.
Concluding remarks
This work reported the development of a problem-based learning strategy integrating mathematical concepts of linear and abstract algebra in undergraduate chemistry students. The proposed experience increased the conceptual understanding of mathematics involved in the TOMOCOMD molecular descriptors. The use of COMputational algebra software helped students save time of hand calculation, and prioritizing the student-student and student-tutor discussion on concepts and definitions. Our own experience demonstrated an enhanced student learning in comparison to the traditional model of teaching linear algebra or mathematical chemistry. The evaluation generated positive responses of students to cooperative work, and enhancing the self- and co-evaluation. Finally, this strategy improved the overall pass and success rate.











 nueva página del texto (beta)
nueva página del texto (beta)