1. Introduction
The hypothesis of purchasing power parity (henceforth PPP) posits that any set of bundles comprised by tradeable goods -and quoted in the same currency- should have the same price everywhere (Officer, 1976; Rogoff, 1996; Obstfeld and Rogoff, 1996; Taylor and Taylor, 2004; Taylor, 2006; Lothian and Taylor, 2008; Shaikh, 2016). Thereby, the so-called law of one price (henceforth LoP) operates not only strictly within national borders but also among countries. Although the origin of this theory -or doctrine- is rooted likely in the works by Azpilcueta, a prominent scholar of the Salamanca school in XVI century, as noted by Humphrey (1979), Thornton was the first author who clearly enunciated the mechanism on which the PPP hypothesis rests. In his work entitled An Enquiry into the Nature and Effects of the Paper Credit of Great Britain, Thornton stated that an increase in prices in those countries with an overabundance of paper money in circulation would provoke an equivalent rise in the nominal exchange rate (Humphrey, 1979).
Nevertheless, Humphrey (1979) highlights that Wheatley enunciated for the first time the absolute version of the PPP hypothesis. According to Wheatley, the course of the nominal exchange rate is solely governed by the relative prices which are, in turn, determined by the amount of money in circulation in each country. In such a framework, hence, the PPP hypothesis was conceived as an extension of the quantity theory of money, put forth by Hume, to the international market (Frenkel, 1978).
It is worth mentioning that the PPP hypothesis’ version enunciated by Wheatley should be considered as the extremist version because it refuses the influence of actual shocks on the exchange rates. In other words, Wheatley sustained that the movements of exchange rates are purely a monetary phenomenon (Humphrey, 1979).
Like Wheatley’s, Ricardo’s (1821) version of the PPP hypothesis is based on the quantity theory of money. Ricardo contended that the nominal exchange rate would be always at the equilibrium setting thanks to relative money stocks, which compelled the abandonment of the theory of natural price to analyze the mechanisms ruling international prices1. It should be emphasized that the influence of Ricardo’s oeuvre was crucial for bringing the PPP theory to the category of a fundamental law of economics.
The first empirical attempt to test the PPP hypothesis correspond to Cassel (Frenkel, 1978; Humphrey, 1979; Rogoff, 1996; Taylor and Taylor, 2004). Cassel’s contributions (1918, 1916) to the PPP doctrine are remarkable. He was the first author to coin the term purchasing power parity. Secondly, he established the difference between the absolute version and the relative version of the PPP hypothesis. Thirdly, he proposed using both cumulative price indices (CPI) and whole price indices (WPI) to calculate exchange rates movements to preserve PPP.
After Cassel’s works strong criticisms against the PPP doctrine emerged. For instance, Keynes (1923, pp. 88-91) draws attention to the importance of considering the so-called transaction costs2, given that transport charges, import and export taxes, and tariffs represent a serious difficulty for the PPP doctrine. Moreover, Keynes (1930, p. 302) asserted that the PPP doctrine is close to a truism3, strongly objecting that “the neglect to allow for the effect of changes in the terms of trade is, perhaps, the most unsatisfactory characteristic of Professor Cassel’s Purchasing Power Parity Theory of the Foreign Exchanges”.
Along these lines, modern criticism focuses on the implausibility of the LoP in the context of international trade. Dornbusch (1985) notes that if the commodities comprising the baskets among countries are not the same, it is not reasonable to suppose the validity of the LoP in order to support the PPP hypothesis. Similarly, Shaikh (2016) points out that the PPP theory relies on two assumptions, namely 1) the baskets of goods should be homogeneous among countries, and 2) the price ratio between non-tradable/tradable goods should be the same in those countries that are trading with one another.
At an empirical level, if both assumptions are not fulfilled in the actual world, the real exchange rates would not be stationary variables at all, thereby contravening the PPP doctrine. Inspired by this theoretical and empirical discussion, the present study is aimed at testing the PPP hypothesis for 28 Organization for Economic Cooperation and Development (OECD) countries over the period 1960Q1-2021Q1. To the best of our knowledge, the novelty of this research consists of being the first attempt to empirically evaluate whether the bilateral real exchange rates for the selected OECD countries are stationary variables applying unit-roots tests, both in time series and panel data.
The remainder of the paper is organized as follows. Section 2 briefly discusses the PPP theory in the modern literature. Section 3 presents the source of our data and the unit-roots tests to be utilized. Section 4 presents and critically evaluates the results obtained. Section 5 summarizes and makes some concluding remarks.
2. The PPP hypothesis in the modern literature
Since Cassel’s works appeared in the early twentieth century, the PPP hypothesis has been tested employing different statistical and econometrics methods (Bahmani-Oskooee, Chang, and Lee, 2016; Banerjee, Marcellino, and Osbat, 2005; Caner and Kilian, 2001; Doğanlar, Kızılkaya, and Mike, 2020; Kapetanios, Shin, and Snell, 2003; Kapetanios and Shin, 2008; Lothian and Taylor, 2008; Pedroni, 2001; Taylor, 2006; Taylor, Peel, and Sarno, 2001). However, in the modern literature, there is no consensus on its validity. As Taylor and Taylor (2004) remark, the debate is still ongoing and lively, insofar as some issues such as the existence of non-tradable commodities (the so-called Harrod-Balassa-Samuelson effect), transaction costs or heterogeneous compositions of goods bundles constitute crucial challenges both at the theoretical and empirical level.
According to those authors, the evidence in favor of the PPP hypothesis appears to be weak. For instance, in time series analysis the rejection of the null hypothesis that a unit root exists might not prove that the actual exchange rates tend to converge to PPP since “the long-span studies raise the issue of possible regime shifts and whether the recent evidence may be swamped by history” (Taylor and Taylor, 2004, p. 146). Furthermore, the rejection of the null hypothesis using panel unit root tests may derive from “a few mean-reverting real exchange rates within the panel” (Taylor and Taylor, 2004, p. 146).
Similarly, Banerjee, Marcellino, and Osbat (2005, p. 79) reveal that the panel data assessments tend to over reject the null hypothesis of non-stationarity because of the oversizing emerged from cointegrating relationships rather than the higher power of panel unit root tests. In addition, Taylor (2006) draws attention to shortcomings related to traditional econometric techniques based on ordinary least squares and instrumental variables estimation.
As noted by Taylor, these approaches tend to incur the so-called spurious regression problem. Even by first-differencing the series, these traditional techniques fail to obtain robust statistical results to support the PPP theory because the long-run relationship between variables is removed. Taylor (2006) also observed that the first generation of unit root tests provided mixed results. For instance, Taylor (1988) and Mark (1990) found that real exchange rates are non-stationary, while Huizinga (1987) and Chowdhury and Sdogati (1993) reject the null hypothesis of unit root. Thus, the first PPP puzzle consists in the absence of robust empirical evidence for the long run.
Rogoff (1996, p. 647) identifies the second PPP puzzle, namely, the inconsistency between the short run volatility of the real exchange rate and its slow adjustment to PPP in the long run. It is worth mentioning that most volatility in the short run may be attributable to financial factors (e.g., portfolio preferences, asset price bubbles, and monetary shocks) [Obstfeld and Rogoff, 1996]. Likewise, Rogoff (1996, p. 648) argues that most empirical studies propose a half-life of three or five years to measure real exchange rates’ adjustment to PPP, which is “far too long to be explained by normal rigidities”. Then, this very slow speed of adjustment to PPP is tough to reconcile with the short run volatility (Taylor, 2006).
On the other hand, the absolute version of the PPP hypothesis faces the colossal problem of gathering information to measure it. As Rogoff (1996, p. 650) discloses, governments do not build indices for an internationally standardized bundle of commodities, which means that the LoP should be refused, thereby affecting the validity of the absolute PPP. The second problem lies in the fact that indices cannot measure how large absolute PPP deviations were from the base year. Therefore, those tests based on aggregate price indexes overwhelmingly reject the absolute PPP as a short run relationship4 (Rogoff, 1996).
To solve this difficulty, in the empirical literature there is a preference for testing the relative PPP. This version only requires changes in relative price levels to be offset by changes in the exchange rate (Froot and Rogoff, 1995). Nevertheless, Shaikh (2016, p. 527) states that even this relative PPP cannot be a general empirical proposition because, graphically, the real exchange rates show deterministic time trends in the short and long run.
Conversely, several studies found strong empirical evidence supportive of the relative PPP in high inflation economies (Barro, 1997; Frenkel, 1978; Froot and Rogoff, 1995; Isard, 1995). According to Shaikh (2016, pp. 526-527), this result appears to be consistent with the classical political economy theory of trade. Given that the differences in real wages and labor productivities among countries are rigid, slight variations in prices suggest that the relative PPP will not hold. On the contrary, in a hyperinflationary scenario, the changes in nominal exchange rates will correspond to relative inflation. Shaikh (2016, p. 527), hence, objects to Barro’s (1997, p. 542) findings outlined in his Macroeconomics textbook since they cannot be generalized to low inflation countries.
Shaikh (2016, p. 528) discloses that actual exchange rates are nonstationary because they are governed by relative unit production costs in the long run, explaining the slow adjustment observed by modern literature on the PPP theory. It should be noted that there exists abundant empirical evidence to support Shaikh’s hypothesis, insofar as real exchange rates appear to be governed in the long run by the relative vertically integrated unit labor costs (Boundi-Chraki and Perrotini-Hernández, 2021; Boundi Chraki, 2021; Martínez-Hernández, 2017; Tsaliki, Paraskevopoulou, and Tsoulfidis, 2018; Tsoulfidis and Tsaliki, 2019). Thus, Shaikh’s theoretical explanation may respond satisfactorily to the inquiry of why the PPP hypothesis does not hold in the actual world.
Nonetheless, modern empirical literature retrieved Heckscher’s (1916) proposition that adjustment is likely nonlinear due to transaction costs in international arbitrage. Following Heckscher’s insight, Obstfeld and Taylor (1997), who analyze a set of consumer price subindices, discover that there exist statistically significant nonlinearities. Along these lines, Taylor, Peel, and Sarno (2001) use Granger and Teräsvirta’s (1993) logistic and exponential smooth transition autoregressive (LSTAR and ESTAR, respectively) models by to capture the nonlinear adjustment. According to their results, it is feasible to reject the hypothesis of a unit root in favor of the alternative hypothesis of nonlinearly mean reverting, solving prima facie the so-called PPP puzzle.
Similarly, Lothian and Taylor (2008), who apply the ESTAR model and long-span data starting in 1820 for the United States (US), the United Kingdom (UK) and France, conclude that there are significant nonlinearities in adjustment for real exchange rates. Lastly, Kapetanios, Shin, and Snell (2003) appraise the PPP doctrine for the 11 major OECD countries applying the nonlinear STAR tests and the linear Dickey-Fuller tests. Their findings suggest the existence of nonlinear mean-reversion, whereas those tests based on Dickey-Fuller fail to reject the null hypothesis of a unit root process.
3. Data and methods
All the information to assess the validity of the PPP hypothesis was gathered from the OECD statistics database. Through this data source, we obtained the consumer price indices (CPIs5) and the nominal exchange rates over the period 1960Q1-2021Q1 for 28 OECD countries6 (see Table 1). Note that the nominal exchange rates correspond to the relationship between the national currency of the countries summarized in Table 1 and the United States dollar7 (USD).
Table 1 Sample
| Austria | Denmark | Italy | Norway |
| Australia | Finland | Japan | Portugal |
| Belgium | France | Korea | Spain |
| Canada | Germany | Luxembourg | Sweden |
| Chile | Greece | Mexico | Switzerland |
| Colombia | Iceland | Netherlands | Turkey |
| Costa Rica | Ireland | New Zealand | United Kingdom |
Source: Authors’ elaboration.
To test the PPP hypothesis, the real exchange rates are computed as:
Where ɛ t stands for the nominal real exchange (national currency/USD), P t * represents the CPI of the US, P t is the CPI of each OECD country included in the analysis, while t refers to the period (t = 1960Q1, 1961Q2, …, 2021Q4). Taking logarithms, obtains:
According to the PPP hypothesis, Log(RER t ) should be zero because the movements of the actual exchange rates are equivalent to deviations from PPP (Taylor, 2006, p. 4). That is, Log(RER t ) should be stationary -at level- for the PPP hypothesis to hold. To examine whether the real exchange rates are stationary, three types of unit root tests are used.
First, the empirical assessment starts by implementing the classical unit root tests for time series data, namely, the Augmented Dickey-Fuller (ADF, 1981), the Phillip-Perron (PP, 1988), and the Kwiatkowski-Phillips-Schmidt-Shin (KPSS, 1992). Both the ADF and PP check the null hypothesis that the variable contains a unit root against the alternative hypothesis that the variable follows a stationary process.
Nonetheless, the PP is more robust than the ADF, insofar as the former applies Newey-West (1987) standard errors to control for serial correlation, while the latter uses additional lags of the first-differenced variable. By contrast, The KPSS checks out the null hypothesis of stationarity, though it suffers from some disadvantages regarding ADF and PP (Shin and Schmidt, 1992). The literature points out that the major weakness of the KPSS consists of its tendency to over-reject the null hypothesis because it often incurs type I errors. Thus, the KPSS’s results should be considered complementary to those obtained from ADF and PP.
As a further step, we apply the panel unit root tests. As noted by Maddala and Wu (1999, p. 641), a panel unit root test may increase the power of those unit root tests based on time series. Panel unit root tests can be divided into two groups: The first generation and the second generation. The first generation of panel unit root tests is represented by Levin-Lin-Chu (LLC, 2002), Harris-Tsavalis (HT, 1999), Breitung (2000), Im-Pesaran-Shin (IPS, 2003), Choi (2001), Maddala-Wu (MW, 1999), and Hadri (2000).
It is interesting to note that while LLC, HT and Hadri require a balanced dataset, Breitung, IPS, Choi and mw fit in the face of an unbalanced dataset. Although these latter tests allow unbalanced panel data, those countries whose data do not cover the period 1960Q1-2021Q4 were discarded when we applied all the panel unit root tests to maintain consistency of the empirical assessment. On the other hand, given that Hadri is based on KPSS, tends to over-reject the null hypothesis of the individual series being stationarity. Therefore, Hadri’s outcomes will be regarded as complementary.
It should be emphasized that the first generation of panel unit roots neglects cross-sectional dependence, incurring in the so-called size distortion problem and leading to misleading results (Banerjee, Marcellino, and Osbat, 2005; Banerjee and Carrion-i-Silvestre, 2017; Pesaran, 2021). The conventional panel unit root tests, thus, overwhelmingly reject the null hypothesis of non-stationarity in the presence of cross-sectional dependence. To solve this limitation, Pesaran’s (2007) Cross-Sectional Augmented Im, Pesaran and Shin (CIPS) test is used.
Lastly, given that the nonlinear adjustment towards PPP may arise due to international frictions, we apply the detrending-based nonlinear unit root tests developed by Kapetanios, Shin, and Snell (KSS, 2003) and Kapetanios and Shin (KS, 2008). These tests check the null hypothesis of the unit root process against the alternative hypothesis of a nonlinear ESTAR process, though KSS uses the ordinary least square (OLS) detrending, whereas the KS applies the generalized least-squares (GLS) detrending (Otero and Smith, 2017).
4. Results
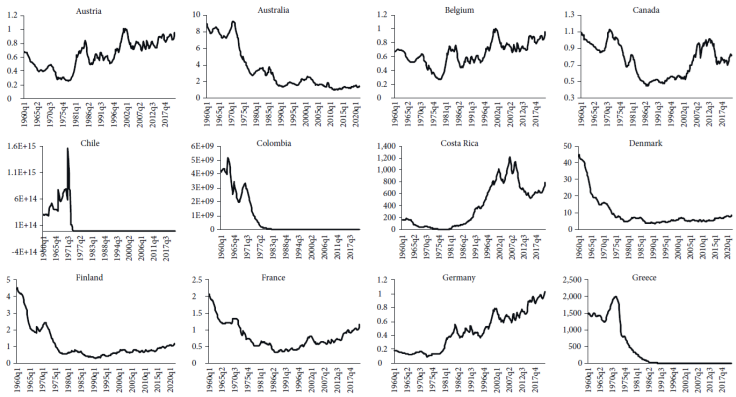
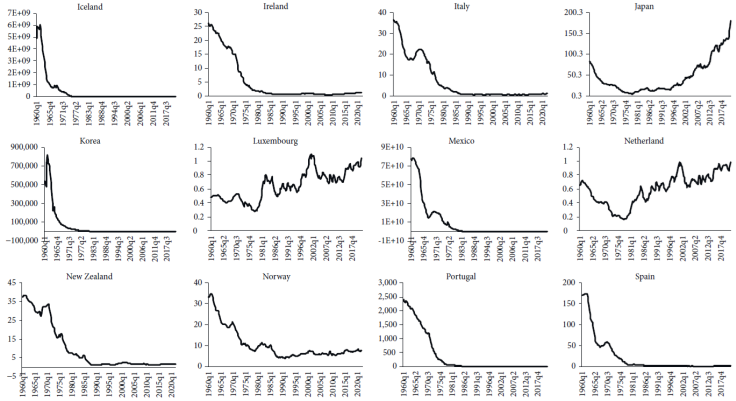
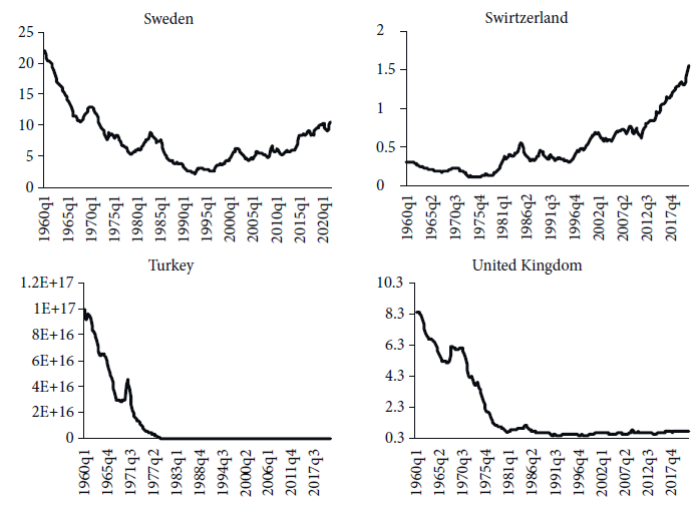
As noted in the econometrics literature, those variables exhibiting a tendency (both deterministic and stochastic) may contain a unit root. Graphs 1, 2, and 3 from the Appendix disclose that most of the real exchange rates vis-à-vis the USD exhibit a deterministic tendency, thereby suggesting that they might be non-stationary series. Since the graphical study does not suffice to conclude that real exchange rates are non-stationary, we examine whether there is a unit root using the ADF and PP tests.
Table 2 indicates that, absence a trend, the ADF can reject the null hypothesis for Denmark, Korea, Norway, and Spain when the trend is not included, whereas the PP rejects the null hypothesis for Denmark, Finland, Iceland, Ireland, Korea, Norway, and Spain. Conversely, if a trend is included to compute both ADF and PP, the null hypothesis cannot be rejected. It should be stressed that the real exchange rates appear to have a tendency, which means that the results with a trend may be considered more robust. Moreover, Table 3 shows that the KPSS test rejects the null hypothesis of stationarity, supporting that the real exchange rates contain a unit root. It is interesting to compare these findings with the results of prior investigations.
Table 2 ADF and PP panel unit root tests results
| ADF | pp | |||||||
|---|---|---|---|---|---|---|---|---|
| Country | Without trend | With trend | Without trend | With trend | ||||
| Statistic (z(t)) | p-value | Statistic | p-value | Statistic (Z (rho)) | p-value | Statistic (Z (rho)) | p-value | |
| Austria | -1.210 | 0.669 | -2.934 | 0.151 | -2.578 | 0.758 | -9.944 | 0.259 |
| Australia | -1.533 | 0.517 | -1.660 | 0.768 | -2.016 | 0.499 | -4.462 | 0.894 |
| Belgium | -1.652 | 0.456 | -2.617 | 0.272 | -4.052 | 0.646 | -8.415 | 0.501 |
| Canada | -1.527 | 0.520 | -1.231 | 0.904 | -3.361 | 0.511 | -2.656 | 0.912 |
| Chile | -1.664 | 0.450 | -0.880 | 0.958 | -1.425 | 0.271 | 0.045 | 0.995 |
| Colombia | -1.106 | 0.713 | 0.054 | 0.995 | -0.373 | 0.683 | 1.079 | 1.000 |
| Costa Rica | -0.483 | 0.895 | -1.823 | 0.694 | -0.277 | 0.935 | -3.067 | 0.732 |
| Denmark | -3.178 | 0.021** | -1.615 | 0.787 | -5.263 | 0.007*** | -2.900 | 0.820 |
| Finland | -2.528 | 0.109 | -1.255 | 0.898 | -4.287 | 0.053* | -2.020 | 0.915 |
| France | -2.010 | 0.282 | -1.153 | 0.920 | -4.330 | 0.212 | -2.343 | 0.920 |
| Germany | -0.379 | 0.913 | -2.465 | 0.346 | -0.287 | 0.936 | -7.841 | 0.497 |
| Greece | -1.277 | 0.640 | 0.239 | 0.996 | -0.664 | 0.549 | 1.557 | 1.000 |
| Iceland | -2.304 | 0.171 | -0.140 | 0.993 | -1.238 | 0.020** | 0.899 | 1.000 |
| Ireland | -2.541 | 0.106 | 0.095 | 0.995 | -2.366 | 0.033** | 0.548 | 0.997 |
| Italy | -2.420 | 0.136 | 0.370 | 0.997 | -2.043 | 0.108 | 0.791 | 0.997 |
| Japan | 0.169 | 0.970 | -2.490 | 0.333 | 0.559 | 0.982 | -3.747 | 0.284 |
| Korea | -3.989 | 0.002*** | -1.002 | 0.944 | -2.902 | 0.000*** | -1.223 | 0.959 |
| Luxembourg | -1.228 | 0.662 | -2.782 | 0.204 | -2.865 | 0.742 | -10.738 | 0.396 |
| Mexico | -1.085 | 0.721 | -0.846 | 0.962 | -0.494 | 0.705 | 0.376 | 0.996 |
| Netherlands | -0.973 | 0.793 | -2.439 | 0.359 | -1.497 | 0.846 | -5.707 | 0.552 |
| New Zealand | -1.668 | 0.448 | -0.964 | 0.949 | -1.656 | 0.425 | -0.889 | 0.986 |
| Norway | -2.701 | 0.074* | -1.548 | 0.812 | -4.202 | 0.080* | -2.949 | 0.897 |
| Portugal | -2.230 | 0.195 | 0.912 | 1.000 | -1.361 | 0.110 | 1.590 | 1.000 |
| Spain | -2.825 | 0.055* | -0.338 | 0.989 | -2.208 | 0.006*** | 0.476 | 0.997 |
| Sweden | -2.012 | 0.281 | -1.037 | 0.939 | -4.094 | 0.220 | -1.876 | 0.954 |
| Switzerland | 0.228 | 0.974 | -2.589 | 0.285 | 0.913 | 0.987 | -7.564 | 0.410 |
| Turkey | -0.578 | 0.876 | -1.098 | 0.929 | 0.043 | 0.970 | -1.146 | 0.948 |
| United Kingdom | -2.500 | 0.116 | -0.598 | 0.979 | -2.639 | 0.106 | -0.711 | 0.986 |
Note: *** Denotes rejection at 1%.
** Denotes rejection at 5%.
* Denotes rejection at 10%.
The ADF’s null hypothesis is a unit root is present in a time series sample. The pp’s null hypothesis is a unit root is present in a time series sample. Optimal lags were computed using the Akaike criteria. We applied the command dfuller and pperron implemented in Stata 17.
Table 3 KPSS unit root test results
| Country | Critical values | ||||
|---|---|---|---|---|---|
| Statistic | 10% | 5% | 1% | Decision | |
| Austria | 0.268 | 0.119 | 0.146 | 0.216 | Reject H0 |
| Australia | 0.618 | 0.119 | 0.146 | 0.216 | Reject H0 |
| Belgium | 0.366 | 0.119 | 0.146 | 0.216 | Reject H0 |
| Canada | 0.967 | 0.119 | 0.146 | 0.216 | Reject H0 |
| Chile | 1.02 | 0.119 | 0.146 | 0.216 | Reject H0 |
| Colombia | 0.595 | 0.119 | 0.146 | 0.216 | Reject H0 |
| Costa Rica | 0.535 | 0.119 | 0.146 | 0.216 | Reject H0 |
| Denmark | 1.06 | 0.119 | 0.146 | 0.216 | Reject H0 |
| Finland | 1.11 | 0.119 | 0.146 | 0.216 | Reject H0 |
| France | 1.13 | 0.119 | 0.146 | 0.216 | Reject H0 |
| Germany | 0.345 | 0.119 | 0.146 | 0.216 | Reject H0 |
| Greece | 0.789 | 0.119 | 0.146 | 0.216 | Reject H0 |
| Iceland | 1.13 | 0.119 | 0.146 | 0.216 | Reject H0 |
| Ireland | 1.15 | 0.119 | 0.146 | 0.216 | Reject H0 |
| Italy | 1.11 | 0.119 | 0.146 | 0.216 | Reject H0 |
| Japan | 1.04 | 0.119 | 0.146 | 0.216 | Reject H0 |
| Korea | 1.12 | 0.119 | 0.146 | 0.216 | Reject H0 |
| Luxembourg | 0.245 | 0.119 | 0.146 | 0.216 | Reject H0 |
| Mexico | 0.716 | 0.119 | 0.146 | 0.216 | Reject H0 |
| Netherlands | 0.448 | 0.119 | 0.146 | 0.216 | Reject H0 |
| New Zealand | 0.997 | 0.119 | 0.146 | 0.216 | Reject H0 |
| Norway | 1.04 | 0.119 | 0.146 | 0.216 | Reject H0 |
| Portugal | 1.14 | 0.119 | 0.146 | 0.216 | Reject H0 |
| Spain | 1.17 | 0.119 | 0.146 | 0.216 | Reject H0 |
| Sweden | 1.07 | 0.119 | 0.146 | 0.216 | Reject H0 |
| Switzerland | 0.352 | 0.119 | 0.146 | 0.216 | Reject H0 |
| Turkey | 0.617 | 0.119 | 0.146 | 0.216 | Reject H0 |
| United Kingdom | 1.15 | 0.119 | 0.146 | 0.216 | Reject H0 |
Note: The KPSS’s null hypothesis is RER is trend stationary. The maximum number of lags was chosen by Schwert criterion. We used the KPSS command by Baum (2000).
For instance, Banerjee, Marcellino, and Osbat (2005) find that the ADF fails to reject the null hypothesis in real exchange rates for 18 OECD countries. Similarly, Kapetanios, Shin, and Snell (2003) also disclose that the linear ADF test is not capable of rejecting the null hypothesis of a unit root in real exchange rates for the 11 major OECD countries. Caner and Kilian (2001) reveal that the KPSS test rejects the null hypothesis for 17 OECD countries when the sample is organized with quarterly data.
Nevertheless, our results should be treated cautiously, since we face some limitations derived from the application of conventional unit root tests in time series. More precisely, ADF, PP and KPSS lack power in the presence of structural breaks and potential nonlinear adjustments, and they are size distorted (Caner and Kilian, 2001; Froot and Rogoff, 1995).
To increase the confidence of our results, we grouped individual real exchange rates as a panel data. As can be seen in Table 4, when we do not include a trend, only LLC and Choi suggest the rejection of the null hypothesis of a unit root. On the contrary, the null hypothesis cannot be rejected by none of first-generation panel unit root tests when a trend is included. Note also that the Hadri test rejects the null hypothesis of stationarity both without and with a trend. However, it should be underlined that the first generation of panel unit root lacks power in presence of cross-sectional dependence.
Table 4 Panel unit root tests results
| Test | Without trend | With trend | ||||
|---|---|---|---|---|---|---|
| Statistics | p-value | Statistics | p-value | |||
| Unadjusted t | -5.543 | Unadjusted t | -2.285 | |||
| LLC | Adjusted t* | -4.619 | 0.000*** | Adjusted t* | 7.596 | 1.000 |
| HT | Rho | 0.999 | 1.000 | rho | 0.999 | 1.000 |
| Breitung | lambda* | 8.573 | 1.000 | lambda* | 7.158 | 1.000 |
| IPS | W-t-bar | 2.462 | 0.993 | W-t-bar | 10.301 | 1.000 |
| Inverse chi-squared(56) P | 124.026 | 0.000*** | Inverse chi-squared(56) P | 115.602 | 1.000 | |
| Choi | Inverse normal Z | -5.940 | 0.000*** | Inverse normal Z | 7.842 | 1.000 |
| Inverse logit t(144) L* | -5.850 | 0.000*** | Inverse logit t(144) L* | 8.439 | 1.000 | |
| Modified inverse chi-squared Pm | 6.428 | 0.000*** | Modified inverse chi-squared Pm | -4.199 | 1.000 | |
| Inverse chi-squared(56) P | 47.446 | 0.785 | Inverse chi-squared(56) P | 8.129 | 1.000 | |
| MW | Inverse normal Z | 2.185 | 0.985 | Inverse normal Z | 7.121 | 1.000 |
| Inverse logit t(144) L* | 2.247 | 0.987 | Inverse logit t(144) L* | 7.719 | 1.000 | |
| Modified inverse chi-squared Pm | -0.808 | 0.790 | Modified inverse chi-squared Pm | -4.523 | 1.000 | |
| Hadri | Z | 131,898 | 0.000*** | Z | 81.288 | 0.000*** |
| t-bar | -3.153 | t-bar | -1.973 | |||
| Pesaran CIPS | Z[t-bar] | -7.927 | 0.000*** | Z[t-bar] | -1.066 | 0.143 |
Note: *** Denotes rejection at 1%. ** Denotes rejection at 5%. * Denotes rejection at 10%. Optimal lags were computed using the Akaike criteria. The null hypothesis for LLC, HT, and Breitung tests is panels contain unit roots. The null hypothesis for Choi and mw tests is all panels contain unit roots. MW’s null hypothesis is all panels contain unit roots. Hadri’s null hypothesis is all panels are stationaries. Pesaran CIPS’ null hypothesis is all panels contain unit roots. For the first generation of panel unit root tests, we used the command xtunitroot included in Stata 17. To compute the Pesaran CIPS test, the multipurt routine by Eberhardt (2011) based on Lewandowski’s (2007)pescadf was applied.
To solve this limitation, the Pesaran CADF test is applied. According to Table 4, if a trend is excluded from the analysis, the Pesaran CIPS test rejects the null hypothesis. By contrast, this test fails to reject the null hypothesis when a trend is included. Given that graphs from the Appendix suggest that the real exchange rates may follow a deterministic tendency, the results obtained with a trend should be considered more robust. Like ADF, PP, and KPSS, panel unit root tests do not consider the potential nonlinear adjustments toward PPP. Thus, the next step of our assessment involves interpreting the results obtained from the KSS and ks nonlinear unit root tests.
Table 5 outlines the outcomes of employing the KSS and KS, indicating that in most cases we cannot reject the null hypothesis of a unit root. More precisely, the KSS test suggests that we can reject the null hypothesis only for 6 OECD countries (i.e., Denmark, Finland, Ireland, Korea, Norway, and Spain), while the ks test indicates the null hypothesis could be rejected for 8 OECD countries (i.e., Denmark, Finland, Ireland, Iceland, Korea, Norway, Spain, and Sweden). Hence, even if the potential nonlinear adjustment is considered, the empirical evidence appears to refuse the PPP doctrine. Interestingly, our findings differ from those obtained by Kapetanios, Shin, and Snell (2003) and Kapetanios and Shin (2008), because they could reject de null hypothesis for 11 and 27 OECD countries, respectively.
Table 5 Nonlinear unit root tests results
| KSS | KS | |||
|---|---|---|---|---|
| Country | KSS statistics | p-value | KS statistics | p-value |
| Austria | -1.247 | 0.973 | -1.543 | 0.922 |
| Australia | -1.993 | 0.466 | -2.447 | 0.104 |
| Belgium | -0.643 | 0.666 | -0.135 | 0.672 |
| Canada | -1.035 | 0.033 | -2.462 | 0.820 |
| Chile | -1.158 | 0.415 | -2.364 | 0.357 |
| Colombia | -0.504 | 0.933 | -0.392 | 0.840 |
| Costa Rica | -1.044 | 0.752 | -0.686 | 0.613 |
| Denmark | -1.388 | 0.027** | -0.284 | 0.070* |
| Finland | -2.285 | 0.086* | -0.393 | 0.084* |
| France | -1.014 | 0.447 | -0.945 | 0.263 |
| Germany | -0.348 | 0.492 | -1.451 | 0.064 |
| Greece | -1.058 | 0.704 | -0.750 | 0.691 |
| Iceland | -1.032 | 0.054 | -0.802 | 0.028** |
| Ireland | -0.597 | 0.033** | -0.515 | 0.029** |
| Italy | -1.911 | 0.898 | -2.027 | 0.355 |
| Japan | -2.280 | 0.316 | -1.417 | 0.652 |
| Korea | -0.944 | 0.005*** | -0.278 | 0.096* |
| Luxembourg | -1.233 | 0.709 | -0.234 | 0.532 |
| Mexico | -0.301 | 0.225 | -1.124 | 0.302 |
| Netherlands | -0.450 | 0.091 | -2.453 | 0.817 |
| New Zealand | -1.264 | 0.551 | -2.270 | 0.272 |
| Norway | -0.227 | 0.048** | -0.057 | 0.047** |
| Portugal | -0.624 | 0.601 | -1.938 | 0.746 |
| Spain | -0.171 | 0.022** | -0.375 | 0.048** |
| Sweden | -1.739 | 0.615 | -1.132 | 0.089* |
| Switzerland | -1.773 | 0.677 | -2.418 | 0.973 |
| Turkey | -1.316 | 0.637 | -0.938 | 0.576 |
| United Kingdom | -1.293 | 0.368 | -1.796 | 0.864 |
Note: *** Denotes rejection at 1%. ** Denotes rejection at 5%. * Denotes rejection at 10%. Optimal lags were computed using the Akaike criteria. KSS and the KS tests were computed by using the commands kssur and ksur by Otero and Smith (2017).
These differences may arise due to two reasons. Our data incorporate more periods than Kapetanios, Shin, and Snell (2003) and Kapetanios and Shin (2008). While our research encompasses the period 1960Q1-2021Q4 (t = 244), Kapetanios, Shin, and Snell (2003) use data covering the period 1957Q1-1998Q4 (t = 164), and Kapetanios and Shin (2008) employ data spanning 1960Q1-2000Q4 (t = 160).
Another significant difference consists of the currency used to quote bilateral real exchange rates. Although Kapetanios, Shin, and Snell (2003, p. 369) analyze the bilateral real exchange rate with the USD, Kapetanios and Shin (2008, p. 379) examine the stationary properties of the yen and Deutsche mark real exchange rates. As Papell and Theodoridis (2001) and Banerjee, Marcellino, and Osbat (2005, p. 87) note, the currency chosen to conduct the analysis may change the results. On the basis of the above, it can be concluded that traditional unit root tests in time series, panel unit root tests, and nonlinear unit root tests seem to contravene the PPP hypothesis.
5. Concluding remarks
This research conducted an empirical assessment to test the validity of the PPP doctrine for 28 OECD countries and the world's largest economy, namely the United States. After a brief review of the theoretical foundations of the PPP hypothesis and the current-state-of-the-art literature, we disclosed that the debate between the proponents of the PPP theory and its detractors is still very lively, leading us to examine its fulfillment in the real world using those econometrics techniques applied in prior investigations.
Dividing the empirical analysis into three parts, the results obtained through the applications of conventional unit root tests and panel unit root tests were quite similar to those of other studies. The null hypothesis of a unit root could not be rejected for most cases, suggesting that the actual exchange rates may be non-stationary variables. Nonetheless, as noticed in the literature, international trade faces barriers such as tariffs, transport costs and taxes, which hinder the real exchange rates convergence toward PPP in the long run. Therefore, conventional unit root tests lack power if we assume that the adjustment toward PPP is nonlinear.
According to the literature, the so-called PPP puzzle could be resolved by including nonlinear techniques. However, both nonlinear KSS and ks tests disclosed that the actual exchange rates of several OECD countries with the USD are non-stationary, contravening previous studies. This apparent breach of the PPP hypothesis could have some policy implications insofar as conventional policies of exchange rates implemented by central banks maybe should be reformulated to avoid inaccurate previsions. Given that we must be cautious before reaching any conclusions about the validity of the PPP doctrine, further research should improve the power of the empirical assessment applying quantile unit root tests and nonlinear cointegration techniques.











 nueva página del texto (beta)
nueva página del texto (beta)