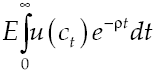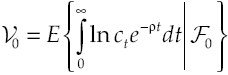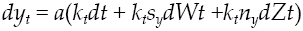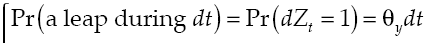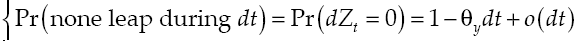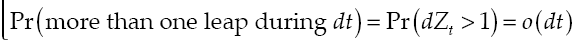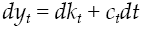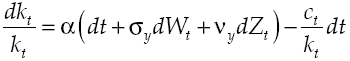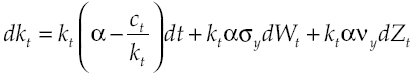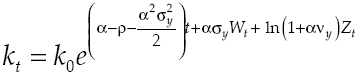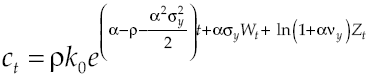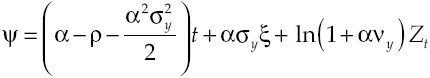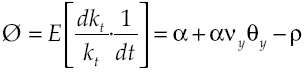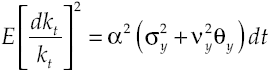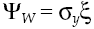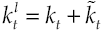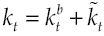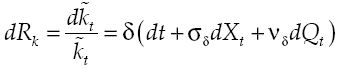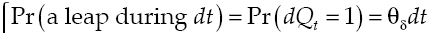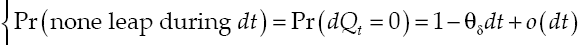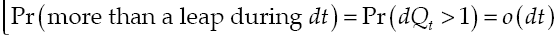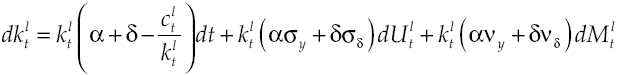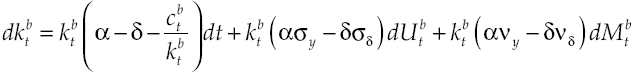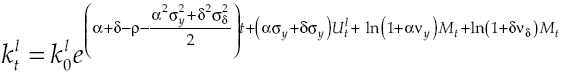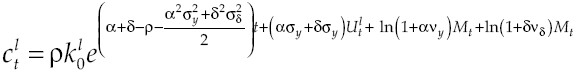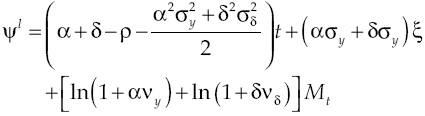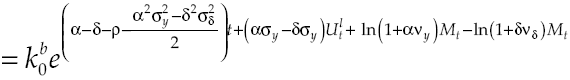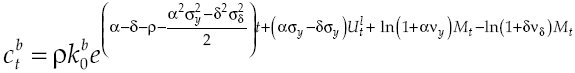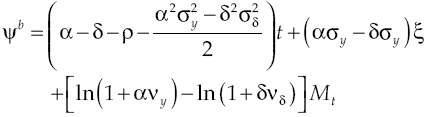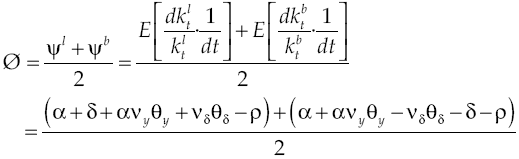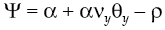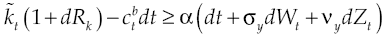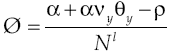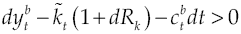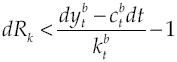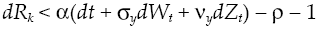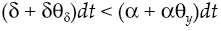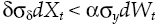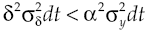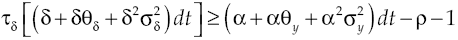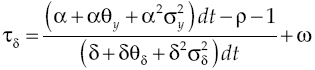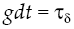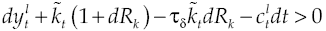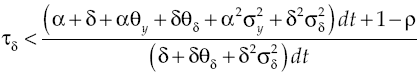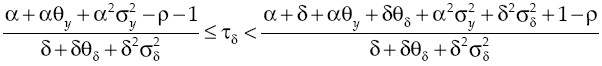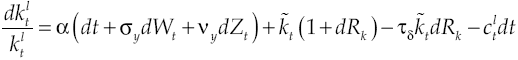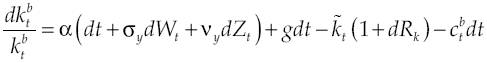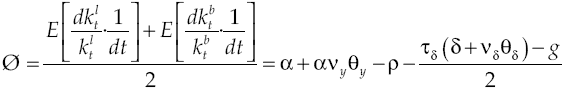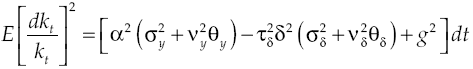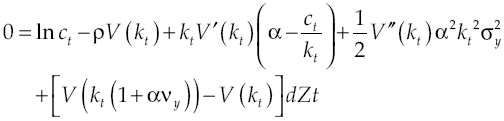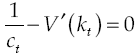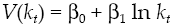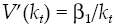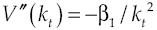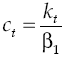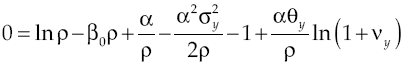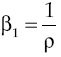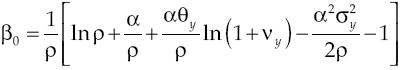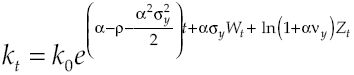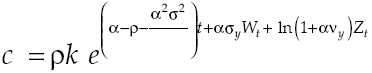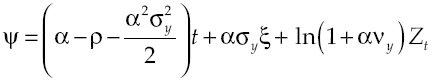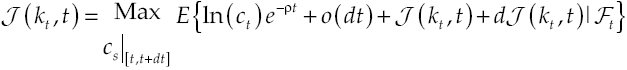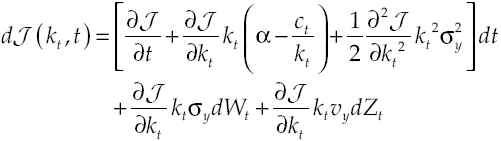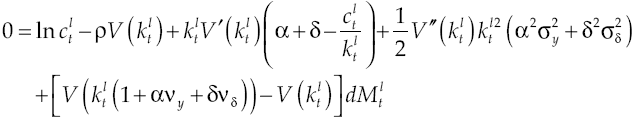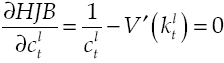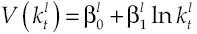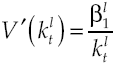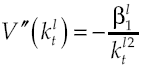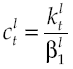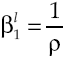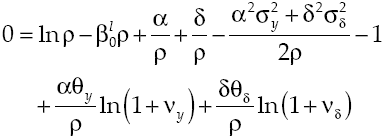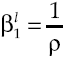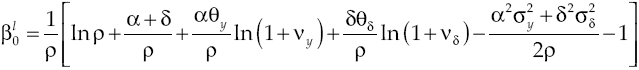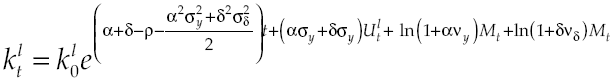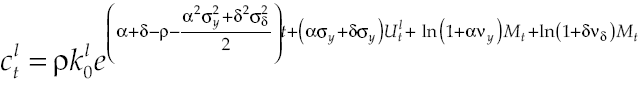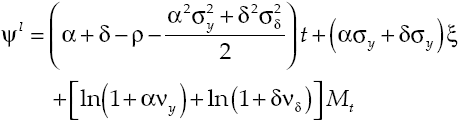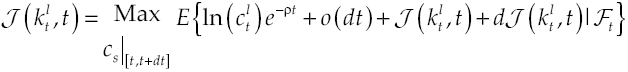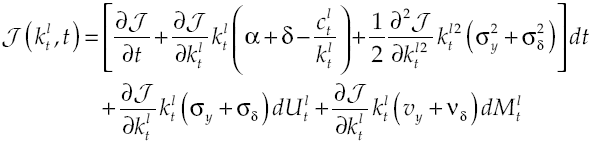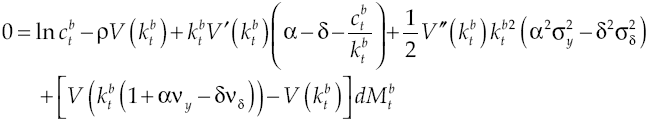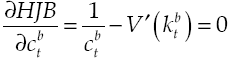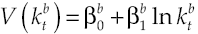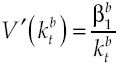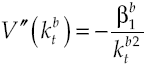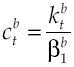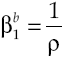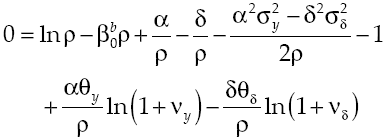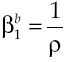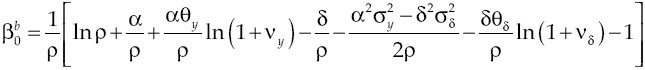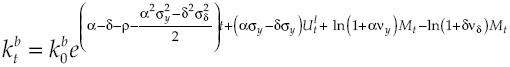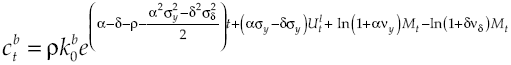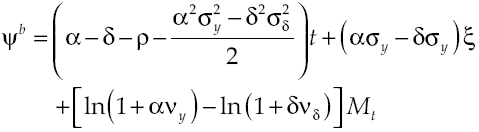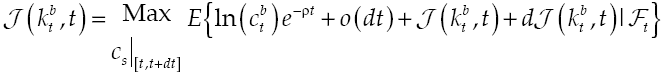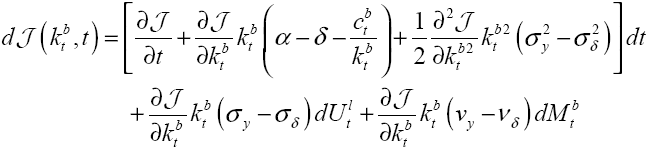JEL Classification: E44; G10; G14; G18; O40.
Clasificación JEL: E44; G10; G14; G18; O40.
Introduction
It is known that there is a link between financial system and real economy as Bagehot (1873), Gurley and Shaw (1955) and McKinnon (1973) showed. Furthermore, there are studies that revealed positive impacts on real economy due to a solid financial system, that is without inefficiencies such as credit constrains. Banerjee and Newman (1993), Galor and Zeira (1993), Aghion and Bolton (1997) and Piketty (1997) exposed that a financial sector can promote both physical and human capital accumulation under credit constraints conditions and nevertheless stimulates growth. On the other hand, Benabou (1993, 1996a, 1996b), Durlauf (1996a, 1996b), Fernández and Rogerson (1994, 1996), Kremer and Maskin (1994), Rivas-Aceves and Martínez Pérez (2011) and Rivas-Aceves (2012) uncovered that credit constraints and any other financial inefficiencies actually inhibits capital accumulation.
Herein it will be seen that relationship between financial system and real economy is favorable, positive or direct, if credit constraints and inefficiencies of financial sector are not present. This is consistent with the results found by the second approach described above. Consequently, the linkage is negative when financial system is not efficiently while reallocating resources in its possession, as a result a negative impact on economic growth takes place.
There have been several studies that show main conditions needed to minimize or even disappear negative impacts on real economy caused by an inefficient financial system. Some of them introduce government into economic system to regulate capital markets, see Barth, Caprio and Levine (2001a, 2001b, 2004, 2006), Levine (2011), La Porta, López-de-Silanes and Shleifer (2005), and Rivas-Aceves (2012).
The present analysis extends in two different ways the one carried out by Rivas-Aceves (2012) as follow: First, the theoretical model has been extended by using an stochastic growth model with a geometric Brownian motion plus Poisson jumps, this allows to analyze whether radical changes in marginal product of capital as well in capital yield affects macroeconomic equilibrium and therefore economic growth. Second, the research purports to further investigate the ultimate relationship between economic growth and financial systems regulations by a cross-section analysis based on data belonging to 40 developed and emerging countries and referring to the period ranging from 2000 to 2013. Regarding empirical evidence, De Serres et al. (2006) studied the effect of financial regulation on productivity growth and sectoral output. They used data at industry level of 25 Organisation for Economic Cooperation and Development (OECD) countries and tested whether the rate of growth of industries that largely rely on external financing is higher in countries that adopt competition-friendly policies in the financial systems and encourage the private sector to obtain credit from banks and financial institutions. They found a considerable variety of regulations depending on the country sampled but pointed to the significant role played by financial system regulation on growth both economically and statistically. A study made by Ulrich (2004) focused instead on Russian economy in the aftermath of the 1998 banking crisis and analyzed the spectacularly high growth rate following the financial crisis. It proved that real costs of crisis were indeed larger than reported but were offset by the recovery process and other expansionary factors. Furthermore, it verified the importance of financial system development in emerging and transition economies to stimulate growth.
However, previous empirical studies over the last decade have evolved in line with the prevailing theoretical models but concentrated on a period of favorable economic conditions, failing to verify whether major external shock or financial crises can potentially disrupt or significantly change the relation-ship found. Sinha (2012) concentrated on the link between macroeconomic policies and financial sector in monitoring and regulating financial markets before, during and after a crisis. The study supports that regulations on capital in Basel II and III will eventually boost banking systems without abandoning prudent and rigorous regulation and will contain risk exposure favoring at the same time macroeconomic stability.
The research is organized as follows: in Section 2 the basic economic system is described. Section 3 shows possible impacts on growth of an inefficient financial market. With an inefficient financial system, negative effects can be corrected by government intervention through financial regulation. To model regulation a tax on excessive cost of capital is introduced in Section 4. At this point the results show that: a) there is a linkage between financial sector and real sector, b) the direction and magnitude of that relationship depends on financial system characteristics, c) if the financial system has a negative impact on growth, financial regulation reverses this phenomenon, and d) there is an optimal behavior of the tax on capital cost that allows to return to a sustained and balanced growth path with full employment. Then an empirical analysis is carried out in Section 5 in order to verify the relationship between economic growth and financial regulations, so that: e) there is a negative impact on growth due to a shocks from financial systems, f) highly returns from stock markets decreases economic growth rate, g) government regulations on financial system can inhibit negative impacts on growth. Finally, a mathematical Appendix is shown in Section 7 and the references in Section 8.
Basic economy
Based on Rivas-Aceves (2012) growth model, this section develops an extended model by using a geometric Brownian motion with Poisson jumps set on the two fundamental economy sectors: real and financial ones, so production conditions and capital yield perform under uncertainty environments.
Homes
As in a canonical model, households are made up of consumers seeking to maximize the expected value of their utility due to consumption of a perishable commodity, which is measured by:
where utility function u(c t ) met with u’(c t ) > 0 and u’’(c t ) < 0, in other words, has decreasing marginal yields. According to this definition, per capita consumption is represented by c t and ρ is the subjective discount rate that measures preferences on present consumption of a representative individual. Suppose a logarithmic utility function type u(c t ) = ln c t and in addition assume consumers have access to information for decision-making, which is available at all time t. Consequently, von Neumann-Morgenstern utility function separable at t = 0 which measures this behavior is:
with F 0 as the set of initial information and initial conditions of economic variables, that will be defined later.
Productive sector
Producers use all capital available k t , to produce the commodity, and is considered available in the sense that it has not been consumed, implying that the commodity can be used as a capital asset as well. Likewise, per capita production, which is quantified by y t , is conducted through a given technology by all producers, so production conditions are:
where α measures the expected average on marginal product of capital, σ y the expected productivity dispersion and v y a leap in productivity. Meanwhile, dW t is a Wiener process defined on a fixed space of probability which an increased filtration that met (Ω, F, (F t ) t≥0 , ℙ), with independent temporary increments, zero average and variance equal to the temporary increase, last dZ t is a Poisson process that characterizes the dynamics of a leap in productivity with θ y intensity so that:
Additionally is supposed dW t and dZ t are uncorrelated, and that initial number of leaps in productivity is Z 0 = 0, also there is a positive level of initial capital, k0, and besides consider that o(dt) measures the effects of variables that persist beyond t + dt, which are insignificant, so o(dt)/t→0 when t→0.
Aggregate behavior
Suppose that economic agents make decisions simultaneously regarding production and consumption, in other words, households are the owners of production means. Consequently, total production in the economy is intended to investment or consumption, i.e.:
Substituting equation [3] in [7] causes the accounting identity that determines capital accumulation dynamics for each economic agent, therefore:
Equivalently,
To make decisions agents simultaneously involved the knowledge of restriction [8’] and available information at t = 0 given by F0 = {k0,Z0}.
Macroeconomic equilibrium
Under the established conditions, representative agent makes decisions based on results obtained by the solution of the stochastic optimal control problem given by equations [2] and [8’], this solution (see Appendix) regards the following optimality trajectories:
Economic growth rate
Growth on this economy depends on how capital accumulation rises, condition determined by equilibrium route established in [9]. Moreover, equation [11] shows in detail the dynamic of growth, which has two components: deterministic and stochastic. By considering equation [8] and equation [11] the deterministic component can be measured:
For economy to grow is always needed that α + αvyθy > ρ, otherwise economic growth will decrease. More than that, an increase in the expected average of marginal product of capital or in intensity productivity leaps, increases economic growth rate. Meanwhile, the variability in the deterministic component of growth rate is:
This means that variability in growth rate depends on marginal product of capital variability and leap variance. On the other hand, stochastic component is:
The above equation shows that each temporary increase in the economy will directly affect the stochastic standard deviation of growth rate.
Financial system
Among the many objectives of a financial system in an economy, one of the most important is to guide funds from units or economic agents registering surpluses at the end of their economic activities in each period towards other units or economic agents that have registered deficits, thus to study financial system in its essential form money won’t be considered in this model since physical capital can behave also as money does. Based on this idea, the analysis in this section introduces financial system into economy.
Productive sector
In order to introduce the financial system, it is necessary to slightly modify the behavior of above already described economy, particularly in connection with initial endowments of economic agents, so assume that productive sector of the economy is now composed by two types of producers, namely: a producer who has the necessary capital amount to carry out his production activities, plus a remnant result of their surpluses registered in previous periods, and a second producer who does not possess the amount of capital needed to produce.
This implies that total population of the economy, N, which is assumed to
remain constant over time, is divided by two types of households that own
production means named lenders (l) and jointly make up total
capital stock of economy, in such a way that
where
Given that, is interesting to analyze the effect of financial system on growth, for simplicity in the analysis assume that financial system aims only in reallocate capital without obtaining a profit and does not perform any other activity. Because savings equals investment condition takes place up to now, and since agents live in a closed economy, borrower agent can go to apply for a loan regarding the capital needed to perform his production activities. It is supposed that the amount of capital that lender agent placed into financial system is exactly equal to the amount of capital required by borrower agent, so that there are not lazy resources in the economy. This means that in order to produce borrower agent needs:
It will be assumed that there is a cost for credit1, so now capital
where dRk measures capital yield available in financial system, δ is the average yield expected, σδ represents yield volatility, vδ is a leap in the average yield expected, dXt is another Wiener process defined in a fixed space of probability that complies with augmented filtration (Ω, F, (Ft)t≥0, ℙ), with an independent temporary increases, zero average and variance equal to the temporary increase, meanwhile dQt is a new Poisson process characterizing the dynamics leap into the capital yield, with an intensity θδ so that:
Process dXt and dQt are uncorrelated, initial number of leaps in capital
yield is Q0 = 0. Consequently, lender agent will get at the end of every period
where dUt and dMt are Poisson
diffusion processes that results from the modification of capital accumulation
equation, for lenders and borrowers respectively, and also all the processes
involved are not correlated each other. Now, making decisions by representative
agents consider restrictions [21] and [22] and information available at
t = 0 determined by
Macroeconomic equilibrium
To determine macroeconomic equilibrium, it is needed to establish the balance of the household sector, which under the established conditions is the same for borrowers and lenders, and is ruled by the same scheme that previous section provided. Macroeconomic equilibrium now relies on individual equilibrium of both types of producers.
Economic growth rate
The economic growth rate, when there is a capital market, relies on the average growth of both productive sectors lender and borrower, so that by considering equations [21], [22], [25] and [28] the deterministic component of growth is:
Equivalently,
The growth rate of an economy without financial system is exactly equal to that one with an efficient financial system; the preceding is verified because equations [12] and [30] are equal. This means that economy grows at the same rate when financial system allows the reallocation of capital so that all producers carry out their production processes. At first sight it may seem that the effect of the financial system on growth is zero, however this is not so because it depends on the level of capital cost at the financial system, a scenario that will be discussed in the next section. If deterministic component of growth is given by [30], then stochastic variability of growth rate is equal to conditions [13] and [14].
Credit constraints and inefficiency of financial system
In previous section it was shown that economic growth rate of an economy with an efficient financial system is equal to that of a non-financial system economy. This is true as long as reallocating unused capital in the economy be the only function of financial system, nevertheless, if financial system is expanding its scope and is looking for a variety of activities with the aim of obtaining a profit derivative from resources management deposited in it, then it can generate inefficiencies within that market, which would increase cost of capital. This same consequence resulting from credit constraints, i.e., limiting the use of capital or little capital available for productive credit generates high capital costs.
And it is precisely a high cost that generates negative impacts on growth. Consider budget constraints set to borrower agent [21] and assume that cost of capital, determined by equation [17], is so high that causes the constraint to be zero or negative. In other words, to achieve
if this is so, then there are two possible scenarios, namely: first one is when a producer wants to maintain a fixed level of consumption and thus a high cost in capital leads to sacrificing its debt, and the second one is to keep up debt payments by sacrificing consumption. Under any scenario, producers has an incentive to not carrying out his economic activities since would not be optimal to do it because they will not obtain the necessary gains to survive, which implies in a fall of economic growth rate being that because borrower sector will not produce. If so, economic growth rate would be:
Obviously, the economic growth rate established in [31] is less than that set out in [30], i.e.
Government regulation
Everyone knows that if borrower agent does not obtain the missing capital to carry out his economic activities, then economic growth rate will be negatively affected, and this can only happen if capital cost is so high that capital accumulation in borrower sector becomes zero or negative. To prevent such a fall in the growth rate, it must be met:
Clearing for the cost of capital it is obtained:
At equilibrium, along equations [3], [26] and [27], capita cost must always fulfill:
The above equation shows that if capital cost is lower than the expected average of marginal product of capital for the borrower producer, discounting the subjective discount rate, then this agent will decide to hire credit and thus carry out production process. Substituting equation [17] in [34], the deterministic and stochastic components of the processes involved must meet respectively:
Suppose now that government takes part in the economy through regulation of financial system, with the exclusive purpose of preventing borrower industry to come out from economic activities and thus decreasing growth rate. To achieve this government can impose, at any time t, a tax ιδ, which represents the way in whereby government regulates financial system, it is not a tax figure in order to obtain resources to finance spending. This tax represents a proportion of capital cost whenever [34] is not fulfill, so:
Furthermore, defining a lower limit ω it can be determined that the tax of cost of capital in an inefficient financial system, is:
In addition, it can be assumed that government does not carry out any other activity, so its budget constraint is given by:
where g measures the level of per capita expected average spending made by the government in the form of production subsidies exclusively for borrower sector. This, due to an excessive increase on capital cost, government avoids the fall of economic growth rate through production incentives for borrower sector by subsidies financed precisely by capital yield under inefficient environments of financial system, credit constraints, or any other scenario that raises capital cost higher than the desired.
Optimal behavior of the tax cost of capital
As already discussed, government intervention occurs by a tax on capital yield when capital cost is too high. However, taxation must be paid by someone and as only the financial system or lender agents are subject to such a phenomenon, two possible scenarios can come about. The first occurs when financial system seeks to obtain profits due to discretional allocations of capital in his possession, causing two types of capital yields: the one that financial system obtains and the one lender receives from financial system, obviously with an existing gap between both, being lower the yield that lender receives. If so, then the financial system must undertake the cost of tax.
The second scenario is precisely originated when lender agent asks for a high payment due to the loan of his remaining capital; under this scenario tax must be borne by him. Nonetheless, tax cannot reach such a high level which causes capital accumulation in lender sector to be zero or negative, as if so growth rate of that sector would be negatively affected. Consequently, it met that:
If you are replacing into above equation equilibrium conditions [3], [23], [24], and if is considered deterministic and stochastic components of processes that represent both capital yield and product, and then clears for capital yield tax, then it is obtained:
Given that in equation [38] the parameter ω is unknown, then the level of tax cannot be determined and the lower limit depends on capital yield. However, considering conditions [37] and [41] it can be characterized an optimum range, per unit of time, within tax on capital can be placed, namely:
When government intervention is necessary thru a financial system regulation, the tax on capital yield should follow the optimal behavior determined by the equation above; this way government ensures the participation of both lender and borrower sectors in economic activities and thus will avoid the fall of economic growth rate.
Growth rate with financial regulation
So far it has shown how government intervenes in the economy if financial system has inefficiencies. With such an intervention capital accumulation equations from lenders and borrowers producers are modified, so that now:
Thus, deterministic economic growth rate is:
where, according to restriction [39], public components of the average in government spending and capital yield tax will be canceled. This implies that government regulation only generates the economy to develop at the growth rate set out in section “Aggregate behavior”. Even more, it can be verified clearly that government intervention only corrects the distortions caused by inefficiencies of financial system on the economy. Finally, variability in economic growth rate would be:
Similarly, condition [39] reverses the effects of regulation.
Empirical evidence
Data and methodology
The dataset collected for the analysis includes information belonging to 40 developed and emerging countries and referring to the period ranging from 2000 Government financial regulation and to 2013. The choice of the countries sampled in the study answers the need of giving a faithful and unbiased representation of real economy and is carried out by building a balanced set of an equal number of developed and developing countries2.
Annual growth rate of each considered country in the analysis is estimated and regressed on a subset of variables in order to evaluate whether a relation-ship between financial sector and economic growth can be found and how such correlation is affected by government regulation and fiscal policy. The period considered for the analysis is rather emblematic in this sense, so that it studies the change in global economy in the aftermath of the financial crisis of 2008 and highlights the difference in magnitude and significancy of coefficients estimated with particular focus on the pre-crisis period, commonly assumed to be particularly importance for the level of wellbeing, development and innovation.
To assess the interaction between financial system, growth rate and government intervention (through policies and regulations), a set of initial regressions is run to first identify the relationship each variable singularly has with the growth rate. This technique enables to evaluate which variables can be relevant for the analysis and how their coefficient changes as we allow them to vary once additional variables are included. The ultimate goal is to demonstrate how the underlying relationship can be affected by potential inefficiencies in the financial sector (proxied by financial variables), the level of existing regulation and government intervention (proxied by the Measures of Economic Freedom) and the impact on real economy by highlighting the trade-off between investments in the productive sector or in financial markets.
The study will thus divide the data collected in two periods based on whether they belong to pre-crisis (2000-2007) or post-crisis (2007-2013) period and differentiate the countries sampled in developed and developing. Any change in the sign, magnitude and significancy of coefficients between the two periods suggests that the aforementioned relationship is in fact sensitive to economy-wide and cross-country factors. Following is the list of variables employed for the model and the theoretical underpinning to justify their inclusion in the analysis.
Variables description
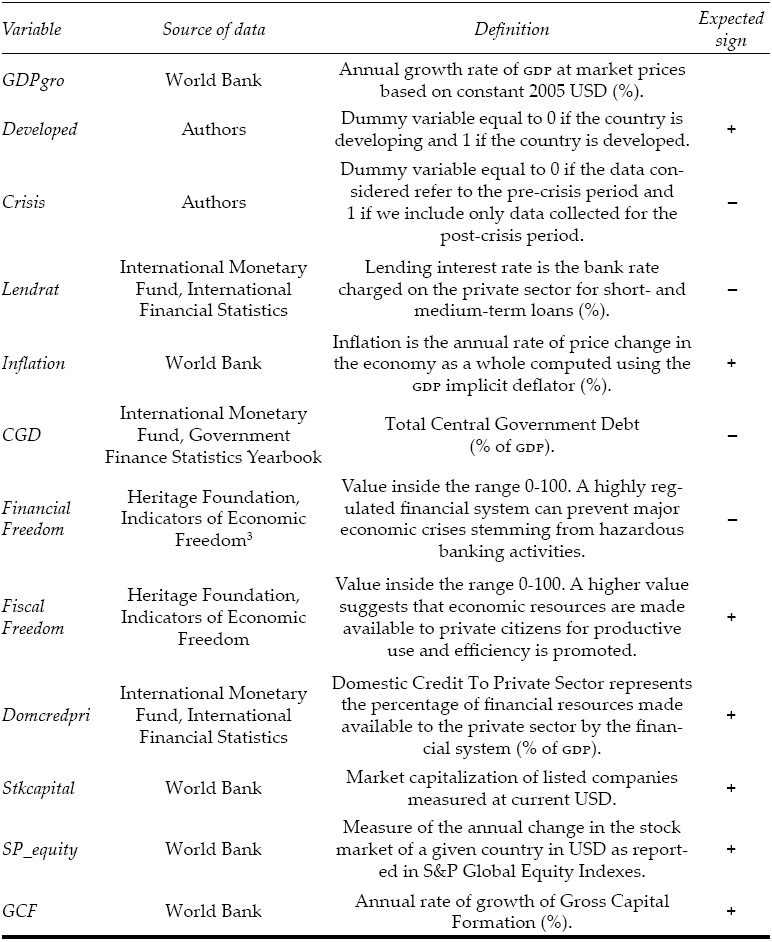
Gross Domestic Product growth (GDPGRO): The overall level of growth of each country can be reasonably proxied by the annual percentage change of nominal GDP as it is assumed to be a faithful representation of the resources and the uses of such resources of an economy.
Lending Rate: Lending Rate approximates the easiness of the private sector to meet their liabilities to the bank. A higher Lending Rate implies a lower demand, unfair terms of loans repayment and potential imperfections in the markets. It can either be directly set by administrative regulations or left to float on the market. Efficient and well-developed financial markets promote economic growth and constant flows of resources towards productive uses; information asymmetries and weaknesses in financial systems generate disruptions on the market, lower economic and financial activity (as demonstrated by trade volumes) and frictions in the creditor-debtor relationship, raising the lending interest rate to shield from unreliable borrowers.
Central Government Debt (CGD): This variable is measured as stock and not as flows and is negatively correlated with the level of growth. Lower debt fosters productivity, job creation and higher welfare at economy level. Moreover, a larger share of the budget is spent on basic service provision, funding, national private investments and initiatives targeting health, education, underserved communities and infrastructure.
Financial Freedom: The level of attractiveness of investments in financial markets rests on investors’ confidence, the existing regulation (entry and exit restrictions), institutional determinants, a potential securities and exchange commission, the law system protecting investors and ensuring liquidity of the stock traded. At the same time, reliable and easily accessible information and a competitive market promote transparency and smooth transfer of resources. However, when left unregulated, financial markets become subjects to speculations and hazardous operations, much as it happened during the 1929 Crisis. A prudent and rigorous regulatory system (reducing Financial Freedom) can ensure integrity of financial markets by requiring disclosure of assets, liabilities, overall level of risk-taking and critical operations, continuous monitoring and risk management. Were these regulations found to be excessive and unnecessary, they could hinder efficiency of financial markets and raise the cost of capital; however, they endeavor to prevent past financial shocks due mainly to deregulation from happening again in the future and this very reason justifies the chief critical importance of this variable in controlling growth rate.
Fiscal Freedom: In general, government control and monopoly constraints resources allocation and interferes with individual economic freedom, lowering their incentives to undertake business projects. Similarly, higher tax rates limit the ability of the private sector to engage in economic activity and can become burdensome for the nation as a whole.
Domestic Credit to Private Sector: Much as Domestic Credit provided by financial sector, it proxies the depth and extent to which financial markets are spread in the economy, promote investments and transfer of resources, and in particular money transmission, in the economy and indirectly boost the level of economic activity (consumption, production, capital formation). By providing credit to the private sector, resources are employed for socially useful purposes contribute to eradicate poverty in the least developed regions.
Stock Price: Market capitalization proxies the return on investments in financial markets and, more in general, stock market size and the development of an economy’s financial markets. A widespread and frictionless market can mobilize capital and investors’ funds based on their attitude to risk and their need for diversification. Moreover, by reducing information and transportation costs.
S&P Global Equity Indexes: Similarly, to Stock Price, this variable hints at the consequences that sound legal systems, exportled economies, macroeconomic stability have at attracting investments and cross-country capital flows, lowering cost of capital and enhancing liquidity in trade exchanges. Unlike the Stock Price measure, using a global indicator allows obtaining an approximate value of the overall financial performance of an economy and predicts fairly accurately the trend in emerging markets, proxying their market size. Temporary deviations, fads and imperfections can, however, produce a different ranking and result in a biased and distorted image of the existing financial markets.
Gross Capital Formation (GCF): Unlike investments in the financial markets through stocks, derivatives and other financial instruments, resources employed for the productive sector are earmarked for fixed-assets (equipment purchases, machinery and plant) and contribute to the overall level of capital acquisition. Physical capital is thus the backbone of agricultural and industrial economies alike, constituting a significant share of the economic activity and striving to achieve technological advance and innovation in these sectors. Finally, this paper assumes constant returns to scale, implying that the annual rate of growth of capital translates into an equal increase in production, income and, hence, GDP.
A list of the variables employed, their definition, the unit of measure, the source from which data were collected and the expected sign of their relation with the dependent variable is reported in Table 1.
Methodology
The research computes the estimates by using Ordinary Least Squares (OLS) up-to-date techniques. Notwithstanding the frequent substitution for proxy variables, the choice of regressors does not completely remove any bias caused by endogeneity problems and the small time period and sample size coupled with large fluctuations and external shocks generate dispersed values inside the range, increasing the overall variability, due also to the high heterogeneity of the countries analyzed, and reducing the predictability of the estimates.
The omitted variables bias, instead, is not found to be of main concern. Moreover, proxy variables can only be at most an approximation of the underlying relationship and arbitrary variables such as Fiscal Freedom, Gross Capital Formation, Financial Freedom can only to a certain extent represent the economic fundamentals they are underpinning. Several variables have not been included in the empirical analysis due to the unavailability or reliability of data and, when available, usually present particularly low t-statistics.
However, the results obtained prove the theoretical model and show a reasonably high level of significancy and consistency in the estimates. It would, then, be recommendable to extend the analysis to a larger set of countries, reduce the dispersion in the errors and contain the missing data problem. The estimated equation for the analysis is [45] described in section 4, while the empirical part related to government regulation refers to equation [60].
Results in the pre-crisis model
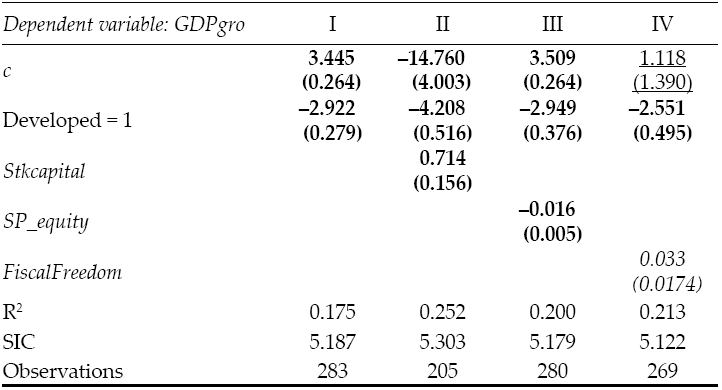
Table 2 refers to the analysis carried out for developed and developing countries focusing on the period ranging from 2000 to 2007. Column I shows separately the rate of growth for developed and developing countries and highlights the higher rate of growth for the latter (5.3%), suggesting that the first category has already reached its steady state equilibrium growth rate, while emerging economies are still catching up with rich countries due to their recent development. A regression using a constant instead of the dummy Developed = 0 was run but was not included here for sake of brevity and displays the same results found before.
Table 2: Pre-crisis model estimations
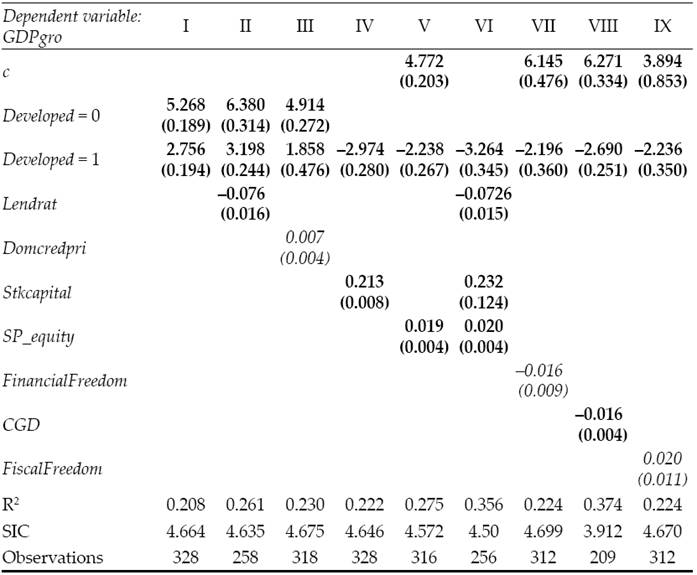
Note: bold: significancy < 0.01; underline: significancy < 0.05; cursive: significancy < 0.10.
Source: Own elaboration.
In Column II, it is directly tested the effect of Lending Rate (or equivalently for the cost of capital) and the coefficient estimated proves the negative relationship with growth rate at all levels of significancy, as demonstrated previously in the theory. Alternatively, the extent and depth of financial system (Domestic Credit to Private Sector) are found to be positively correlated with the dependent variable, even though only mildly (Column III). In order to assess the relationship between the stock market size and growth, Column IV and V compare the results found using respectively S&P Global Equity Indexes and the logarithm of market capitalization (Stkcapital). An initial regression was run using the level values instead of the logarithm of Stkcapital, resulting in an extremely low coefficient and low significancy and t-statistics due to the magnitude and broad dispersion of the values considered. Using log-values, instead, we obtain significant estimates at all levels, much as in Column V. Column VI summarizes the main results obtained related to evidence of the importance of the financial markets in determining growth and in particular the impact of potential imperfections and inefficiencies on the economy. Moreover, it highlights how the previous relationships hold once we include more variables, as shown by the high significancy of the estimates and the value of the goodness-of-fit (36%).
The second part of Table 2 analyzes the role of government in boosting growth. In particular, there is compelling evidence that lower Central Government Debt (Column VIII), higher Fiscal Freedom (Column IX) and a highly but not excessive regulatory system (Column VII) are beneficial to the economy, as shown in the theoretical part. It goes without saying that coercion and full control on economic freedom, property ownership, the rights to freely move labor, capital and goods beyond necessary are harmful for the economy and do not grant respect and protection on individual liberty and constraints resources allocation, undermining growth paths.
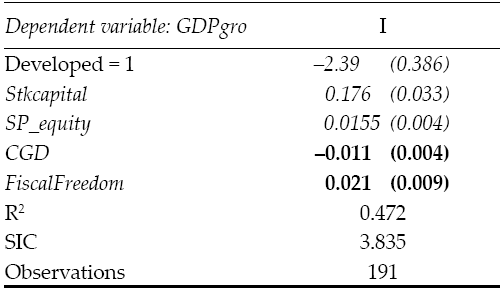
The full model in Table 3 indicates interactions between financial and public sector and the ultimate link with GDP growth. Some of the relationship found earlier do not hold once we account for a wider array of variables; however, the predictive power of the test is enhanced (R2 equal to 48%) and GDPgro is indeed determined by the market capitalization of shares, the extent and depth of financial markets, the size of Central Government Debt and the overall level of Fiscal Freedom in the economy.
Results in the post-crisis model
Most of the relationships found earlier in the paper do not hold in the post-crisis period. Single regressions were run to test for the significancy of Lending Rate, Financial Freedom and Domestic Credit to Private Sector; however, they were not found to be relevant and for sake of brevity were not reported here. The lower values of the goodness-of-fit is mainly due to the high variability characterizing the period, in particular the recession due to the financial crisis of 2007-8 and followed by a recovery of the worldwide economy in the second half of the period. Negative values found for the first part of the interval were offset by the positive amount of the last years, eliminating any possible results that could have been achieved. Moreover, high dispersion of the values assumed and the greater variance in the errors contributed to the poor fit of the test.
However, market capitalization of shares, the size of the financial market and Fiscal Freedom are confirmed to be positively related to GDPgro, although only singularly and not jointly. Surprisingly, inflation was found to be significant and positively correlated with GDPgro, which is at odds with economic theory. In conclusion, for developed and developing countries the rate of GDPgro shows that both categories of countries were negatively affected by the financial crisis and presented lower rates of growth.
Results in full-fledged model
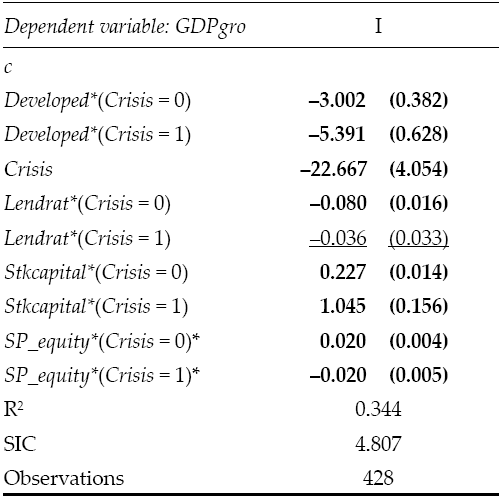
The full-period model is built by introducing interaction variables and using the binary variable Crisis to compare the coefficients of the two periods. The results found match the previous analysis: the rate of growth is higher for developing countries than for developed ones and this holds both in the pre-crisis and post-crisis period; the overall rate of growth is significantly higher in the first period than in the second; the binary variable presents an exceptionally high coefficient, leading to the conclusion that it is indeed responsible for the previous result; moreover, its effect is significant both when used singularly and when interacting with the remaining variables; the negative impact of cost of capital is evident only in the pre-crisis and not in the post-crisis period, while the relationship ruling SP_equity, Stkcapital and GDPgro maintains its significancy (although SP_equity in the second period exhibits a puzzling negative sign, not confirmed by the similar variable Stkcapital).
Trade-off (full period)
To conclude the empirical part, it was fundamental to include a section showing the comparison of financial markets and the productive sector and their effect on growth within the full period of time. This was accomplished by running a regression differentiating the countries sampled in developed and developing (using the once again significant binary variable Developed); however, the results employ data belonging to the full period, underlining the general validity of the findings in Table 6.
Table 6: Trade-off (full period) estimations
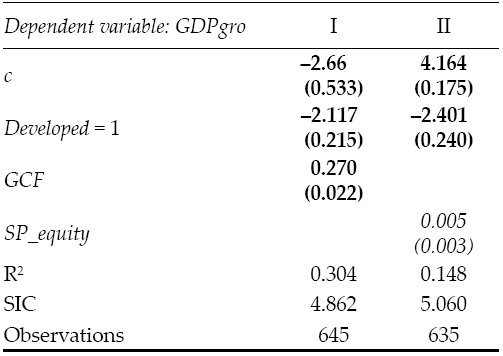
Note: bold: significancy < 0.01; underline: significancy <0.05; cursive: significancy < 0.10.
Source: Own elaboration.
Gross Capital Formation (proxy for the return on the productive sector) and SP_equity (representing the return on investments in the financial system) contribute to determine the overall level of growth; however, the goodness-of-fit in Column I is more than twice the size of the second test, pointing at the chief role of this sector in global economy.
Conclusions
Real and financial sectors are linked as proved throughout this research. The link takes place within the existing tradeoff between marginal product of capital and capital yield, so if capital yield is higher economic growth will decrease and exactly the opposite will occur if marginal product of capital is higher than capital yield. Therefore, economic growth will fall if unemployed resources are allocated towards financial sector, this is not new but in order to avoid economic growth rate from decreasing financial regulation can take place as a capital yield tax. For macroeconomic equilibrium to be guarantee, capital yield tax needs to be applied only when marginal product of capital is lower than capital yield. Financial government regulation inhibits lender agents to permanent keeping resources in financial sector and so prevents economic growth from falling.
On the other side, an excessive high capital yield tax above real revenue will generate lender agents to not be producing in the next period since they will be needing to direct resources on paying taxes. Consequently, an optimum behavior of capital yield tax is determined so allows maintenance the equilibrium growth rate because both productive sectors participate in economic activities. Government regulation is important since corrects negative effects of financial system on real economy and does not generate any other distortion on the economy. In other words, the economy returns to a sustained balanced growth path with full employment because of capital reallocation.
The theoretical results match with those obtained from empirical evidence when financial inefficiency appears and affects negatively on growth, or financial regulation inhibits this negative impact. The main condition to assure economic growth is for marginal product of capital always to be higher than its financial yield. Empirical evidence also shows that there is a negative impact on growth due to shocks from the financial system, highly returns from stock markets decreases the economic growth rate and government regulations to the financial system can inhibit negative impacts on growth.
This analysis allows verifying that there is a linkage between real economy and financial system and that a well-functioning of the latter encourages growth. About the analysis, it is important to say that results depend on the assumptions set out throughout all the investigation; that´s why to extend it is relevant. In this way, the pending agenda indicates that the effect of international financial system (open economy) on growth must be modeled, to expand the role of government in economic activities by introducing consumption and income taxes and verify effects on growth also is necessary, finally to introduce financial instruments such as options, forwards, etc., into financial system is mandatory as well, when concerning the theoretical part. Of course empirical evidence must fit the latter.











 nueva página del texto (beta)
nueva página del texto (beta)