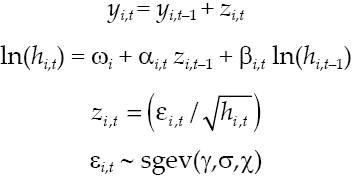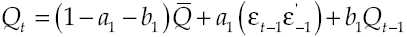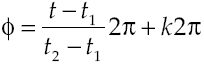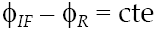JEL Classification: C22; C63; O13.
Clasificación JEL: C22; C63; O13.
Introduction
The fall in the oil prices in 2014 decresed dramatically the average price of energy measured thruogh the Fuel Energy Index1 (FEI). A couple of years before, the Food Index2 (FI) began its declination, briefly interrupted by an increase from March 2016 until August 2016, almost on the same date and with a similar pattern. Morever, the Fat and Oil Index3 (FOI) began its downward movement in the same since 2014. With these facts, it seems that there is not a direct relation between the agricultural foods and the energy prices or the oily cereals and energy prices. In fact, some recent studies as those published by Zhang et al. (2010), Gilbert (2010), Ajanovic (2011), and Qiu et al. (2012) provide empirical evidence of a no linear relationship between food and energy prices.
On the other hand, other studies as those from Kristoufek, Janda, and Zilberman (2013), Vacha et al. (2013) and Nazlioglu, Erdem, and Soytas (2013) found nonlinear relations among the energy, the biofuels, and the food prices. Evenin non-completely developed countries as Turkey, Nazlioglu and Soytas (2011) obtained an alike conclusion. In a similar direction, the studies from Harri, Nal-ley, and Hudson (2009), Ciaian and d’Artis (2011b) or Pokrivčák and Rajčániová (2011) found a long run relation by using cointegration analysis among the prices of some oily cereals, biofuels, and oil prices.
This paper will show that there is a non-linear relation between the yields (returns or growth rates) of the food prices, the biofuels usage, the economic activity, and the energy prices. The main claim of this paper is that the global economic activity that uses energy causes the rise in the prices of fuels (biofuels and liquid fuels4 as substitute goods) and the food (as a competitive good with biofuels). The mechanism begins with those economic activity that need fuel. The vast majority of the business requires machines or transport, which is closely related to the fuel usage.
When there is a business cycle expansion, the price of liquid fuels (closely related to the cost of energy and crude oil) rises, making profitable the production of biofuels. The economic expansion also makes that a greater part of the population consumes more and better basic goods as food (raises the cereals and meat consumption) making the food more expensive because of the demand rising and the increase in the production costs (transport and fertilizers).
The size of temperature variation (measured in the mean world temperature, MWT, variable) were part of the econometric model, but they were statistically non-significative. This variable was kept for the phase synchronization analysis althuogh only presented a single and not related cycle. Also the prices of wheat, corn and oil were redundant to the econometric model (with the associated econometric problems) because there is a variable resuming their prices (Food Index), so they were also discarded from the analysis.
This investigation will use a multi-varied student t distribution of a Dynamic Conditional Correlation model (DCC) and a generalized extreme value distribution for the variance process. Also, this paper contributes to the analysis of the long-run relation among those variables by detecting the number of cycles and the time periods in which they are intimately related (hooked), this is a result of a phase synchronization study.
With the aim of explaining the puzzle of the non-constant relation between these prices, authors as Saitone, Sexton, and Sexton (2008), Ciaian and d’Artis (2011a), and De Gorter and Just (2009) proposed theoretical models that attempt to explain the effect of the energy prices on other relevant variables. In general, the models take into account the role of biofuels (as a competitive product), the land (as a resource for the biofuel) and the food (as substitute use for the land), among other distinctive features that distinguish one model from other. As a general result, this kind of works proved that the use of biofuels would not threaten the food production only if the crops aimed for biofuels come from marginal lands, the producers use second generation technology5 for generating the fuel, or if they use new lands for agriculture. If this is the case, several studies as those from Von Blottnitz and Curran (2007), Pimentel and Patzek (2008) or Hill et al. (2006) point out the fact that the biofuels loose their alleged carbon neutrality6.
A step forward in that kind of models is the use of Computable General Equilibrium models as those proposed by Kretschmer and Peterson (2010), Birur, Hertel, and Tyner (2008) or Hayes et al. (2009). This kind of models gives a very useful theoretical knowledge of the problem, its transmission channels and the possible sources of non-linearity; however, they offer a poor predictive power because of their need for calibration and lack of adaptative response when the economic conditions change.
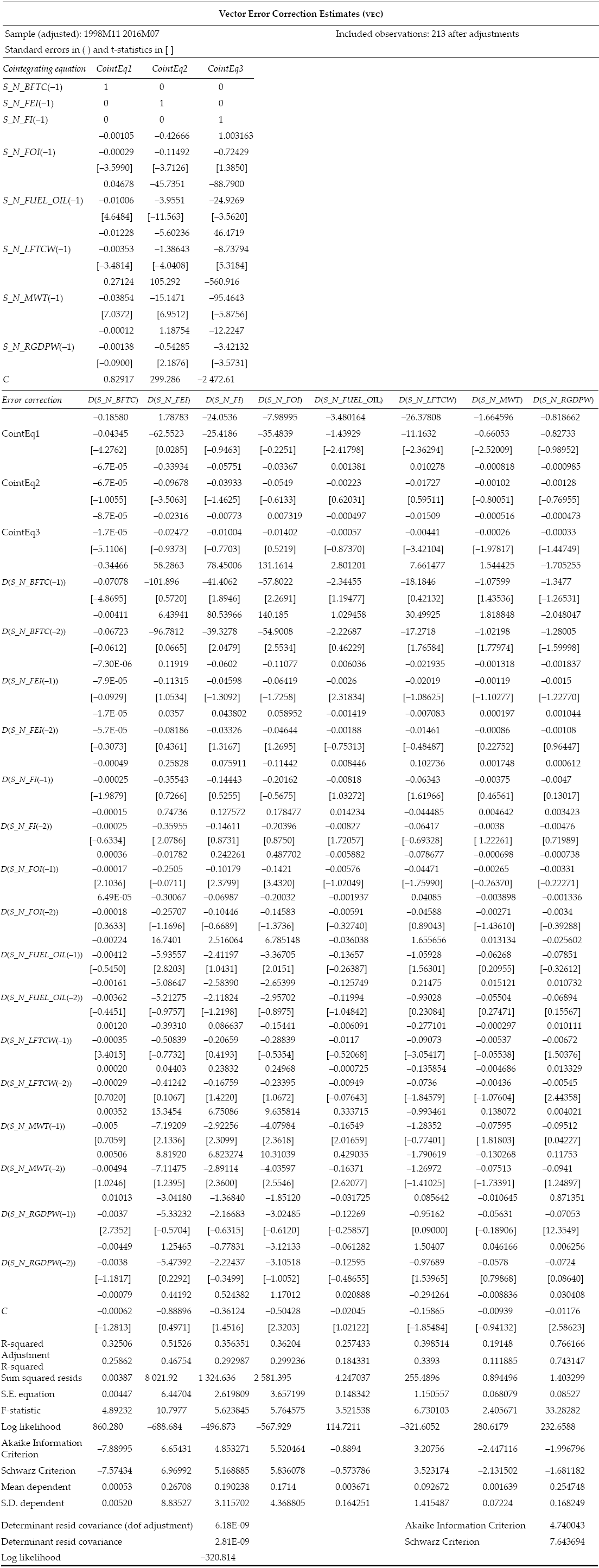
To overcome the problems of adaptation to the variable economic conditions, researchers as Busse, Brümmer, and Ihle (2012) propose non-linear tools as the Markov chain models to explain the regime shift in the relation of the studied variables. Another example of this kind of proposals is the work of Balcombe and Rapsomanikis (2008), they proposed a non-linear Vector Error Correction model (VEC) to explain deviations of the analyzed variables from a long run equilibrium. For their part, Du, Cindy, and Hayes (2011) proposed a similar approach, focused on volatility, using an Stochastich Volatility Merton Jump model (SVMJ).
On the other hand, Escobar et al. (2009) calculated that the biofuels production is only profitable in the European Union when the oil reaches 75 to 80 USD per barrel. They also fund that bioethanol and biodiesel are profitable when the crude oil reaches 90 to 100 USD per barrel. They extended their analysis to the second generation biofuels finding that biodiesel would be profitable only after the crude oil reaches 150 to 160 USD per barrel.
For the United States case, the break-even point for an average bioethanol producers is near to a price of 40 to 50 USD per barrel of crude oil. By their side, an average bioethanol Brazilian producer can be profitable when the international price of the crude oil is near to 30 to 35 USD per barrel and in 60 USD for biofuels derived from vegetable oils.
Whit this information from the current state of the art at hand, this paper states two main contentions: First, the transmission mechanism between the yields of economic activity, the crude oil price, the biofuels price and the food prices (including oilseeds) is nonlinear, nonnormal and changes as the variables evolve. In particular, the correlation of their variances increases as the variance or the mean yield increases. Second, the conditional and nonlinear transmission mechanism present in the yields results in a long run dependence between the analyzed variables. This long-run relation creates economic cycles that can be “hooked” for specific and measurable time intervals that reflect “temporary common trends” for the variables.
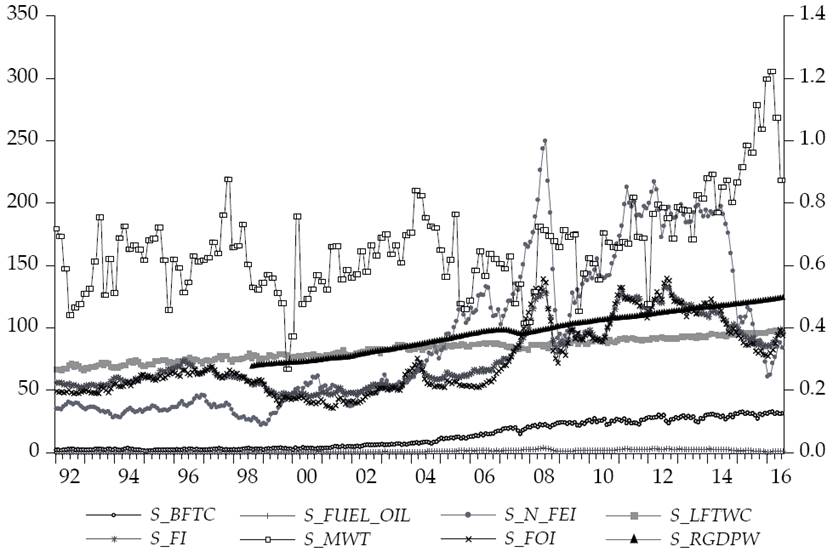
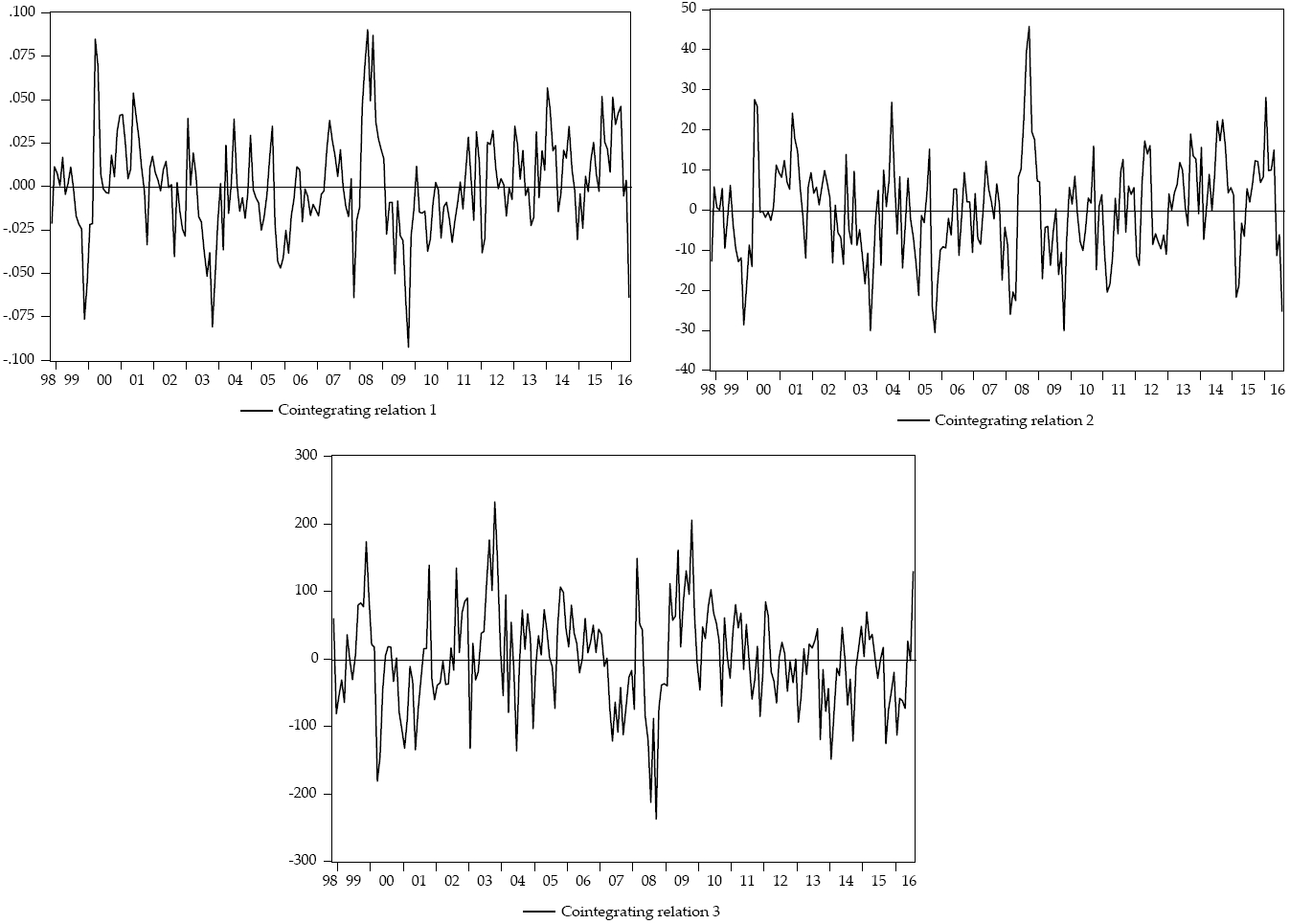
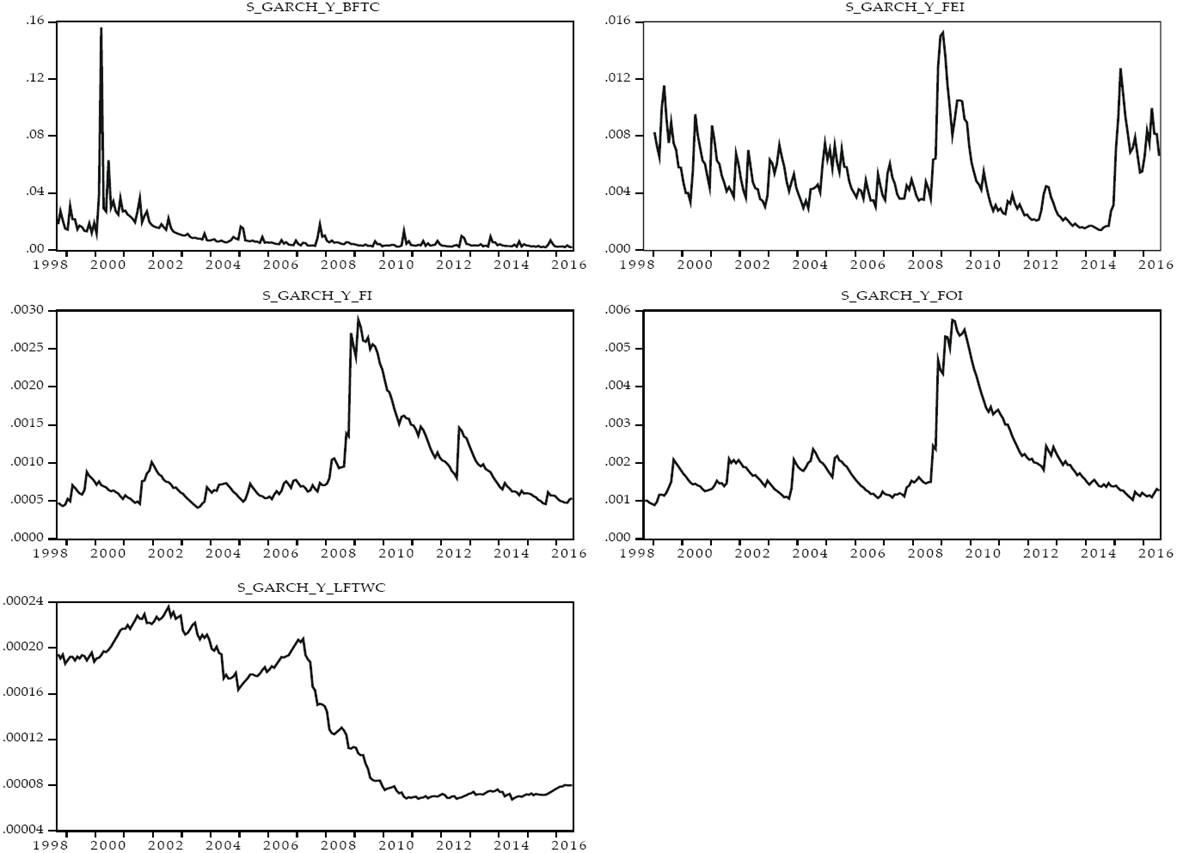
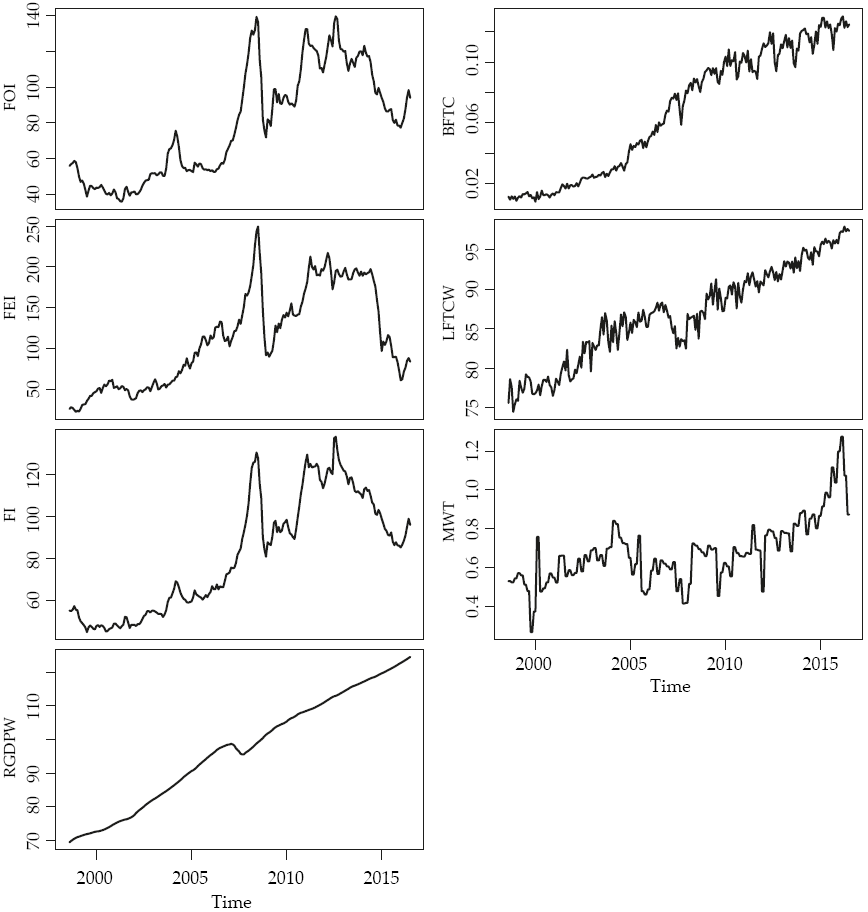
This research proposes a two-fold analysis. The first stage consists of a non-normal Dynamic Conditional Correlation for the yields (returns or growth rates) of the studied variables. The second stage consists of a phase synchronization analysis to the levels of the same variables. For simplicity, we define the studied variables in Table 1 and show its general behavior in Figure 1.
Table 1: List of studied variables and their sources

Note: All of them are available from <https://www.quandl.com/>.
Source: Own elaboration in R (R Core Team, 2015).
Figure 1: General behavior of the analyzed variables
In the next section, this research briefly explains the usage and limits of the dcc model and show the results of its application to the analysis of the volatility transmission between the yields of economic activity, the yields in the prices of the liquid fuel, the biofuel prices and the food yields. In the third section, a similar scheme is used to explain the long run relation and its time duration of the levels of those variables by using a phase synchronization methodology. This method work without making any assumptions on the distribution or stability properties of the time series. Finally, the paper resumes its findings and recommendations.
Dynamic Conditional Correlation model
The Dynamic Conditional Correlation model, DCC, is a multivariate Generalized Autoregressive Conditional Heteroskedasticity model (GARCH) capable of calculating time-varying covariances for the variables in the studied system, as stated in Engle and Sheppard (2001). The DCC was developed by Engle (2002) as an enhancement of the Baba-Engle-Kraft-Kroner model (BEKK), initially proposed Baba et al. (1990), but developed in Engle and Kroner (1995). This model has the shortcoming of needing k 4 parameters to capture all the possible dependence within the model. This makes it unpractical for models above or equal to three variables. Because of that, the model is usually calculated using the principal diagonal of the variance-covariance matrix, thus, it requires the calculation of k 2 parameters.
The DCC model proposed in this paper assumes that the yields, y it , of all the used variables follow a conditionally multivariate student t distribution with zero mean and time-dependent variance-covariance matrix. Thus, the representation of the system y t , is:
In this case, D
t
is the square diagonal matrix of time-varying standard deviations from the univariate generalized extreme value distribution (sgev) for each EGARCH models. Nelson and Cao (1992) supposed for each variable,
where sgev (γ ,σ, χ) are the parameters of location, skew, and shape, respectively, for the generalize extreme value distribution of the innovations in each yield.
To express the dynamic correlation structure, the model postulates that it depends on the squared errors of the system
In this case,
In their papers, Engle and Sheppard (2001) and Engle (2002) demonstrate the estimation procedure for the parameters and their consistency, so all the common set of hypothesis tests can be performed to check if the system’s residuals are white. If after performing those tests, the residuals result to be white noise (independent and jointly normal), then the model explain the phenomena and so, it took out all the dependence structures of the system.
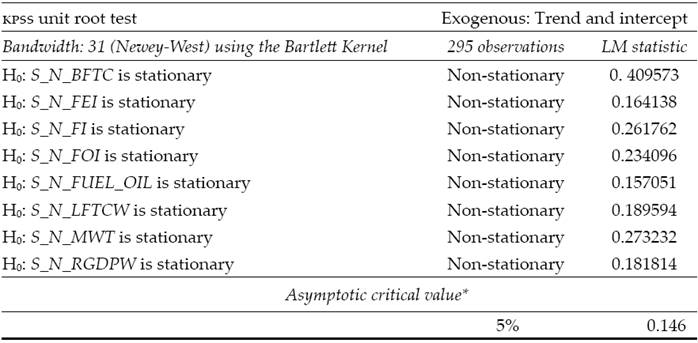
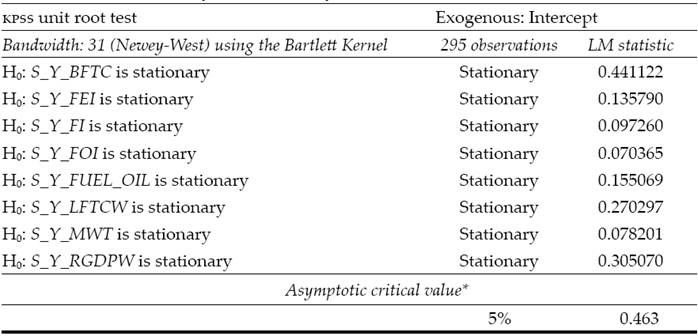
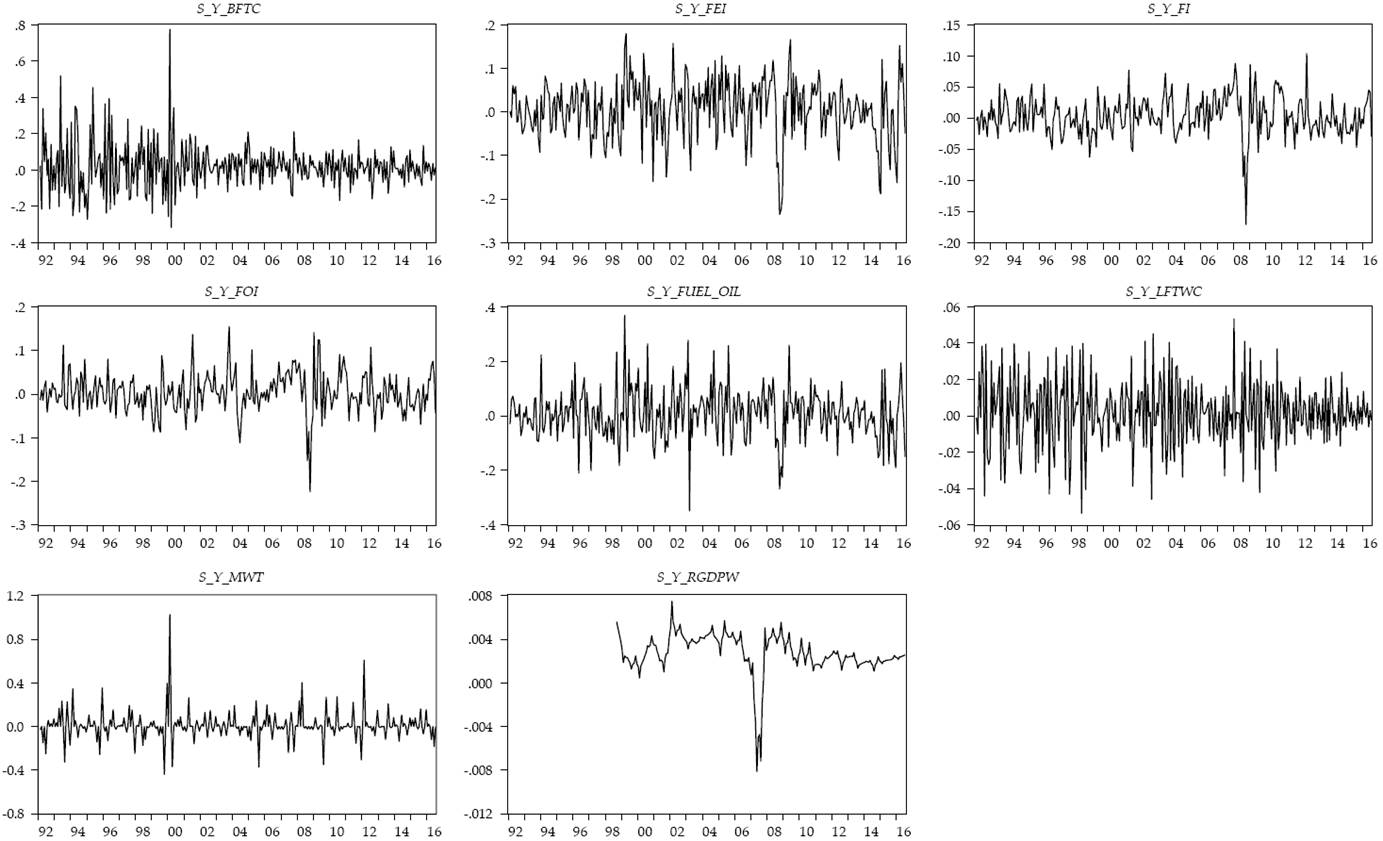
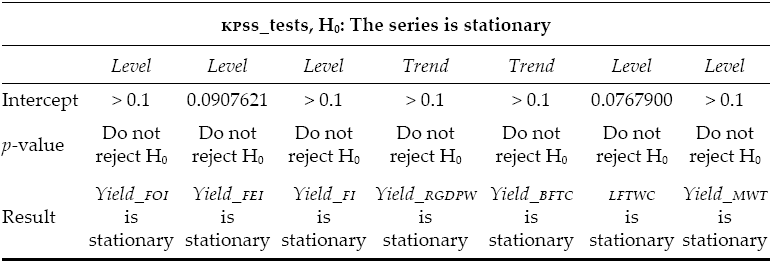
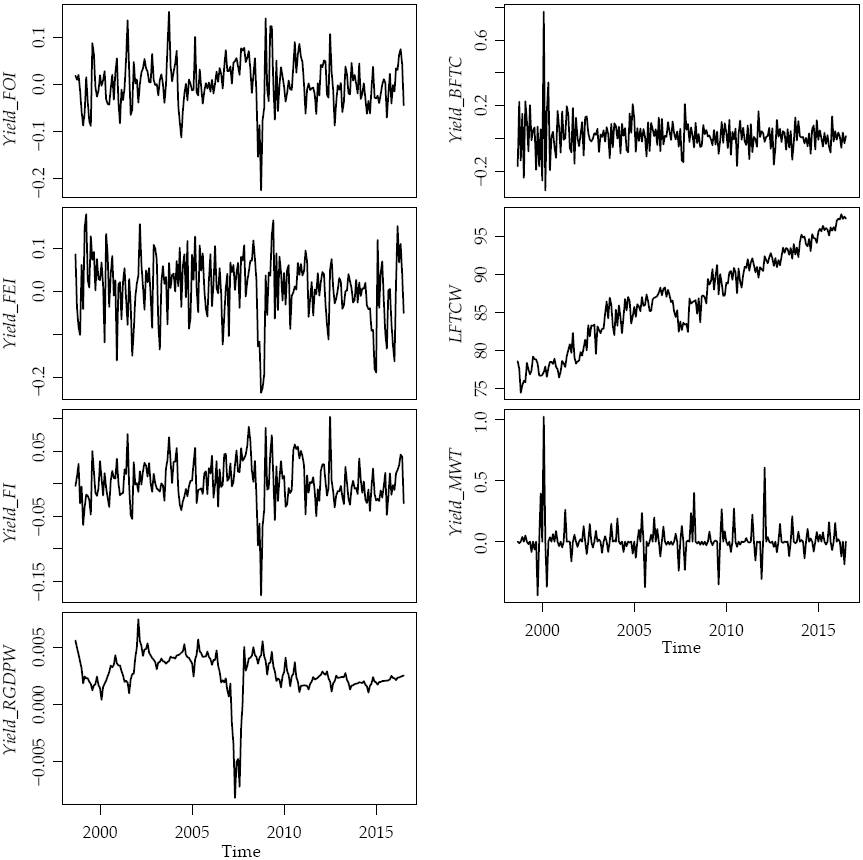
Now, after briefly explaining the dcc model, we present the results of the dcc model applied to the proposed system. Table 2 shows the results of the Kwiatkowski-Phillips-Schmidt-Shin test (KPSS) (Kwiatkowski et al., 1992) for the yields of the selected variables7 and Figure 2 shows the general behavior of the yields of the selected variables.
Table 2: KPSS tests for the selected variables
Source: Own elaboration with tseries package (Trapletti, Hornik, and LeBaron, 2016) form (R Core Team, 2015).
Source: Own elaboration in R (R Core Team, 2015).
Figure 2: General behavior of the yields of the analyzed variables
As the reader may see, the FI, FEI and FOI index yields have very similar behavior. They are also heavily related to the yield of the RGDPW. On the other hand, there seems to be a likelihood between changes in the abnormalities in the MWT and the use of BFTC, but the relation is statistically nonsignificant.
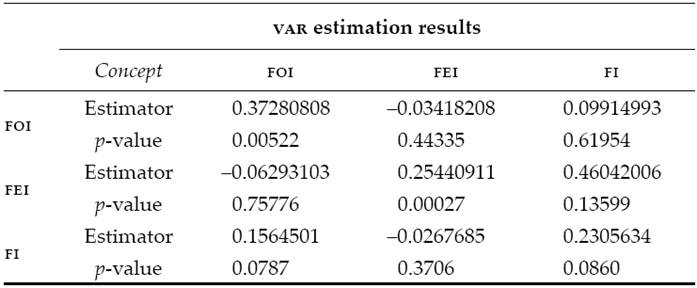
To properly compare this work with those cited in the introduction, the paper shows a Vector Autoregressive model (VAR) in Table 3. In this table, the reader may see that there is no evidence for supporting the hypothesis of linear dependence between the yields of Fats and Oils, Energy or Food indexes. In order to maintain the article length acceptable, the paper does not present the impulse response graphs, nor the residuals test or the variance decomposition graph for the model. As the reader can anticipate, they only show almost non-related patterns and nonlinearity problems, as a significant part of the previous authors showed.
Table 3: VAR model for the Fats and Oils, Energy and Food indexes
Source: Own elaboration using the vars package (Pfaff, 2008) in R.
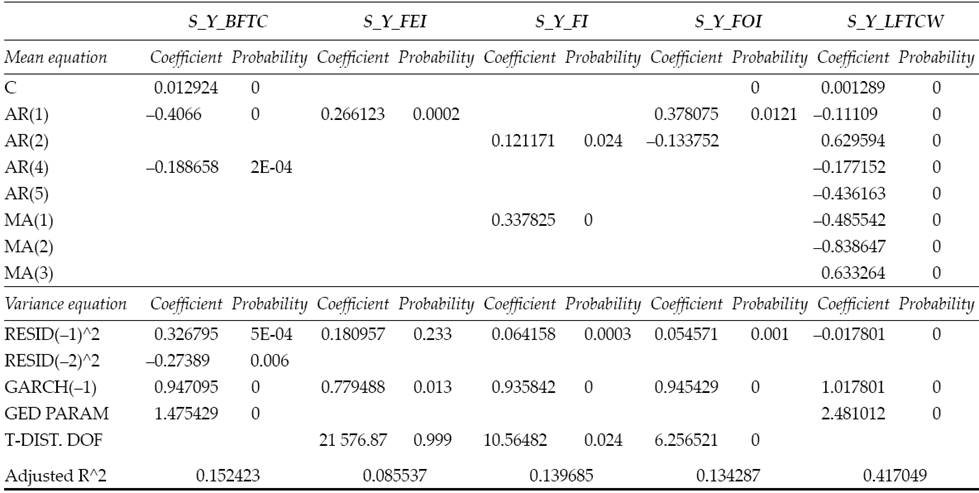
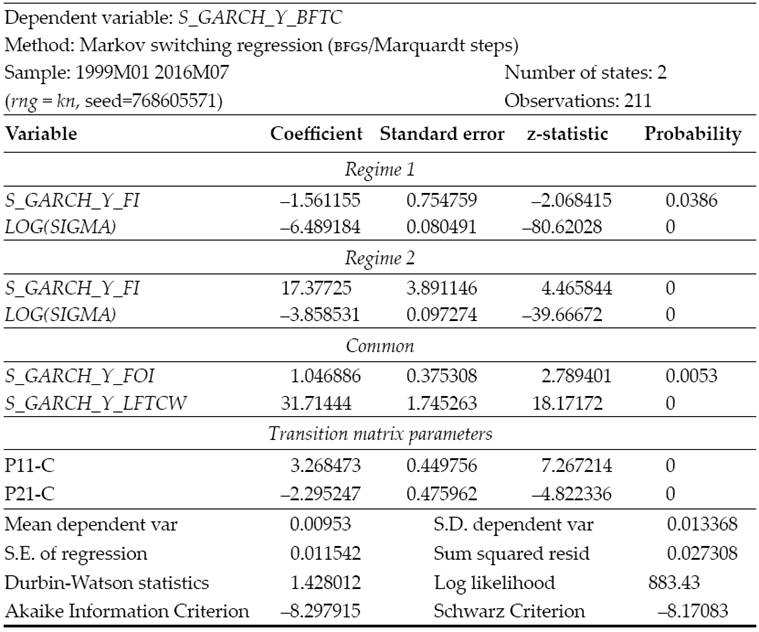
In an attempt to catch the nonlinear relations within the proposed system, the paper exhibits a DCC model, done using the rugarch (Ghalanos, 2015a) and rmgarch (Ghalanos, 2015b) with R packages. The dcc model appears in Table 4.
Table 4: DCC model for the proposed system
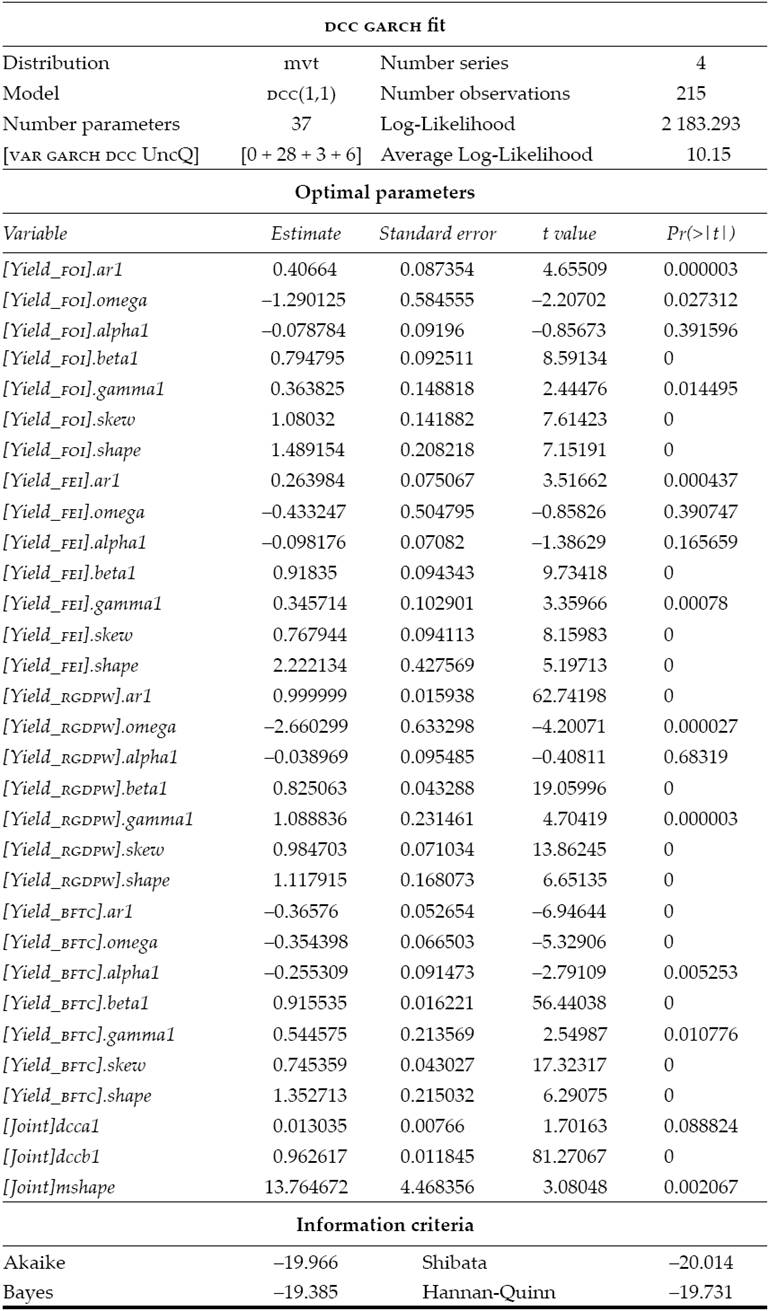
Source: Own elaboration with the rugarch (Ghalanos, 2015a) and rmgarch (Ghalanos, 2015b) packages for R.
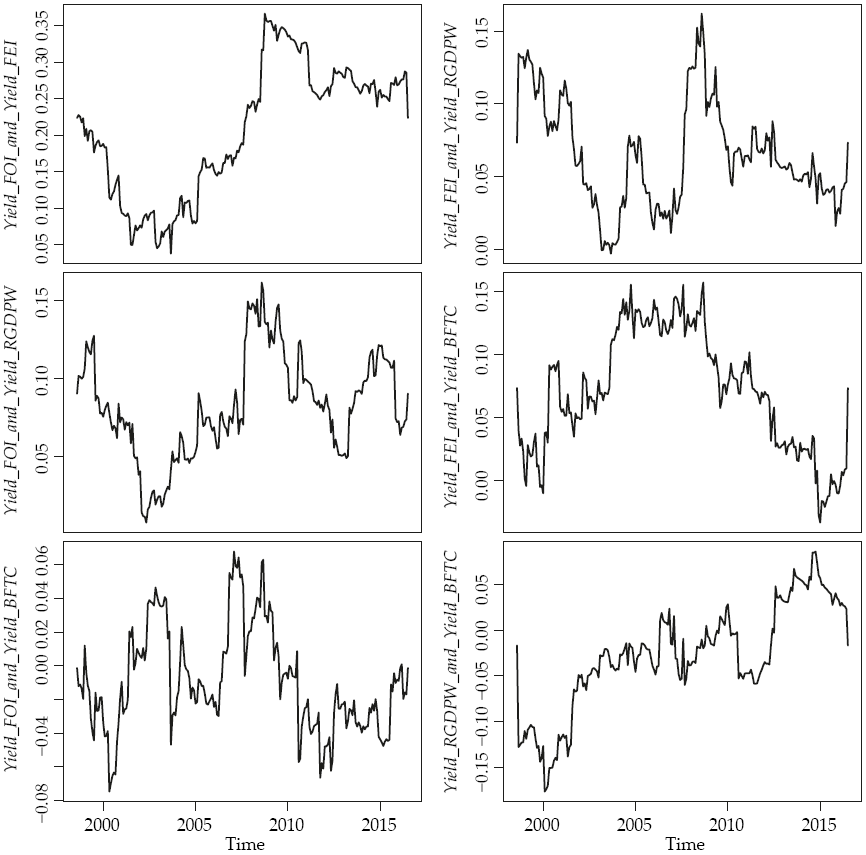
The main result of this part of the article is showed in Figure 3. There, the reader may see the way in which the correlations among the variables change over the time, peaking during 2008 (when the food prices rose sharply) and getting down to the growth of the world’s GDP stopped and recovered as the world’s economy gets recovered.
Figure 3 also showed the “Markov switching” feature described by other authors. In fact, the graph shows correlations swinging into a large but related correlation spans. This related correlations spans are also the footprint of the volatility clusters and other nonlinearities registered in other works. This characteristic also may explain the nonnormal distribution that affects the econometrics calculations given by previous works.
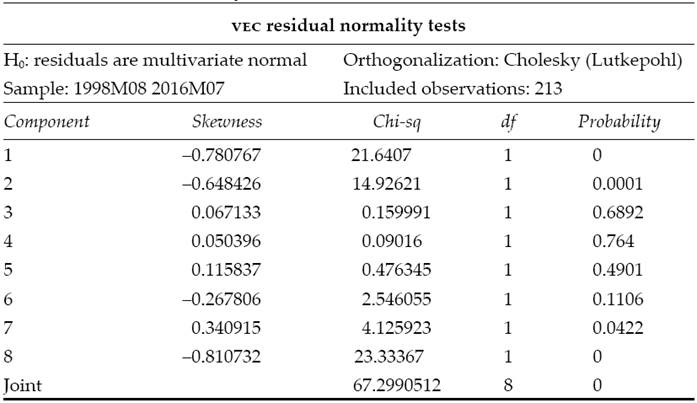
Unfortunately, the examined system is heavily nonnormal and even though the dcc model takes out the first and second order dependence structures, there are higher order dependencies that prevent the model’s residuals from reaching normality nor independence. In Table 5 and Table 6, we show the joint normality test (Henze and Zirkler, 1990) and the Brock-Scheinkman-Dechert (BDS) test (Broock, Scheinkman, and Dechert, 1996) for the model residuals.
Table 5: Multivariate normality test for the model’s residuals

Source: Own elaboration using (Korkmaz, Goksuluk, and Zararsiz, 2014) MVN package from R.
Table 6: BDS test for DCC model’s residuals
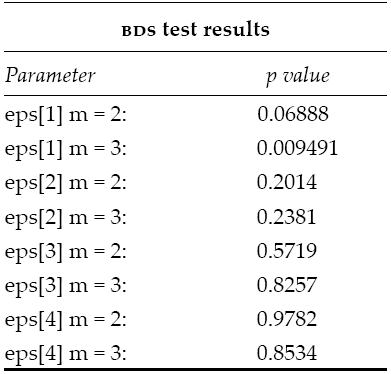
Source: Own elaboration with (Wuertz, 2013) fNonlinear package from R.
After performing all the necessary tests to the dcc model, the reader may see that it does not suffice to get white noise residuals. Nevertheless, the model captured the first and second order dependencies from the specified system and helped us to prove the first part of the paper’s arguments:
There are nonlinearities in the system, and the yields cause them in the World’s GDP, they pass to the Fuel and Energy and Fat and Oil indexes and then to the Food Index.
The volatility spillover occurred when the whole system becomes stressed.
Now, the paper presents a phase synchronization analysis to the levels of the same variables to test similar relations in original series without making any assumptions on the distribution or the stability of each time series.
Phase synchronization
The synchronization is used to assess the similarity between two nondeterministic systems. Christian Huygens created the concept when he discovered that two pendulum clocks tend to synchronization if they were on the same surface. This type of synchronization was called “phase synchronization” and originated the coupled oscillators analysis. The main characteristic of this kind of systems is that no matter how wide the pendulum may be, or if they are of a different size, the will fulfill their cycle at the same time.
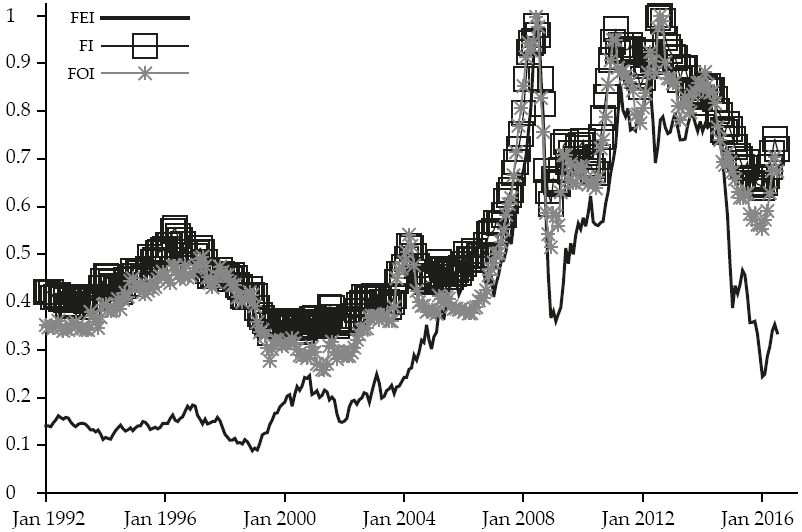
This type of phenomenological analysis can be used to analyze systems that hardly meet the standard assumptions of independence and joint normality that are common in the time series analysis, as those of this paper. The first step to perform this analysis is to normalize (get into a similar scale) all the time series. For this purpose, all the time series are divided by their maximum, the result of this procedure appears in Figure 4.
Source: Own elaboration with Fortran and GNUplot.
Figure 4: Normalization for the main Food and Energy indexes
The main objective of using this kind of methodology is to the obtain the system dynamics and to get the time periods in which the cycles of the series had the same duration and therefore are synchronized. It is important to mention that this synchronization does not mean that the dynamics of the series are in the same direction, it only implies that the cycles are of the same length. As the reader may see in Figure 4 the dynamics of the FEI, FI, and FOI indexes seem to be synchronized.
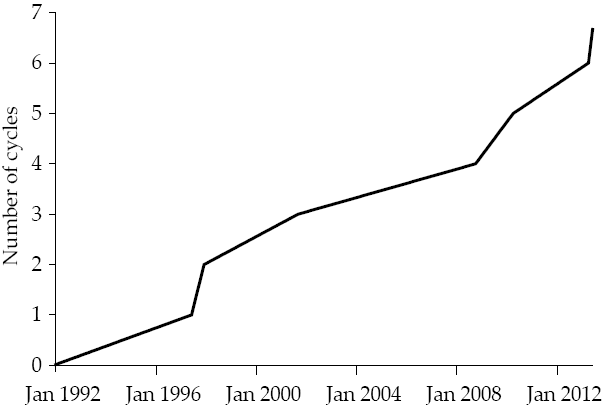
The synchronization analysis continues with the definition of the cycles of the smoothed time series of the first derivative. The period in which the smoothed series presents two sign changes defines the entire cycle8. In the case of random time series, the duration of the cycles may be different for each cycle, so the first step is to determine how many cycles presents each time series. The article shows this calculation for all the time series in Table 7.
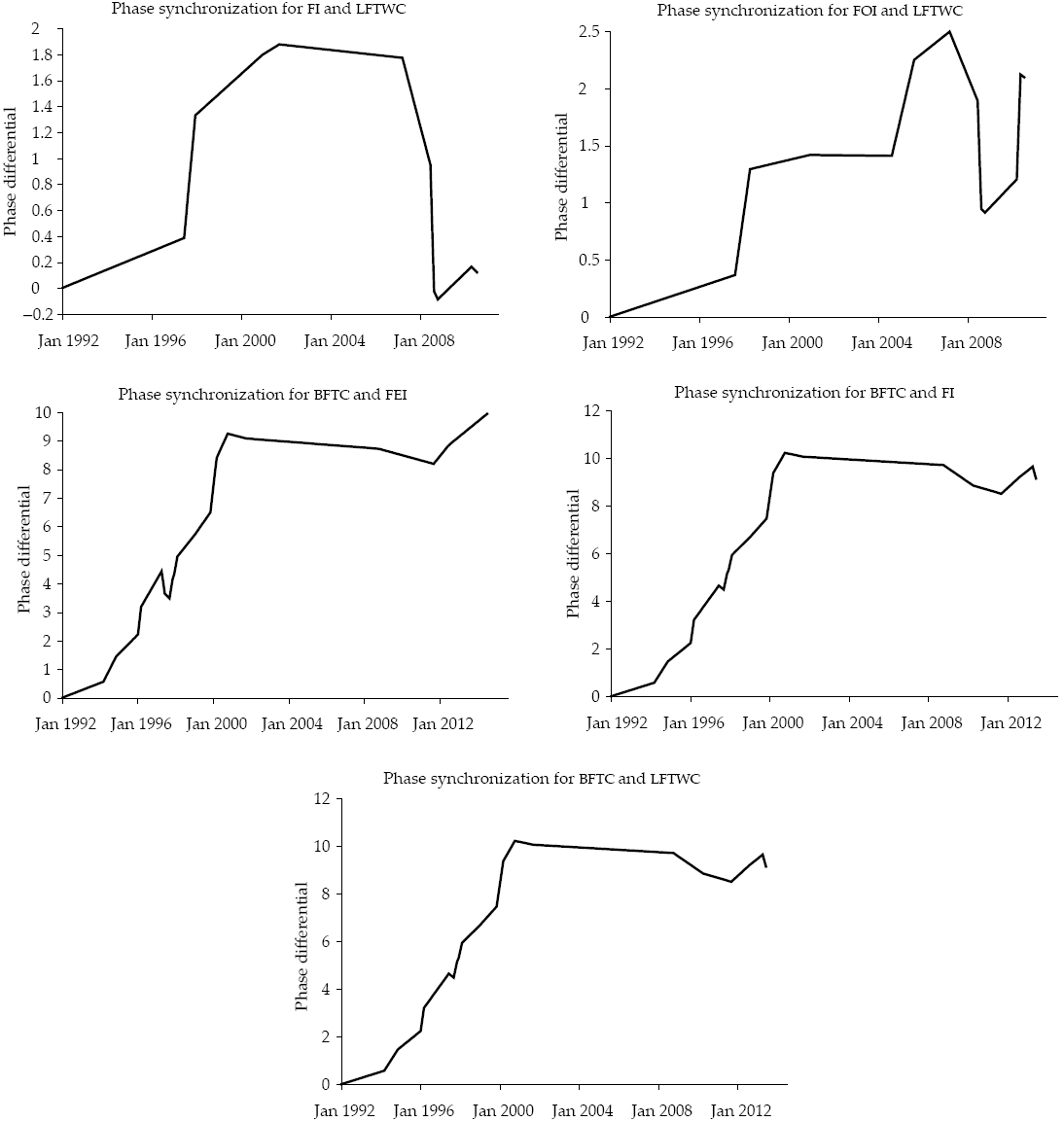
The above table provides empirical evidence of the visual analysis stated with Figure 4. Table 7 provides empirical evidence that FEI, FI, LFTWC and FOI present similar trajectories, with almost equal number of cycles (FOI is faster and LFTWC slower).
Figure 5 shows the time in which each variable completes its cycles. It is re-markable that in October 2008, the FEI, FI, and FOI indexes ended their cycles in the same time (LFTWC did it a few months earlier). A similar phenomenon (but not so accurate) occurred in 2012 for FEI and FI, with FI and FOI in 2010, and with FEI and FOI in 2014.

Source: Own elaboration with Fortran and Excel.
Figure 5: Short run cycles for the selected variables
It is also remarkable that FEI and FI indexes have a very similar number of cycles, but their amplitude (distance from peak to peak) in the 2008 cycle were different. In this case, the FEI index has an amplitude of 212.48 and for fi is just 83.85 while FOI has a similar 86.79, this is an empirical evidence of the series being “hooked” in stress periods and may remain independent under other conditions. The goodness of this kind of analysis is that it seeks synchronization in the dynamics of the series, this is the generated number of cycles not in the amplitude.
Once the number of periods is known, one may calculate the phase for each variable. The phase is the amount in which each oscillatory cycle increases 2π. It can be calculated using:
where k is a counter for the cycles9. The only change will be the number of the cycle, k. Applying the phase equation to the analyzed data, we obtained a phase graph like the one obtained for the Food Index and showed in Figure 6.
The empirical analysis revealed so far by the series only refers to its individual properties (number of cycles and its amplitude); however, to determine if there is synchrony between the dynamics of these variables is necessary to calculate the phase differential. If the phase differential is constant, then both series present a phase synchronization, this is:
The constant difference between the phase of two-time series implies that the duration of the cycles is the same for both, although their respective intensity (amplitude) is not. In Figure 7 we present a differential analysis for the FEI and FI time series. The research uses this time series as an example because those series presented the same number of cycles. In Figure 7, the reader can observe that the phase difference is almost constant, with a first synchronization period from January 1992 to August 1998, and a second term from September 1998 to March 2008 when the series lost their synchrony.
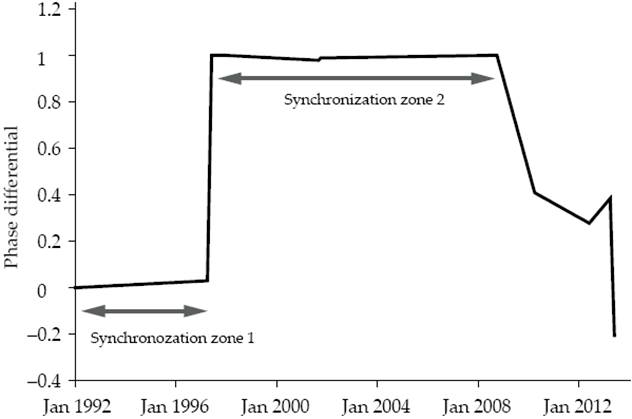
Source: Own elaboration with Fortran and GNUplot
Figure 7: Phase differential for Fuel an Energy Index
Figure 8 shows a resume of the phase synchronization of the selected variables. Here, the reader can observe that the whole system presents an almost constant phase synchronization since 2000 (when the biofuels became popular)10. The reader also may see that the phase synchronization is partially lost when the world’s economy faces a crisis. The loss of synchronization is acuter in the Liquid Fuel Total World Consumption and Biofuel Consumption.
Source: Own elaboration with Fortran and GNUplot.
Figure 8: Resume for phase synchronization for selected variables
It is also remarkable the fact that is the Liquid Fuels Total World Consumption, and thus the economic growth the leading factor of the system and not the anomalies in the global mean temperature, MWT. The lack of phase synchronization of the anomalies of the global average temperature indicates that the shock does not come from the global agricultural sector (it is not so decisive for the Food Index if there are some anomalies in some parts of the world). A possible explanation for that behavior is that a bad agricultural season in a country is partially offset by a good season elsewhere, also because the market prices control the amount of resources used for energy and food as the rest of the economy plump or fall.
Conclusions
This paper gave empirical evidence of the existence of an economic system that includes the Biofuel Total Consumption, BFTC; the Liquid Fuels Total World Consumption, LFTWC; the Food Index, FI); the Fuel Energy Index, FEI, and the Real Gross Domestic Product for the World, RGDPW, by using a DCC model and the phase synchronization methodology.
The paper also showed with the DCC model that is the RGDPW, and not the MWT the variable that unchains the movements of the whole system. The transmission mechanism starts with the RGDPW pushing up the LFTWC and thus its prices (FEI). When the prices are high enough, the production of biofuels becomes profitable, and its consumption (BFTC) rises, this makes the oily cereals (FOI) more expensive and with them the whole food chain (FI). The effect on the food prices stays until the world’s economy become into a slower growth or a recession, causing the apparent disconnection of the system.
The phase synchronization methodology showed that the apparent disconnection is just over a part of the system, but that the mechanism remains latent. It also demonstrated that this mechanism is present since 2000 when the biofuels began to be popular and remain untouched even when there are temperature anomalies (MWT).
The last argument does not attempt to be a reason for stopping worrying about the planet and the consequences of the human activities over it. On the contrary, it is a warning about the “perfect storm” that we can face if the global economic activity is rising (especially in densely populated areas), there are bad harvests due the climate change in a cereal producer country and the cereal commerce is banned or restricted (as in 2008). In this scenario, all countries will need some local food and grain production or long run commercial agreements with trustable partners to use the market mechanisms to control the sure in the food prices.
The paper also demonstrated that the nonlinearity of the problem comes from the “production switch” given by the energetics prices over the biofuels, the volatility clusters on the grains and energetic markets and the lags on the transmission mechanisms. The existence of substitute goods for energetics and the time in which the food market responds to the changes may be the cause of that lag.
Finally, the paper gives some indirect evidence about the markets ability to handle the disequilibria in the energy-food system through the price mechanism. It remains as a possible line of research the temporary effects of this adjustment mechanism to the poverty and the energy industry.











 nueva página del texto (beta)
nueva página del texto (beta)