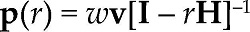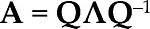The idea of natural prices is one of the oldest and most important concepts in political economy. Natural prices were used by the Physiocrats but only got fully constructed by the classical political economists and Marx. In more recent times, they were further developed by Piero Sraffa and several political economists inspired by his work. Modern Classical Economics and Reality by Theodore Mariolis and Lefteris Tsoulfidis constitute an important contribution within the latter tradition.
All these authors think of natural prices as the center of gravity around which market prices, or prices observable in the economy, gravitate as the result of forces of competition between commodity producers. However, its use has served different purposes throughout the history of economic thought.
For classical political economy, natural prices is an essential element in the explanation of how capitalist societies determine their division of labor. To explain this phenomenon, political economists developed the long-period method, i.e. a set of abstractions to explain the self-organizing character of decentralized societies that meet their needs by producing for exchange (Foley, 2013 and 2016). These abstractions are composed of a commodity-producing society with free mobility of capital and labor across lines of production. Within this framework, the capitalists’ search for the highest profit incomes per amount of capital advanced generates a competitive process that produces a series of linked emergent outcomes: a capital distribution across industries, a set of natural prices and an average profit rate arising from the equalization of individual profit rates. The emergence of an average profit rate implies that profits tend to be earned in proportion to the amount of capital advanced, independently of how the composition of this capital is divided between labor and means of production outlays. The resulting distribution of capital across industries together with the average labor requirements per capital in each industry determines society's division of labor. These natural prices, which allow the equalization of profit rates across industries, are called prices of production. Differences between market and production prices generate profit rate differentials among industries that produce capital mobility (and therefore changes in the division of labor) in a direction that tends to reduce these discrepancies.
Marx uses prices of production when introducing competition between capitals to his labor theory of value and surplus value. One of his major concerns is to show that industries’ profits, which result from the profit-rate equalization process, are redistributions of the pool of surplus value generated in the whole economy, so that the aggregate profits are equal to aggregate surplus value (Foley, 2013 and 2016).
With a different agenda in mind, Sraffa (1960) proposes a model in which prices of production and the profit rate are simultaneously determined under given methods of production (the combination of means of production and labor in each industry) and income distribution (the functional distribution between wages and profits). The standard representation of this model considers the following price and quantity system with single product industries (no joint production), circulating capital (no fixed capital), homogeneous labor, and uniform wage and profit rates:
where scalars r and w are the profit and wage rates, p(r) and l are the 1×n price of production and labor coefficient (quantity of labor per unit of output) vectors, x and y are n×1 gross and net output vectors, and the n×n matrix A = {aij} is the input coefficient matrix, containing the quantity of the i-th means of production needed to produce one unit of the j-th commodity. The collection of the methods of productions of all industries (l,A) constitutes a particular technique for the economic system.
In this model, the means of production are themselves commodities produced within the economic system in consideration. Being heterogeneous in nature, if we were to aggregate any set of commodities, we would have to aggregate them in value terms, according to their prices of production, which in turn depends on the rate of profit. For instance, the capital used per unit of output in the j-th industry is
One important implication of Sraffa's model is that, under the considered set of assumptions, prices of production, the profit rate and in general, the value of any commodity aggregate could have a considerable nonlinear behavior as income distribution changes, even if the technique of the system (l,A) remains unchanged. For instance, the value of j-th industry's capital κj(r) could increase and then decrease (or the other way around) as the value of the wage rate (and therefore of the profit rate) reduces from its maximum up to zero. This type of behavior poses additional problems to the neoclassical construction of (macroeconomic) production functions and to its theory of income distribution. To see this, consider the profit rate (and not the wage rate) as the given distributive variable. If we take the value of the gross output as the numéraire of the system (px = 1), then we can solve equation [1] for prices of production and the wage rate as:
where v = l[I - A]-1 is the vector of total labor time and H = A(I - A)-1 is the matrix of vertically integrated input coefficients, which gives the total amount of i-th means of production required to produce one unit of the j-th commodity. Equations [3] and [4] represent the price and wage-profit curves, respectively. Equations [3] and [4] could have a considerable non-linear behavior or curvatures in the face of changes in the profit rate. Each technique (l,A) gives a particular wage-profit curve. Hence, theoretically it is possible for the curvatures of the wage-profit functions from different techniques to have multiple intersections among them, implying that one or more techniques be selected from different segments of the profit rate range (if the choice of technique is based on the highest wage rate for a given profit rate). This possibility could generate phenomena like re-switching and reverse capital deepening, which pose additional problems for the construction of production function with neoclassical features of income distribution (like the adoption of techniques more intensive in means of production relative to labor under an increasing r/w ratio).1
Finally, another implication of the possible behavior of prices of production in [3] concerns the relationship between prices and the total amount of labor embodied in commodities v. This relationship constitutes an important element of the so-called debate on the transformation problem.2 Prices proportional to the vector of total labor time v can be derived using equation [3] evaluated at r = 0: p(0) = wv. Equation [3] implies that for a positive rate of profit, prices of production, and therefore market prices, could be considerably different from direct prices vd (prices proportional to total labor time v and where the sum of total labor time is equal to the sum of total prices: vd x = px).
Following Sraffa's developments, since the end of the 1970s an increasing number of scholars have empirically estimated price of production models, the study of which had only been done theoretically before this period. Some of their work calculated prices of production at the observed income distribution and studied the relation between these prices, direct prices and market prices. Other scholars have studied the effects that changes in income distribution have on the relation between wages and profits and on standard prices (prices of production measured in terms of the standard commodity, a composite commodity the value of which does not change when income distribution changes). There are two important results from this broad literature that continues up to now. On the one hand, prices of production, direct prices and market prices are considerably close to each other. On the other hand, standard prices and the wage rate are simple, nearly linear functions of the profit rate. These results constitute a puzzle for the implications derived from Sraffa's work discussed above. As more countries and time periods are studied, more evidence piles up into these type of results.
However, what has only been considered marginally in the literature is the explanation of the empirical regularities in these estimations. What are the economic forces that produce these regularities and what are their corresponding mathematical representations (or constraints) in price of production models? The possibility of 1) experiencing significant curvatures in standard prices and the wage-profit functions and 2) having considerable deviations between direct prices and market and production prices, comes from the possible relationships between industries’ labor, output and means of production (l, x, and A, the exogenous variables in [1] and [2]). Therefore, little attention has been paid to why actual economies allocate labor in such proportions and have such a means of production commodity structure that produces direct prices, prices of production, and market prices to be close to each other. By the same token, why do observed economies have labor and output proportions and an input commodities structure that generates nearly linear behavior in standard price and wage-profit curves under hypothetical changes in income distribution? Theodore Mariolis and Lefteris Tsoulfidis’ Modern Classical Economics and Reality constitutes an important effort to shed light onto this question.
The book's main objective is the systematic study of prices of production and the profit rate in linear production models. It compiles more than 15 years of careful, rigorous and innovative research done by the authors on what they call “modern classical theory of value.” This long-period research project, and its compilation in the present book, includes extensive collaborative results with their master, doctoral and postdoctoral colleagues. This represents a contribution not only in the generation of new knowledge, but also in the formation of a new generation of scholars interested in these relevant topics in political economy.
Modern Classical Economics and Reality focuses on prices of production and the profit rate and their dependence on the technique of production, the wage rate and output proportions, constitutive elements of what the authors refer to as the “core” of the classical theory of value. Of particular interest is the study of how relative prices and the profit rate behave in the face of hypothetical changes in income distribution. This task is based on a rich mathematical exposition of linear production models. There is a considerable effort to identify the algebraic structure of the models and to untangle their properties. The authors study in depth price of production models that only consider single commodity industries and circulating capital, like equations [1] and [2]. However, they also address several variants of this battle horse model, like fixed capital, joint production, the quantity system, etc.
The economic and mathematical material in the book is presented at an intermediate and advanced level and therefore assumes that the reader has a knowledge of price of production models equivalent to Pasinetti's (1977) or Vegara's (1979) textbooks. For some topics, like the different representations of the price and quantity system for n commodities, Mariolis and Tsoulfidis’ book represents an alternative to Kurz and Salvadori's (1995) advanced chapters.
However, Modern Classical Economics and Reality contains a set of features not shared by the previously mentioned classic textbooks and other books on prices of production. These characteristics arise from the series of theoretical and empirical contributions that the authors have produced. Two unique features in this book stand out and make it a mandatory reference for research on the topic.
First, empirical evidence plays a key role in the exposition. The book contains an extensive and systematic account of the empirics of prices of production. It reviews the empirical work from the literature and reports the empirical contributions for several countries and years done by the authors. Most of the presented theoretical concepts have an empirical counterpart. In addition, the authors conduct an analysis on the different empirical results.
Second, and in accordance with the subtitle of the book (A Spectral Analysis of the Theory of Value and Distribution), Mariolis and Tsoulfidis dedicate a great deal of research effort and book space to the theoretical and empirical study of the spectrum of the input matrix and the role it plays in linear production models. The spectrum of the input matrix and its use to make an alternative representation of the linear production models require some lines of explanation.
The spectrum of matrix A is constituted by the set of its different eigenvalues.3 If scalar λ and row and column vectors z and q have a relationship with A as zA = λz and Aq = λq, then λ is an eigenvalue of A and z and q are the left and right eigenvectors of A corresponding to eigenvalue λ. If we assume that matrix A is diagonalizable and for simplicity, that it has n distinct eigenvalues, then it has the following spectral decomposition:
where Λ = diag{λ1,…,λn}, matrix Q has as columns the right eigenvectors {qi}, and matrix Q-1 has as rows the left eigenvectors {zi}. Substituting equation [5] in the price and wage-profit curves [3] and [4], they can alternatively be represented as:
where v* = vQ and x* = Q-1x are the representations of the total labor and gross output vector in the coordinate space formed by the linearly independent eigenvectors {qi} and {zi}, matrix ΛH = Λ(I - Λ)-1 = diag{λH,1,…,λH,n}, and λH, i = λi (1 - λi )-1.
The authors conduct an exhaustive analysis of the estimated price and wage-profit curves and
conclude that observed “single-product economies” like [1] and [2] have low “effective
dimensions”. More specifically, they argue that the observed shapes of these
n×n systems could be well approximated by lower
dimension models: 2×2 for price-profit curves [3] and 3×3 for the wage-profit curve [4].
The main point that the authors wish to highlight is that the “low dimension” of the
estimated price of production systems is connected to the observed low “effective ranks”
of the input matrix H, i.e. a small number of observed
eigenvalues λH
,i
with considerable magnitude and the rest of them clustered around
zero. As price and wage-curves [3] and [4] can equivalently be expressed in terms of the
eigenvalues λH,i and the
The book is comprised of six chapters. Chapter 1 describes how relative prices, the rate of profit, and the value of capital respond to changes in income distribution according to the classical political economists, neoclassicals, Dmitriev, and Sraffa. The authors conclude that results from modern classical thought (Dmitriev and Sraffa) pose conceptual and analytical difficulties to the economic propositions or hypotheses from “traditional theories” (classical, neoclassicals, and Marxian). In the second half of the chapter, the authors present what they call the “state variable representation” of a class of linear dynamic systems and advocate for its adoption to study linear price of production models on the grounds that the former represents the essential dynamic and stationary properties of the latter.
Chapter 2 focuses on the properties of prices of production and the profit rate in systems like equations [1] and [2]. It is important to mention that throughout the book, wages are sometimes part of the capital advanced and sometimes they are not. However, there is no clear justification for this back and forth treatment of wages nor a discussion of the economic implications of this. This chapter presents equation's [1] general characteristics and also particular cases representing hypotheses from different schools of thought. In spite of this emphasis, the chapter also considers more general relative price models and the study of the quantity system (the study of growth and output allocation). There are two aspects that the authors wish to deepen: the existence of upper and lower bounds in price and wage-profit curves as income distribution changes; and the effects of changes in income distribution and total productivity shifts on price-profit curves. The results from this chapter are that price-profit curves could have changes in their trajectory as income distribution changes and total productivity shifts, which would pose potential problems to the hypotheses of “traditional theories”.
Chapter 3 provides estimations and evaluations from the models and propositions discussed in the previous chapters for a variety of countries and years. However, it begins with a simple three industry example (constructed from actual data) which, together with the appendix of the chapter, gives a useful introduction and guide to the realm of empirical research on prices of production. They find the following main results, which are consistent for all countries and years considered within the meaningful profit rate (not too close to its extreme values):
Direct prices, prices of production, and market prices are close to each other.
Price of production-direct price deviations are proportional to the differences between industries’ capital intensities (the ratio of the value of means of production and labor) and economy's average capital intensity.
Price-profit curves are mainly determined by the relative capital intensities.
Prices of production are, in general, monotonic functions of the profit rate (their trajectory is nonincreasing or nondecreasing) in the considered range of profit rate values.
The wage-profit curves are nearly linear.
Price and wage-profit curves tend to behave as a three and two-industry system, respectively.
Chapter 3 concludes also that direct price-price of production deviations are robust across the different measures used to assess their distance. With this motivation, chapter 4 studies the properties of different measures of deviations. They conclude that, for “realistic” values of the profit rate, price deviations tend to be small and that they follow certain rankings.
Chapter 5 deals with the theory and empirics of the spectral analysis of price of production models, as Mariolis and Tsoulfidis’ attempt to account for the empirical regularities in these models. The chapter starts by constructing the spectral representation of price and wage-profit curves. Based on a particular representation of equations [6] and [7] the authors concentrate their attention on the role that eigenvalues λH,i might play in explaining the empirical regularities by considering the implications for price and wage-profit curves of different eigenvalues configurations. After this theoretical set-up, the authors conduct an investigation of eigenvalues behavior from observed input coefficient matrices for different countries and years. They find that only the modulus of the firsts few eigenvalues have a considerable magnitude whereas the rest (the majority of them) cluster around zero, providing support to the hypothesis that the two and three-industry approximation to price and wage-profit curves, respectively, could be explained by the characteristics of eigenvalues.
Chapter 6 places an important constraint on the inference that one might make from the previous chapter: that at the limit (n→∞), all eigenvalues, except for the maximal or first eigenvalue, tend to zero. It evaluates the conjecture, made by Brody (1997), that as the size of the input coefficient matrix increases, the ratio of the modulus of the second to the first eigenvalue |λ2|/λ1 tends to zero. Not only can they not find evidence for this conjecture, but they also report magnitudes that suggest that the opposite happens.
Throughout the six chapters, the authors not only review several of the most important theoretical results and reproduce standard estimations and statistical exercises, but they also present original contributions to the theoretical and empirical debate on price of production models. These contributions constitute the basis for their main results.
First, the authors conclude that price and wage-profit curves behave qualitatively as price of production models composed respectively of only three and two industries, within the economically meaningful profit rate. Therefore, these strongly restricted systems or low-dimensional models can be used as “surrogates for actual single-product economies” (Mariolis and Tsoulfidis, 2016, p. 212).
Second, in an effort to identify the factors behind the empirical regularities in the shapes of the functions, Mariolis and Tsoulfidis provide a representation of price and wage-profit curves in terms of the spectrum of the input coefficient matrix. The authors identify certain constraints on the eigenvalues under which these functions would display the observed shapes, namely small or negligible subdominant eigenvalues (eigenvalues others than the maximal one). This low “effective rank” of the input coefficient matrix constrains the possible shapes of price and wage-profit curves.
The contrast between the empirical shapes of the functions and the analysis of their spectral representation set the ground for Mariolis and Tsoulfidis’ third main result: For all the countries, years and aggregation levels considered in their empirical research, the ranking plot and histogram of eigenvalues’ moduli has an exponential type of decay. As a result of this behavior, most of the eigenvalues’ moduli cluster around zero and only a few of them have a considerable magnitude. This empirical regularity provides support to the hypothesis that a reduced rank in the input coefficient matrix could explain the shapes in observed price and wage-profit curves.
Finally, further analysis of eigenvalues’ moduli provides evidence against the so-called Brody's conjecture. Their eigenvalue calculations suggest the opposite: as the size of the matrix increases, the modulus of the second eigenvalue increases. Moreover, the moduli of the third and fourth eigenvalue seem to increase with the matrix size as well. These results indicate that the exponential-type of shape in the ranking plot of eigenvalues moduli could be the result of two forces, one affecting eigenvalues’ moduli rate of decay and another maintaining a proportion of eigenvalues with considerable magnitude.
I would like to finish this review by giving a general recapitulation and some general conclusions that can be derived from this important book. Modern Classical Economics and Reality aims to study prices of production and the profit rate using the framework of what the authors call the “core” of the classical theory of value —which includes, among other aspects, exogenously given techniques of production (l,A), the output proportions (x), and the wage rate (ω)—. Under the assumptions given by the “core,” it is expected that prices of production constitute the center of gravity around which market prices gravitate. However, the algebraic structure of the model allows for a wide range of price and wage-profit curves which are very different in nature. Theoretically, it is possible to have considerable nonlinear behavior in the wage-profit relation, prices of production and the value of aggregate commodities (e.g. capital or capital-output ratios) as income distribution changes. In addition, it is possible for prices of production not to follow a simple rule derived from the quantity of total labor time expended in their production. Relying on a lack of a priori information on the structure of the “core” (l, A, x), the authors remain open, noncommittal about the logical possibilities of the model. Under these terms, one would expect that among the set of all the admissible results, those supporting the “traditional theories” would be very unlikely to be observed.
This is the benchmark adopted by the authors and under which they write the theoretical setting of the first chapters of the book. However, as soon as the empirical results are reported, be it by referring to the empirical literature or by presenting their own calculations, the overwhelming majority of the results suggest that the propositions implied by the “traditional theories” are actually the regular outcomes. The authors conclude that price and wage-profit curves, “more often than not,” have the behavior associated with the propositions of traditional theories. The existence of this empirical paradox to the theoretical paradoxes posed on “traditional theories” leads me to the following remarks on the book.
The authors show an interest in identifying all the relevant mathematical properties associated with the linear production models used to study prices of production and the profit rate. They also have an interest in contrasting these properties with the properties derived from “traditional theories”. However, the contrast between the economic hypotheses (or propositions) and the empirical evidence and its use to infer the economic forces that might be operating in modern capitalist economies plays a secondary role. In addition, the conclusions at which the authors arrive from this contrast (between empirical evidence and economic hypotheses) leave a somehow ambiguous feeling about its implications. Regarding the discussion of the hypotheses from traditional and non-traditional theories, it is not clear what the implications of the results are for both propositions based on the statements from the authors. For instance, does the monotonicity of the estimated price-profit curves support the propositions from neoclassical or modern classical theory? On the one hand, the authors state that price monotonicity is an important condition for neoclassical propositions4 and, at the same time, that modern classical propositions imply that this price behavior is not guaranteed.5 On the other hand, the book finds a regular empirical monotonic behavior in price-profit curves and concludes that neoclassical propositions might not hold and that “Sraffian analysis” is relevant.6
In their search for an explanation of the observed regularities generated by estimated price of production models, Mariolis and Tsoulfidis find in the behavior of eigenvalues a promising new perspective. The derived spectral representation of the model shows that under strong constraints on eigenvalues’ behavior, the theoretical models could mimic the empirical patterns. These constraints could be summarized as few eigenvalues with considerable magnitude and the rest clustered around zero. On top of that, the authors find overwhelming evidence for this type of behavior for several countries, years and aggregation levels, giving support to their hypothesis. The union of their theoretical analysis and their empirical findings represents a successful first step towards an explanation of the empirical regularities in price of production estimations. However, in order to solve the puzzle in terms posed by Mariolis and Tsoulfidis, we now need to explain why eigenvalues have this behavior. The literature7 has recently made substantial contributions to solving the puzzle but now the field has moved from the explanation of regularities in price and wage-profit curves to the explanation of regularities in the distribution of eigenvalues. We still need to explain why, if there is no a priori constraint in the “core” about the behavior of these curves and eigenvalues, we have these remarkable empirical regularities. What are the economic forces behind the observed shapes of the functions and the distribution of eigenvalues, given the different admissible possibilities from the algebra of the price of production models? The identification of these economic forces should constitute important information to be added to the “core” of the modern classical theory of value in order to explain observed capitalist economies.











 nueva página del texto (beta)
nueva página del texto (beta)