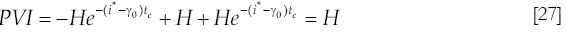Servicios Personalizados
Revista
Articulo
Indicadores
-
 Citado por SciELO
Citado por SciELO -
 Accesos
Accesos
Links relacionados
-
 Similares en
SciELO
Similares en
SciELO
Compartir
Investigación económica
versión impresa ISSN 0185-1667
Inv. Econ vol.71 no.281 Ciudad de México jul./sep. 2012
Foreign Debt, Export Dynamics and the Thirlwall's Law
Deuda externa, dinámica de las exportaciones y la ley de Thirlwall
Alejandro Rodríguez-Arana*
* Universidad Iberoamericana, Plantel Ciudad de México, <alejandro.rodriguez@uia.mx>.
Received April 2011
Accepted August 2012
Abstract
Independently of capital movements, the so called Thirlwalls's Law (Thirlwall, 1979) is theoretically a robust result in the long run. When the rate of growth of exports is equal or greater than the rate of growth of foreign debt, there is a convergence of the domestic rate of growth of Gross Domestic Product (GDP) to the original and simplest Thirlwall's rate of growth. When, furthermore, the rate of growth of foreign debt is equal or lower than the Thirlwall's rate of growth, the economy is solvent and the rate of growth of GDP converges to the Thirlwall's law.
Key words: Thirlwall's law, growth of exports.
JEL Classification:* F32, F41, F43
Resumen
Independientemente de los movimientos de capital, la llamada Ley de Thirlwall (Thirlwall, 1979) es un resultado teóricamente robusto en el largo plazo. Cuando la tasa de crecimiento de las exportaciones es igual o mayor que la tasa de crecimiento de la deuda externa, la tasa de crecimiento del producto interno bruto () converge a la tasa de crecimiento propuesta originalmente por Thirlwall. Cuando, además, la tasa de crecimiento de la deuda externa es igual o menor que la tasa de crecimiento propuesta por Thirlwall, la economía interna es solvente y, al mismo tiempo, cumple con la ley de Thirlwall en el largo plazo.
Palabras clave: ley de Thirlwall, crecimiento de las exportaciones.
INTRODUCTION
Foreign debt in developing economies has been a hot topic for many years. In the past there had been several episodes where high debt is associated with a poor performance of growth in the affected economies. Usually debt can be compared with a pair of scissors. The process of indebtedness represents fresh resources. Afterwards, the payment of interest implies a burden and the economy suffers. The dynamics of debt alters the dynamics of output and growth. The question is in what way.
It is possible to analyze the relation between output, growth and debt using different methodologies. In this paper we use the balance of payments constrained growth hypothesis (BOPCGH), an old approach originally developed by Harrod (1933), Myrdal (1957), Kaldor (1970), Prebisch (1959) and Seers (1962) and later refined by Thirlwall (1979), Thirlwall and Hussain (1982), McCombie and Thirlwall (1997), Moreno Brid (1998, 2003), McCombie (2011), among others.
The reason to use the BOPCGH and not a neoclassical model is first that BOPCGH establishes a direct link between the domestic output and the foreign output, something that in small economies is empirically relevant. Second, the BOPCGH assumes stable functions for exports and imports and in different empirical works such stability has also been proved (see for example Santos Paulino and Thirlwall, 2004). At the same time, in spite of severe criticisms that BOPCGH has received,1 different empirical papers have not been able to reject the direct relation that the approach establishes between output growth and the ratio of income elasticities of exports to imports multiplied by foreign output, another point in its favor.2 In recent times there is a considerable amount of work inspired in BOPCGH.3
The nature of debt has changed through the years. In the old days foreign debt was mainly public and was hired directly from the government of the domestic economy to government agencies of other countries, private banks or directly through international organizations. Nowadays things have changed. Though an important part of foreign debt is still public, market mechanisms have substituted direct negotiations. Nonetheless, the effects that both kinds of debt have in the economy remain similar.
The main objective of this theoretical paper is to analyze the dynamics of the balance of payments and growth in a small economy when there are debt flows that generate future interest payments on the total debt outstanding. We start from the balance of payments identity and then we model exports, imports and debt dynamics. To simplify the exercise we assume that all relative prices are constant.
Using the described methodology, we analyze the dynamics of the ratio of imports to exports. When the rate of growth of exports is equal or greater than the rate of growth of foreign debt, the rate of growth of Gross Domestic Product (GDP) of the small open economy converges to the so called Thirlwall's Law (Thirlwall, 1979), a situation where the growth of the small domestic economy is equal to the ratio of income elasticities of exports and imports multiplied by the rate of growth of GDP of the relevant foreign economy. If the rate of growth of exports is lower than the rate of growth of foreign debt, the domestic rate of growth diverges from the Thirlwall's law. However, that situation cannot last for a long time because in that case the solvency of the economy is threatened. The Thirlwall's proposition appears as a very robust result in the long run.
Thirlwall and Hussain (1982) and Moreno Brid (1998, 2003) address the validity of the original Thirlwall's law when debt and indebtedness are present. These authors conclude that in this case the Thirlwall's result changes. Perhaps the main contribution of this paper is to show that even in the presence of debt and indebtedness the original simplest Thirlwall's law can be rescued as a long run result.
This paper is divided into four sections: First this introduction; second section sets the general equations to determine —at each instant in time—the ratio of imports to exports, the value of domestic income and the domestic growth of the economy. Third section analyzes the conditions that a small economy has to show for being solvent in the long run. When these conditions hold, the original Thirlwall's law also holds in the long run; section four concludes.
THE DEBT TRAJECTORY, THE GROWTH OF EXPORTS AND THE THIRLWALL'S LAW
In this section we take the approach stated by BOPCGH: the balance of payments constraint of the economy determines domestic growth. For the mathematical analysis of the paper we use a methodology developed by ourselves.
The model used assumes a small domestic economy, which can influence neither foreign income nor the foreign interest rate. The definition of the current account is:

Where: X are total exports; m, total imports; i*, the foreign rate of interest, assumed constant; D, the total net foreign debt outstanding, and CA, the current account. All relative prices are given and normalized in one. This is certainly a strong assumption. Many relative prices do not show a trend in the long run but vary in the short run. Different authors like Thirlwall (1979), Thirlwall and Hussain (1982), Moreno Brid (1998, 2003) and McCombie (2011), among others, assume also constant relative prices at some point in their papers.
The definition of the balance of payments shows that the sum of the current account plus the capital account net of changes in international reserves must be zero. Therefore:
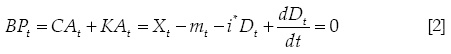
Where: KA is the capital account, dD/dt is the change in net foreign debt, which is the negative of the current account.
From equation [2] the ratio of imports to exports is defined as:
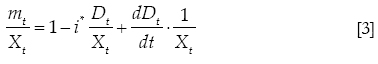
Alternatively, there will be a convergence where imports grow at the rate of exports when:

That will happen when the cumulative growth of both the interest payments of the total stock of net debt and indebtedness are lower than the rate of growth of exports.
As in Thirlwall (1979) and other works in the topic, we assume that exports and imports are given by

Where X1 and m1 are constants; γ* is foreign output, γ is domestic output; α is the elasticity of exports to foreign income and β is the elasticity of imports to domestic income.
Also, we propose a trajectory for the net foreign debt outstanding:

Therefore

Where: γ is the rate of growth of net foreign debt. We will assume that net debt is always positive (H > 0).
Exports are governed by foreign output, which instead follows the trajectory:

Where gγ* is the rate of growth of foreign GDP. Then, the trajectory of exports is given by:

The rate of growth of exports is αgγ* that is to say the elasticity of exports to foreign output multiplied by the rate of growth of foreign GDP.
Substituting equations [5] to [10] in [3] and rearranging gives as a result the ratio of imports to exports:
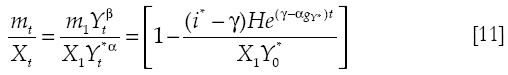
Imports will be lower than exports when the net burden of foreign debt is positive. That happens when the interest payments of the debt are higher than the renewal of such debt (i* > ϒ). In such case, there will be a net transfer from the domestic country to foreign countries. On the contrary, if i*<ϒ, there is a net transfer from foreign economies to the domestic one and imports will be higher than exports.
Differentiating equation [11] and rearranging in a tedious way (see appendix) we get the trajectory of domestic growth
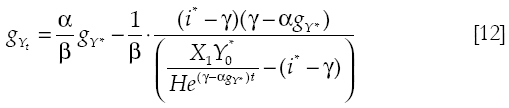
Where gγ is the growth of the domestic GDP and gγ* is the growth of foreign GDP. The term (α/β)gγ* is the Thirlwall's rate of growth, which is defined as the ratio of the elasticities of exports to imports multiplied by the rate of growth of the relevant foreign economy.
For the economy to exist, equation [11] has to be positive, which implies:
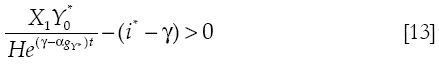
At the same time the derivative of growth with respect to time in [12] is:
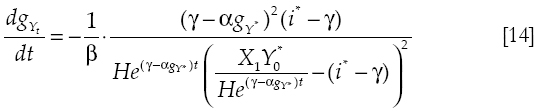
Equation [11], which defines the trajectory of the ratio of imports to exports, is also useful to determine the trajectory of income γ. Equation [12] shows the trajectory of growth, while equation [14] shows how growth evolves in time.
Based in equation [12] we make a proposition.
Proposition 1: independently of how the foreign rate of interest (i*) is with respect to the rate of growth of net foreign debt (γ), the rate of growth of the domestic economy (gγ) will converge to the Thirlwall's rate of growth ((α/β)gγ*) when the rate of growth of exports (αgγ*) is equal or greater than the rate of growth of net foreign debt (γ).
Proof: if the rate of growth of exports is equal to the rate of growth of foreign debt, the second term of equation [12] is zero and the rate of growth of domestic income is always equal to the Thirlwall's rate of growth.
If the rate of growth of exports is greater than the rate of growth of foreign debt, then in the limit, when t tends to infinity:
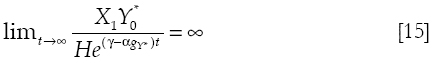
Then the denominator of the second term of equation [12] is extremely large, which in turn implies that the second term of such equation tends to zero. Therefore:

The growth of the small economy tends to the original simplest Thirlwall's rate of growth.
In the normal case, where both the foreign rate of interest and the rate of growth of exports are greater than the rate of growth of net foreign debt, actual growth of GDP (gγt) is higher than the Thirlwall's rate of growth ((α/β)gγ*) (see equation [12], i* > γ and αgγ* > γ) but converging to it (see equation [14], growth is falling in time). At the same time, the ratio of imports to exports is lower than one (see equation [11]) because the burden of the debt is positive (i* > γ). Since that burden with respect to exports is falling (αgγ* > γ), imports grow more than exports and that is the intuitive reason why GDP is above the Thirlwall's rate of growth in the short and medium terms.
Another proposition emerges when the rate of growth of debt is higher than the rate of growth of exports.
Proposition 2: independently of how the foreign rate of interest (i*) is with respect to the rate of growth of net foreign debt, when the rate of growth of such variable (ϒ) is greater than the rate of growth of exports (agY*), mathematically the rate of growth of the economy converges to the ratio γ/β which is higher than the Thirlwall's rate of growth.
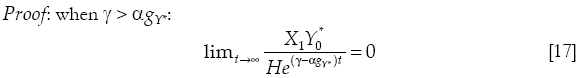
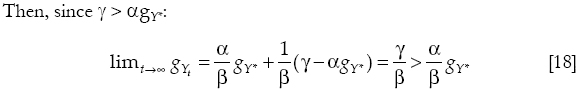
Equation [18] is just a mathematical and not an economic result. We will see in the next section that the rate of growth of net debt (γ) cannot be greater than the rate of growth of exports in the long run.4
In the short term the rate of growth of GDP may be diverging from the Thirlwall's law. For instance, suppose that the growth of debt is higher than both the foreign rate of interest and the rate of growth of exports (i* < γ; agY* < γ). If that is the case, equation [11] shows that the ratio of imports to exports is greater than one (see equation [11]). The domestic economy is receiving a net transfer from abroad. For the same reason growth is diverging from the Thirlwall's rate upwards (see equation [13]). That situation cannot last for long. The domestic economy, as we will see in the next section, is not solvent in that case.
CONDITIONS FOR THE SOLVENCY OF THE DOMESTIC ECONOMY
Propositions 1 and 2 show that the domestic growth of the economy may or may not converge to the Thirlwall's rate of growth. We will show that for the domestic economy being solvent, the conditions that must prevail in the long run imply the convergence of the domestic rate of growth to the Thirlwall's rate.
There will be solvency if the long run ratio of net foreign debt to domestic income converges either to zero or to a constant value. It would be possible to establish an upper limit for that constant.
We make another proposition.
Proposition 3: when the rate of growth of debt is lower or equal than both the rate of growth of exports and the Thirlwall's rate of growth, the ratio of foreign debt to domestic income converges to zero or to a constant, but then proposition 1 implies that the domestic rate of growth converges to the Thirlwall's rate of growth.
Proof: domestic income may be obtained substituting equation [9] on equation [11]:
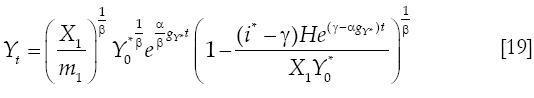
Foreign debt is defined by equation [7]. Then the ratio of foreign debt to domestic income is defined as:
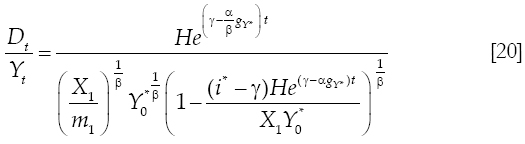
This ratio will be zero or constant in the long run if:
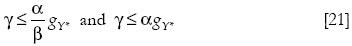
Because in that case:

But if that happens, then proposition 1 implies that the domestic rate of growth converges to the Thirlwall's law.
Conditions in equation [21] are sufficient for solvency. We will show now that they are also necessary.
In the long run, the foreign rate of interest must be higher than the rate of growth of net debt; otherwise lenders would have infinite capital losses.
For lenders to be satisfied, the present value of the interest payments of net debt must be higher or equal than the actual value of debt. That is to say:
PVI ≥ H [23]
Where PVI is the present value of the interest payments of net debt. When the rate of interest and the rate of growth of net debt take just one value along the time path, PVI is defined as:
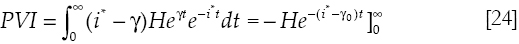
This term is equal to H, the actual value of net debt, when If i* >γ, and to minus infinity when i* < γ. Not a single lender will generate a perpetual loan growing above the foreign rate of interest. Then i* must be above γ. It is relatively easy to extend this result when the rate of growth of debt takes two values in time.5
The intuition here is clear. If i* were always lower than γ, there would be a perpetual transfer from foreign economies to the small economy and debt would not be a liability but an asset. The nature of debt implies a cost.
For the domestic economy to exist Yt > 0, but that only happens if (see equations [13] and [19]):
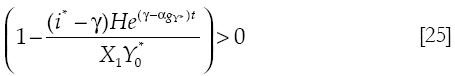
Then since i* >γ in the long run, the rate of growth of debt (γ) must be equal or lower than the rate of growth of exports (αgY*) as t grows, otherwise the domestic economy would disappear (ϒ would become negative). But if in effect αgY*> γ, for the ratio of debt to income being zero or a constant, the rate of growth of net debt must be lower than the Thirlwall's rate of growth (see equation [20]). Therefore, conditions in equation [21] are not only sufficient for the solvency of the domestic economy, they are also necessary.
If conditions for solvency hold, the rate of growth of GDP of the domestic economy converges to the Thirlwall's rate of growth.
CONCLUDING REMARKS
The BOPCGH is a useful approach to analyze different problems observed in small economies with strong links to large economies. In this paper we show that the original Thirlwall's Law is theoretically a long run robust result. This happens even in the presence of capital inflows because such result (the Thirlwall's Law) finally shows that the economy is solvent.
The analysis of capital flows in the context of the BOPCGH has been carried on by Thirlwall and Hussain (1982), McCombie and Thirlwall (1997), Moreno Brid (1998, 2003), among others. However, in the majority of cases the analysis performed by these researches is more static than dynamic, using a methodology that is good for knowing the rate of growth of the domestic economy at a certain moment of time, when the rate of growth of capital inflows takes some particular value, but that is not very useful to analyze the complete trajectory of debt, exports and the GDP itself. In this one respect we expect to improve this analysis with a more dynamic view.
In this paper we analyze the trajectory of growth, income and the ratio of net foreign debt to income when the foreign rate of interest and the rate of growth of debt take just one value along the time path. In that case the solvency of the economy requires the rate of growth of debt being lower than three variables: the rate of growth of exports, the Thirlwall's rate of growth and the foreign rate of interest. When that happens, the rate of growth of income of the domestic economy converges to the Thirlwall's rate of growth.
In real life we observe that sometimes the rate of growth of debt is higher than the three described variables in the last paragraph, nonetheless.
The analysis of this paper can be extended- in a relatively easy way- to cases where temporarily the growth of debt is higher than one, two or the three variables already explained. In that case the condition is that from sometime in the future onwards the rate of growth of debt must fall below the rate of growth of exports, the Thirlwall's rate of growth and the foreign rate of interest.
The BOPCGH is an excellent tool to analyze certain situations where the rate of growth of foreign economies affects domestic growth. That is especially true in countries whose main partners are large economies, like the case of Mexico with respect to the U.S. The problem with BOPCGH is the lack of microeconomic fundamentals. There has been a mutual despise between neoclassical and non-neoclassical economists. That is not a way to solve problems in the profession. From the neoclassical point of view there should be a genuine interest in an approach that provides accurate predictions though its fundamentals are still weak. From the non-neoclassical perspective there should be an interest to provide the approach of microeconomic fundamentals.
REFERENCES
Alonso, J.A., 1999. Growth and the External Constraint: Lessons from the Spanish case. Applied Economics, 231(2), pp. 245-53. [ Links ]
Araujo, R. and Lima, G., 2007. A Structural Economic Dynamics Approach to Balance of Payments Constrained Growth. Cambridge Journal of Economics, 31(5), pp. 755-74. [ Links ]
Atesoglu, H.S., 1993. Balance of Payments Constrained Growth: Evidence from the United States. Journal of Postkeynesian Economics, 15(4), pp. 507-14. [ Links ]
Cline, W, 1982. Can the East Asian Model of Development be Generalized? World Development, 10(2), pp. 81-90. [ Links ]
Felipe, J., 2009. Inclusive Growth, Full Employment and Structural Change Implications and Policies for Developing Asia. London, England: Anthem Press. [ Links ]
Gouvea, R. and Lima, G., 2010. Structural Change, Balance of Payments Constraint and Economic Growth: Evidence from the multisectoral Thirlwall's law. Journal of Post Keynesian Economics, 33(1), pp. 169-204. [ Links ]
Harrod, R., 1933. International Economics. Cambridge, England: Cambridge University Press, 207 p. [ Links ]
Houthakker, H. and Magge, P., 1969. Incomes and Price Elasticities in World Trade. Review of Economic and Statistics, 51(2), pp. 111-25. [ Links ]
Holland, M., Vieira, F. and Canuto, O., 2004. Economic Growth and the Balance of Payments Constraint in Latin America. Investigación Económica, 63(247), pp. 45-74. [ Links ]
Kaldor, N., 1970. The Case for Regional Policies. Scotish Journal of Political Economy, 17(3), pp. 337-48. [ Links ]
Krugman, P., 1989. Differences in Income Elasticities and Trends in Real Exchange Rates. European Economic Review, 33(5), pp. 1031-54. [ Links ]
López, J. and Cruz, A., 2000. Thirlwall's Law and Beyond: The Latin American experience. Journal of Postkeynesian Economics, 22(3), pp. 477-95. [ Links ]
McCombie, J., 2011. Criticisms and Defenses of the Balance of Payments Constrained Growth Model: Some old, some new. PSL Quarterly Review, 64(259), pp. 353-92. [ Links ]
McCombie, J. and Thirlwall, A.P., 1979. The Dynamic Harrod Foreign Trade Multiplier and the Demand Oriented Approach to Economic Growth: An evaluation. International Journal of Applied Economics, 11(1), pp. 5-26. [ Links ]
McGregor, P. and Swales, J., 1985. Professor Thirlwall and Balance of Payments Constrained Growth. Applied Economics, 17(1), pp. 1265-74. [ Links ]
Moreno Brid, J.C., 1998. On Capital Flows and the Balance of Payments Constrained Growth Model. Journal of Postkeynesian Economics, 21(2), pp. 283-97. [ Links ]
Moreno Brid, J.C., 2003. Capital Flows, Interest Payments and the Balance of Payments Constrained Growth Model. Metroeconomica, 54(2-3), pp. 346-65. [ Links ]
Myrdal, G., 1957. Economic Theory and Underdeveloped Regions. London, England: Duckworth, 182 p. [ Links ]
Palley, T., 2002. Pitfalls in the Theory of Growth: An application to the balance of payments growth model. In: Setterfield, M. ed. The Economics of Demand Led Growth. Cheltenham: Edward Elgar Publishing Limited. [ Links ]
Palley, T., 2003. Export Led Growth: Evidence of developing country crowding out. In: Arestis, P., Baddeley, M. and McCombie, J. eds. Economic Integration, Regionalism and Globalisation. Cheltenham: Edward Elgar Publishing Limited. [ Links ]
Prebisch, R., 1959. Commercial Policies in the Underdeveloping Countries. American Economic Review, 49(2), Papers and Proceedings, pp. 251-73. [ Links ]
Santos Paulino, A. and Thirlwall, A.P., 2004. The Impact of Trade Liberalisation on Exports, Imports and the Balance of Payments of Developing Countries. Economic Journal, 114(493), pp. F50-72. [ Links ]
Seers, D., 1962. A Model of Comparative Rates of Growth of the World Economy. Economic Journal, 72(285), pp. 45-78. [ Links ]
Setterfield, M., 2006. Thirlwall's Law and Palley's Pitfalls: A reconsideration. In: Growth and Economic Development: Essays in honor of A..P. Thirlwall. Cheltenham: Edward Elgar Publishing Limited. [ Links ]
Thirlwall, A.P., 1979. The Balance of Payments Constraint as an Explanation of International Growth Rate Differences. Banca Nazionale de Lavoro Quartely Review, 128(32), pp. 45-53. [ Links ]
Thirlwall, A.P., 1991. Professor Krugman's 45-Degree Rule. Journal of Postkeynesian Economics, 14(1), pp. 23-8. [ Links ]
Thirlwall, A.P. and Hussain, M. The Balance of Payments Constraint, Capital Flows and Growth Rate Differences Between Developing Countries. Oxford Economic Papers, 34(3), pp. 498-510. [ Links ]
* JEL: Journal of Economic Literature-Econlit.
I would like to thank two anonymous referees for very helpful comments.
1 BOPCGH has been criticized in numerous times: Some of the main critiques are the following: First that there is not necessarily a casual relation between the growth of exports and the growth of income and that the equilibrium of the balance of payments is independent of the domestic growth (McGregor and Swales, 1985). Second, that the relation between the growth of domestic income and the ratio of the elasticities of exports to imports, multiplied by the rate of growth of foreign income, goes from the former to the latter and not the other way around (Krugman, 1989), Palley, 2002). Third, that the export led growth that emerges from the bopch analysis may be criticized on the grounds of the fallacy of composition, because not all countries could grow applying that suggestion (Cline, 1982; Palley, 2003). McCombie (2011) explains these critiques and the answer to them from the bopch approach. Thirlwall (1991) criticizes Krugman (1989). Setterfield (2006) also defends the bopch especially against Pallets critiques (Palley, 2002, 2003).
2 See for example, Alonso (1999); Atesoglu (1993); Holland, Vieira and Canuto (2004); López and Cruz (2000); McCombie and Thirlwall (1997), among others. A quite old paper in this respect is the one of Houthakker and Magee (1969).
3 See for example, Araujo and Lima (2007); Felipe (2009); Gouvea and Lima (2010), and McCombie (2011), among others.
4 When, i* >γ> αgγ*, growth is below the Thirlwall's rate (equation [12]) and falling (equation [14]). In this case the economy collapses at some point (see equation [11]), this happens whenthe term 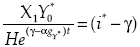 in equation [12]. The time when that happens is:
in equation [12]. The time when that happens is:
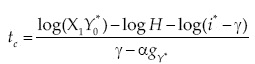
This time will be positive if the term X1Y0* is sufficiently high. Mathematically, once the economy collapses, growth goes to minus infinity and then jumps to a positive value greater than ϒ/β and continues falling until at the end is γ/β.
5 Suppose that the growth of debt takes two values along the time: γ0 > i* in the interval (0,tc) and γ1< i* in the long run interval (tc ∞). The PVI in this case is:
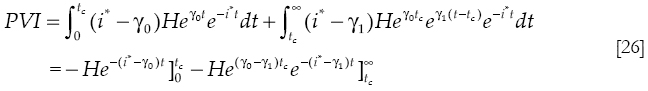
Which in turn becomes: