Servicios Personalizados
Revista
Articulo
Indicadores
-
 Citado por SciELO
Citado por SciELO -
 Accesos
Accesos
Links relacionados
-
 Similares en
SciELO
Similares en
SciELO
Compartir
Investigación económica
versión impresa ISSN 0185-1667
Inv. Econ vol.69 no.274 Ciudad de México oct./dic. 2010
Dimensional analysis of price–value correspondence: a spurious case of spurious correlation
Análisis dimensional de la correspondencia valor–precio: un caso espurio de correlación espuria
Alejandro Valle Baeza*
Facultad de Economía de la Universidad Nacional Autónoma de México (UNAM). E–mail: valle@servidor.unam.mx.
Manuscrito recibido en mayo de 2010.
Aceptado en septiembre de 2010.
Abstract
In labor theory of value there are empirical studies showing strong association between labor values and market prices. Some critics (Kliman 2002; Diaz and Osuna 2007, 2009) have questioned such empirical findings because: a) there is a problem of spurious correlation involved, and b) measures of association vary with changes in the physical units of the analyzed merchandises.
We shall see that there is a difficulty stemming from the definition of the problem as well as the question of the dimension of the mathematical models used. Our main conclusions state that critics are wrong, and empirical studies are solid enough. These conclusions will be supported by two reasons: a) the existence of a spurious correlation does not apply to this problem according to the dimensional analysis; and b) dimensional analysis is essential to adequately pose the problem of price–value association and thus to obtain measures that do not change with variations of units of measurement.
Keywords: value theory, dimensional analysis, spurious correlation.
JEL Classification:** C52, D46, D57, E11
Resumen
Existen estudios empíricos que muestran una fuerte asociación entre los valores trabajo y los precios de mercado. Algunos (Kliman 2002; Diaz and Osuna 2007, 2009) han criticado tales resultados empíricos porque: a) existe un problema de correlación espuria, y b) las medidas de asociación varían ante cambios en las unidades físicas de las mercancías analizadas.
Se verá que existe una dificultad derivada de la definición del problema así como de la cuestión de la dimensión de los modelos matemáticos utilizados. Nuestras principales conclusiones son que tales críticas son incorrectas y que los estudios empíricos son suficientemente sólidos. Tales conclusiones se encuentran respaldadas por dos razones: a) la existencia de una correlación espuria no se aplica a este problema de acuerdo con el análisis dimensional y b) el análisis dimensional es esencial para plantear adecuadamente el problema de la asociación valores–precios y, por tanto, obtener medidas que no se alteren con cambios en las unidades de medición.
Palabras clave: teoría del valor, análisis dimensional, correlación espuria.
INTRODUCTION
Labor theory of value has received considerable attention among Marxists and their critics. No agreement has been reached as to what labor theory of value is (Foley, 2000), Itoh, 1988; Kliman, 2006; Laibman, 1992 and Mohun, 2000). Paradoxically there are empirical studies showing strong association between labor values and market prices. Such works could inject new energy into Marxist theory of value; nevertheless some critics have questioned such empirical findings because: a) there is a problem of spurious correlation involved, and b) measures of association vary with changes in the physical units of the analyzed merchandises.
We shall see that in this discussion there is a difficulty stemming from the definition of the problem as well as the question of the dimension of the mathematical models used. Our main conclusions state that critics are wrong, and empirical studies are solid enough. These conclusions will be supported by two reasons: a) the existence of a spurious correlation does not apply to this problem according to the dimensional analysis, so well known in natural sciences, but seldom applied in economical problems; and b) dimensional analysis is essential to adequately pose the price–value association problem and thus to obtain measures that do not change with modifications of units of measurement.
In the first part of this paper we describe the problem of measuring value–price correspondence as it has been described in literature. In the second part we focus on what we consider the main aspects of dimensional analysis in order to correctly pose the problem in the third part of this paper. Some brief conclusions on the matter are presented in the final section.
POSING THE PROBLEM
An important aspect of discussions about the validity of Marxist value theory comes from a paper by Anwar Shaikh (1984), who found for the United States of America (USA) and Italy a close correspondence (measured through the correlation coefficient) between labor values and market prices. Shaikh reinterpreted data published by Leontief (1986) as an estimate of labor values according to the method developed by Morishima and Seton (1961), and he concluded that there was a strong correspondence between prices and labor values.1 Shaikh compared gross production in USA in terms of market prices pi xi, with gross production in terms of labor value λixi.Because available data were aggregated due to practical needs, Shaikh did not attain λi values. Likewise, he worked with data from Marzi and Varri (1977) for Italy, and attained similar conclusions.
Ochoa2 (1984) in his Ph. D. dissertation used all the data available and confirmed Shaikh's findings for the usa. In that same publication Ochoa points out that correlation coefficient between different kinds of prices and equivalence prices (also called direct prices by Shaikh) is the object of over valuation due to problems of spurious correlation;, also it can change with measure units. He emphasized that if measure units are adequately manipulated, correlation coefficient between values and prices can be increased or decreased. Petrovich (1987) mentioned, without highlighting it, the problem of spurious correlation and introduced root mean square deviation as an alternative to correlation coefficient. With the aim to reduce the problem of spurious correlation, Ochoa (1984, 1989) introduced absolute mean deviation and absolute weighted mean deviation as a way to measure value–price correspondence. Other works have confirmed the findings for the USA with other countries.3 Kliman (2002) explained that strong correlations between values and prices came from spurious correlation and that when data were fixed through an industry size index there was no strong correlation between values and prices. Cockshott and Cottrell (2005) refuted Kliman and asserted that criticism of spurious correlation did not apply. Díaz and Osuna (2009, 2007 and 2006) criticized both sides of the discussion arguing that the problem was one of indeterminacy: "The key problem is one of indeterminacy in the relation among prices and labor values, which derives from the necessary arbitrariness in the selection of the physical units of measurement for commodities", as Ochoa (1984) first noticed.
This problem of indeterminacy is a theoretical problem, and not a "technical" or computing problem. An important consequence of such a problem is that it invalidates the entire analysis of cross–sectional correlation between prices and labor values, as our empirical exercise for the case of Spain shows.
The conclusion is that nothing can be said on empirical cross–sectional correlation among different classes of prices. Hence, in Ludwig Wittgenstein's own words: whereof one cannot speak, thereof one must be silent (Díaz and Osuna 2006:262).
We shall see that the critics telling us to remain silent are out of proportion with the strength of their refutations; but first it is essential to bring in some elements missing in the discussion: dimensional analysis.
BRIEF DESCRIPTION OF DIMENSIONAL ANALYSIS
Brody (1974) puts forward three main purposes of the dimensional analysis of an economic problem, of the correct and explicit use of measure units.
First, it is impossible to quantify scientific categories without a non ambiguous definition of our basic measure units.
Second, dimensional analysis provides verification for the logic of equations.
Third, the most important result of dimensional analysis is that it helps us express economical laws so that they are not affected by changes in measure units.
Okishio (1982) sums up the basic aspects of dimensional analysis. Here we only include three essential equations.
Assuming x[m] and y[m] the x and y magnitudes with measure units m, for example 3 is the y magnitude and $/Kg are the units. We have three basic rules.
Addition or subtraction of magnitudes with same units are allowed:

Addition or subtraction of magnitudes with different units are not allowed:
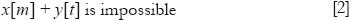
Multiplication and division of magnitudes with different units are valid

A price has magnitude pi with $/ui units and labor value has a magnitude λi with units d/ui units, where d stands for labor time, $ is a monetary unit and ui is the merchandise physical unit i, a kilogram of corn, for example.
It must be emphasized what Brody states as the most important result of the dimensional analysis: it helps express the economical laws in a way that they are not affected by changes in measure units. That is to say, the problem of value–price correspondence is generally wrongly posed and when it is correctly stated it seems to have been inadvertently so.
DIMENSIONALLY CORRECT EXPRESSION OF THE PROBLEM OF VALUE–PRICE CORRESPONDENCE
Ochoa (1984) supports the idea that value theory has a strong empirical hold; nevertheless he was the first one to state a problem of spurious correlation and asserted that it is possible to increase the correlation coefficient through the modification of the measure units in the data. Thus he himself opened a way apparently leading to the invalidation not only of his own empirical work but also of every work of this kind made so far and in the future. Notwithstanding, there is a problem that should be obvious: spurious correlation exists when correspondence between two variables needs to be studied. In such a case, two observation series pi and λi, and the use of correlation or any other technique would be a way to measure correspondence between both variables. But if we only had pixi and λi xi we would be facing a problem of spurious correlation and high correlations found in empirical works would be questioned. The use of other techniques such as absolute weighted mean deviation applied by Ochoa and others could not end the problem.
Nevertheless, in our case we are dealing with vectors, not with simple variables: the vectors of prices and values consist of different variables, prices and values of different commodities, not of different observations of two variables. Maybe because they observed this difference, Ochoa and Díaz and Osuna talk about Cross section analysis. As if the purpose were to look at the behavior of two variables in time and because there are no such data, it is assumed that vectors of those variables will represent them. For example Gross Domestic Product (GDP) per capita of different countries with different magnitudes will represent what happens to a country through time.
The kinds of assumptions used to make cross–sectional analysis are usually very risky, but in our case they are not feasible.
The problem can be posed clearly: How far are market prices from equivalence prices, which would exactly correspond to values? The answer, if we assume that money is a merchandise, is a simple one. Equivalence prices p*i would be:

Where λd is the value of money.
When fiduciary money replaces merchandise money equivalence prices are defined as:

μ is any positive constant.
Common current price is usually different from this. We can subtract both and measure the distance between them. As we just saw, a price is an ordered pair consisting of the magnitude and its corresponding units, and prices can be subtracted because they have the same units.

Where πi is a number with units [$/ui]is the monetary unit, and ui is the physical unit of merchandise i.
It is important to emphasize that λi can not be placed instead of p*i in equation [5], and that, strictly speaking, each time we mention values we are talking about equivalence prices in order to be able to compare them with other prices.
Equation [5] reveals a problem: if the value of money is modified (or if J is changed, in the case of fiduciary money), and if prices change accordingly, the difference also changes, i.e. if the value of the monetary unit changes, equation [5] can not be simply compared in time terms because it is in unit terms. A peculiar example of the lack of dimensional analysis is the concern of Steedman and Tomkins (1998) who find a measure of deviation between values and price to be immune to changes in the price standard. This "unchanging measure" in front of dimensional changes makes no sense; it is only a matter of a wrongly stated problem. If money merchandise is changed, deviations between current and equivalencial price of the same merchandise estimated for instance with equation [5], would be in different units and they simply could not be compared. As the comparison between them is invalid, Steedman's and Tomkins' concerns are of no use.
Another problem can be found when trying to study a group of merchandises. Equation 5 cannot be added for different merchandises. This simple rule of dimensional analysis is often infringed in discussions. For example in Petrovic (1987:2), Steedman and Tomkins (1998:382), Díaz and Osuna (2009:430).
The rule of adding up only magnitudes with homogeneous units is infringed when assuming the correlation between values and prices: the sum of the price of a car and the price of a kilogram of sugar makes no sense, as equation [2] states. Values can not be added up either; so averages of values and prices make no sense. It follows from this that correlation between values and prices cannot be directly estimated.
Thus, the alleged "non spurious" correlation between values and prices cannot exist: therefore there is no such spurious correlation.
The problem seems to be solved by taking percentage deviations: for example, Ochoa (1984:52) proposed the mean absolute deviation (MAD)defined as:

This equation allows us to highlight the necessary but insufficient aspect of dimensional analysis. After removing the units through division we can add up but the sum might not be correct. That is, if we infringe the rules of dimensional analysis there is something wrong, but obeying them does not free us from verifying the coherence of our actions. There is no point, for instance, in working out the average of percentages with different bases: the average percentage of literate people in China and Hong Kong can not be attained through simple averages of percentages in both regions. To work out mad, deviations are averaged in like numbers by one, with different basis, relative deviation of a jet's price is added up to a kilogram of sugar and the average is estimated on an equal footing.
To calculate MAD represents a mistake of this kind: variation of an airplane price is added to price a change of a pencil; because both are in percentage terms. This is just wrong.
Ochoa proposed weighted absolute mean deviation:
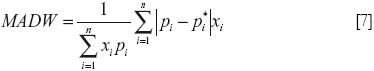
The result of multiplying a price pi[$/ui] by the xi[ui] amount is pixi[$]; the result of multiplying λi[d/ui] by the xi[ui] amount is λixi[d]. These magnitudes can now have means and variances, they can be correlated, and so on.
In short, the fact that Corr(pi,λi) cannot be defined and that Corr(pixi,λixi) does exist means that the problem of correspondence value–price can only be defined by a given X merchandise basket with xi elements. If one makes the correlation between prices and values, a basket should be considered, for example the unitary (xi = 1[ui] for each i). The "true" correlation would be the one of unitary baskets in value and in price. Nonetheless, there is no selection criterion to consider the unitary basket better than any other; on the contrary there is a better basket than the unitary, as we shall explain below.
Considering the Corr(pixi,λixi)4 correlation or the MADW, as Shaikh and Ochoa did, has some advantages over other aggregated measures of value–price correspondence, because it takes into account the relevance of merchandises both for their unitary value as well as for the volume actually produced.
Because of all this the problem of spurious correlation does not exist.
Does correlation change when measure units are modified as Ochoa stated and Díaz and Osuna stressed? No.
Ochoa's error is revealed considering that if pi and λi are directly correlated, when modifying measure units the data and the correlation are also modified. For example, if the price is in dollars per long ton of copper and is modified to put it in cents of a dollar per pound, the correlation coefficient is changed. But direct correlation between value and price, as dimensional analysis states, is wrong. We must correlate pixi with λixi and if measure units are modified for x, production, values and prices must be modified accordingly so that to keep the value of merchandise basket unaltered because monetary value of the studied element does not change. If, for instance, xk were 1 ton of steel, a valid change in units would be to put 1000 kilograms of steel, but both the price and the value should be divided by 1 000, and thus pixi and λixi will not change. This is the third application for dimensional analysis stated by Brody. The fact that results change when units are modified is a clear sign that the problem is wrongly posed. To sum up vectors pixi and λixi are unchanged in front of changes in measure units. Because of this, it is not the same to correlate pi and λi (which would be altered with changes in measure units) than to correlate pixi and λixi when xi = 1 for each i.
Correctly posing the problem with the help of the dimensional analysis does not solve the matter in the most convenient way of measuring the correspondence between values and prices. If we study the correct situation, every measures can be applied and then it can be discussed which one is better than the others. Also the correct approach allows us to see that if the basket used is changed the results can not be compared. Exactly as when inflation is measured: inflation is the variation of the monetary value of a specific basket.
CONCLUSION
In order to measure the association between labor values and prices, it is necessary to define a basket of merchandises. The correlation of market prices multiplied by gross production pixi and labor values λixi multiplied by gross production is well defined. This correlation was erroneously called 'spurious correlation' by many authors. The products pixi and λixi do not change with variations of physical units of merchandise; hence association measures cannot change accordingly.
Shaikh solved the problem of correspondence between values and prices through the correlation between pixi and λixi. For practical purposes this was correctly stated, but while failing to dimensionally verify his solution he let the door open for the errors made by Ochoa and others that followed him. Ochoa started the errors that later were enlarged, although he also attained correct results. It can be said that Ochoa's biggest mistake was, out of intellectual honesty, to question his own results. Criticism from Kliman and Steedman are useful because they help to consolidate the empirical results attained to this date. Detailed works by Díaz and Osuna are valuable to overcome the false problem of spurious correlation. The problem of temporary variation in value–price correspondence will have to be dealt with in future paper.
REFERENCES
Arda, M., An Intersectoral Study of the Turkish Economy: Variations on Price Schemes Derivable from Input–Output Tables, California, Berkley University Ph.D. Thesis, 1976. [ Links ]
Brody, A., Proportions, Prices and Planning. A mathematical restatement of the labor theory of value, Budapest, Akadémiai Kiadó, 1974. [ Links ]
Cockshott, P. and A. Cottrell, "Robust correlations between prices and labour values: a comment", Cambridge Journal of Economics, vol. 29, no. 2, 2005, pp. 309–316. [ Links ]
Cockshott P.; A. Cottrell and G. Michaelson, "Testing Marx: some new results from uk data", Capital and Class, no. 55, 1995, pp. 103–129 [ Links ]
Díaz, E. and R. Osuna, "Can we trust in cross–sectional price—value correlation measures? Some Evidence from the Case of Spain (1986–1994)", Journal of Post Keynesian Economics, vol. 28, no. 2, 2006, pp. 345–364. [ Links ]
––––––––––, "From correlation to dispersion: geometry of the price–value deviation", Empirical Economics, vol. 33, no. 3, 2007, pp. 389–399. [ Links ]
––––––––––, "Indeterminacy in price–value correlation measures", Empirical Economics, vol. 36, no. 2, 2009, pp. 427–440. [ Links ]
Foley, D., "Recent developments in the labor theory of value", Review of Radical Political Economics, vol. 32, no. 1, 2000, pp. 1–39. [ Links ]
Guerrero, D., "Insumo–producto y teoría del valor trabajo", Políticay Cultura, no. 13, 2000, pp. 139–168. [ Links ]
Itoh, M., The Basic Theory of Capitalism, New Jersey, Barnes & Noble, 1988. [ Links ]
Kliman, A., "The law of value and laws of statistics: sectoral values and prices in the u.s. economy, 1977–1997", Cambridge Journal of Economics, vol. 26, no. 3, 2002, pp. 299–311. [ Links ]
––––––––––, Reclaiming Marx's "Capital": A Refutation of the Myth of Inconsistency, Lanham, Lexington Books, 2006. [ Links ]
Kyn, O.; B. Sekerka and L. Hejl, "A model for the planning of prices", in C. Feinstein (ed.), Socialism, Capitalism and Economic Growth, Cambridge, Cambridge University Press, 1967, pp. 101–124. [ Links ]
Laibman, D., Value, Technical Change and Crisis, New York and London, M.E. Sharpe, 1992. [ Links ]
Leontief, W, Input–output economics, New York, Oxford University Press, 1986. [ Links ]
Marzi, G. and P. Varri, Variazioni di Produttività Nell'Economia Italiana: 1959-1967, Bologna, II Mulino, 1977. [ Links ]
Mohun, S., "New solution or re(in)statement? A reply", Cambridge Journal of Economics, vol. 24, no. 1, 2000, pp. 113–117. [ Links ]
Morishima, M. and F. Seton, "Aggregation in Leontief matrices and the labor theory of value". Econometrica, vol. 29, no. 2, 1961, pp. 203–220. [ Links ]
Ochoa, E., Eabour Values and Prices of Production: an Interindustry Study of the U.S. Economy, 1947—1972, New York, New School for Social Research Ph.D. Thesis, 1984. [ Links ]
––––––––––, "Values, prices, and wage–profit curves in the us economy", Cambridge Journal of Economics, vol. 13, no. 3, 1989, pp. 413–429. [ Links ]
Okishio, N., "Dimensional analysis in economics", Kobe University Economic Review, no. 28, 1982, pp. 31–44. [ Links ]
Petrovich, P., "The deviation of production prices from labor values: some methodology and empirical evidence", Cambridge Journal of Economics, vol. 11, no. 3, 1987, pp. 197–210. [ Links ]
Shaikh, A., "The transformation from Marx to Sraffa", in E. Mandel and A. Freeman (eds.), Ricardo, Marx, Sraffa, London, Verso Books, 1984, pp. 43–84. [ Links ]
Steedman, I. and J. Tomkins, "On measuring the deviation of prices from values", Cambridge Journal of Economics, vol. 22, no. 3, 1998, pp. 379–385. [ Links ]
Tsoulfidis, L. and T. Maniatis, "Values, prices of production and market prices: some more evidence from the Greek economy", Cambridge Journal of Economics, vol. 26, no. 3, 2002, pp. 359–369. [ Links ]
Valle, A., "Correspondence between labor values and prices: a new approach", Review of Radical Political Economics, vol. 26, no. 2, 1994, pp. 57–66. [ Links ]
* I am indebted with two anonymous referees, with Enrique Hueda, who enlighten a central point of this paper, and with Cesar Sánchez for useful comments. As usual all, remaining errors are my own responsibility.
** JEL: Journal of Economic Literature–Econlit.
1 There were estimates of labor values for other countries before the estimates made by Shaikh (1984) for the USA,. See for instance Kyn et al. (1967) and Arda (1976).
2 "It is clear that we can increase or decrease the extent of common variation of P (prices) and M (values) by judicious manipulation of the physical units. In fact, by appropriately rescaling the physical units used, we can make R2 vary from 0 to (asymptotically) 1" (Ochoa 1984:130).
3 For instance, see Cockshott and Cottrell (1995) for the United Kingdom, Valle (1994) with an alternative approach to estimate gross production in value, Guerrero (2000) for Spain and Teosulfides y Maniatis (2002) for Greece.
4 To obtain such correlation coefficient it is necessary to assume a linear regression model xi pi= α + βλixi with α and β with proper unities of measure.














