1. Introduction
Runaway O stars pass through the Galactic disk at velocities of ≈ 100 km s−1 (see, e.g., Cruz-González et al. 1974). These stars interact with the interstellar medium of the disk, forming an inner stellar wind bow shock, and an outer “cometary” HII region. Observations of these structures are presented, e.g., by Van Buren et al. (1995) and Noriega-Crespo et al. (1997). We note that these HII regions have a somewhat elongated “tear-drop” shape, and that the “cometary” label that is applied to them is somewhat misleading.
The problem of the cometary HII region for a star in hypersonic motion was solved analytically by Rasiwala (1969) and numerically by Thuan (1975). Axisymmetric gasdynamic simulations of this flow were presented by Raga et al. (1997).
The standard, ram-pressure balance stellar wind bow shock has the well used analytic solution of Dyson (1975). Also, at a somewhat surprisingly later time, an analytic solution to the full, thin shell stellar wind bow shock problem (including the “centrifugal pressure”) was found (Wilkin 1996; Cantó et al. 1996). The stellar wind bow shock problem has been studied extensively with gasdynamic numerical simulations (see, e.g., Stevens et al. 1992).
Stellar wind bow shock models have been used to model compact/ultracompact HII regions formed by young O stars within molecular clouds (e.g., Van Buren 1990; Mac Low 1991), moving at velocities of a few km/s through the surrounding cloud. The models for these objects generally assume that the ionization front is trapped within the stellar wind bow shock, so that the flow differs from the detached bow shock/HII region found in runaway O stars. Gasdynamic simulations of bow shock compact HII regions have been presented by Arthur & Hoare (2006).
Simulations of bow shocks around runaway stars have been computed including thermal conduction (Meyer et al. 2014) and magnetic fields (Meyer et al. 2017). The cometary HII regions surrounding these bow shocks have been modeled in detail (in axisymmetry and 3D, including an environmental magnetic field) by Mackey et al. (2013). Interestingly, even in the work of Raga et al. (1997), which modeled both the bow shock and the cometary HII region of runaway O stars, these two structures of the flow have been considered separately. In the present paper we explore the regime in which the bow shock, while not trapping the ionization front, produces a substantial absorption of the stellar ionizing photons, therefore modifying the surrounding HII region.
We describe the flow by considering the thin shell analytic solution (of Wilkin 1996; Cantó et al. 1996 and Cantó et al. 2005) for the stellar wind bow shock. A review of this solution is presented in § 2. We then write a modified form for the equation of Rasiwala (1969) and Raga et al. (1997), including the absorption of ionizing photons by the bow shock (§ 3) and integrate it numerically to obtain the selfconsistent HII region+bow shock solution for a set of parameters (§ 4). Finally, in the summary (§ 5) we diScuss the possible application of the new model for the case of compact/ultracompact HII regions, and the further steps that will be necessary to study the full parameter space of these objects.
2. The Bow Shock
A star with an isotropic wind of mass loss rate ṀW and (terminal) wind velocity vw moving hypersonically at a velocity va through a uniform medium of density ρa produces a double bow shock (with one shock stopping the wind and the second shock pushing the environment). This is shown schematically in Figure 1, as seen in a reference system moving with the star.
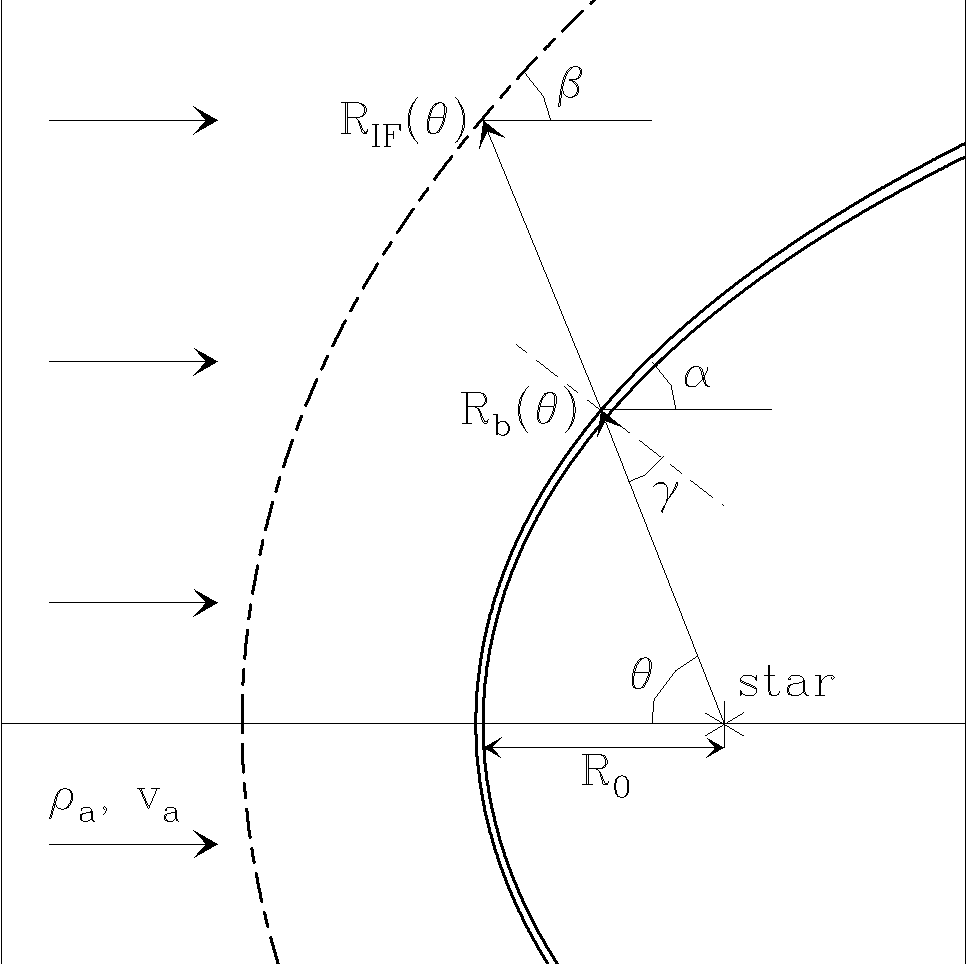
Fig. 1 Schematic diagram showing a star with an isotropic wind interacting with a uniform, streaming environment (of density ρa and velocity va). A two-shock stellar wind bow shock with a locus Rb (θ) (two thick, solid curves) and a detached ionization front of locus RIF (θ) (thick, dashed curve) are formed. The angles θ, α and γ (used in the derivation of the model equations) are shown.
Wilkin (1996) and Cantó et al. (1996) found an analytic solution for the steady, thin shell stellar bow shock problem:
with
with and where the polar angle θ and the spherical radius are shown in Figure 1.
Interestingly, the axisymmetric gasdynamic simulations of Raga et al. (1997) show that even though the bow shock driven by a runaway O star has a complex, time-dependent structure and a separation of ≈ 0.3R0 between the two bow shocks, it still approximately follows the thin shell solution of equation (1). We therefore adopt this thin shell solution as a valid description of the stellar wind bow shock.
We also use the emission measure:
i.e., the square of the ion number density (
with
where
3. The Equation for The HII Region
For a star that emits S* ionizing photons per unit time, if the bow shock shell does not trap the ionization front, we will have a cometary HII region surrounding the stellar wind bow shock (see the schematic diagram of Figure 1). For a hypersonic flow, the ionization front limiting this HII region will not produce a hydrodynamic perturbation, and the environmental material will therefore flow with density ρa and velocity νa until it intercepts the bow shock (see Figure 1).
The equation determining the locus RIF (θ) of the ionization front is:
where the terms in the equation represent:
first term on the left: recombination in the region with radii Rb < R < RIF,
second left term: flux of neutrals entering the ionization front,
first term on the right: ionizing photon rate,
second right term: recombinations within the bow shock shell,
per unit time within the solid angle between θ and θ + dθ. In this equation, rIF = RIF sin θ is the cylindrical radius of the ionization front and αH is the H recombination coefficient (we set αH = 2.56 × 10−13cm3 s−1).
Combining equations (3-6) we obtain the dimensionless equation:
where Rb/R0 is given by equation (1),
is the Mach number of the impinging environment with respect to the isothermal sound speed of the photoionized gas,
is the Strömgren radius and
where
Our equation (7) is a generalization of equation (12) of Raga et al. (1997) (which has a dimensionless parameter ξ = χR0/Rs) to the case of a cometary HII region with an inner stellar wind bow shock producing an appreciable absorption of the stellar ionizing photons.
For θ = 0 from equation (7) we have:
where we have used the fact that G(0) = 3/2 (see equation A17). This is a cubic equation which can be inverted (analytically or numerically) to obtain the on-axis radius RIF,0 of the ionization front. This value can the be used to start a numerical integration of the ordinary differential equation (7) which then gives the shape RIF (θ) of the ionization front.
Depending on the values of the parameters χ, RS /R0 and Ma, we find that equation (11) has either:
This latter situation corresponds to the case in which the head of the bow shock traps the ionization front,
4. Numerical Results
As there is a considerable number of free parameters, a general exploration of the possible parameter space is lengthy (and also not very enlightening). We therefore choose to explore a limited range of parameters, which is appropriate for the case of a runaway O star passing through the plane of the Galaxy.
For the runaway O star, we choose a O7V star with wind velocity vw = 2500 km s−1, mass loss rate Ṁw = 4.5 × 10−7M⊙yr−1 and ionizing photon rate S∗ = 1049s−1. For the streaming environment we choose three possible velocities (va = 20, 100 and 300 km s−1) and four possible number densities (na = 1, 100, 104 and 106 cm−3). The values of R0, RS/R0 and χ corresponding to the chosen models are given in Table 1 (we do not list Ma = va /10 km s−1).
For the combinations of these environmental velocities and densities we first calculate the axial standoff distance RIF,0 of the ionization front from equation (11). The results of this exercise are given in Table 1. It is clear that for all of the chosen parameters the bow shock does not trap the ionization front, and that an external HII region is produced. The smaller HII region (relative to the size of the bow shock) is found for the va = 20 km s−1, na = 106 cm−3 model, in which the on-axis radius of the ionization front is 3 times the bow shock radius (see Table 1).
Table 1 Models for an O7 Star Passing Through the Galactic Plane
| va [km/s] | na [cm−3] | R0[pc] | RS/R0 | χ | RIF,0/R0 |
|---|---|---|---|---|---|
| 20 | 1 | 2.61 | 26.0 | 2.90 | 25.1 |
| 20 | 100 | 0.261 | 12.1 | 0.290 | 12.0 |
| 20 | 104 | 2.61e-2 | 5.60 | 2.90e-2 | 7.45 |
| 20 | 106 | 2.61e-3 | 2.60 | 2.90e-3 | 3.25 |
| 100 | 1 | 0.522 | 130.0 | 72.4 | 109.8 |
| 100 | 100 | 5.22e-2 | 60.35 | 7.24 | 58.0 |
| 100 | 104 | 5,22e-3 | 28.01 | 0.724 | 27.7 |
| 100 | 106 | 3.22e-4 | 13.00 | 7.24e-2 | 12.5 |
| 300 | 1 | 0.174 | 390.1 | 651.8 | 255.8 |
| 300 | 100 | 1.74e-2 | 181.1 | 65.18 | 161.8 |
| 300 | 104 | 1.74e-3 | 84.0 | 6.518 | 81.8 |
| 300 | 106 | 1.74e-4 | 39.0 | 0.6518 | 38.3 |
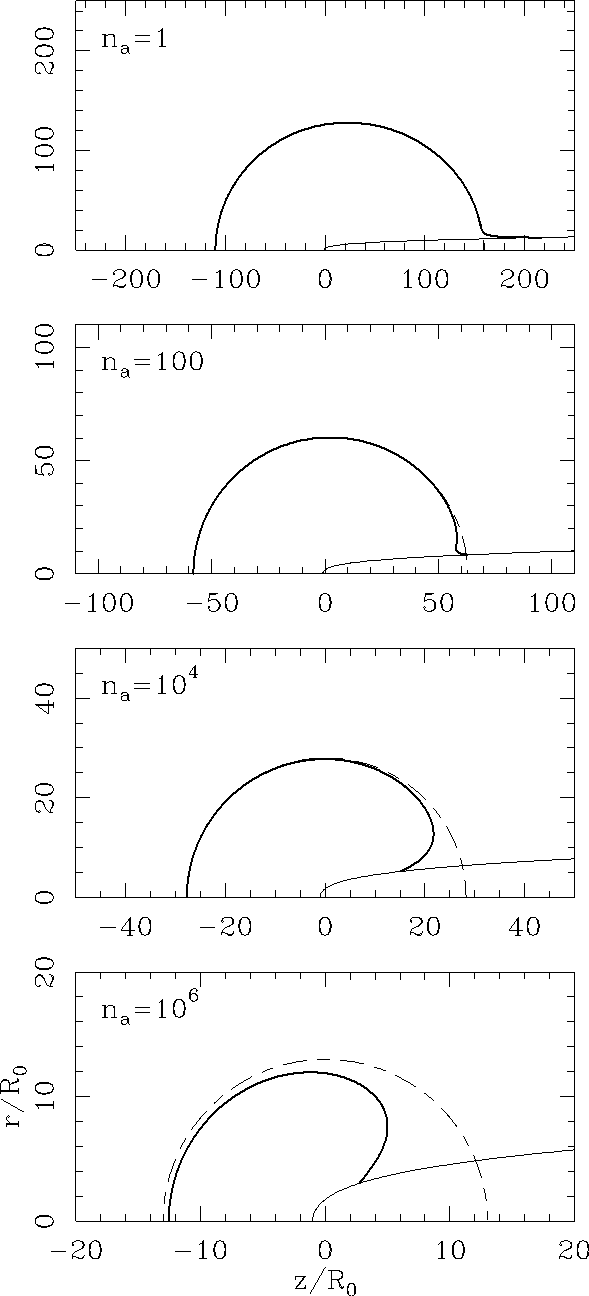
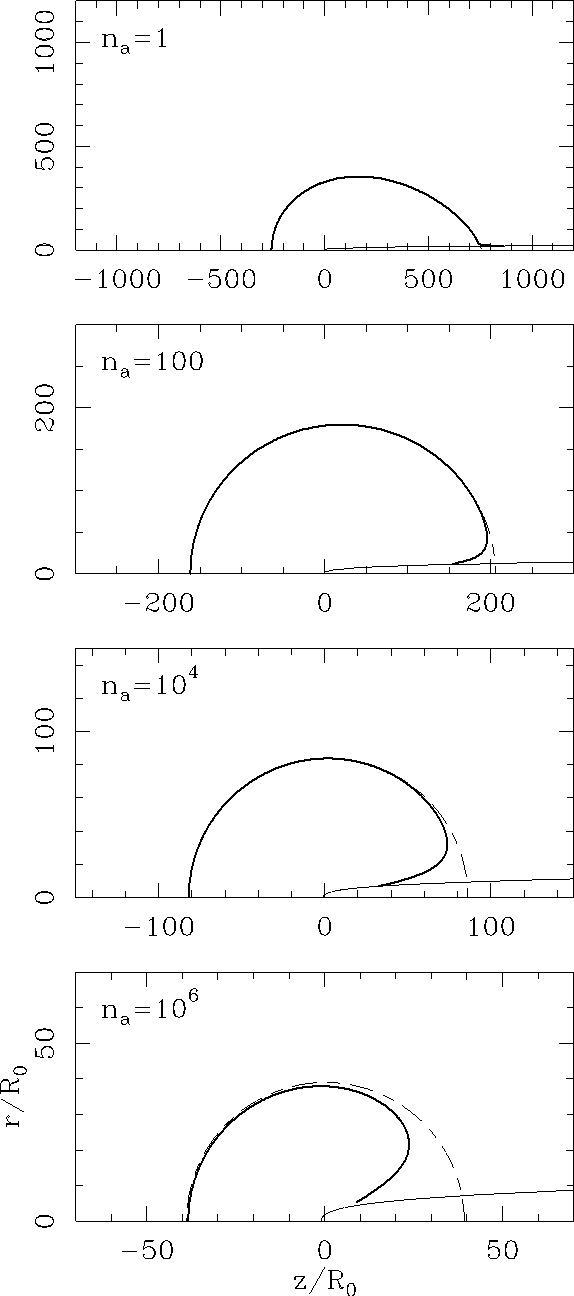
With the RIF (θ = 0) = RIF,0 initial condition, we integrate equation (7) to obtain the shape of the ionization front. The results for the va = 20 km s−1 models are shown in Figure 2, the ones for the va = 100 km s−1 models in Figure 3, and the results for the va = 300 km s−1 models in Figure 4,
Figures 2-4 show the stellar wind bow shock (equation 1), the ionization front RIF obtained from equation (7), and the ionization front RI obtained from equation (12) of Raga et al, (1997). RI is the ionization front that would be obtained for a star producing a S∗ ionizing photon rate, but with no wind (and therefore no stellar wind bow shock). Interestingly, in all but the va = 20 and 100 km s−1, na = 106cm−3 model, no difference can be seen in the leading hemisphere of the HII region (i.e., for z < 0).
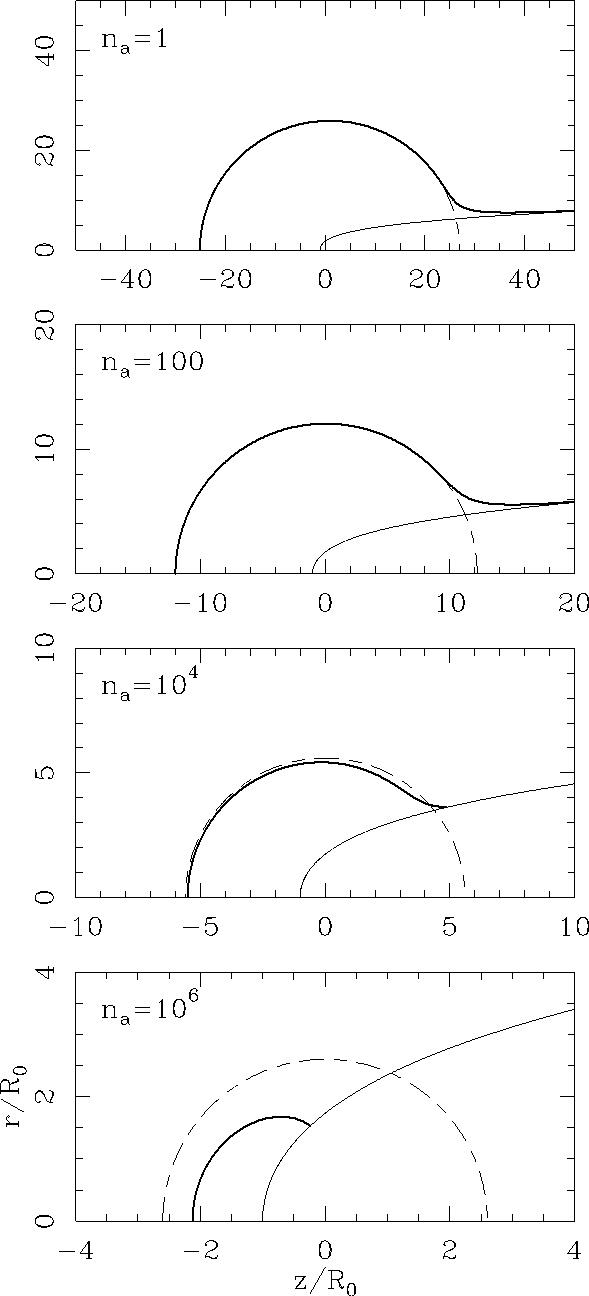
Fig. 2 The ionization front (thick, solid outer curve) and the stellar wind bow shock (thin, solid inner curve) obtained for models with va = 20 km s−1 and na = 1 (top frame), 100, 104 and 106 cm−3 (bottom). The dashed curves show the ionization front that would be obtained for a star with no wind. The (z, r) axes are given in units of R0.
Substantial differences between RIF and RI can be seen in the trailing hemisphere. The absorption of ionizing photons by the bow shock wings and the lack of absorption within the stellar wind region lead to the formation of either:
Except for the trailing region close to the bow shock wings, and except for the va = 300 km s−1, na = 1 cm−3 model (top frame of Figure 4, which has a clearly non-spherical HII region), the ionization front always has an almost spherical shape, with a radius close to the Strömgren radius RS for a star with S∗ in a stationary medium of density na (given in the fourth column of Table 1). The sphere, however, is not centered on the position of the star, but on a position downstream of the star. This effect is described by the “χ << 1 solution” of equation (13) of Raga et al. (1997), which to first order in χ corresponds to a sphere of radius RS centered on a point with a downstream offset of χR0/3 with respect to the position of the star.
5. Discussion
Our exploration of the parameter space for the interaction of a runaway O7 star with the surrounding ISM shows that there is:
a low density, high velocity regime (illustrated by our va = 300 km s−1, na = 1 cm−3 model, see the top frame of Figure 4) in which an elongated HII region with a tear-drop shape is formed, with a characteristic size of several hundred times the on-axis radius of the the stellar wind bow shock,
a high density, low velocity regime (illustrated by our vw = 20 km s−1, na = 106 cm−3 model, see the bottom frame of Figure 2) in which the photoionized environment is confined to a limited region around the head of the stellar wind bow shock,
an “intermediate” regime (shown by all of the other models, see Figures 2-4), in which the HII region is approximately spherical, with a radius ≈ RS and a small offset downstream from the stellar position, which intersects the stellar wind bow shock wings downstream of the star.
It is clear that we have not explored parameters for which the ionization front is trapped by the head of the stellar wind bow shock. Which parameters would be necessary for doing this? The condition for ionization front capture at the head of the bow shock can be obtained by setting RIF,0 = R0 in equation (11), which gives:
where RS is given by equation (9), R0 by equation (2), Ma by equation (8) and χ by equation (10) as functions of the physical parameters of the flow. If we fix the stellar parameters for an O7V star, the remaining free parameters are the density and velocity of the streaming environment. Equation (12) then gives us the minimum environmental density na,c as a function of velocity va necessary for the ionization front to be captured by the head of the bow shock. The results of this exercise are shown in Figure 5.
We see that for the va = 1 → 40 km s−1 range shown in Figure 5, the critical density is in the na,c ∝ va1/2 regime obtained from equation (12) for << χ 1. It is clear that for va 1 km s−1, large environmental densities are required in order for the bow shock to capture the ionization front!
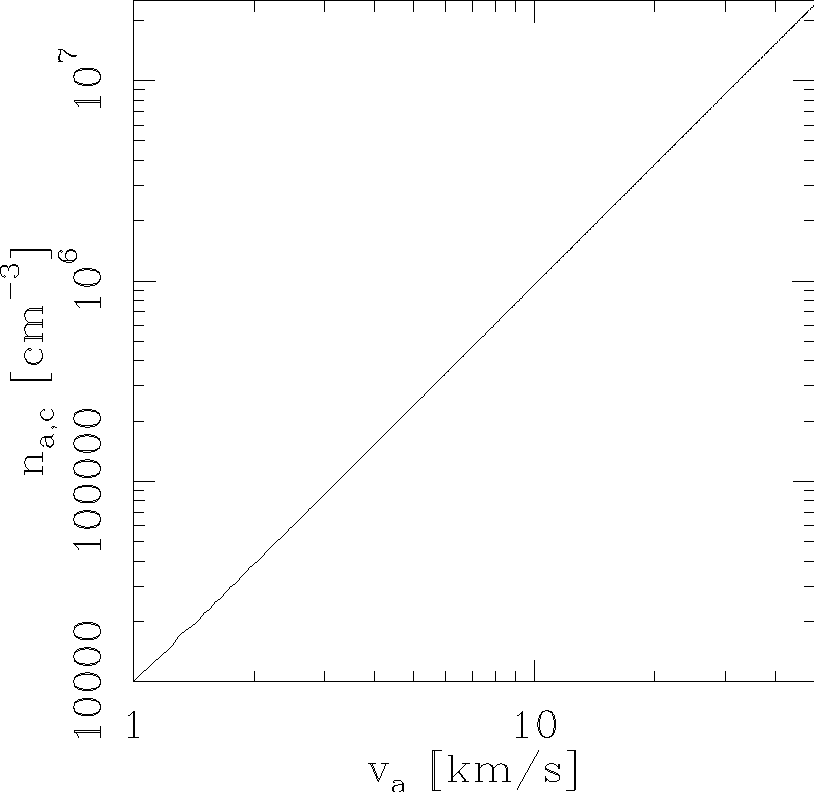
Fig. 5 Minimum environmental density na,c (for capturing the ionization front) as a function of velocity va for the parameters of an O7V star (see the text).
For va >10 km s−1 stellar motions, na,c >107 cm−3 environmental densities are required, so that it is unlikely that one will ever find such objects with ionization fronts captured by the stellar wind bow shocks. For lower values of va, one could have captured ionization fronts provided that the objects travel within a dense molecular cloud (of densities ≈ 105 → 107 cm−3, see Figure 5).
We are, of course, now talking about compact/ultracompact HII regions within dense molecular clouds, produced by massive stars with velocities of a few km/s with respect to the surrounding cloud. Interestingly, as we see in Figure 5, we could also have O stars with va = 1 → 10 km s−1 with bow shocks that do not capture the ionization fronts. This parameter regime is interesting because it is not correctly described by our present model.
For va < 10 km s−1, the steady bow shock+HII region configuration (for a case in which the IF is not captured by the bow shock) will have a motion through the neutral environment that is subsonic with respect to the c0 ≈ 10 km s−1 isothermal sound speed of the ionized gas. Such an ionization front will have a strong hydrodynamical effect, driving a shock wave ahead of it into the neutral environment. The post-shock material will be almost at rest with respect to the star, and therefore will not shock again before reaching the contact discontinuity against the stellar wind.
The flow configuration will then have an inner shock involving the stellar wind, and an outer shock surrounding an extended HII region. This outer bow shock will be somewhat peculiar, since all of the post-shock flow (even far along the bow shock wings) will be subsonic (because the pre-shock flow is subsonic with respect to c0). Therefore, the post-bow shock flow will not have the typical division between a compact axial subsonic region and an extended supersonic region farther away from the flow axis.
In a future paper we will continue with a study of this interesting regime (already explored by Arthur & Hoare 2006) with axisymmetric gasdynamic+radiative transfer simulations. Clearly, the codes needed to do this have already been fully developed (see, e.g., Mackey et al. 2021).











 nova página do texto(beta)
nova página do texto(beta)