1. INTRODUCTION
The gravitational interactions due to a compact object moving through an environment were first studied by Bondi & Hoyle (1944). These interactions result in the deviation towards the symmetry axis of the streaming environment, and the formation of a “tail” of material behind the compact object (part of which ends up accreting onto the object). This flow is now called “Bondi-Hoyle (B-H) accretion”, and the trail of perturbed material left behind by the moving object is the “B-H tail”.
Most of the studies of B-H accretion have concentrated on evaluations of the gravitational drag on the compact object (see, e.g., Dokuchaev 1964; Ostriker 1999; Sánchez-Salcedo 2009; Cantó et al. 2011; Lee & Stahler 2014). This problem has recently gained interest in the context of planets within accretion disks. Some of the relevant papers are:
Cantó et al. (2013): a model for the drag on a point source within a disk with a Gaussian vertical density profile
Thun et al. (2016): axisymmetric simulations from which they calculate the total hydrodynamic+gravitational drag on a rigid sphere,
Masset & Velasco Romero (2017) and Velasco Romero & Masset (2020): show that radiative heating from emission of a point source can have strong effects on the gravitational drag.
In the present paper, we focus on the dynamics of the B-H tail left behind by a high velocity, compact object. This tail, seen in numerical simulations of hypersonic compact objects moving through a dense, highly radiative medium (see, e.g., Cantó et al. 2011) is formed by the convergence of the streaming environment onto the axis defined by the motion of the compact object.
Under the assumption of a locally well mixed flow, we derive the equations for the motion of the flow along the B-H tail, and derive a full numerical solution and an approximate analytic solution of the velocity and mass distribution of the tail (§ 2). We then study a time-dependent problem of the B-H tail left behind by compact object which first travels within a dense cloud, and then emerges into a low density environment (§ 4). The applicability of the B-H tail model to different kinds of compact objects is then discussed (§ 5). A discussion of the strong cooling assumption in our analytic model is presented in § 6. Finally, the results are summarized in § 7.
2. The steady B-H tail
2.1. The Free-Streaming Trajectories
Let us consider a point mass M located at the origin of an xy-coordinate system, immersed in a hypersonic flow impinging along the x-axis, which is homogeneous and has a velocity v 0 for x → -∞. This situation is shown in the schematic diagram of Figure 1.
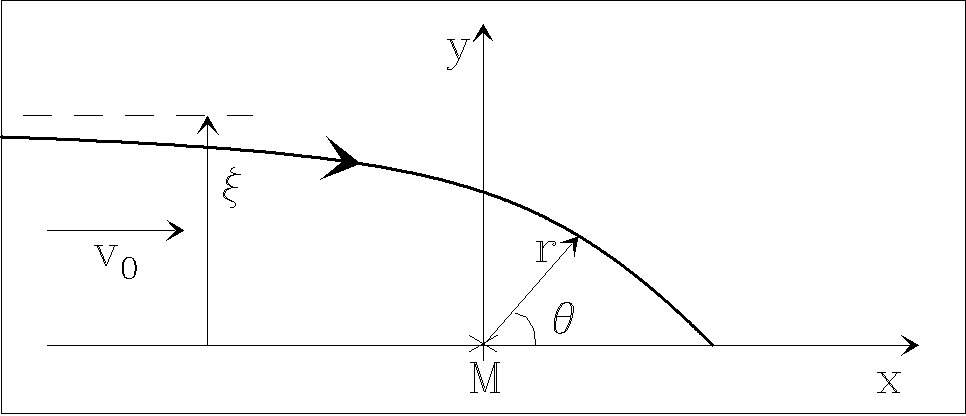
Fig. 1 Schematic diagram showing a plane flow travelling in the +x direction with a velocity v 0, which is perturbed by the gravitational attraction of a point source of mass M located at the origin of the xy-coordinate system. The thick curve shows the trajectory of a free-streaming fluid parcel with an initial impact parameter ξ
A fluid parcel impinging with an initial impact parameter ξ will follow the free-streaming trajectory
where
G is the gravitational constant, θ the angle measured from the x-axis and r the spherical radius (see Figure 1).
The components of the velocity of the fluid parcel along this trajectory are:
The flow parcels with impact parameter ξ then intersect the x-axis at a position
with an axial velocity
A more detailed derivation of these equations is given by Cantó et al. (2011).
The flow parcels arriving at the x-axis join a turbulent B-H tail into which they feed mass and momentum. This is described in the following subsection.
2.2. Mass and Momentum Fed into the B-H Tail
Let us consider the mass fed at position x in an interval Δx along the B-H tail. From equation (4) we obtain the range of impact parameters
of the flow parcels that arrive onto the axis inside Δx.
As the impinging flow is homogeneous (of density ρ0), the mass injection rate of the flow parcels within the Δξ impact parameter range is:
Combining equations (4), (6) and (7) we then obtain the mass rate fed per unit length into the tail:
which is independent of the position x along the tail. From equations (5) and (8) we find that the momentum injected per unit length into the tail is simply
2.3. The Equations of Motion for the B-H Tail
The mass σ per unit length along the B-H tail satisfies continuity and momentum equations of the form:
where v is the velocity along the B-H tail. In these equations we have considered the mass and momentum rates injected by the material accreting onto the tail (equations 8 and 9) and the gravitational force of the perturber. We have also neglected the pressure force along the axis of the B-H tail, as appropriate for a flow with strong radiative cooling.
We now define the dimensionless variables
with ξ0 given by equation (2) and
In terms of these dimensionless variables, equations (10-11) take the form:
in which the terms representing the mass and momentum incorporation into the tail take a unitary value.
2.4. The Stationary Case
The equations for a stationary B-H tail are obtained by setting the time derivative in equations (14-15) to zero, giving:
Equation (16) can be integrated to obtain:
where x'0 (an integration constant) is the position along the tail which separates a negative velocity region (for x´<x'0, of material accreting onto the point mass) from a positive velocity region (for x´>x'0, with tail material that escapes from the point mass).
Combining equations (17-18) we obtain a differential equation involving only the velocity:
This equation has a critical point at [x´=x'0, v´0], in which both the numerator and denominator of the right hand term are zero. The desired critical solution has to go through this critical point, smoothly joining the accreting x´<x'0 region and the escaping x´>x'0 region.
One can find the value of σ’ at the critical point by first taking the x’→x’0 limit of equation (18):
and in this limit equation (19) becomes:
We therefore obtain:
We have been unable to find analytical expressions for the position x’ 0 of the critical point nor for the v’(x’) solution of equation (19), and therefore proceed numerically. There are two standard options for finding critical solutions numerically:
with a shooting method, in which successive integrations (of equation 19) starting at a small x’ (integrating in the +x’-direction) and at a large value of x’ (in the -x’-direction) are calculated with different initial v’ values, until two solutions with a good match at the critical point are found,
integrating the time-dependent equations (in our case, equations 14-15) and letting them relax to the stationary solution.
We have chosen this second possible approach. We integrated the time-dependent equations (14-15) with a simple, finite-difference method, starting with a (σ’ = 10-3, v’ = 0) uniform initial condition. It would be more natural to choose a σ’ = 0 initial condition (corresponding to a B-H with no initial mass), but this is unsuitable for carrying out the first integration step of the finite-difference method. We find that for a dominion of spatial extent x’max, at a time t’relax ≈ x’max, the solution converges to a stationary solution. We therefore integrate for a time =10x’max to guarantee convergence.
The stationary solution obtained in this way is shown in Figure 2. We find that the critical point at which the flow velocity goes from negative to positive velocities is located at x’0 ≈ 1.51. At this point, the density is σ’ = 2.19. These values of x’0 and σ’0 approximately satisfy equation (22).
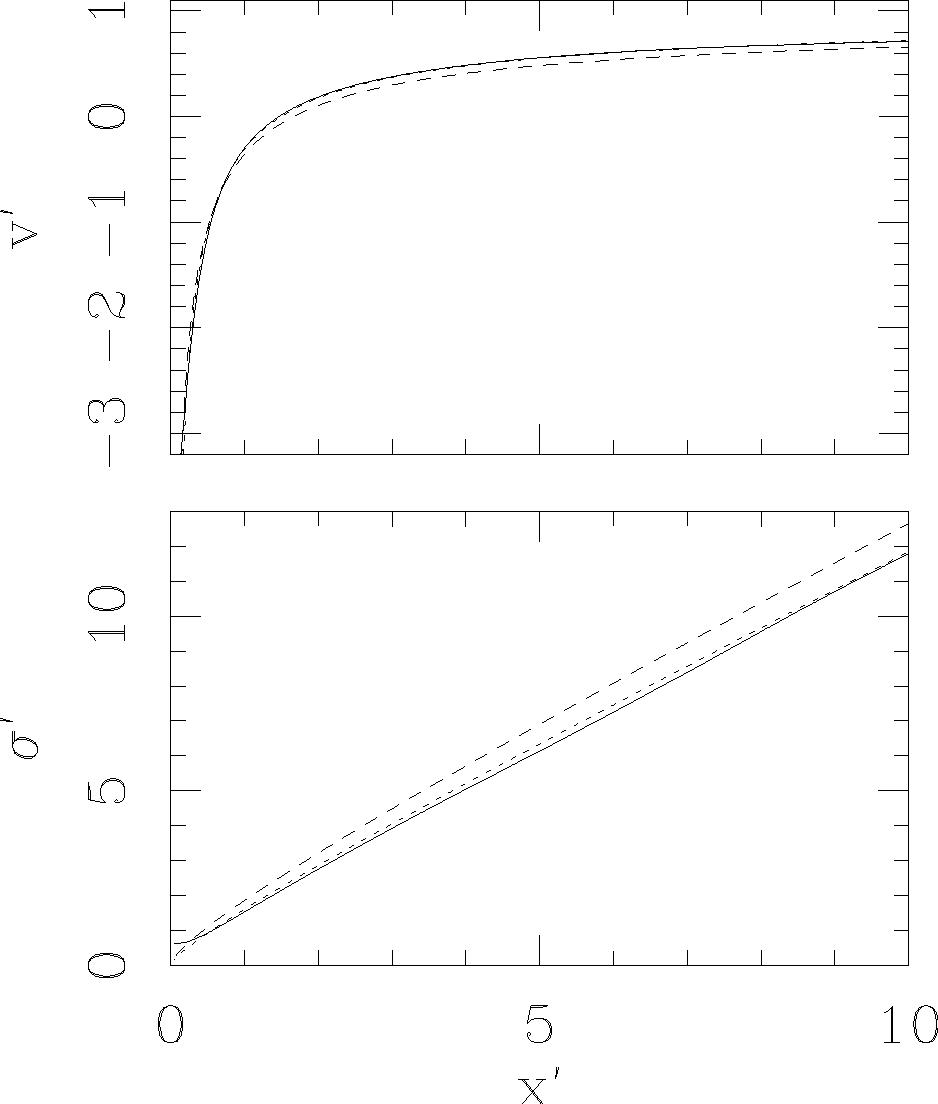
Fig. 2 Stationary solution for the dimensionless velocity v' (top) and mass per unit length σ' (bottom) as a function of dimensionless distance x' of the flow along a B-H tail. The solid lines correspond to the numerical solution, and the (barely distinguishable) short dash lines to the analytic approximation of equations (23-24). The long dash lines show our second analytic approximation given by equations (25) and (30).
We find that the v’(x’) stationary solution (obtained numerically, see above) can be well reproduced with a simple, single parameter fitting function of the form
with the x’ ≈ 3/2 of the numerically determined critical point. The corresponding approximation for the dimensionless density σ’ can then be calculated from equation (18), obtaining:
The analytical approximations of equations (23-24) with x’0 = 3/2 are shown in Figure 2.
We now present a purely analytic derivation of a similar approximate solution. This is done as follows:
a. We consider a fitting function of the form:
with arbitrary constants x’0 and β,
b. From this equation we compute the first and second derivatives with respect to x’ at position x’0:
c. And then obtain the first and second derivative of v’(x’) at x’= x’0 from equation (19) and its x’-derivative:
d. Finally, equating (26) to (28) and (27) to (29) we obtain:
The resulting v’b (x’) (obtained substituting the values of equation 30 in equations 23 or 25) is shown in Figure 3. We see that it is a reasonable approximation for the numerically obtained v’(x’), but it is less accurate than the x’0 = 3/2 fit to the numerical results (see above and Figure 2).
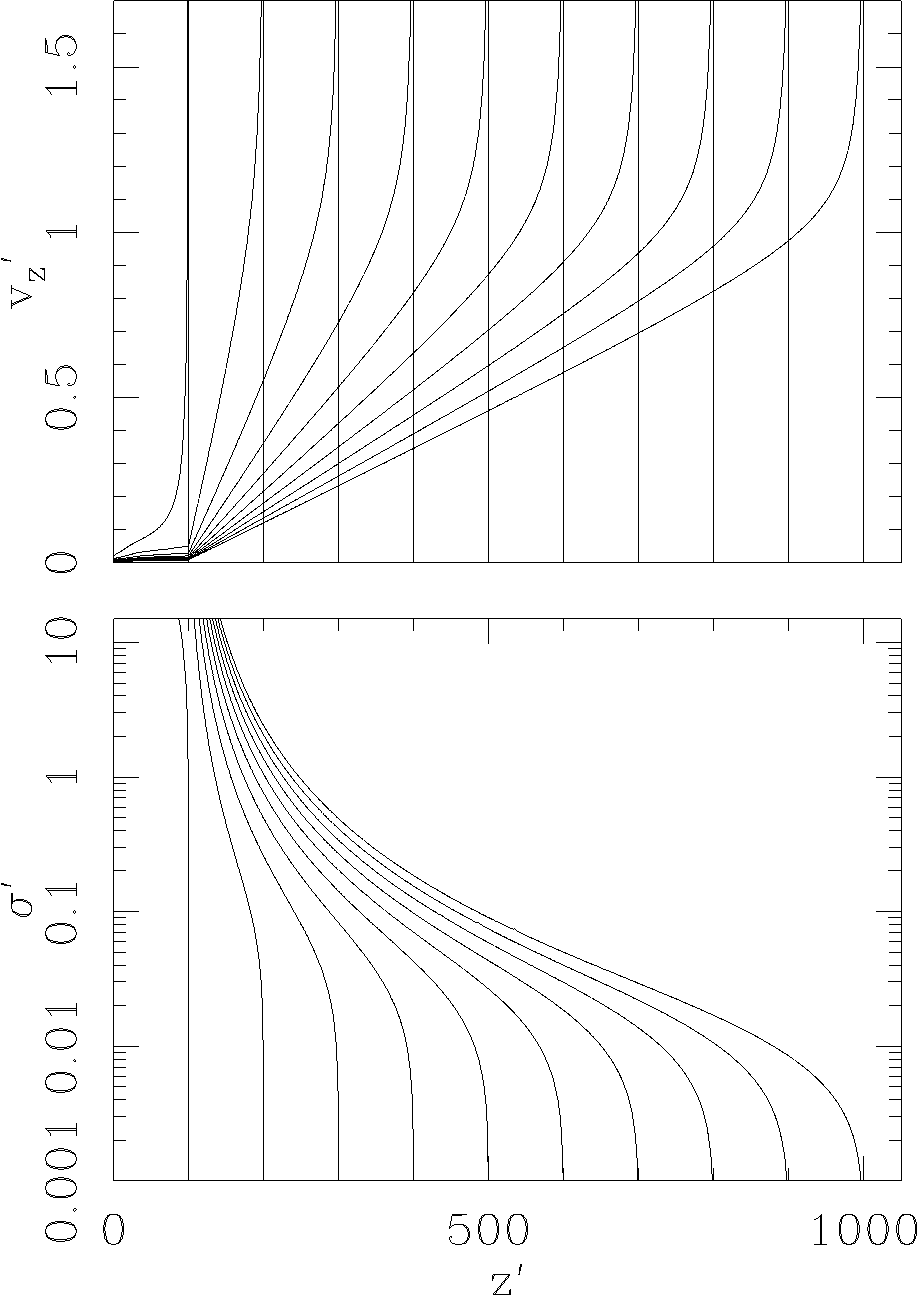
Fig. 3 Dimensionless velocity (top) and mass per unit length (bottom) as a function of distance (in a reference frame at rest with respect to the environment) for the time-dependent B-H tail produced by a point mass that emerges from a dense cloud (in the z' < 100 region) into a low density environment (for z' > 100). The left curves correspond to a time t' = 100, and the right curves to t' = 1000, with the successive curves at ∆t' = 100 intervals.
3. Point mass emerging from a dense cloud
Let us now consider the problem of the B-H tail produced by a point mass that first travels within a dense environment, and then suddenly emerges into a very low density environment. This situation can be modeled using equations (14-15) for the region of the flow within the dense cloud, and with similar equations with no mass/momentum deposition (i.e., setting to zero the unitary terms on the right hand side of equations 14-15).
We have carried out a numerical integration in which a dense environment of density ρ0 (with which we normalize the equations, see equation 13) impinges on the point mass for a time t’0 = 100 (corresponding to a displacement x’0 = 100 of the point mass with respect to the environmental gas), followed by a zero density impinging environment for t’ > t0. The chosen value for t’0 allows an approximately stationary B-H tail to develop behind the point mass.
We plot the results in a reference system that is at rest with respect to the environmental gas. We therefore use z’ = t’ - x’ as spatial coordinate (with the point mass travelling in the +z' direction) and a velocity v'z = 1 - v'.
The results obtained from the simulation are shown in Figure 3. In this Figure, we show the velocity v'z and the mass σ’ along the B-H tail as a function of z' at time intervals Δt’ = 100. The first curves (with the shortest z’ extensions) correspond to t’ = 100 (i.e., the moment at which the point source emerges from the edge of the dense cloud, at a position z’ = 100, see above), and the most extended curves correspond to t’ = 100.
The velocity distributions show a high peak close to the positions of the point mass, which correspond to the v’ → -∞ material accreting onto the compact object. This region of high v’z has very low mass per unit tail length σ’ (as can be seen comparing the top and bottom frames of Figure 3).
In the region from the point of emergence from the cloud (at z’ = 100, see above) to the point with v’z ≈ 1 the B-H tail develops a linear ramp of increasing velocities (top frame of Figure 3), due to a “velocity sorting” of the material in the free (x’ > x’0) region of the tail. This “Hubble velocity law” region has a mass σ' that rapidly drops for increasing z’ values.
Through the velocity sorting mechanism, the B-H tail generated by the point mass when it was within the “dense cloud region” (i.e., in the z’ ≤ 100 region) at later times becomes very extended (e.g., from z’ → 1000 for t’ = 1000), and might be easier to resolve with limited resolution observations. This long tail has a total mass that is somewhat smaller than the mass that is dragged out from the dense cloud, as part of the B-H tail is accreted onto the point mass.
4. Applicability of the model
Let us now consider the nature of the “point mass” producing a B-H tail. The clear candidate for producing this flow would be a black hole or a neutron star. Also, runaway compact objects from planets to different types of star could in principle produce B-H tails under the conditions that are discussed below.
The region of the B-H tail following the motion of the source is produced by material with impact parameters ≤ ξ0 (see equations 1-2). Therefore, for this region of the tail to be formed the condition R* < ξ0 (where R* is the radius of the source) has to be satisfied. Combining this condition with equation (2) we then see that the velocity v0 of the source relative to the environment must satisfy the condition:
Table 1 gives estimates of vmax for a selection of planets, main sequence stars and compact stars (a white dwarf and a neutron star). It is clear that an Earth-like planet will develop a B-H tail only if it is travelling at a velocity < 8 km s-1, and a “Jupiter” at velocities < 40 km s-1 with respect to the surrounding environment.
Table 1 Maximum Velocity and Minimum Environmental Densities for Different Objects
| Earth | Jupiter | Sun | O7V | White dwarf | Neutron star | |
|---|---|---|---|---|---|---|
| M[M⊙] | 3.0 x 10-6 | 9.5 x 10-4 | 1.0 | 40 | 1.0 | 1.5 |
| R* [R⊙] | 9.2 x 10-3 | 0.10 | 1.0 | 10 10-2 | 1.4 x 10-5 | |
| Ṁ[M⊙/yr] | … | … | 3.0 x 10-14 | 10-6 | … | 2 x 10-11 |
| vw [km/s] | … | … | 400 | 2500 | … | ~3 x 105 |
| vmax [km/s] | 7.9 | 42 | 440 | 880 | 4400 | 1.4 x 105 |
| nc [cm-3] | … | … | 1.6 x 104 | 2.1 x 109 | … | 0.3 |
If the source of the B-H tail has a stellar wind, we will have a wind/environment bow shock of characteristic size
where vw and Ṁ are the terminal velocity and the mass loss rate (respectively) of the stellar wind. The bow shock will deflect the environmental material with impact parameters < Rbs, so for the inner part of the B-H tail to be formed, the condition ξ0 > Rbs has to be met. For a star (with vw, Ṁ) moving at a velocity v0, we then need an environmental density
where in the right hand term have set Rbs = ξ0 (see equation 2) in equation (32).
In Table 1 we give the minimum number densities nc = ρ0/(1.3mH) (where mH is the hydrogen mass and we assume a 10% He abundance) obtained for a source velocity v0 = 100 km s-1. We see that a “halo population” solar type star passing through the plane (with typical velocities ≈ 100 km s-1 with respect to the galactic plane IMS), will only form a B-H tail when going through a particularly dense region (e.g., a molecular cloud) of n > 104 cm s-1. On the other hand, because of its strong stellar wind, a runaway O star will never develop a B-H tail, as the required environmental densities for confining the bow shock are too high (see Table 1).
Clearly, the best potential candidates for producing observable B-H tails are white dwarfs and neutron stars (see Table 1). A standard white dwarf does not have a detectable wind, and a neutron star could have an appreciable relativistic wind (as implied by some of the observed pulsar wind nebulae, see, e.g., Kargaltzev & Pavlov 2007). However, a relatively low density environment should be able to confine this wind (see the last row of Table 1). Of course, a black hole (not included in Table 1) will produce a B-H tail even if it is travelling at relativistic velocities.
5. The strong radiative cooling approximation
In this section we discuss under which conditions there is strong radiative cooling in the B-H tail. In our solution, the characteristic size of the flow both across and along the symmetry axis is ξ0 (see equation 2). The condition for radiative cooling to be important is that the cooling distance dcool behind the shock (through which the material enters the shock) has to be smaller than ξ0. In the dcool ≈ ξ0 limit, we will have a tail of radius also ≈ ξ0.
If the cross section of the tail has a cylindrical radius ≈ ξ0, the material (of impact parameter ≈ ξ0) entering the tail goes through a shock of velocity ≈ v0 (see equation 3) and preshock density ≈ n0 (see equation 8). The cooling distance behind this shock can be estimated using plane-parallel shock models. A possible analytic fit to the cooling distances of the conveniently well tabulated shock models of Hartigan et al, (1987) is:
appropriate for the v0 = 20 → 400 km s-1 shock velocity range.
Now, setting dcool = ξ0 and using equations (2) and (34), we find an estimate for the minimum environmental density ncool for which the material in the Bondi-Hoyle tail has substantial cooling:
In Figure 4, we give ncool as a function of v0 for a 1 M⊙ point mass source. We see that for a 1 M⊙ object travelling at a ≈ 100 km s-1 velocity, an environmental density of at least ≈ 105 cm-3 is necessary for the B-H tail to be radiative.
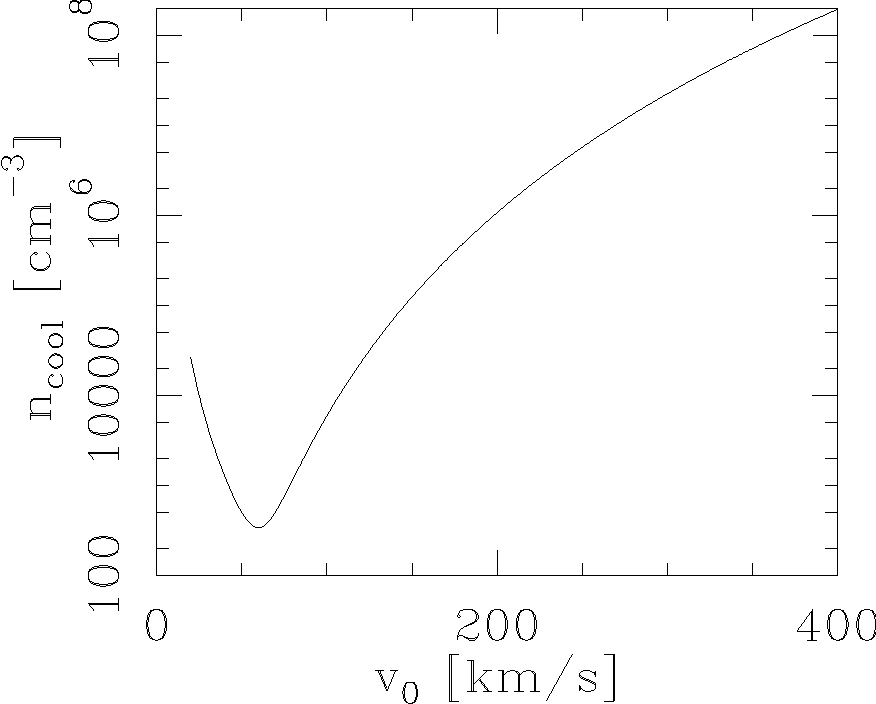
Fig. 4 Minimum environmental number density ncool for producing a radiative, B-H tail as a function of the velocity v0 of motion of a one solar mass point source. The density scales as the inverse of the mass of the point source (see equation 35).
If this condition is not met, the tail will not be radiative, and the tail solutions of sections 2 and 3 are strictly not applicable. However, when comparing “thin flow solutions” (such as our present B-H tail solution) with numerical simulations, one finds that even for the case of non-radiative flows (in which the flow interaction regions are not narrow) the thin-flow solutions are still a reasonable approximation. This is the case, e.g., for stellar wind bow shocks (see, e.g., Raga et al. 1987). Further work will have to be done to see to what extent our present B-H tail analytic model agrees with non-radiative gas dynamic simulations.
6. Summary
We have presented a model for the dynamics of the dense tail of material left behind by a point mass in hypersonic (but non-relativistic) motion with respect to the surrounding environment. Under the assumptions of ballistic motion for the environment (before entering the tail) and locally well mixed material along the tail, the steady state is described by a quite simple differential equation (see equation 19).
We have been unable to find a full analytic solution for the steady B-H tail. However, we have numerically integrated the time-dependent equations to achieve the steady state (and therefore avoid finding the position of the critical point with a shooting method). We also find approximate analytic solutions that agree well with the numerical results.
We then studied the time-dependent problem of a B-H tail developed in the passage of the point source within a dense environment, followed by the emergence of the source into a very low density environment. This flow results in an extended “velocity sorted” (linear velocity vs. position) region of dragged out material joining the emerged source to the dense cloud.
Both of the solutions described in this paper have a constant velocity v0 for the source. This, of course, limits the models to cases in which the perturbed environmental mass is small relative to the source mass. Clearly, it would be also possible to study cases in which the gravitational drag and the accretion modify the velocity of the source.
In order for the B-H tail to be produced, the motion v0 has to be slower than the escape velocity from the surface of the source (as otherwise the source itself will directly accrete or displace the material that would form the tail, see section 4). Clearly, this does not introduce strong constraints on the motion in the case of neutron stars (with relativistic escape velocities) or black holes, but is an important limit for planetary or stellar sources.
Also, if the source has a stellar wind, it will produce a cometary bow shock that can stop the formation of the B-H tail. For a given motion v0, one can calculate the minimum value of the environmental density ρ0 for which the bow shock will be confined to a small enough size. This condition implies high environmental densities (such as would be found in dense molecular clouds) in order for main sequence stars to be able to form B-H tails, We note that at least some pulsars have quite substantial relativistic winds (see, e.g., the review of Kargaltsev et al. 2017). However, these winds would be confined by relatively low density environments (see § 4).
We leave our model without a direct application to observed objects. It should be considered as a possibility for modelling runaway compact objects followed by trails of emitting gas, possibly joining them to a dense cloud from which they have emerged. We will explore different possible objects in a future study.











 nueva página del texto (beta)
nueva página del texto (beta)


