1.Introduction
Collimated ejections from stars sometimes show high velocity clump structures which are joined to the source by a fainter emitting region with a “Hubble velocity law” of increasing radial velocities with distance. This type of structure is seen in some planetary nebulae; examples are described by Alcolea et al. (2001) and Dennis et al. (2008).
There is also the remarkable “Orion fingers” multiple outflow from the Orion BN-KL region (e.g, Allen & Burton 1983; Zapata et al. 2011; Bally et al. 2017). This outflow has ≈100 collimated features radiating away from the BN-KL multiple stellar system. These features have CO emission with Hubble law, linear radial velocity vs. position structures, ending in compact clumps (seen in H2 and optical atomic/ionic lines). Rivera-Ortíz et al. (2019a, b) have modeled these structures as dense clumps travelling semi-ballistically away from the source region.
In a recent paper, Raga et al. (2020) have presented a model for a “single pulse ejection” jet, which results in the production of a dense “head” joined to the outflow source by a “tail” which develops a linear, Hubble law velocity structure for times greater than the duration of the pulse. This “head/tail plasmon” flow is clearly promising for modelling the objects described above.
Raga et al, (2020) studied the problem of a collimated flow produced by a parabolic, single pulse ejection velocity variability. They also assumed the mass loss rate to be time-independent during the duration of the pulse (so that the ejection density is proportional to the inverse of the ejection velocity). With these assumptions, they obtained a fully analytic model, and also presented an axisymmetric numerical simulation of the flow.
In the present paper, we extend the work of Raga et al. (2020) to a different functional form for the ejection velocity pulse, which we now assume to have a Gaussian time-dependence. We also study two different forms for the ejection density history: a time-independent density, and a Gaussian density history (with the same time-width as the velocity pulse).
The paper is organized as follows. In § 2 we describe the time and position for the formation of the leading working surface of the flow. In § 3 we describe the method for determining the motion of the leading working surfaces, and apply it to the case of constant ejection density. The solutions obtained for different values of the environment to outflow density ratio are presented in § 4. Solutions for the case with a Gaussian ejection velocity variability are presented in § 5. The velocity and density structures of the tails (for the Gaussian plasmons with constant and with Gaussian ejection density histories) are modeled in § 6. Finally, the results are summarized in § 7.
2.The Formation of a Working Surface
In regions without shock waves, a 1D, hypersonic jet flow follows the free-streaming solution
where u (x,t) is the velocity (along the outflow axis) as a function of distance x from the source at an “evolutionary time” t, τ is the “ejection time” at which the fluid parcel at position x was ejected, and uo(τ) is the velocity with which it was ejected.
From equation (1), one can straightforwardly derive the relation:
where
We now propose a Gaussian form for the ejection velocity:
where τ0 is the dispersion and v0 the peak velocity, The time for the formation of a discontinuity (equation 3) is then:
It is clear that for the flow ejected at large negative times the formation of a discontinuity occurs at a time
As discussed, e.g., by Raga et al. (1990), the discontinuities formed by an ejection velocity variability in a hypersonic jet correspond to two-shock “working surfaces”. The motion of the “head” (leading working surface) of the flow produced by a Gaussian ejection velocity pulse is described in the following section. The region between the head and the outflow source is filled by material from part of the decreasing velocity wing of the ejection velocity pulse (see the schematic diagram of Figure 1).
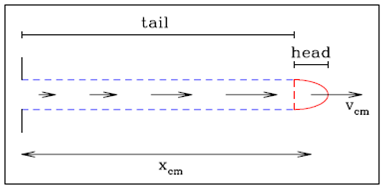
Fig. 1 Schematic diagram showing the structure of a “head/tail plasmon” produced by a single pulse ejection velocity variability. The rising velocity wing of the ejection pulse piles up into the leading head, and part of the decreasing velocity wing fills up the region between the head and the outflow source. The color figure can be viewed online.
3.The Motion of the Plasmon Head
Under the assumption of a cylindrical flow, the position xcm of the center of mass of the material that has entered the working surface at the head of the plasmon (see equation 1 of Raga et al. 2020) is given by:
where
and the integration limit τ is the root of:
Following Cantó et al. (2000) and Raga et al. (2020), instead of inverting equation (8), we will use τ (i.e., the ejection time) as independent variable, and find xcm (from equation 6) and the evolutionary time t (from equation 8) as a function of τ.
We now consider a Gaussian ejection velocity variability (see equation 4), a constant ejection density p0 and a uniform ambient density pa. Equation (6) then takes the form:
where
and
is the error function.
From equations (9-10) we obtain the quadratic equation for xcm:
with
4.Solutions for Different σ Values
4.1.The 𝛔 = 0 “Free Plasmon”
The σ parameter is the ratio between the environmental and ejection densities, multiplyed by a factor of order one (see equation 13). For the “free plasmon”, σ → 0 case, equation (12) has the solution:
Numerically, we find that the denominator → 0 as
and then xcm →∞ at τ = τ a . This result implies that none of the material from the τ > τc wing of the ejection pulse (see equation 4) ever reaches the working surface. Therefore, the leading head has to asymptotically approach a velocity
Using the appropriate integrals from equation (10), we find that the mass of the plasmon as a function of τ is:
where M0 is the mass of the ejection pulse. Evaluated at τ a (see equation 17) we obtain an asymptotic mass Masym = 0.753M0.. In other words, ≈ 75% of the mass of the pulse is incorporated into the head of the plasmon, and ≈ 25% remains in the “tail” that joins the outflow source and the head.
4.2.Solutions for σ > 0
For σ > 0, the position xcm of the head of the plasmon can be straightforwardly obtained by inverting equation (9), and evaluating the integrals (see equation 10) as a function of the ejection time τ. Also, calculating the evolutionary time t as a function of τ (see equation 8), we can obtain xcm(t). Doing the appropriate time derivatives (analytically or numerically), we can also obtain the velocity vcm = dxcm/dt of the plasmon head.
The results obtained for different values of σ are shown in Figure 2. It is clear that for σ = 0 the plasmon reaches the asymptotic velocity v a (see equation 18). For σ >0, vcm, reaches a maximum value and then decreases as a funciton of time as the plasmon head incorporates more environmental material.
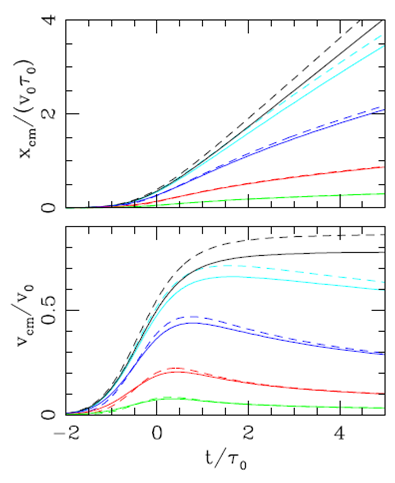
Fig. 2. Dimensionlessposition (top) and velocity (bottom) of the plasmon head as a function of evolutionary time for σ = 0 (black curve), 0.1 (cyan), 1.0 (blue), 10 (red) and 100 (green). The solid curves show the results for the constant ejection density problem, and the dashed curves show the Gaussian ejection density case (with σ1 values equal to the σ values given above). The color figure can be viewed online.
For σ > 0, the head of the plasmon has a mass given by the contribution from the ejection pulse (see equation 19) and also a contribution from the environment:
where M0 is the mass of the ejection pulse and σ is given by equation (13).
The mass in the tail (i.e., in the continuous beam segment between x = 0 and xcm) is:
In Figure 3 we plot the mass Mt of the tail, the total mass Mh = Mp + Ma of the plasmon head and the fraction M a /Mh of this mass that corresponds to the swept-up environment as a function of the evolutionary time t for models with different σ values.

Fig. 3 Dimensionless mass (top) of the “constant density plasmon” head Mh (solid curves) and tail Mt (dashed lines), and fraction of environmental mass within the head (bottom). The results obtained for models with σ = 0 (black curves), 0.1 (cyan), 1.0 (blue), 10 (red) and 100 (green) are shown. The color figure can be viewed online.
5.The Case of a Gaussian Ejection Density Variability
Let us now consider an ejection with a Gaussian velocity variability (see equation 4) and also with a Gaussian density variability:
of the same shape. In this equation,
Inserting the ejection velocity (equation 4) and density (equation 22) variabilities into equation (6), we obtain an equation of the same form as (9), but with
Combining equations (9) and (23), we obtain the quadratic equation for xcm:
with
The position xcm and velocity dxcm/dt as a function of 𝑡 obtained for different σ1 values are shown in Figure 2. It is clear that for all σ1 values, the plasmon head is faster than the “constant density plasmon” with σ = σ1 (see equations 13 and 25). For σ1 = σ > 0, the “Gaussian density” and “constant density” plasmons converge to the same velocity for t >> τ0.
Also, using the appropriate integral from equation (23), we find that the contribution from the ejection pulse to the mass of the plasmon head as a function of τ is:
where M0 is the mass of the ejection pulse. The mass in the tail (i.e., in the continuous beam segment between x = 0 and xcm) is:
The head of the plasmon has a mass given by the contribution from the ejection pulse (see equation 28) and a contribution from the environment:
where M0 is the mass of the ejection pulse and σ1 is given by equation (25).
In Figure 4 we plot the mass Mt,1 of the tail, the total mass Mh,1 = Mp,1 + Ma,1 of the plasmon head and the fraction Ma,1/Mh,1 of this mass that corresponds to the swept-up environment as a function of the evolutionary time t for models with different σ1 values. The results are qualitatively similar to the ones obtained for the constant ejection density plasmon (see Figure 2).
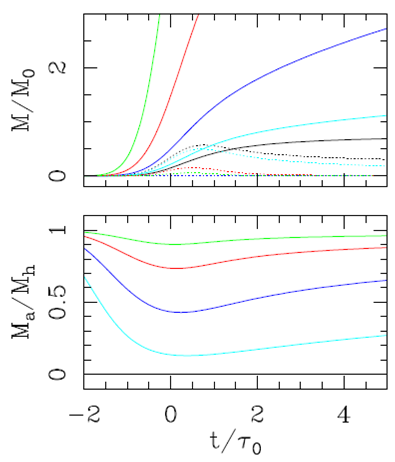
Fig. 4. Dimensionlessmass (top) of the “Gaussian density plasmon” head Mh (solid curves) and tail Mt (dashed lines), and fraction of environmental mass within the head (bottom). The results obtained for models with σ1 = 0 (black curves), 0.1 (cyan), 1.0 (blue), 10 (red) and 100 (green) are shown. The color figure can be viewed online.
6.The Velocity and Density Structure of the Tail
We now calculate the density along the plasmon tail. To this effect, we use the solution to the continuity equation of a free-streaming, plane-parallel flow:
where
where x, t and τ are related to each other through the free-streaming condition (equation 1).
In Figure 5, we show the free streaming velocity and density along the tail of the constant ejection density (see § 4) and Gaussian ejection density (§ 5) free plasmons (i.e., with σ = 0) for different evolutionary times. As shown by Raga et al. (2020, who studied a plasmon with a parabolic ejection velocity), for t > τ0 the plasmon tail develops a “Hubble law” linear velocity vs. position dependence.

Fig. 5 Velocity (top) and density (bottom) vs. position along the plasmon tails, for evolutionary times t/ τ0= 0, 1, 3, 5 and 7 (the curves are labeled with these times). The curves end in an open circle, which indicates the position (and in the top diagrams, the velocity) of the plasmon head. The results obtained for the constant ejection density case are shown in the left frames, and the ones obtained for the Gaussian ejection density on the right. The color figure can be viewed online.
For both plasmon solutions, the density along the tail has its peak value approaching the position of the plasmon head (at all times shown in Figure 5). At t = τ0, the constant ejection density plasmon tail has a second peak at x = 0, and develops a flat density vs. position structure at larger evolutionary times. At x = 0, the Gaussian ejection density plasmon has a density that → 0 at larger evolutionary times, leading to steeper density vs. position dependencies.
7.Summary
As a follow up to the paper of Raga et al. (2020), who studied the flow resulting from an ejection velocity pulse with a parabolic time-dependence (and a time-independent mass loss rate), we consider ejection pulses with different time histories.
In particular, we study the flow resulting from a collimated ejection velocity pulse with a Gaussian time-dependence, considering the cases of a constant ejection density and a density with a Gaussian time-dependence (with the same width as the ejection velocity), moving into a uniform environment. Using the “center of mass formalism” of Cantó et al. (2000), we derive full analytic solutions (given in terms of the error function) for both cases.
We calculate the position and velocity of the plasmon head as a function of time, and obtain very similar results for the constant and Gaussian ejection densities (Figure 2). The two cases produce an initial acceleration of the plasmon head, followed by a convergence to a constant velocity (for the σ = 0, “free plasmon” case) or by a gradual velocity decrease for cases with substantial environmental braking (i.e., for σ > 0).
We also calculate the mass in the head and tail of the plasmon as a function of evolutionary time. We find that:
for the constant ejection density plasmon: when σ = 0 the mass of the head is ≈ 3 times the tail mass for large evolutionary times. For , the tail has less mass, and the head much larger masses (in part, due to the accumulation of environmental material in the head).
for the Gaussian ejection density plasmon: the tail has somewhat larger masses. For times t ≈ τ0, we find that the σ = 0 solution has tail masses ≈ 2 times the head mass, but for t >> t0 this proportion is reversed.
Finally, we calculate the velocity and mass as a function of position for the σ = 0plasmons (see Figure 5). We recover the result of Raga et al. (2020) that for t > τ0 the tail has a velocity structure that approaches a linear “Hubble law” velocity vs. position. For the density structure, we see that there is a peak just before the head of the plasmon. In the rest of the tail, there are substantial differences between the constant and Gaussian ejection density cases, with the former case having zero density at x = 0, and the latter case having a density ≈ 2 times lower than the peak density (at the position just before the head).
Therefore, we find that the assumption of a constant or a Gaussian time-dependent ejection density does not affect the dynamical characteristics of the “head/tail plasmon” in a substantial way. The main differences between these two cases are the mass and the density distribution within the plasmon tail.
We should note that the dynamical characteristics of the plasmons studied in this paper are also very similar to the ones of the “parabolic velocity pulse” plasmon studied by Raga et al. (2020). From this, we conclude that at least at large evolutionary times (i.e., for t > τ0) the dynamics of the head/tail plasmon are mostly independent of the details of the velocity and density ejection histories. The only important effect of different forms of the ejection is to change the mass content and density stratification of the material in the plasmon tail.
Now, the way forward to study the head/tail plasmon flow is with full axisymmetric or 3D numerical simulations of the flow. This will allow, among other things, an evaluation of the observational characteristics of the flow and of the stability of the plasmon head at large evolutionary times. Also, it would be interesting to extend the present work to the relativistic case, since it would have clear applications to microquasars and gamma-ray bursts.











 nova página do texto(beta)
nova página do texto(beta)


