1.INTRODUCTION
The discovery of gas giant planets rotating very close to their stars (hot Jupiter, or HJs) has forced us to reconsider our model for the formation of planets around low mass stars by including in an ad hoc way large scale migration. Since this did not happen in the Solar System, it raises the natural question of understanding under what conditions large scale migration could be triggered in a proto-planetary disk (PPD). By stating such a question, we adopt the simplest view that there is only one universal process for the formation of planets, following the collapse of dense regions in a molecular cloud (McKee & Ostriker 2007; Draine 2011; Champion 2019). This reduces the problem to a more specific one, which is: how do we include migration in a well developed model like the core collapse scenario (the standard model), which explains in details how the Solar System formed (Safronov 1969; Wetherill & W. 1989; Wurm & Blumm 1996; Poppe & Blum 1997; Klahr & Brandner 2006; Hilke & Sari 2011; de Pater & Lissauer 2015; Raymond & Morbidelli 2020)
In the literature, two migration mechanisms are favored for HJs (Dawson & Johnson 2018; Raymond & Morbidelli 2020). The first is disk migration (e.g., Baruteau et al. 2014; Armitage 2020, and references therein), which proposes that a planet loses its orbit angular momentum by tidal interactions with the PPD, while the second, high-eccentricity migration (e.g., Rasio & Ford 1996; Weidenschilling & Marzari 1996; Marzari & Weidenschilling 2002; Chatterjee et al. 2008; Nagasawa et al. 2008; Beaugé & Nesvorný 2012), suggests that a planet interacting with other planets gains a higher eccentricity, which brings it close to its star where it reaches equilibrium by tidal interactions (a process know as circularization). In terms of migration, these two mechanisms might suggest that massive disks somehow amplified the level of migration compared to what happened in the Solar System, because more massive PPDs either increase the intensity of interactions of the planets with their disks or favor the formation of a higher number of planets. Within the standard model this would suggest that what counts is whether the PPD follows the minimum mass model, with a mass be- tween 0.01 to 0.02
If the initial angular momentum of the PPD passes to the planets, then one could use the orbital rotation momentum in exoplanetary systems to test different scenarios connecting the formation of the planets to the formation of their stars. For example, how is the angular momentum of the PPD coupled to the angular momentum of the stars? Since large scale migration represents a loss of angular momentum of the planets (at least by a factor 10), what was the initial angular momentum of the PPD when it formed and how does this compared to the initial mass of the PPD? Does this influence the masses of the planets and their migration? The answers are not trivial, considering that the physics involved is still not fully understood.
In particular, we know that the angular momentum is not conserved during the formation of stars. This is obvious when one compares how fast the Sun rotates with how fast its rotation should have been assuming the angular momentum of the collapsing molecular cloud where it formed was conserved. Actually, working the math (a basic problem, but quite instructive; see course notes by Alexander 2017), the Sun effective angular momentum
To explain how low-mass stars lose their angular momentum, different mechanisms are considered. The most probable one is stellar wind (Schatzman 1962; Mestel 1968), which is related to the convective envelopes of these stars. This is how low-mass stars would differ from massive ones. However, whether this mechanism is sufficient to explain the break in the J-M relation is not obvious, because it ignores the possible influence of the PPD (the formation of a PPD seems crucial; see de la Reza & Pinzón 2004). This is what the magnetic braking model takes into account (Wolff & Simon 1997; Tassoul 2000; Uzdensky et al. 2002). Being bombarded by cosmic rays and UV radiation from ambient stars, the matter in a molecular cloud is not neutral, and thus permeable to magnetic fields. This allows ambipolar diffusion (the separation of negative and positive charges) to reduce the magnetic flux, allowing the cloud to col- lapse. Consequently, a diluted field follows the matter through the accretion disk to the star forming its magnetic field (McKee & Ostriker 2007). This also implies that the accretion disk (or PPD) stays connected to the star through its magnetic field as long as it exists, that is, over a period that although brief includes the complete phase of planet formation and migration. According to the model of disk-locking, a gap opens between the star and the disk at a distance R t from the star, and matter falling between R t and the radius of corotation, R co (where the Keplerian angular rotation rate of the PPD equals that of the star), follows the magnetic field to the poles of the star creating a jet that transports the angular momentum out. In particular, this mechanism was shown to explain why the classic T-Tauris rotate more slowly than the weak T-Tauris (Ray 2012). How this magnetic coupling could influence the planets and their migrations, on the other hand, is still an open question (Matt & Pudritz 2004; Fleck 2008; Champion 2019).
To investigate further these problems, we started a new project to observe host stars of exoplanets using the 1.2 m robotic telescope TIGRE, which is installed near our department at the La Luz Observatory (in central Mexico). In paper I we ex- plained how we succeeded in determining in an effective and homogeneous manner the physical characteristics ( T eff , log g, [M/H], [Fe/H], and V sin i) of a initial sample of 46 bright stars using iSpec (Blanco-Cuaresma 2014, 2019). In this accompanying article, we now explore the possible links between the physical characteristics of these 46 stars and the physical characteristics of their planets, in order to gain new insight about a connection between the formation of stars and their planets.
2.SAMPLE OF EXOPLANETS
Our observed sample consists of 46 stars hosts of 59 exoplanets, which were selected from the revised compendium of confirmed exoplanets in the Exoplanet Orbit Database 3. In Table 1 the dominant planet (Column 2) in each stellar system is identified by the same number (Column 1) which was used in Paper I to identify their stars. In Column 3 and 4 we repeat the magnitude and distance of the host stars as they appeared in Table 1 of Paper I. This is followed by the main properties of the planets as reported in the exoplanet Orbit Database: mass (Column 5), radius (Column 6), period (Column 7), major semi-axis (Column 8) and eccentricity (Column 9). Note that an eccentricity of zero could mean the actual eccentricity is not known. The last two columns identify the detection method and the distinction between high mass and low mass exoplanet (as explained below).
TABLE 1 PHYSICAL PARAMETERS THE PLANETS IN OUR SAMPLE
| Id. # | Star and Planet | Magnitude (V) | Distance (pc) | Mp (Mjup) | Rp (Rjup) | Period (days) | ap (AU ) | ep | Detection Method | Planetary type |
| 1 | *KELT-6 c | 10.3 | 242.4 | 3.71 | 2.68 | 1276.0 | 2.39 | 0.21 | RV | HME |
| 2 | *HD 219134 h | 5.6 | 6.5 | 0.28 | 0.80 | 2198.0 | 3.06 | 0.37 | RV | LME |
| 3 | *KEPLER-37 b | 9.8 | 64.0 | 0.01 | 0.03 | 13.37 | 0.10 | 0 | Tr | LME |
| 4 | HD 46375 b | 7.8 | 29.6 | 0.23 | 1.02 | 3.02 | 0.04 | 0.05 | RV | LME |
| 5 | HD 75289 b | 6.4 | 29.1 | 0.47 | 1.03 | 3.51 | 0.05 | 0.02 | RV | LME |
| 6 | HD 88133 b | 8.0 | 73.8 | 0.30 | 1.00 | 3.42 | 0.05 | 0.08 | RV | LME |
| 7 | HD 149143 b | 7.9 | 73.4 | 1.33 | 1.05 | 4.07 | 0.05 | 0.01 | RV | HME |
| 8 | HAT-P-30 b | 10.4 | 215.3 | 0.71 | 1.34 | 2.81 | 0.04 | 0.04 | Tr | LME |
| 9 | KELT-3 b | 9.8 | 211.3 | 1.42 | 1.33 | 2.70 | 0.04 | 0 | Tr | HME |
| 10 | KEPLER-21 b | 8.3 | 108.9 | 0.02 | 0.15 | 2.79 | 0.04 | 0.02 | Tr | LME |
| 11 | KELT-2A b | 8.7 | 134.6 | 1.49 | 1.31 | 4.11 | 0.05 | 0.19 | Tr | HME |
| 12 | HD86081 b | 8.7 | 104.2 | 1.50 | 1.08 | 2.00 | 0.04 | 0.06 | RV | HME |
| 13 | WASP-74 b | 9.8 | 149.8 | 0.97 | 1.56 | 2.14 | 0.04 | 0 | Tr | LME |
| 14 | HD 149026 b | 8.1 | 76.0 | 0.36 | 0.72 | 2.88 | 0.04 | 0 | Tr | LME |
| 15 | HD 209458 b | 7.6 | 48.4 | 0.69 | 1.38 | 3.52 | 0.05 | 0.01 | Tr | LME |
| 16 | BD-10 3166 b | 10.0 | 84.6 | 0.46 | 1.03 | 3.49 | 0.05 | 0.01 | RV | LME |
| 17 | HD 189733 b | 7.6 | 19.8 | 1.14 | 1.14 | 2.22 | 0.03 | 0 | Tr | LME |
| 18 | HD 97658 b | 7.7 | 21.6 | 0.02 | 0.20 | 9.49 | 0.08 | 0.08 | Tr | LME |
| 19 | HAT-P-7 b | 10.5 | 344.5 | 1.74 | 1.43 | 2.20 | 0.04 | 0 | Tr | HME |
| 20 | KELT-7 b | 8.5 | 137.2 | 1.29 | 1.53 | 2.73 | 0.04 | 0 | Tr | HME |
| 21 | HAT-P-14 b | 10.0 | 224.1 | 2.20 | 1.20 | 4.63 | 0.06 | 0.10 | Tr | HME |
| 22 | WASP-14 b | 9.7 | 162.8 | 7.34 | 1.28 | 2.24 | 0.04 | 0.09 | Tr | HME |
| 23 | HAT-P-2 b | 8.7 | 128.2 | 8.74 | 0.95 | 5.63 | 0.07 | 0.52 | Tr | HME |
| 24 | WASP-38 b | 9.4 | 136.8 | 2.71 | 1.08 | 6.87 | 0.08 | 0.03 | Tr | HME |
| 25 | HD 118203 b | 8.1 | 92.5 | 2.14 | 1.05 | 6.13 | 0.07 | 0.29 | RV | HME |
| 26 | HD 2638 b | 9.4 | 55.0 | 0.48 | 1.04 | 3.44 | 0.04 | 0.04 | RV | LME |
| 27 | WASP-13 b | 10.4 | 229.0 | 0.49 | 1.37 | 4.35 | 0.05 | 0 | Tr | LME |
| 28 | WASP-34 b | 10.3 | 132.6 | 0.59 | 1.22 | 4.32 | 0.05 | 0.04 | Tr | LME |
| 29 | WASP-82 b | 10.1 | 277.8 | 1.24 | 1.67 | 2.71 | 0.04 | 0 | Tr | HME |
| 30 | HD 17156 b | 8.2 | 78.3 | 3.20 | 1.10 | 21.22 | 0.16 | 0.68 | Tr | HME |
| 31 | XO-3 b | 9.9 | 214.3 | 11.79 | 1.22 | 3.19 | 0.05 | 0.26 | Tr | HME |
| 32 | HD 33283 b | 8.0 | 90.1 | 0.33 | 0.99 | 18.18 | 0.17 | 0.46 | RV | LME |
| 33 | HD 217014 b | 5.5 | 15.5 | 0.47 | 1.90 | 4.23 | 0.05 | 0.01 | RV | LME |
| 34 | HD 115383 b | 5.2 | 17.5 | 4.00 | 0.96 | − | 43.5 | 0 | Im | HME |
| 35 | HAT-P-6 b | 10.5 | 277.5 | 1.06 | 1.33 | 3.85 | 0.05 | 0 | Tr | LME |
| 36 | *HD 75732 d | 6.0 | 12.6 | 3.86 | 2.74 | 4867.0 | 5.45 | 0.03 | RV | HME |
| 37 | HD 120136 b | 4.5 | 15.7 | 5.84 | 1.06 | 3.31 | 0.05 | 0.08 | RV | HME |
| 38 | WASP-76 b | 9.5 | 195.3 | 0.92 | 1.83 | 1.81 | 0.03 | 0 | Tr | LME |
| 39 | Hn-Peg b | 6.0 | 18.1 | 16.00 | 1.10 | − | 795 | 0 | Im | BD |
| 40 | WASP-8 b | 9.9 | 90.2 | 2.24 | 1.04 | 8.16 | 0.08 | 0.31 | Tr | HME |
| 41 | WASP-69 b | 9.9 | 50.0 | 0.26 | 1.06 | 3.87 | 0.05 | 0.00 | Tr | LME |
| 42 | HAT-P-34 b | 10.4 | 251.1 | 3.33 | 1.11 | 5.45 | 0.07 | 0.44 | Tr | HME |
| 43 | HAT-P-1 b | 9.9 | 159.7 | 0.53 | 1.32 | 4.47 | 0.06 | 0.00 | Tr | LME |
| 44 | WASP-94 A b | 10.1 | 212.5 | 0.45 | 1.72 | 3.95 | 0.06 | 0.00 | Tr | LME |
| 45 | WASP-111 b | 10.3 | 300.5 | 1.85 | 1.44 | 2.31 | 0.04 | 0.00 | Tr | HME |
| 46 | HAT-P-8 b | 10.4 | 212.8 | 1.34 | 1.50 | 3.08 | 0.04 | 0.00 | Tr | HME |
An * in front of the name of the planet identifies multiple planetary systems.
Among our sample, one exoplanet, # 39 (Hn- Peg b), was found to have a mass above the brown dwarf (BD) lower limit of 13 M Jup (Spiegel et al. 2011; Burgasser 2008). Note that Hn-Peg b was detected by imaging (identified as Im in Column 11), and its huge distance from its host star (Column 8) is more typical of BDs than of exoplanets (the other exoplanet detected by imaging is 34, HD 115383 b, at 43.5 AU from it stars, but with a mass of only 4 M Jup ). Another exoplanet whose mass is close to the lower mass limit for BDs is # 31 (XO-3 b), but since it is located very near its star, at 0.05 AU, there is no difficulty in accepting its classification as an exoplanet. Due to the small size of our sample, we cannot assess how the formation of exoplanets with masses above the BD limit can differ from the formation of the other exoplanets. Consequently, although we kept Hn-Peg in our sample of host stars we did not include its “exoplanet” in our statistical analysis.
Another point of importance that can be noted in Table 1 is the fact that we have only 14 exoplanets detected by RV. This is most probably due to the fact that we required the radius of the planets to be known, which is easier to determine by the Tr method. Curiously, only three of the 14 exoplanets detected by RV show the trend to be located farther from their stars than the Tr exoplanets, as observed in the literature (and as it is obvious in the Exoplanet Orbit Database). Two are close to the ice line and thus are rather warm than hot, and one with 3.86 M Jup is at the same distance as Jupiter from the Sun. This implies that any bias introduced by the different detection methods, RV vs. Tr, can- not be explored thoroughly in our present analysis.
Although the variety of the characteristics of exoplanets cannot be addressed with our present sample, we can however separate our sample of exoplanets into two groups, based on their masses. For our analysis, this distinction is important in order to test how the mass of the exoplanet is related to the mass of its host star. To use a mass limit that has a physical meaning we choose 1.2 M Jup , which is the mass above which self-gravity in a planet becomes stronger than the electromagnetic interactions (Padmanabhan 1993; Flor-Torres et al. 2016, see demonstration in Appendix A). Using this limit we separated our sample into 22 high mass exoplanets (HMEs) and 23 low mass exoplanets (LMEs). This classification is included in Table 1 in the last column.
According to Fortney et al. (2007) the mass- radius relation of exoplanets shows a trend for exoplanets above 1.0 M Jup to have a constant radius (see also Fortney et al. 2010). In fact, models of exoplanet structures (e.g., Baraffe et al. 1998, 2003, 2008) predict an inflection point in the mass-radius relation, where the radius starts to decrease instead of increasing as the mass increases. Actually, this is what we observe in brown dwarfs (BDs). Physically therefore, this inflection should be located near 1.2 M Jup , where self-gravity becomes stronger than the electromagnetic interaction and where the object starts to collapse (which is the case of BDs). However, if massive HJs have more massive envelopes of liquid metallic hydrogen (LMH) than observed in Jupiter (as suggested by JUNO; Guillot et al. 2018; Kaspi et al. 2018; Iess et al. 2018; Adriani et al. 2018), their structures might resist gravity (at least for a while), due to the liquid state being in compressible, pushing the collapse of the radius to slightly higher masses (models and observations verifying this prediction can be found in Hubbard et al. 1997; Dalladay-Simpson et al. 2016; Flor-Torres et al. 2016). This possibility, however, is still controversial, and we only use the mass limit in our analysis to separate our sample of exoplanets according to their masses. On the other hand, the possibility of massive LMH envelopes in the HMEs might have some importance, since these exoplanets would be expected to have higher magnetic fields than the LMEs , which, consequently, could affect their inter- actions with the PPD and nearby host stars (this fits the case of HD 80606 b, a HME studied by de Wit et al. 2016), leading possibly to different migration behaviors. Likewise, we might also consider the possibility of inflated radii in the LMEs, since they are so close to their stars, although less obvious is the effect of inflated radius on migration (one possibility is that they circularize more rapidly).
To test further our distinction in mass, we trace in Figure 1 the mass-radius relation of 346 exoplanets from the Exoplanet Orbit Database. Based on visual inspection it is not clear how to separate the HJs, due to inflated radii. One quantitative criterion is the mass-radius relation. In Figure 1, we traced three M -R relations, adopting 1.2 M Jup to distinguish LMEs form HMEs. Below this limit we find the relation:
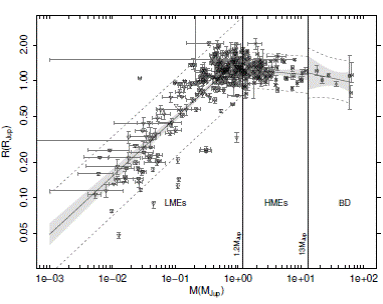
Fig. 1 The M -R diagram for exoplanets in the Exoplanet Orbit Database. The vertical line at 1.2 M Jup corresponds to the mass criterion we used to separate the exoplanets in LMEs and HMEs. The other vertical lime is the lower mass limit for the BDs, 13 M Jup .
The slope is positive and the correlation coefficient is high, r 2 = 0.75, which implies that the radius within this range of masses continually increases with the mass. This relation is also fully consistent with what was previously reported by Valencia et al. (2006) and Chen & Kipping (2017). Above the lower mass limit for BDs we find the relation:
with a negative slope and a weaker correlation coefficient of r 2 = 0.18, but sufficient to indicate that the trend is for the radius to decrease with the mass. This is as expected for objects where self-gravity is stronger than the electromagnetic repulsion (BDs not having enough mass to ignite fusion in their core cannot avoid the effect of gravitational collapse). Finally, in between these two mass limits defining the HMEs, we obtain the relation:
which has an almost nil slope and a very weak coefficient of correlation, r 2 = 0.02, consistent with no correlation. This range of mass, therefore, is fully consistent with HJs near the inflection point, extending this region over a decade in mass (as previously noted by Hatzes & Rauer 2015). For our analysis, these different M -R relations are sufficient to justify our separation between LMEs and HMEs (note that this physical criterion has never been used in the literature; the only study which uses a limit close to ours is Sousa et al. 2011).
3.CONNECTING THE STARS TO THEIR PLANETS
In Paper I, we verified that the rotational velocity of a star, V sin i, decreases with the temperature, T eff . In Figure 2, we reproduce this graphic, but this time distinguishing between stars hosting LMEs and HMEs. We observe a clear trend for the HMEs to be found around hotter and faster rotator stars than the LMEs. Considering the small number of stars in our sample, we need to check whether this result is physical or due to an observational bias. For example, one could suggest that HMEs are easier to detect than LMEs through the RV than Tr method around hotter (more massive) and faster rotator stars. To check for observational biases, we trace first in Figure 3a the distributions of the absolute V magnitude for the stars hosting LMEs and HMEs. We do find a trend for the stars hosting HMEs to be more luminous than the stars hosting LMEs. This is confirmed by a non-parametric Mann-Whitney test with a p- value of 0.0007 (Dalgaard 2008). However, in Figure 3b we also show that the reason why the stars with HMEs are more luminous is because they are located farther out, and this is independent of the detection method. Consequently, the trend for the HMEs to be found around hotter and faster rotator stars than the LMEs does not depend on the method of detection, but is a real physical difference. Considering the mass-temperature relation on the main sequence, this suggests that the more massive exoplanets in our sample rotate around more massive stars.
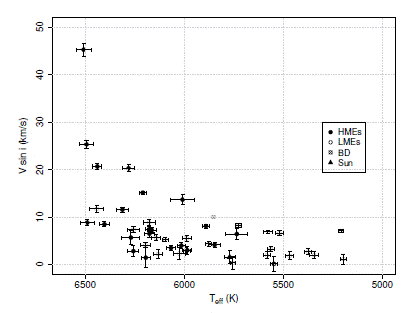
Fig. 2 Star rotational velocity vs. temperature, separating stars hosting HMEs and LMEs. The position of the Sun is included, as well as the star with a BD as companion.
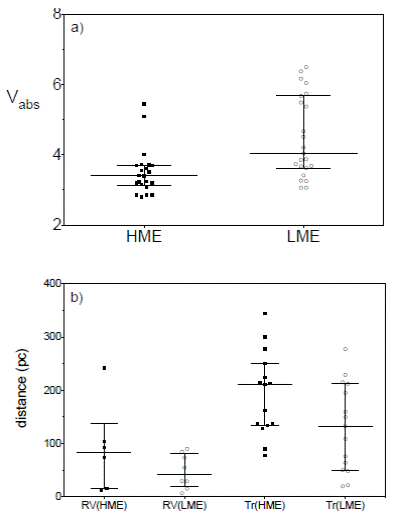
Fig. 3 a) Absolute magnitude in V separately for stars hosting HMEs and LMEs; b) Distance of the stars also separated by the detection method, radial velocity, RV, or transit, Tr. The bars correspond to the medians and interquartile ranges.
In Figure 4 we compare the physical characteristics of the stars that host HMEs with those that host LMEs. Figure 4a shows a clear trend for the rotational velocity to be higher in the stars hosting HMEs than LMEs. In Table 2 we give the results of non-parametric, Mann-Whitney (MW) tests. The use of non-parametric tests is justified by the fact that we did not find normal distributions for our data (established by running 3 different normality tests). In Column 6 we give the p-values of the tests at a level of confidence of 95%, in Column 7, the significance levels (low, *, medium, ** and high, ***) and in Column 8 the acceptance or not of the differences observed. Note that a non-parametric test compares the ranks of the data around the medians, not the means. In the case of V sin i, the MW test confirms the difference of medians at a relatively high level of confidence (stars 22, 33 and 36 were not considered due to their large uncertainties). In Figure 4b we see the same trend for T eff on average, also with a significant difference in median in Table 2.
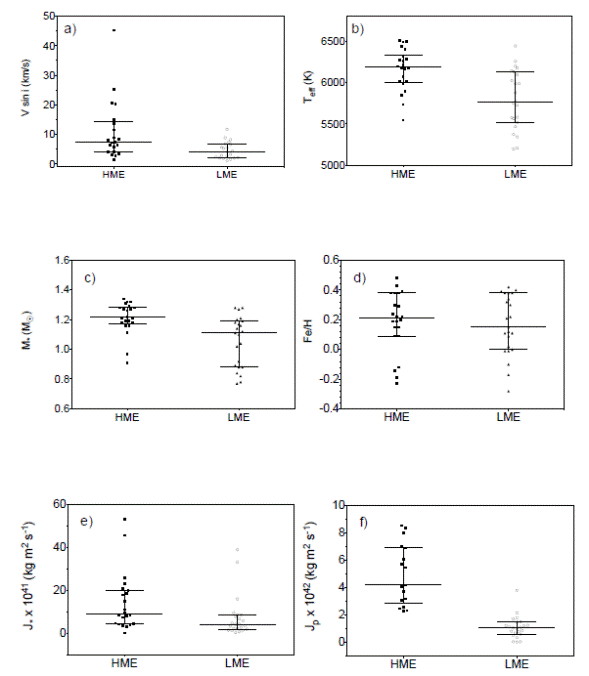
Fig. 4 Comparing the physical characteristics of the stars (and planet) hosting HMEs and LMEs. In each graph the medians and interquartile ranges are drawn over the data. a) rotational velocity, b) effective temperature, c) mass of the star, d) metallicity, e) the angular momentum of the star, f) the angular momentum of the orbit of the dominant planet.
Table 2 Statiscal tests
| HME | LME | MW | Sing. | Diff. | ||||
| Parameter | Median | Mean | Median | Mean | p-value | |||
| V sin i | 7.47 | 10.94 | 4.11 | 4.62 | 0.0048 | ** | yes | |
| Teff | 6186 | 6158 | 5771 | 5800 | < 0.0001 | *** | yes | |
| M∗ | 1.22 | 1.21 | 1.11 | 1.05 | < 0.0001 | *** | yes | |
| [Fe/H] | 0.21 | 0.19 | 0.15 | 0.16 | 0.6810 | ns | no | |
| J∗ | 8.83 | 14.3 | 4.17 | 7.33 | 0.0096 | ** | yes | |
| Jp | 4.17 | 4.93 | 1.04 | 1.09 | < 0.0001 | *** | yes | |
The units and scale values for the medians and means are those of Figure 4.
In Figure 4c the difference in mass is obvious, and confirmed by the MW test at the highest level of confidence. Stars with HMEs are more massive than stars with LMEs. On the other hand, we find no difference in the distribution of the metallicity. Although the medians and means reported in Table 2 look different, the p-value of the MW test is unequivocal, being much higher than 0.05. The median [Fe/H] for our sample is 0.07 dex and the mean is 0.12 dex, with a standard deviation of 0.24 dex. These values are comparable to those reported in the literature for systems harboring massive HJ exoplanets (Sousa et al. 2011; Buchhave et al. 2012).
In Figures 4d and 4f, once again we distinguish obvious differences in the distributions, the stars with HMEs having higher angular momentum than the stars with LMEs, and the HMEs having also higher angular momentum than the LMEs. The MW tests in Table 2 confirmed these differences at a relatively high level of confidence (like for V sin i). Considering Eq. 2 in Paper I for the angular momentum of the star, the statistical test confirms that the HMEs rotate around more massive and faster rotator stars than the LMEs. Considering the difference in angular momentum of the exoplanets, J p , this result seems to support the hypothesis that more massive planets form in more massive PPDs with higher an- gular momentum. The question is, then, how does this difference affect the migration process of the different exoplanets?
In Figure 5a, following Berget & Durrance (2010), we trace the specific angular momentum of the stars, j ∗ = J ∗ /M ∗, as a function of their masses, distinguishing between stars hosting HMEs and LMEs. The angular momenta of all the host stars in our sample fall well below the theoretical relation proposed by McNally (1965). There is a clear distinction between the LMEs and HMEs, except for the differences encountered in Figure 4 and confirmed in Table 2, and there is no evidence that the stars follow a j − M relation.
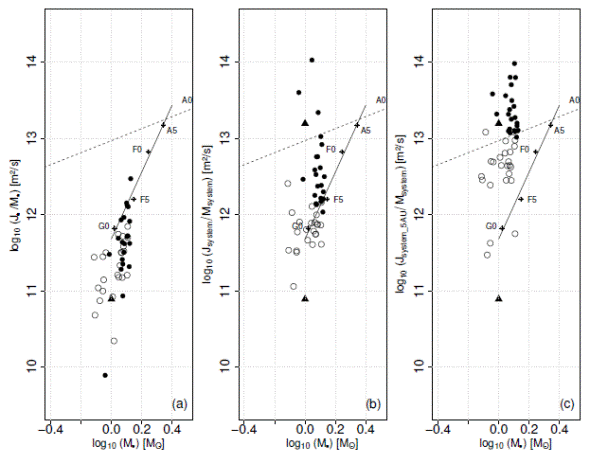
Fig. 5 In (a) Specific angular momentum of the host stars as function of their masses. The symbols are as in Figure 2. The solid black line is the relation proposed by McNally (1965) for low-mass stars (spectral types A5 to G0) and the dotted line is the extension of the relation suggested for massive stars. The black triangle represents the Sun; (b) specific angular momentum for the planetary systems, with the inverted black triangle representing the Solar system; (c) original angular momentum assuming the planets formed at 5 AU.
On the other hand, when we compare in Figure 5b the angular momentum for the systems, j sys = j ∗+j p , we do see a difference between systems with LMEs and HMEs. But this is expected since, by definition, the HMEs having higher masses naturally have a higher contribution to j sys . However, and de- spite being more massive than Jupiter, very few of the HME systems have a value of j sys comparable to the Solar System. Obviously, this is because of the large scale migration they suffered. To illustrate this point, we traced in Figure 5c the possible “initial” angular momentum the system could have had assuming the exoplanets formed at the same distance as Jupiter (5 AU). Comparing with the positions in Figure 5b, the HMEs would have lost on average 89% of their initial momentum, compared to 86% for the LMEs. Those losses are enormous. Considering the loss of angular momentum of the stars and planets, it might be difficult to expect a coupling between J p and J ∗ or even a j − M relation.
As a final test, we have calculated the Pearson correlation matrices (also explained in Dalgaard 2008) for the systems with HMEs and LMEs. The results can be found in Table 3 and Table 4. Since the correlation matrices are symmetrical we include only the lower diagonal of each, showing first the matrix with the p-values (with alpha ≈ 0.05), followed by the matrix for the Pearson correlation coefficient (keeping only the significant correlations, marked in bold in the matrix of the p-values).
TABLE 3 PEARSON CORRELATION MATRIX FOR THE HME SYSTEMS
| HME log g | Teff 0.2918 | log g | [F e/H] | V sin i | R∗ | M∗ | J∗ | Mp | Rp | ap | ep |
| [F e/H] | 0.6794 | 0.1519 | |||||||||
| V sin i | 0.0048 | 0.6052 | 0.4121 | ||||||||
| R∗ | 0.0199 | 0.0785 | 0.9143 | 0.8734 | |||||||
| M∗ | <0.0001 | 0.0884 | 0.4889 | 0.1242 | <0.0001 | ||||||
| J∗ | 0.0006 | 0.7412 | 0.1961 | <0.0001 | 0.2345 | 0.0162 | |||||
| Mp | 0.8087 | 0.7356 | 0.3401 | 0.3785 | 0.0577 | 0.1892 | 0.7779 | ||||
| Rp | 0.3861 | 0.4608 | 0.2527 | 0.9065 | 0.2122 | 0.1460 | 0.8397 | 0.1323 | |||
| ap | 0.0339 | 0.0173 | 0.6018 | 0.9447 | 0.0118 | 0.0074 | 0.3824 | 0.0074 | 0.1050 | ||
| ep | 0.6455 | 0.4758 | 0.8288 | 0.9864 | 0.4266 | 0.1871 | 0.8931 | 0.0073 | 0.0418 | 0.0122 | |
| Jp | 0.4358 | 0.4193 | 0.4496 | 0.5536 | 0.0455 | 0.5697 | 0.7913 | <0.0001 | 0.2679 | <0.0001 | 0.0234 |
| log g | |||||||||||
| [F e/H] | |||||||||||
| V sin i | 0.5909 | ||||||||||
| R∗ | 0.4925 | ||||||||||
| M∗ | 0.8402 | 0.8662 | |||||||||
| J∗ Mp | 0.6736 | 0.9857 | 0.5064 | ||||||||
| Rp | |||||||||||
| ap | -0.4539 | 0.5021 | -0.5267 | -0.5546 | 0.5544 | ||||||
| ep | 0.5550 | -0.4373 | 0.5243 | ||||||||
| Jp | -0.4305 | 0.9393 | 0.7272 | 0.4811 |
TABLE 4 PEARSON CORRELATION MATRIX FOR THE LME SYSTEMS
| LME log g | Teff 0.0002 | log g | [F e/H] | V sin i | R∗ | M∗ | J∗ | Mp | Rp | ap | ep |
| [F e/H] | 0.3461 | 0.2153 | |||||||||
| V sin i | 0.0097 | 0.0389 | 0.0761 | ||||||||
| R∗ | <0.0001 | <0.0001 | 0.2374 | 0.1499 | |||||||
| M∗ | <0.0001 | <0.0001 | 0.0618 | 0.0187 | <0.0001 | ||||||
| J∗ | 0.0034 | 0.0012 | 0.1880 | <0.0001 | 0.0077 | 0.0012 | |||||
| Mp | 0.0658 | 0.1672 | 0.5022 | 0.3259 | 0.3008 | 0.1802 | 0.3683 | ||||
| Rp | 0.1825 | 0.0681 | 0.5140 | 0.7583 | 0.1878 | 0.1902 | 0.9893 | <0.0001 | |||
| ap | 0.4458 | 0.5652 | 0.5036 | 0.9258 | 0.4294 | 0.4570 | 0.8521 | 0.0303 | 0.2162 | ||
| ep | 0.2682 | 0.3735 | 0.3691 | 0.2266 | 0.5929 | 0.3681 | 0.3979 | 0.0645 | 0.0348 | 0.2426 | |
| Jp | 0.2301 | 0.1979 | 0.7299 | 0.2168 | 0.4060 | 0.3170 | 0.1022 | <0.0001 | 0.0029 | 0.7167 | 0.4335 |
| log g | -0.6992 | ||||||||||
| [F e/H] | |||||||||||
| V sin i | 0.5506 | -0.4537 | |||||||||
| R∗ | 0.7509 | -0.9084 | |||||||||
| M∗ | 0.9036 | -0.8577 | 0.5081 | 0.9407 | |||||||
| J∗ Mp | 0.5840 | -0.6319 | 0.9312 | 0.5408 | 0.6327 | ||||||
| Rp | 0.7468 | ||||||||||
| ap | -0.4521 | ||||||||||
| ep | -0.4418 | ||||||||||
| Jp | 0.67921 | 0.5927 |
Comparing the HMEs with LMEs, there are obvious correlations of the temperature with the mass and radius in both systems, which suggests that, in general, as the temperature increases, the mass and radius increase. This explains, therefore, the strong correlations in both systems of the temperature with the velocity of rotation and thus the angular momentum. Note that these results are consistent with the general relation we determined in Paper I between V sin i, T eff and log g. This suggests that the more massive the star the faster its rotation.
One difference between the two systems is that, although there are no correlations of the temperature with the surface gravity in the HMEs, there is an anticorrelation in the LMEs. Due to the smallness of our samples, it is difficult to make sense of this difference physically. However, we note that log g in the LMEs is also well correlated with the radius, the mass and the angular momentum (but not V sin i it- self), something not seen in the HMEs. In Figure 2 wee see that the dispersion of V sin i decreases at low temperatures, which implies that the bi-exponential relation of V sin i as a function of T eff and log g be- comes tighter, suggesting that the behavior of log g becomes more ordered, which could explain the anticorrelations with T eff and the correlations with M ∗ and R ∗ (and thus also with J ∗).
It is remarkable that [Fe/H] in both systems is not correlated with any of the other parameters, either related to the stars or the planets. For the stars, the most obvious correlations in both systems are between M ∗ and R ∗, or V sin i and J ∗. Note also that although V sin i shows no correlation with M ∗ and R ∗ in the HMEs it is correlated with M ∗ in the LMEs. This might also explain why R ∗ is not correlated with J ∗ in the HMEs, while it is in the LMEs.
In the case of the planets, the most important result of this analysis is the (almost complete) absence of correlations between the parameters of the planets and the parameters of the stars (most obvious in the LMEs). The only parameter that shows some correlation with the star parameters is the semi-axis, a p , of the orbit of the planets in the HMEs. This might suggests a difference in terms of circularization. Two results also seem important. The first is that R p is only correlated to M p in in the HMEs, which is consistent with the fact that the radius of the HMEs is constant. The second is that there is no correlation between J p and J ∗, which is consistent with the behavior observed in Figure 5, and which could suggest that there is no dynamical coupling between the two. This, probably, is due to important losses of angular momentum during the formation of the stars and to migrations of the planets.
4.DISCUSSION
Although our sample is small, we do find a connection between the exoplanets and their stars: massive exoplanets tend to form around more massive stars, these stars being hotter (thus brighter) and rotating faster than less massive stars. When we compare the spin of the stars with the angular momentum of the orbits of the exoplanets, we find that in the HME systems both the stars and planets rotate faster than in the LME systems. This is consistent with the idea that massive stars formed more massive PPDs, which rotate faster, explaining why the planets forming in these PPDs are found also to rotate faster.
When we compare the effective angular momenta of the stars (Figure 5a) we find no evidence that they follow a j M relation, in particular, like the one suggested by McNally (1965), or that the angular momentum of the systems (Figure 5b) follows such relation. Furthermore, there is a correlation between J p and J ∗, which suggests that there is no dynamical coupling between the two. This is probably due to the important losses of angular momentum of the stars during their formation (by a factor of 106) and of the planets during their migrations (higher than 80% of their possible initial values). For the planets, their final angular momenta depend on their masses when their migration ends, a p . Assuming, consequently that they all form more or less at the same distance (farther than the ice line in their systems) and end their migration at the same distance from their stars (which seems to be the case, as we show in Figure 6), the HMEs would have lost a slightly larger amount of angular momentum than the LMEs.
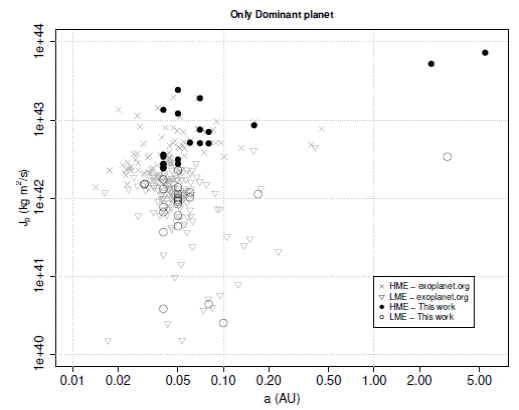
Fig. 6 Angular momentum of the exoplanets in our sample with respect to their distances from their stars. For comparison, the exoplanets in our initial sample are also shown as light gray signs.
Within the scenario suggested above, this might suggest that more massive PPDs are more efficient in dissipating the angular momentum of their planets.
One thing seems difficult to understand, however. Considering that HMEs are more massive and lost more angular momentum during their migration, why did they end their migration at almost exactly the same distance from their stars as the less massive LMEs?. In Figure 6 the accumulation we perceive between 0.04 and 0.05 AU is consistent with the well known phenomenon called the three-days pile-up (3 days is equivalent to slightly more than 0.04 AU, assuming Kepler orbits), which is supposed to be an artifact due to selection effects of ground- based transit surveys (Gaudi 2005). However, Dawson & Johnson (2018) in their review about migration suggested that this could be physical, and some authors did propose different physical explanations (see Fleck 2008, and references therein). The model of Fleck (2008) is particularly interesting because it tries to solve the problem using the same structure of the PPD that many authors believe explains how the stars lose their angular momentum during the T-Tauri phase, that is, by magnetic braking. In Appendix B we do some calculations which show that the radius where the planets in our sample end their migration could be close to the co-rotation radius, the region of the PPD where the disk rotates at the same velocity as the star. But does this imply that disk migration is more probable than high- eccentricity tidal migration?
According to the theory of high-eccentricity tidal migration, one expects a strong dependence of the tidal evolution timescale on the final location of the orbit of the planets, a final (e.g., Eggleton 1998):
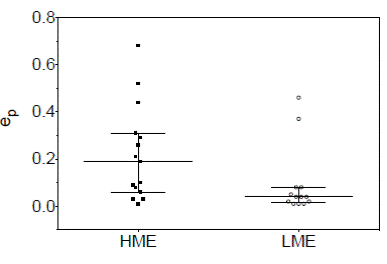
This implies that since the HMEs and LMEs have the same a final 0.04 AU they should also have the same tidal evolution timescale, and thus no difference would be expected comparing their eccentricities. What stops the planet migration in the high-eccentricity tidal migration model is the circularization of the orbit through tidal interactions with the central star. Therefore, assuming the same tidal evolution timescale, we would expect the eccentricities for the HMEs and LMEs to be all close to zero (Bolmont et al. 2011; Remus et al. 2014). Note that using our data to test whether the HMEs and LMEs have similar distributions in eccentricity is possibly difficult, because we are not certain if an eccentricity of zero is physical or not (meaning an absence of data). For the HME sample, on 22 exoplanets we count 7 (32%) with zero eccentricity, while in the LMEs out of 23, 10 (43%) have zero eccentricity. The difference seems marginal. For the remaining planets with non zero eccentricities (15 HMEs and 13 LMEs) we compare in Figure 7 their distributions. There is a weak difference, with a median (mean) of e p = 0.19 (e p = 0.22) for the HMEs compared, to e p = 0.04 (e p = 0.10) for the HMEs and LMEs. A MW test yields a p-value = 0.0257, which suggests a difference at the lowest significance level. Therefore, there seems to be a trend for the HMEs to have on average a higher eccentricity than the LMEs. The HMEs possibly reacted more slowly to circularization than the LMEs (de Wit et al. 2016), suggesting possibly different structures due to their larger masses (Flor-Torres et al. 2016).
5. CONCLUSIONS
Based on an homogeneous sample of 46 stars observed with TIGRE and analysed using iSpec we started a project to better understand the connection between the formation of the stars and their planets. Our main goal is to check whether there could be a coupling between the angular momentum of the planets and their host stars. Here are our conclusions.
There is a connection between the stars and their exoplanets, which passes by their PPDs. Massive stars rotating faster than low-mass stars had more massive PPDs with higher angular momentum, explaining why they formed more massive planets rotating faster around their stars. However, in terms of stellar spins and planet orbit angular momentum, we find that both the stars and their planets have lost a huge amount of angular momentum (by more than 80% in the case of the planets), a phenomenon which could have possibly erased any correlations expected between the two. The fact that all the planets in our sample stop their migration at the same distance from their stars, irrespective of their masses, might favor the views that the process of migration is due to the interactions of the planets with their PPDs, and that massive PPDs dissipate more angular momentum than lower mass PPDs. Consistent with this last conclusion, HMEs might have different structures than LMEs, which made them more resilient to circularization.











 nova página do texto(beta)
nova página do texto(beta)