1.INTRODUCTION
The suggestion that the knotty structures in astrophysical jets could be the result of a time-dependent ejection was first made in the context of extragalactic jets (see, e.g., Rees 1978; Wilson 1984; Roberts 1986). However, the theory of variable jets has been mostly developed and applied in the context of Herbig-Haro (HH) jets from young stars.
Raga et al. (1990) apparently first pointed out in an explicit way that the structures observed in HH jets could be easily modeled as “internal working surfaces” produced by an ejection velocity variability with a hypersonic amplitude (though the general idea that HH knots are the result of a variability of the ejection hovers around in the literature of the late 1980’s). Since then, a relatively large number of papers has been written on numerical simulations and analytic models of variable ejection HH jets, as well as comparisons with observations (three relatively recent examples are Teşileanu et al. 2014; Hansen et al. 2017; Castellanos-Ramirez et al. 2018).
Kofman & Raga (1992) and Raga & Kofman (1992) studied analytically the asymptotic regime reached by internal working surfaces at large distances from the outflow source. They noted that the internal working surface shocks (see Figure 1) asymptotically have shock velocities that scale as 1/x and pre-shock densities with the same dependence on distance x from the source. Approximating the emission from these shocks with the predictions from plane-parallel shocks, Raga & Kofman (1992) showed that the asymptotic working surface model predicts a [S II] line intensity vs. x decay that agrees surprisingly well with observations of the HH 34 jet. More recently, Raga et al. (2017) showed that the successive knots along the HH 1 jet have the predicted [S II] intensity vs. position dependence, and also that individual knots follow the predicted behaviour as a function of time, following the increase in x that results from their motion away from the outflow source.
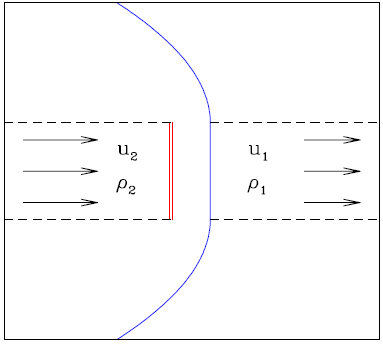
Fig. 1 Schematic diagram of an internal working surface produced by the interaction of slower material (of velocity u1 and density ρ 1) with faster material (of velocity u 2 and density ρ 2) ejected at later times. The working surface has two shocks. the bow shock (blue, solid line) and the “jet shock” (double, solid red line). The dashed lines represent the outer boundary of the jet beam. The color figure can be viewed online.
Kofman & Raga (1992) and Raga & Kofman (1992) found the asymptotic regime by considering a “ram-pressure balance” equation of motion for the internal working surfaces. This equation of motion is valid for the case in which the gas that goes through the working surface shocks is ejected laterally in an efficient way, and does not remain within the working surface. Though these authors determined the form of the position dependence of the shock velocities and pre-shock densities of the internal working surfaces, they were unable to relate the proportionality constants of these dependencies to the functional form of the ejection velocity and density.
In this paper, we study the asymptotic regime (of internal working surfaces at large distances from the outflow source) using the “center of mass” equation of motion of Cantó et al. (2000). This equation of motion is valid for internal working surfaces in which a large part of the gas passing through the shocks stays within the working surface. The theoretical attraction of this formalism is that it generally leads to full (though possibly quite complex) analytic solutions (see, e.g., Cantó & Raga 2003).
The paper is organized as follows. In § 2 we provide a summary of the “center of mass formalism” of Cantó et al. (2000), giving the equation of motion for the internal working surfaces and the free-flow (velocity and density) solution for the continuous jet beam segments between the working surfaces. In § 3, we derive the full asymptotic solution for large distances from the outflow source. In § 4, we derive the properties of the working surfaces for a limited set of chosen ejection velocity and density variabilities. In § 5, we calculate the Hα and red [S II] position- dependent luminosities of the asymptotic working surfaces. In § 6, we discuss the “inverse problem” of taking the observed properties of a knot (in particular, the spatial velocity and line luminosity of a given knot, and the knot position and knot spacing) and deducing the mean mass loss rate of the out- flow. In § 7, we use this inverse problem to deduce the mass loss rate of the HH 1 jet. Finally, the results are summarized in § 8.
2.Equation of motion for an internal working surface
This section is a short summary of the “center of mass equation of motion” for working surfaces derived by Cantó et al. (2000). The idea embodied by this formalism is as follows:
in a hypersonic jet (or wind), in the absence of shocks the fluid parcels are free-streaming, preserving their initial ejection velocity u 0,
when shocks form due to “catching up” of faster parcels ejected at later times with slower parcels ejected at earlier times, “internal working sur- faces” are formed (see Figure 1). These working surfaces are assumed to be compact (with ex- tents along the outflow direction which can be neglected), so that each of them has a single, time-dependent distance from the source x ws ,
if one assumes that all of the mass entering through the two working surface shocks stays in a region close to the working surface (an assumption that is correct for a spherical wind, and might also be appropriate for radiative jets), then:
with this “mass conservation” condition, a working surface can be seen as a particle formed by the coalescence of fluid parcels, with the mass and momentum of the coalesced parcels. Then, the position x ws of the working surface will be equal to the position x cm of the center of mass of the fluid parcels if they had continued free- streaming without coalescing.
Cantó et al. (2000) showed that this center of mass can be calculated as a function of the ejection velocity and density history in a direct way, leading to analytic solutions for the time-dependent positions and velocities of the successive internal working surfaces. Here, we summarize their results.
Let us assume an arbitrary, periodic variation u0(τ), p0(τ) of the ejection velocity and density. This periodic ejection variability produces a chain of internal working surfaces, and we consider the time- dependent position
of the centre of mass of the material within one of the working surfaces. In this equation, t is the present time, and τ ≤ t is the “ejection time” at which the fluid parcels were ejected. The position x(t, τ ) of the free-streaming fluid parcels is given by the free- streaming flow condition
The τ 1 and τ 2 values in equation (1) are the ejection times of the fluid parcels which are now entering the working surface from the downstream and upstream directions (respectively), and correspond to two successive roots of the equation:
We also note that the density of a free-streaming jet with a position-dependent cross section σ(x) is given by:
where σ0 and p0(τ) are the ejection cross section and density, respectively, and
3.The asymptotic regime
For large distances from the source, most of the ejected material has already entered the working surfaces, so that the ejection time-interval of the material entering the working surface from the upstream and downstream directions becomes τ 2 − τ 1 ≈ τ p , where τ p is the period of the ejection variability. In this regime, the τ 1 → τ 2 interval of the integrals can therefore be replaced by the τ p /2 τ p /2 interval. Equation (1) then becomes:
where
is the (constant) asymptotic velocity of the working surface and
is an average ejection time of the material that lies within a given internal working surface. Clearly, by choosing to carry out the integrals over the τ p /2τ p /2 ange we are choosing the internal working surface formed by the material ejected in this ejection time interval.
Therefore, regardless of the form of the periodic ejection velocity and density variability, at large distances from the source the working surfaces travel at a constant velocity, which is given by equation (6). It is also possible to obtain the shock velocities of the working surface shocks in the following way.
At large distances from the source, the material in the continuous segments of the jet corresponds to a small range of ejection times around τ n , where the index n numbers the successive continuous segments. The ejection time τ n is determined by the condition
where one has to choose the root with
and the free-streaming flows on the two sides of the working surface have linear velocity vs. position relationships, giving velocities
immediately down- and up-stream of the working surface.
Using equation (9), we have
With ∈ <<1 in the asymptotic regime.
We can then use equations (5), (10) and (11) to calculate the velocity jump accross the working surface:
where we have carried out a first order expansion in ϵ (see equation 11).
Also, the free-streaming flow density integral (4), when evaluated in τ n gives:
where we can calculate both upstream and down- stream densities using τ n , given that in the asymptotic regime we have ϵ << 1 (see equation 11). In this equation, σ 0 is the ejection cross section and σ(x cm ) the cross section at the position of the working surface. Equation (13) can be further simplified by noting that
and therefore, in the asymptotic, ϵ << 1 regime the first term in the denominator of equation (13) can be neglected. In this way, we obtain
with equal densities on both sides of the internal working surface. The fact that the densities on both sides of the working surface asymptotically approach each other, and that the velocity of the working sur- face becomes constant, implies that the shock velocities of the two working surface shocks also have the same value. Therefore, the velocity jump ∆u across the working surface (see equation 12) is divided into two shocks of velocities ∆u/2. In this way, we see that as the working surface travels away from the outflow source at the asymptotic velocity v a , the shocks have velocities that decrease as 1/x cm (see equation 12).
Combining equations (5), (15) and (8) we obtain:
Where
is a (positive) constant, σ(x cm ) is the cross section of the jet (at the position of the working surface) and ρ 0 and u˙0 are calculated at the time τ n at which the material of the asymptotic segments of continuous jet beam were ejected, which is given by equation (8).
4.Examples for a sinusoidal U 0 (τ ) and two simple forms of ρ 0 (τ )
4.1.Ejection Velocity Variability
For the ejection velocity, we choose a sinusoidal variability:
with mean velocity u 0, half-amplitude Δu 0, frequency ω and period τ p = 2 π / ω. The half amplitude Δu 0 lies in the 0 → u 0 interval.
4.2.Constant M˙
We first choose a density variability such that the jet has a time-independent M˙ . The ejection density then is:
where σ 0 is the ejection cross section, and where we have used equation (18) for the second equality.
With the chosen u 0(τ ) and ρ 0(τ) (equations 18 and 19, respectively), from equation (6) we obtain
from equation (8) we obtain
and from equation (17) we obtain
In this way, we can calculate the shock velocities ∆u/2 (see equation 12) and pre-shock densities ρ
1 = ρ
2 (see equation 16) of the asymptotic working surfaces as a function of their position x
cm
, the jet cross-section σ(x
cm
), the (time-independent) mass loss rate
4.3.Constant ρ 0
We now consider the case of a time-independent ejection density ρ
0. Then, the time-averaged mass loss rate of the ejected jet is
Using equation (18) and setting a time- independent ρ 0, from equation (6) we obtain
from equation (8) we obtain
and from equation (17) we obtain
With
If we consider the ∆v 0 /v 00 lower limit of the velocity amplitude, we regain the results obtained for the constant mass loss rate case (see § 4.2). If we consider the ∆v 0 /v 0 → 1 upper limit, we obtain:
And
Therefore, in the ∆v
0
/v
0
→ 1 large amplitude limit the constant ρ
0 case gives an asymptotic velocity v
a
for the working surfaces which is a factor 3/2 larger than the one of the constant mass loss case, and a “density constant” Σ larger by a factor
5.The emission of asymptotic working surfaces
We now estimate the Hα and red [S II] luminosities of the asymptotic working surfaces as:
where σ is the cross section of the jet at the position of the working surface, n pre = ρ 1,2 /(1.3m H ) (where ρ 1,2 is the pre-working surface shock density, see equation 16), v s = ∆u/2 is the shock velocity (see equation 12), and I line is the line flux emerging from one of the two shocks (the factor 8π accounting for the fact that we have 2 shocks radiating into 4π sterad).
As described in Appendix A, we use the plane- parallel, steady shock models of Hartigan et al. (1987) to determine the functional form:
with f line = f Hα or f [SII] determined from fits to the predictions of the plane-parallel shock models (see equations A38 and A39 of Appendix A).
Combining equations (30), (31), (16) and (25), we obtain:
Where
For a sinusoidal ejection velocity variability and a density variability such that the mass loss rate is time-independent (see § 4.2), the position-dependent luminosity of the working surface in the Hα and [S II] lines can be obtained by setting f = f Hα (see equations A38 and A39 in Appendix A, respectively) and g(∆v 0 /v 0) = 1 (see equation 22).
For the case of a constant density ejection, the Hα and [S II] luminosities can be obtained using the g(∆v 0 /v 0) function of equation (26). For ∆v 0 /v 0 << 1, this function has a value g(∆v 0 /v 0) ≈ 1.
6.The inverse problem
Several HH outflow systems show chains of quasi- periodic, aligned knots within ≈1017 cm (≈104 AU) of the outflow source. These knots generally have spatial velocities in excess of ≈150 km s−1 (deter- mined from radial velocity and proper motion studies), and have very low excitation emission line spectrum, with high red [S II]/Hα and [O I] 6300/Hα line ratios. These line ratios imply relatively slow shock velocities (of ≈ 20-30 km s−1).
In the case of the HH 1 jet, this very low excitation is present in all of the observed knots along the HH 1 jet, including the knots that lie closer to the outflow source (observed in the IR, see, e.g., Table 2 of Nisini et al. 2005). The knots formed by a velocity variability with a half-amplitude ∆v 0 produce internal working surfaces that rapidly reach peak shock velocities v s ≈ ∆v 0 (before reaching the asymptotic regime described in § 3), as shown, e.g., by Raga & Cantó (1998) and Cantó et al. (2000). There- fore, the low excitation of all knots along the HH 1 jet (and in particular, the ones closer to the outflow source) indicates that the ejection time variability in HH 34 has a small ∆v 0 /v 0 (where v 0 is the mean ejection velocity, and ∆v 0 is the half-amplitude of the variability, see, e.g., equation 18). A similar situation is found for the HH 1 jet, and for other jets in which all of the knots along the chains close to the outflow source have a very low excitation spectrum (e.g., HH 34, see Podio et al. 2006.
In this section we show how observational determinations of the knot spacing ∆x, and the luminosity L line of a given emission line and spatial velocity v a of a knot at position x ws can be used to constrain the average mass loss rate of the ejection. We will identify the observed position x ws of the knot with the x cm center of mass position that comes out of our model, so that in the following we will set x cm = x ws .
For a low-amplitude sinusoidal ejection velocity variability, both the constant mass loss rate and constant ejection density cases (see § 4.2 and § 4.3) give:
where v a is the asymptotic working surface velocity, and x ws is the position of a given working surface. The line emission of the working surface is then given by equation (32) with g(∆v 0 /v 0) = 1.
For a periodic ejection velocity, all of the working surfaces in the asymptotic regime move with the constant velocity v a . Therefore, if we observe the spatial velocity v a (determined from proper motion and radial velocity measurements) and knot spacing ∆x, we can obtain the variability period as
We now observe the flux of a given emission line, and using the distance to the object and the extinction (which we assume has also been determined) we can calculate the luminosity Lline of the line. If the observed knot lies at a distance xws from the outow source, we first use equation (12) to calculate the shock velocity of the two working surface shocks:
With our empirical determinations of Lline, τ p and vs, we then invert equation (32) (setting g = 1, see above) to calculate the average mass loss rate
where in Appendix A we give analytic forms for the f line (v s ) functions for the Hα and red [S II] emission. Clearly, in order to calculate the mass loss rate, we need to know the value of the half-amplitude ∆v 0 of the ejection velocity variability. If we cannot deter- mine this parameter from other observations, we can set ∆v 0 ≈ v s .
7.An application to the HH 1 jet
As an example we consider the “HH 1 jet”, which points from near the source of the HH 1/2 out- flow system towards HH 1. Raga et al. (2017) and Castellanos-Ramirez et al. (2018) argue that the intensity vs. position dependence of the knots at distances > 5´´′ from the source can be modelled as coming from working surfaces in the “asymptotic regime”.
We calculate the mass loss rate of the HH 1 jet using the calibrated line fluxes of knot G by Nisini et al. (2005). At the time of their observations, the G knot was at x G = 6.5´´′ = 3.9 x 1016 cm from the out- flow source. From the HST images shown in Raga et al. (2017), we see that the separation between successive knots is ∆x G ≈2´´′ = 1.2x 1016 cm. Also, the proper motion velocity of knot G is v G = 287 km s−1, which is very close to its full spatial velocity because the outflow lies at a very small angle with respect to the plane of the sky.
First, with the x G , ∆x G and v G values, we use equations (34) and (35) to obtain a period τ p = 13.3 yr and a shock velocity v s = 44.2 km s−1.
Then, taking the knot G line fluxes from Nisini et al. (2005), applying a reddening correction with their A
v
= 2.0 extinction (taking a standard, E(B − V )/A
v
= 3.1 extinction curve) and assuming a distance of 400 pc to HH 1, we obtain L
Hα
= 1.77 × 10−4
These two mass loss rate estimates can be com- pared with the estimates of Nisini et al. (2005). who (using different methods) find
8.SUMMARY
We have applied the “center of mass equation of motion” to find the asymptotic behaviour (at large distances from the outflow source) of the internal working surfaces produced by an arbitrary, periodic out- flow variability with an ejection velocity u 0(τ ) and a density ρ 0(τ). We find the complete asymptotic solution, giving the constant, asymptotic velocity v a and the position-dependent shock velocities and pre- shock densities of the working surfaces.
We obtain the same position-dependencies that have been found by Raga & Kofman (1992) using the “ram-presure balance” equation of motion for the working surfaces. However, Raga & Kofman (1992) were unable to find the relation between the proportionality constants (for the density and shock velocity vs. position) and the ejection variability.
With our full asymptotic solution, we compute the knot properties for two chosen combinations of u
0(τ ) and ρ
0(τ) (see § 4). We also discuss the “in- verse problem” of finding the properties of the ejection from the observational characteristics of the jet knots (see § 5). In particular, we derive a very simple expression for estimating the time-averaged mass the [S II] luminosity (i.e.,
We apply this “inverse problem” to observations of the HH 1 jet (line intensities and extinctions of Nisini et al. 2005 and proper motions of Raga et al. 2017), and find mass loss rates which are similar to the ones of Nisini et al. (2005). This result is nothing short of surprising, given the fact that our mass loss rate determination is completely model-dependent, and comes from a rather eclectic collection of observational characteristics (e.g., including the knot spacing).
This success of obtaining the previously deter- mined mass loss rate is interesting in two different ways:
it shows in a quite definite way that the interpretation of the chain of knots of the HH 1 jet as internal working surfaces formed by a quasi- periodic outflow variablity is apparently correct,
it gives us a new method for determing mass loss rates of outflows from young stars, using the spatial velocity, knot spacings and the intensity in a single emission line of the knots along the HH jet.
Less optimistically, we note that we have deter- mined (through the use of the asymptotic working surface model) the mass loss rate of the HH 1 jet from the Hα and [S II] luminosities, obtaining
In our “asymptotic working surface model” mass loss rate determinations, the obvious possible reason for the discrepancy between the Hα and [S II] results is the modelling of the emission with steady, plane- parallel shock models. As has been already noted in the early literature on modelling HH objects (see Dopita et al. 1982), the cool tail of the recombination region does not have time to develop fully in HH shock waves. The resulting “truncation” of the cooling region has a stronger effect on the predicted Hα emission than on the forbidden lines (Raga & Binette 1991), so that the mass loss rate deduced from the [S II] luminosity (i.e.,
Also, not only the shocks in working surfaces have non-steady state recombination regions, but also they are not likely to be plane. This is seen in numerical simulations of variable jets (see, e.g., Raga et al. 2007) as well as in high angular resolution observations of HH jets (see, e.g., Reipurth et al. 2002). It is therefore to be expected that analyses with the assumption of the emission being produced by plane, steady, shocks will not give fully consistent mass loss rate determinations using different emission lines.
We end by noting that there is a lot of indirect evidence that the knot structures along HH jets are the result of a variable ejection. This evidence is provided by the surprising success of variable jet models at reproducing the observed morphologies, the proper motions and the time-evolution of HH jets (see, e.g., Castellanos-Ramirez et al. 2018). However, convincing observations of a variable ejection from the outflow sources (i,e., in the spectra of the young stars or the protostars ejecting the HH jets) that can be directly linked to structures along the jets have been elusive. Some observations of the so-called “HH microjets” (with distance scales of 1016 cm and timescales of a few years) might be showing such a connection (see, e.g., Agra-Amboage et al. 2011). However, for obvious reasons such observations have not been made for the larger scale “normal” HH jets (with distance scales ≈ 1017 cm and timescales from several decades to ≈ 1000 yr).
Because of this general lack of direct link to the time-dependence of the outflow source, the details of the ejection variability cannot be determined directly and have to be chosen in a way that results in the production of a jet with the observed characteristics. In particular, while the mean velocity and characteristic period of the variability producing a chain of knots can be satisfactorily constrained by observations of the spatial motion (radial velocities+proper motions) and knot spacing, estimates of the amplitude of the ejection velocity variability depend on less convincing arguments about the ex- citation of the emission line spectrum of the knots closer to the outflow sources (see § 7).











 nova página do texto(beta)
nova página do texto(beta)