1.Introduction
FS Aur is a cataclysmic variable (CV) that shows a wide range of periodic light signals. It has a short orbital period of just 85.7 min (Thorstensen et al. 1996), a long photometric period of 205.5 min (Tovmassian et al. 2003) and a long spectroscopic period of 147 min (Tovmassian et al. 2007). The latter two periods are attributed to the precession of a fast rotating magnetic white dwarf and its beat with the orbital period, respectively (see Table 1 for details). All these frequencies were discussed in more detail in Chavez et al. (2012, hereafter CH2012). In that paper we showed the presence of a very long photometric period (VLPP) modulation observed in the long-term light curve, with a 2-mag amplitude and a period around 900 days. We argued that the origin of such modulation could be a third substellar-body (of 25 to 65 times MJ) that perturbs the eccentricity of the inner binary star system.
Table 1 Summary of periodicities detected in FS Aur
| Name/Acronym | Value | Source | Reference | Comments |
| Spin Period of WD (SP) | 1.m68-1.m75 | Ligh curve | Neustroev et al. 2005 | inconclusive |
| Orbital Period (OP) | 85.m79736±0.0004 | RVa core of H lines | Thorstensen et al 1996 unoublished data | Firm established |
| Long Spectr. Period (LSP) | 147m | RVb wings of Hlines | Tovmassian et al. 2003 | Beat between OP and LPP |
| Long Phot. Period (LPP) | 205.m45013±0.0006 | Light curve | Tovmassian et al. 2003 | Stable over ≈3000d |
| Previous Very Long Phot. Period | 875d±50d | Core of H lines | Chavez et al. 2012 | Based on ≈5000d coverage |
| (VLPP) | ||||
| New Very Long Phot. Period | 857d±78d | Core of H lines | This work | Based on ≈7500d coverage |
| (VLPP) |
aMeasured in the core of emission lines.
bMeasured in the extreme wings of emission lines.
This triple system hypothesis provided an explanation for the VLPP, and it also suggested a plausible answer for other observed peculiarities of FS Aur. More importantly is the fact that it offers a new possibility for detecting planets in accretion disk environments, where other methods fail.
There are other binary systems claimed to have a third object in a close orbit. LX Ser possesses an extra component of 7.5 MJ that explains a sinusoidal oscillation observed in the O - C diagram, with a period of 22.8 years (Li et al. 2016). Another example is V893 Scorpi where observed variations of the eclipse period of 10.2 years are interpreted as a light travel time effect caused by the presence of a giant planet with 9.5MJ (Bruch 2014). Finally DP Leonis (Beuermann et al. 2011), HW Vir (Lee et al. 2009), NN Ser (Beuermann et al. 2010), NY Virginis (Qian et al. 2012a), RR Caeli (Qian et al. 2012b) and KIC 5095269 (Getley et al. 2017) are part of this small group of post-CE binaries suspected to possess planets.
The purpose of this paper is to make use of 5 additional years of observations of FS Aurigae to see whether the VLPP signal reported in CH2012 is stronger or, on the contrary, is disappearing. We also want to model the hierarchical triple hypothesis in a more realistic manner by including eccentric and inclined orbits, and also a first order post-Newtonian correction (that is, a first order general relativity correction). Then, we study the effect that these complications have on the range of possible values of mass and semi-major axis that may explain the VLPP by secular perturbations on the cataclysmic variable.
This paper is organized as follows. In §2, we review observational data of in search of the very long photometric period (VLPP). In §3.1 we revisit the initial conditions used in our previous research and show more recent and accurate parameters for our system. In §3.2 we examine the scenario where the perturber moves in a circular and coplanar orbit, whose period is much shorter than the long period, and yet produces a binary eccentricity variation on the long period by secular perturbations. In §3.3 we extend this study to eccentric and inclined orbits. The range and properties of the allowed solutions are shown. In §3.4 we check if the VLPP could be explained as a consequence of the precession of the orbit due to first order general relativity corrections. In §3.5 we make an order of magnitude estimation for the mass transfer rate and the brightness of the system. In §4 we explore alternative scenarios for the explanation of the observed VLPP, with particular attention to the cyclic magnetic variation. In §5 we provide some final comments on the new results and their observational imprint on FS Aurigae’s features.
2.The Long and Permanent Photometric Behavior of FS Aur
Here, we use a data set 1.4 times larger than the one used earlier, covering more than 7,500 days of observations, obtained from the AAVSO public data base. From our analysis, we conclude that the long period is still present in the light curve and confirm the phenomenon reported in CH2012. The power spectrum of the data is displayed in Figure 1. The data set spans over 20 years and almost nine periods of ≈850 days, peaking in the periodogram at the 0.001167 day-1 frequency. The other low-frequency peak of similar strength at f = 0.0003919 day-1 is an alias related to the one year observational cycle. When taking into account a larger set of data, the estimated period is 857±78 days, and coincides well with the one previously reported (875±50 days) within the estimated error.
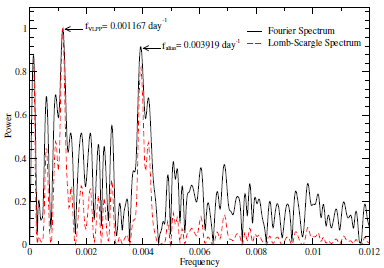
Fig 1 Normalized power spectrum of the quiescent light curve of . The solid black curve corresponds to our Fourier analysis and the red dashed curve to the Lomb-Scargle method. The strongest peak, F VLPP =0.01167 day-1 corresponds to the very long photometric period. The second highest peak frequency in the power spectrum falias = 0.03919 day-1 corresponds to an alias created by the yearly observational cycle f Y= 0.002739 day-1 and f VLPP. The color figure can be viewed online.
The upper panel of Figure 2 shows the long-term light curve for in the V band. The bottom panel of Figure 2 displays the folded light curve adjusted with a VLPP period of 857 days. The amount of data for the folded light curve was reduced averaging the magnitude per phase to be able to appreciate in detail the sinusoidal behavior. We calculated the best sinusoidal fit for the bottom panel of Figure 2, shown in red in the figure. We found that the amplitude of the best fit is ≈0.4 magnitudes, but it is also clear that the data points are disperse. Hence, we also calculated the difference between the maximum and minimum magnitude of the observed data finding 1.1 magnitude.

Fig. 2 Upper panel: long-term light curve of over the past 20 years, 1.4 times larger than in CH2012 (black filled circles correspond to new observations). Lower panel: folded light curve in quiescence using the VLPP of 857 days. We also show in red the best sinusoidal fit for this curve. The color figure can be viewed online.
3.Revisiting the Triple Cataclysmic Variable System Hypothesis
A CV is a binary system that is composed by a primary massive star (a white dwarf), and a low mass main sequence K-L type star with a predominant population of M (red dwarf) stars. They are so close to each other that the secondary star fills its Roche lobe and its surface is close to the L1 Lagrangian point.
The material that the secondary loses cannot fall directly on the primary, but instead forms a disk of material around it . This disk is so bright that outshines the brightness of both stars. In fact, its brightness is proportional to the mass transfer rate or to the mass accretion rate (Warner 1995). Therefore, if there is a change in the mass transfer rate, there will be also a change in the system’s brightness. Therefore, any change in the location of the Lagrangian L1 point will change the mass transfer and therefore the brightness of the system.
We recall that there is a huge disparity between the VLPP and all other periods. This lead CH2012 to seek a cause of the variable mass transfer rate and therefore of the disk brightness not related to the binary itself, but to propose instead a third body orbiting the binary.
The presence of a third body in the system would perturb the orbit of the stellar binary over different timescales. These timescales depend on the mass, eccentricity and semi-major axis of the unseen companion. Therefore, knowing the period of the long-term variability of the light curve of can help us place constraints on the mass and orbital configuration of the potential companion.
For this purpose, we can make use of some previously derived analytical results. In a series of papers, Georgakarakos (2002, 2003, 2004, 2006, 2009, 2015, 2016) studied the orbital evolution of hierarchical triple systems. Some of those studies involved the secular evolution of such systems. The analytical results derived there can give us an estimate about the frequency and the period of motion of the stellar binary. Therefore, we can estimate which mass values and orbital configurations of a hypothetical third companion can yield the secular period observed in the light curve of .
For a coplanar system with a perturber on a low eccentricity orbit we make use of the results of Georgakarakos (2009), while for coplanar systems with eccentric perturbers, those of Georgakarakos (2003). Finally, for systems with low eccentricity orbits and low mutual inclinations (i < 39.23o), the limit before Kozai (1962) resonances become important) we can use the relevant material of Georgakarakos (2004).
3.1.Initial Parameters
Here we discuss briefly the origin of all parameters used in this work. In CH2012 we
used the following parameters: total mass
We decided to revisit these parameters, starting with the mass and radius of the secondary. Here we use the values that appear in Knigge et al. (2011), where they use the eclipsing CVs and theoretical constrains to obtain a semi-empirical donor sequence for CVs with orbital periods Porb ≤ 6h. They give all key physical and photometric parameters of CV secondaries, as well as their spectral types, as a function of Porb.
We use the data that appear in their Tables 6 and 8 to obtain the best physical
parameters for FS Aur. We interpolate between values to find the best possible ones
for our dynamical study; they are shown in Table
2. We obtain the following mass ratio between secondary and primary
q = M2/M1 = 0.1 as shown in Table 2. The primary mass was obtained from
Knigge et al. (2011) and is based on
their previous value (Knigge et al. 2006). That value was calculated as the mean
value of the WD mass among the eclipsing CV sample available at the time
Table 2 Initial parameters of FS Aur
| Parameter | Value | References |
| Orbital period | 1.42996 hours | Thorstensen et al. (1996) |
| Orbital semi-major axis of the binary | 0.6 |
Knigge et al. (2011) |
| Secondary star mass | 0.08 |
” |
| Secondary star radius | 0.12 |
” |
| Primary star mass | 0.75 |
” |
| Primary star radius | 0.01 |
” |
| Log secondary star mass loss rate | -10.25 ( |
” |
| Secondary star temperature/spectral type | 2600/M7.0 | ” |
| Mass ratio | 0.1 | - |
We performed simulations of the CV with a hypothetical third body. In all numerical integrations, except where otherwise stated, we used the high-order Runge-Kutta-Nyström RKN 12(10) 17M integrator of Brankin et al. (1989) for the equations of motion of the full three-body problem in the barycentre inertial reference frame. In our integrations, the total energy is monitored and it is conserved up to 10-5, or better, in all experiments. At each time step, the instantaneous eccentricity of the binary is computed.
As pointed out in CH2012, tidal deformation of the stars in the close binary three-body problem can be an important effect. However, CH2012 have shown that these tidal effects are not important for this system and the two objects can be considered as point masses.
3.2.The Third Body on a Close Near-Circular and Coplanar Orbit
Hierarchical triple systems consist of two stars in a close orbit and a third body orbiting the barycentre of the close binary.
In Chavez et al. 2012 we ruled out that the VLPP could correspond directly to the period of a third body, since the object would be too far to have an important effect on the inner binary. We performed a series of numerical integrations and proved that indeed the effect is very small and could not explain the VLPP of the CV. Instead, we concluded that a third light-weight body could produce a disturbance on the central binary and that such perturbation may have a much longer period compared to the orbital period of the perturber (e.g. Mazeh & Shaham 1979, Soderhjelm 1982, Soderhjelm 1984, Georgakarakos 2002, Georgakarakos 2009). The third companion induced a long-term (secular) eccentricity modulation, as shown for example in Soderhjelm (1984).
Here, just like in CH2012, we consider a binary formed by two point masses initially in a circular orbit. A third point mass (perturber) moves initially on its own circular orbit, farther away and in the same orbital plane as the other two. Its mass M3 and orbital period P3 are varied across an ensemble of numerical experiments.
The upper panel of Figure 3 shows the log10 of the resulting periods of the long-term modulation of the binary eccentricity (vertical axis) as a function of the mass of the perturber (horizontal axis), for our ensemble of numerical experiments. Each curve corresponds to different P3/P2 ratios taken from a range of values between 12 to 48 (bottom and top curves, respectively). The thick horizontal line corresponds to the VLPP value. For example, the curve with P3/P2 = 12 does not cross the line and therefore it is a value that cannot explain the VLPP observed. For perturbers whose orbital period is smaller than 12 binary periods no solution is possible, since their respective curves do not reach the VLPP value. For perturbers with periods longer than that, but shorter than 19 binary periods, two solutions are possible: one at low mass and another at an increasingly larger mass. Finally, perturbers with periods longer than 19 produce only one solution at the large mass range.

Fig. 3 The upper panel shows the logarithm of the period of the long{term modulation of the binary eccentricity as a function of the perturber mass (Jupiter masses). Each curve corresponds to different P3=P2 ratios taken from 12.5 to 40.8; the values are 12.5, 12.7, 12.9, 13.1, 13.4, 15.6, 19, 22, 30.6, 33.6, 37.2, 40.8, from bottom to top. The thick horizontal line shows the observed value of the VLPP (857 days). Only solutions that cross this line can explain the VLPP. The middle panel shows the perturber mass and semi{major axis combinations that result in a long{term modulation of the binary orbit equal to that of the VLPP, that is, solutions that cross the black thick line. The lower panel shows the amplitude of the binary eccentricity perturbation for those solutions. See text for discussion.
The curve in the middle panel of Figure 3 shows the perturber’s orbit semi-major axis but only for the solutions that could explain the observed VLPP value; i.e solutions that cross the solid line on the upper panel. The lower panel shows the amplitude of the eccentricity perturbation for the solutions presented in the middle panel. The most efficient case would be the one in which the VLPP is the predominant effect and the eccentricity pumped into the inner binary is the largest; that is, the minimum in semi-major axis and the maximum in eccentricity. According to this study, the maximum amplitude is achieved for a system that has a third body with M3 = 29MJ and P3/P2 = 12.7.
All curves in the upper panel of Figure 3 reach a maximum value for smaller values of the mass compared to Figure 8 (upper panel) of CH2012, for the same initial conditions. Therefore, in the middle panel of Figure 3, we also obtain smaller values for the masses of the possible third body compared to the middle panel of Figure 8 of CH2012 for the same initial conditions. Then, the minimum of this curve in this research is obtained when M3 = 29MJ and P3/P2 = 12.7, while the minimum in CH2012 was obtained when M3 = 48MJ and P3/P2 =13.4.
The relative eccentricity amplitudes of these three modulations (inner binary period, third body period and secular VLPP) depend on the mass and size of the orbit of the perturber. The VLPP modulation becomes the predominant effect in the range of masses for a third body of 20MJ < M3 < 45MJ. The envelope of the calculated long-term modulation of the binary eccentricity for our best case is remarkably similar to the waveform of the VLPP.
3.3.The Third Body on an Eccentric and Inclined Orbit
Now we investigate the effect of the eccentricity and inclination of the third body on the outcome of the VLPP.
Figure 4 contains two plots for various dynamical scenarios. It is clear that there is a variety of combinations of masses and semi-major axes of the hypothetical companion that can produce the observed long term variation in the light curve of FS Aur. The perturber’s eccentricity does not seem to affect very much, as seen when we compare the two analytical solutions for e3 =0.2 and e3 = 0.5. The low e 3 solution seems to be somewhat different in the range M3/MJ = 30 - 50. Similarly, there is some difference among the solutions as the mutual inclination increases.

Fig. 4 Perturber mass and semi-major axis combinations that result in a long-term modulation of the binary orbit equal to the VLPP of 857 days. These results were obtained using the analytical formulas described in the text. In the top plot we explore the effect of the eccentricity of the third body; the inclination for all systems remains constant, i = 0o. The bottom plot explores the effect of the orbital inclination; the initial eccentricities for all systems are e3 = 0. See text for discussion. The color figure can be viewed online.
The orbital solutions based on our analytical estimates yield a wide range of
masses for our hypothetical companion, from sub-Jupiter mass bodies to big brown
dwarfs. However, all solutions may not be dynamically stable. According to the
empirical criterion developed by Holman and
Wiegert (1999), the smallest stable semi-major axis for our unseen
companion is 0.0055 AU. This value is valid for small values of e3 as
the criterion was based on simulations of massless particles initially on
circular orbits around the binary star. For initially eccentric orbits around
the stellar binary the value of the stable semi-major axis may be different. The
same holds when the companion has a mass comparable to the secondary;
3.4.Effect of a Post-Newtonian Correction
Here we consider the possible dynamical effects that a first order post-Newtonian correction to the binary’s orbit may produce on the long-term signal we observe in the light curve of the binary. We refer to the first order general relativity correction in the precessional rate of the longitude of the pericentre.
For the binary under investigation, although its total mass is under one solar mass, the small semi-major axis of its orbit makes it interesting to consider a post-Newtonian correction. Including this effect results in the precession of the pericentre at the following rate (Georgakarakos, & Eggl 2015, Naoz et al. 2015):
where G is the gravitational constant and c is the speed of light in vacuum.
Based on the precession rate given by the above equation, the period of the pericentre circulation for our system is 6812 days (18.65 yrs). Since this number is much larger than the 857 day signal we observe in the light curve of the system, we conclude that general relativity (GR) by itself cannot explain the signal.
3.5.Estimation of the Effect of the Third Body on the Mass Transfer Rate and Brightness of the System
Now that we have established that a third body can explain the VLPP observed, we estimate how the modulation of the inner binary due to the secular perturbation of the third body affects the mass transfer and hence the brightness of the system.
From the results of our numerical integrations for the third body on a close
near-circular and coplanar orbit, the most efficient solution is used for all
calculations in this subsection; that is M3 =
29MJ,P3/P2= 12.7, P3 = 18.16h.
In order to estimate the mass loss of the secondary we make use of the concept
of RL(2). Since calculating the volume of the Roche lobe is difficult, we can
define an equivalent radius of the Roche Lobe as the radius, RL(2), of a sphere
with the same volume as that of the Roche lobe. This radius RL(2) has been
widely studied for different mass ratios (q = M1/M2).
Equation 2 by Eggleton (1983) is widely
used since it is valid for a wide range of mass ratios (
Sepinsky et al. (2007) studied the definition of RL(2) for eccentric binaries; they found the following generalization:
Where r12 is the distance between the two stars at a given time. Since we have that distance from our integration of the most efficient case, we can plot RL(2) as a function of time, as shown in Figure 5.

Fig. 5 Location of RL(2) as a function of time. RL(2) is the radius of the sphere with a volume equal to that of the Roche lobe of the system. See text for discussion.
We can calculate the maximum
We proceed as follows. First we assume that the secondary is a polytrope of index
3/2 (we assume a certain shape of the Roche Lobe). Also that the density around
the L1 point is given by equation 2.11 of Warner (1995),
We can estimate the mass transfer rate using equation 2.12 of Warner (1995),
where C is a dimensional constant ≈10-20 and
Therefore, we can calculate the maximum and minimum of the mass transfer rate by
using the values of
We now estimate the luminosity due to accretion (Warner 1995). First, we calculate the luminosity due to the so called hot spot (the place where the stream of stellar mass crosses the L1 point and collides with the disk):
where L(SP) is the luminosity due to the hot spot; the radius of the disk is
typically
With this equation for L(d) we can obtain the extreme values of
We can calculate the bolometric magnitude using
The observed change on magnitude at quiescence is ≈ 0.4 magnitudes when using a sinusoidal best fit, as shown in Figure 2, but the data points are quite disperse; so we also calculated the difference between the maximum and minimum magnitude of the observed data, finding 1.1 magnitude. The most efficient parameters model give us an expected change of magnitude of ≈ 0.29. We remind the reader that the latter is an order of magnitude estimate, with simplifications, assumptions and estimations.
4.Alternative Scenarios for the VLPP
One possible explanation to the VLPP is the cyclic magnetic variation (analogue to the Solar cycles) in the secondary star, which may lead to mass transfer variations. Long term variations have been observed in CVs, as mentioned in Richman et al. (1994) where they concluded that this explanation is plausible. But they found that the cycles did not show any strict periodicity and were decades long. In Table 3 of Mascareño et al. (2016) the magnetic cycle of medium to late M stars was found to be 7.1 years for a sample of stars of this type.
As pointed out at the end of § 3.1, in this research the secondary star on FS-Aur is
expected to be a very late M star; their internal structure is not the same as that
of a normal main sequence star counterpart with the same mass. Stars with
Bianchi (1992) and Hessman et al. (2000) found evidence of a possible relation between mass accretion variations and solar cycle type phenomena. The evidence showed variations on the timescales of decades on the overall system brightness and provided theoretical support for star-spots migrating to the L1 region (Howell 2004). This migration would help to correlate the star-spot to the changes in the position of the L1 point due to a possible third body.
Nevertheless, the magnetic cycles in very late M stars have not been studied in detail for secondaries in CVs; we recognise this mechanism as a plausible alternative to the mechanism proposed here.
5. Summary and Final Comments
We confirm the presence of VLPP with a refined period of 857 days based on 5 additional years (20 years total) of observations for FS Aur. This result also helps to confirm the authenticity of this signal.
We also revisit the triple CV hypothesis in which a massive planet, or a substellar object, pumps eccentricity into the inner binary orbit by secular perturbations. New parameters of mass, radius and temperature for the binary members of the CV are calculated and used to recalculate the most efficient parameters for the third body as defined earlier. The most efficient combination that explains the 857 day period is a third body with M3 =29MJ and P3/P2 =12.7 (P3 = 18.16 H). This new value is 1.7 times smaller than our previous estimation and is well within the limits of planetary masses. For example, the planet HD 169142b has a similar mass . All numerical calculations are made for a third body in an initial circular and planar orbit, as in CH2012.
We also explore more complicated models to study the secular perturbations of systems with eccentric and inclined orbits, using previous analytical results (Georgakarakos 2002, 2003, 2004, 2006, 2009). We find that as the eccentricity increases the most efficient candidate third body has a larger mass: M3 = 47MJ for an eccentricity of 0.2, and M3 = 48MJ for an eccentricity of 0.5 of the third body.
When the mutual inclination is explored the most efficient candidate for the third body has larger mass: if the inclination is 15o the expected most efficient mass is about M3 = 58MJ, but when the inclination is 30o the expected most efficient mass is now about M3 = 72MJ.
We consider other dynamical effects that might produce this VLPP, such as the first order post-Newtonian correction. We find that for the period of the pericentre circulation is 6812 days (18.65 yrs), that is, much larger than the 857 day period observed.
We calculated a first order estimation of the effect on the secular period of the
third object due to the mass transfer rate, and hence on the brightness of the
system; a change of magnitude of the order of only
We examine alternative scenarios for the VLPP. A possible explanation by a solar type magnetic cycle of the secondary cannot be ruled out, since the VLPP is only 2.346 years and most of the cyclic type magnetic periods in mid to late M stars are of the order of decades. However, there are no studies for the magnetic cyles of very late M stars in CVs to further test this hypothesis; hence, this alternative is a plausible one.
In summary, we find (a) that the new extended data confirm that there is a VLPP, but with a new value of 857 days; (b) the new data are consistent with being a triple-system; (c) combining such data with new initial conditions yields a reduction (from M3 = 50MJ to 29MJ) of the mass estimate for the most efficient third body candidate; (d) an order of magnitude estimation for the mass transfer rate and the brightness of the system, with the initial conditions used here, leads to a change in magnitude of 0.3. This value is 25% times smaller than the observed one, but we find that changes of less than 0.01% in the R(2) parameter can increase the change in magnitude up to the observed one.
We would like to thank all the amateur observers who do a great and hard job by collecting professional grade data with persistence. We are particularly indebted to Joe Patterson, who guides the amateur community engaged in CV monitoring and who made possible the dense observational coverage of . We acknowledge with thanks the variable star observations from the AAVSO International Database contributed by observers worldwide and used in this research. CC acknowledges UANL PAICYT grant. We appreciate the comments, suggestions and corrections by the anonymous referee, which helped us to greatly improve the quality and content of this research.











 nova página do texto(beta)
nova página do texto(beta)


