PACS: 81.07.-b; 81.07.Ta; 78.30.-j; 81.05.Dz
1. Introduction
CdTe semiconductor nanoparticles immersed in transparent matrices have currently many important applications in electrochemistry 1, photoelectricity 2, solar cells fabrication 3, chemical sensors 4, bio-labelling 5 etc. The achievement of desired particle sizes over the largest possible range, controlled particular sizes, and good crystallinity are some of the properties expected in nanocrystal growing methods. The transparent matrices can be solid or liquid and organic or inorganic, depending on their use and the growth method employed. Thus, hard matrices for CdTe such as silica 6 and soft ones like hydrogels 7 have been employed, which allow a large variety of applications. SnO2 is a transparent oxide with the property of possessing high electric conductivity that places the oxide in a special position as matrix for electronic devices design, as instance. At present, CdS nanoparticles embedded in SnO2 have been successfully utilized in photocurrent generation 8, and in solar cells based on CdTe nanoparticles immersed in SnO2 matrix have been already studied with good results 9. Nowadays, a lot of growing techniques exist, physical or chemical, to prepare semiconducting nanoparticles, which have found a great acceptance among the researches of wide-world. In the last four years several works have been publishe about CdTe nanoparticles immersed in SiO2, in which the good photoluminescent properties at energies larger than that of bulk CdTe have been reported 10,11,12.
In this work the preparation of CdTe nanoparticles by means of r.f. sputtering with radius in the range 2.4 - 7.0 nm is reported. Actually, a CdTe-SnO2 nanocomposite was grown on glass substrates. Within the framework of II-VI semiconductor quantum dots (QD) the sputtering growth technique offers controlled size distribution, also the preparation of CdTe crystallized in the metastable hexagonal wurtzite phase 13. Structural and optical studies include X-ray diffraction, transmission electron spectroscopy, optical absorption and Raman analysis to characterize the quantum confinement in the CdTe nanoparticles immersed in the also nanoparticulate SnO2 matrix, both undoped. The variation at room temperature (RT) of the main vibrational modes of wurtzite CdTe nanoparticles, when their size goes to small values, is studied. The main contribution of this the analysis of the optical properties of hexagonal CdTe, since there are few reports in this crystalline phase of this important semiconductor.
2. Experimental Details
The CdTe + SnO2 thin films were prepared on 7059 Corning glass substrates by means of the r.f. sputtering technique in an Ar ambient at 20 mTorr and at RT. The time for deposition was 180 min. The target was 5 cm2 of diameter and was prepared with mixed 99.999 % purity SnO2 and CdTe powders. The CdTe weight percentage in the target varied from 2% to 20% to get different nanoparticles size. After the growth the samples were annealed at 300°C in air during one hour. A variety of different crystallite size in the 4.8 - 14 nm range was obtained. Films have thickness of 200
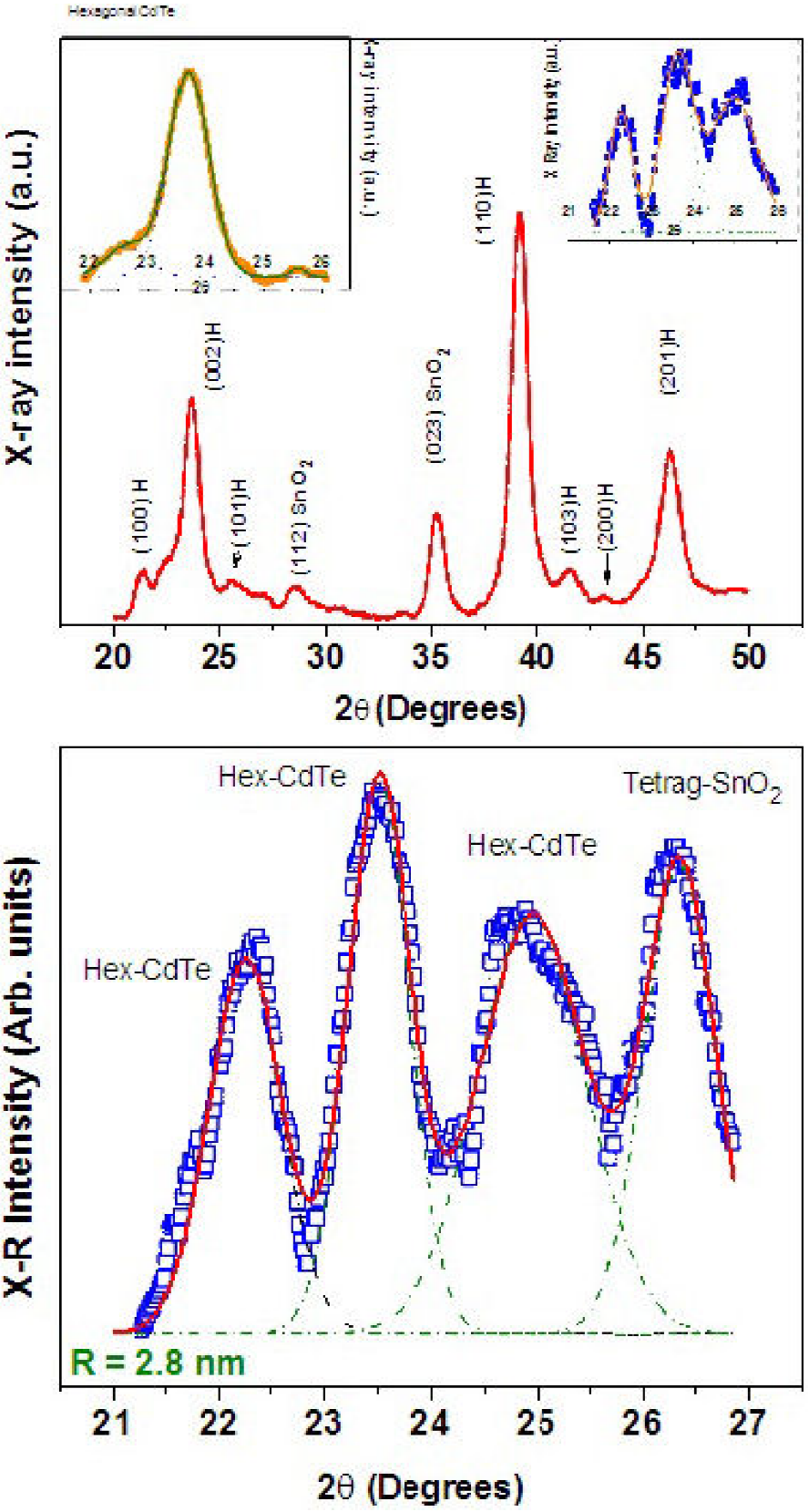
Figure 1. (a) Typical X ray diffraction (XRD) pattern of the WCdTe embedded in SnO2 matrix. Reflections labeled with H indicates CdTe in hexagonal wurtzite crystalline phase. XRD peaks corresponding to the tetragonal phase of the SnO2 matrix can be observed. Insets illustrate the deconvolution fitting process followed to calculate the nanoparticle radius. (b) Deconvolution of hexagonal CdTe and SnO2 broad X-ray diffraction bands. In this picture it can be appreciated that both types of nanoparticles have approximated the same average size.
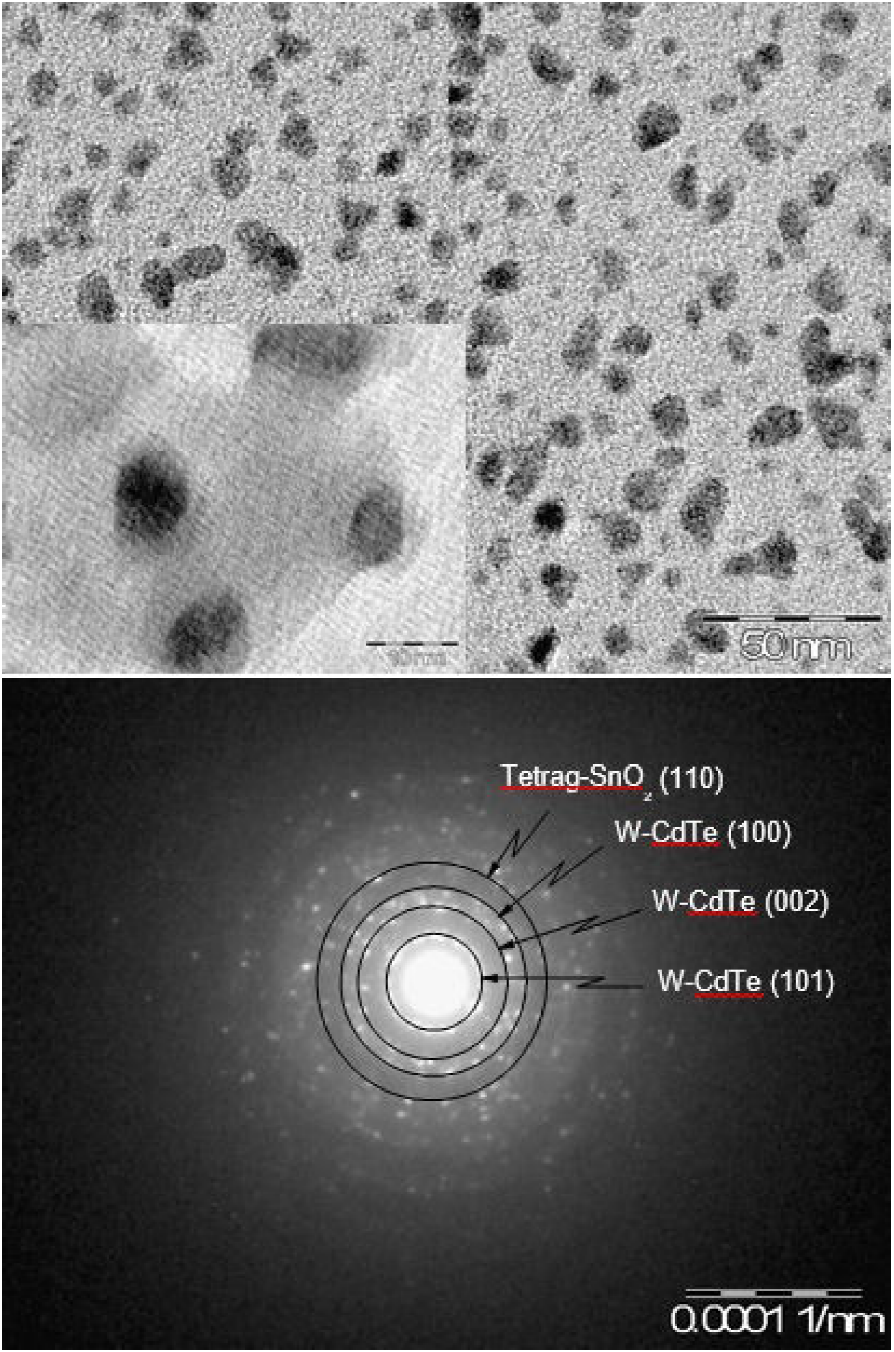
Figure 2. (a)TEM image of CdTe distribution of nanoparticles immersed in the SnO2 matrix for an average diameter of ~ 12 nm. The inset illustrates the TEM image of a detail of CdTe QD prepared with average size of ~ 4 nm, the bar scale is 10 nm. (b) Electron diffraction pattern of nanoparticulate W-CdTe and SnO2 matrix.
3. Results and Discussion
The crystalline structure of the CdTe nanoparticles immersed in SnO2 is the hexagonal wurtzite (W-CdTe) phase as observed in Fig. 1(a), where a typical XRD pattern of the CdTe + SnO2 nanocomposite, in the range 20
From the UV-Vis optical absorption spectra of the CdTe + SnO2 films and the relation (
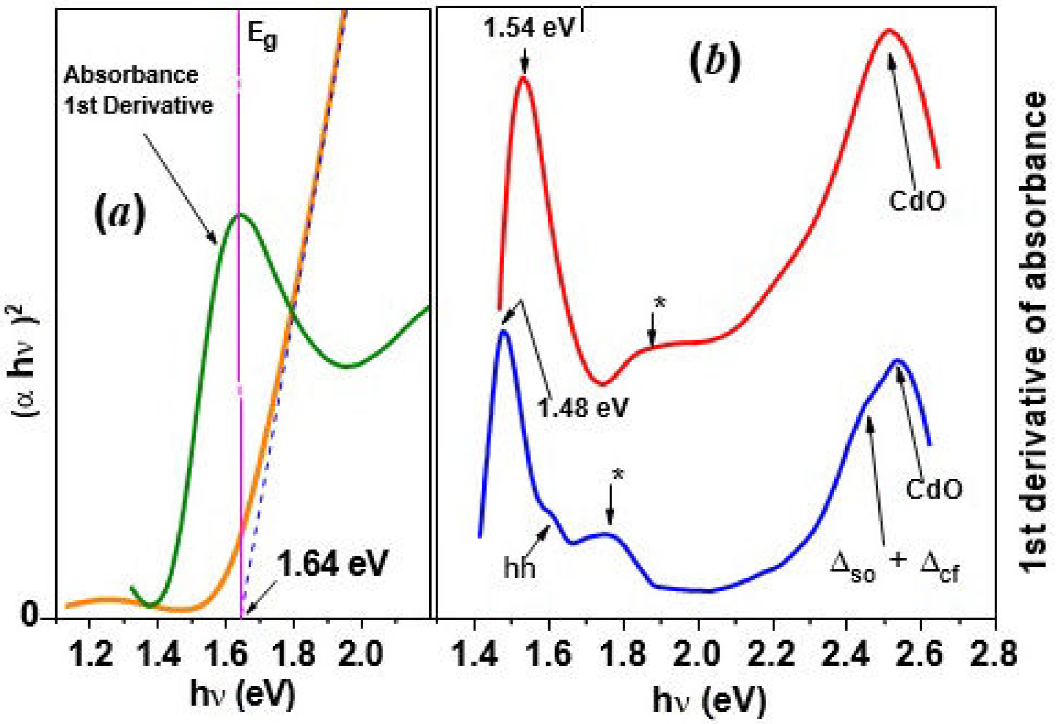
Figure 3. (a)Calculation of the first exited energy of electrons in the nanoparticle with R = 4.5 nm employing both the first derivative of absorbance spectra and the (
The second electronic transition due to the next discrete level has been identified with the second band and was indicated with other small arrow accompanied by an asterisk. The third transition observed in Fig. 3(b) is a well pronounced maximum around 2.5 eV, which has been identified by us that is originated from CdO formed at the interface CdTe-SnO216, since the direct band gap of CdO is ~ 2.5 eV 17. Other possible phases formed in the CdTe surface 14 as product of oxidation are TeO2 and CdTeO316,18, however these oxides have band gap values of ~ 3.8 and ~ 3.9 eV, respectively 19,20,21,22. Then, in our case, that a CdO layer has been formed in the CdTe/SnO2 interface is highly probable. A small feature in the bottom spectrum in Fig. 3(b), which was indicated by the “hh” label, is due to first electronic transition from the heavy-holes in the valence band 23. In this same spectrum a shoulder is observed at around 2.44 eV which is due to the spin- orbit plus the crystal field unfolding (
The first (
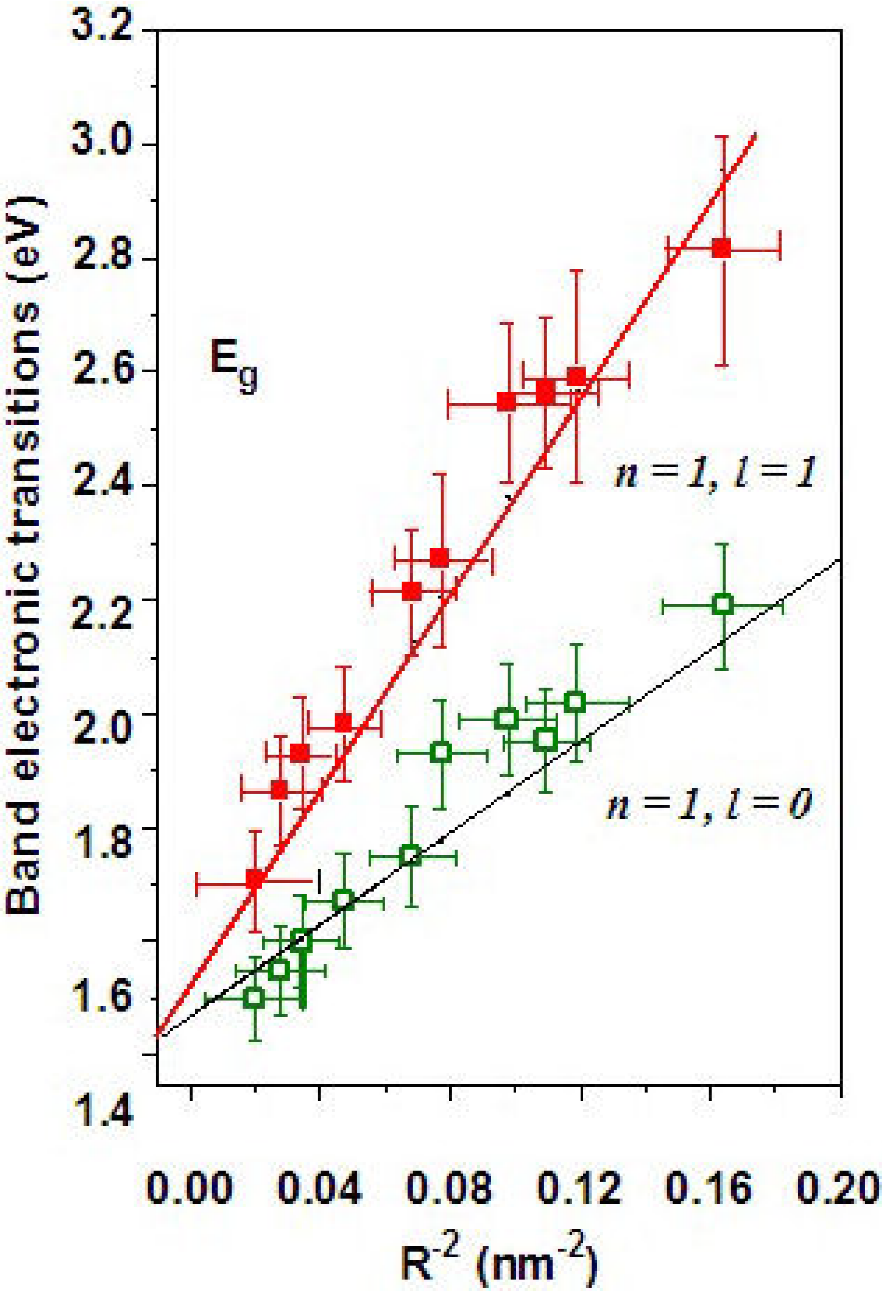
Figure 4. First two electronic transitions of W-CdTe versus the square inverse of nanoparticle radius.
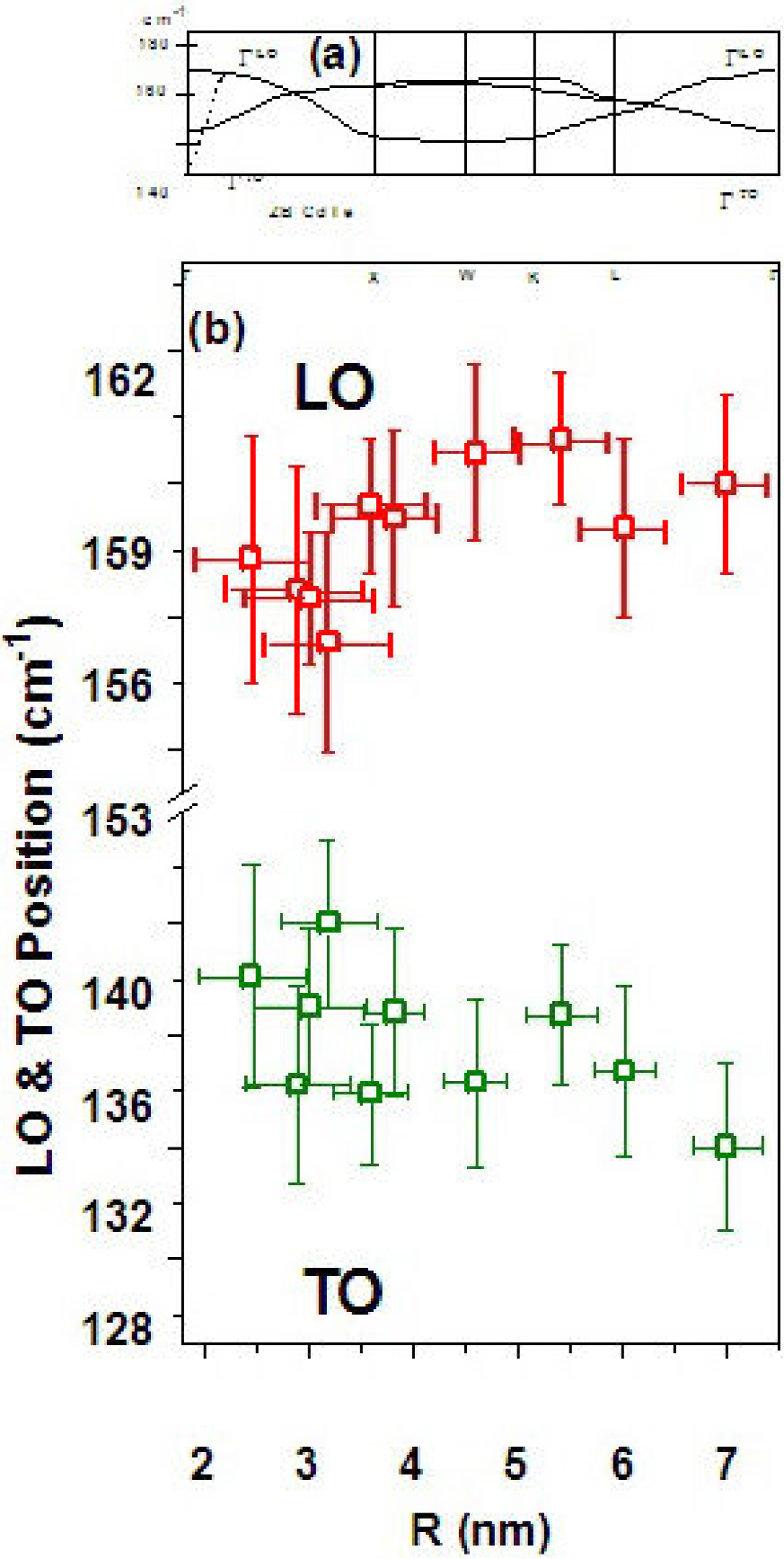
High resolution of CdTe Raman spectra was carried out in the set of samples. The Raman spectra of two CdTe representative samples (samples with
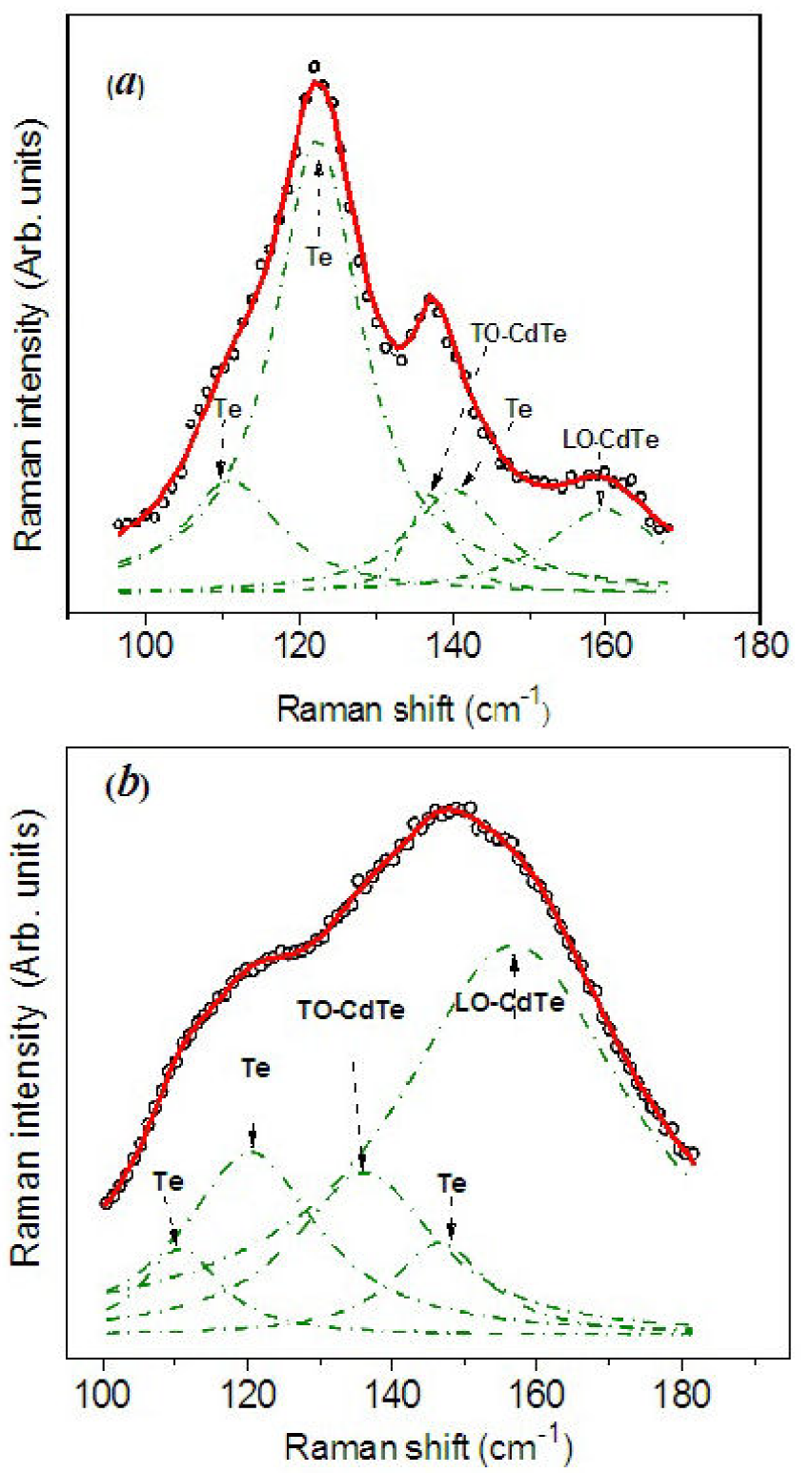
Figure 5. Raman spectra of two CdTe nanoparticles. (a) Deconvolution to separate the positions of the modes of Te and of the TO and LO modes of the CdTe nanoparticle with R = 5.4 0.4 nm. (b) Of sample with R = 2.4 0.5 nm.
4. Conclusions
Wurtzite CdTe nanoparticles embedded in SnO2 matrix in the radius range 2.4-7.0 nm were succesfully prepared by means of the r.f. sputtering technique. X-ray diffraction shows that W-CdTe and Tetragonal SnO2 nanocrystals have sizes of the same order. W-CdTe is the metastable phase of bulk CdTe, however for nanoparticles is a stable phase. The quantum confinement occurs in the strong regime as the Bohr radius for CdTe is 7.3 nm. From optical absorbance the first and second electronic transition were determined. In Raman spectra the LO and TO modes of W-CdTe were measured where, as expected from dispersion curves, the LO mode hardens and the TO softens when the radius of nanoparticles tends to lower values.











 nueva página del texto (beta)
nueva página del texto (beta)