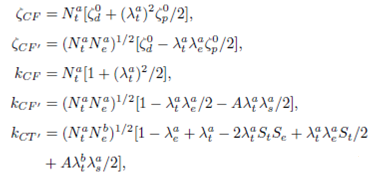1. Introduction
Palladium(II) complex K2PdCl4 has attracted considerable attention due to the medicinal properties as well as applications in drugs with high antitumoral and antibacterial activity1.Meanwhile, K2PdCl4 can act as a catalyst to afford an efficient, mild and environmentally friendly method in the synthesis of α-aminonitriles2. This material is also used in an increasing number of applications in chemical, electrical, electronic and glass industries and the manufacture of jewellery3. On the other hand,Cr3+ is a widely used dopant in various functional systems such as night-vision materials4, fiberoptic thermometers5, laser hosts6,7, photocatalysis8 as well as vivo imaging and drug delivery mediums9. Cr3+ is also essential for mammal metabolism with declining concentrations of both glycose and cholesterol in blood10, and its non-specific binding with DNA and other cellular components can possibly result in inhibition of transcription and replication of DNA11. In addition, Cr3+ as an environmental contaminant and various industrial and agricultural activities (especially in food and water) has been a focus in the relevant fields12,13.
Usually, the above properties and applications may strongly depend upon the electronic structures and local behaviors of Cr3+ in these systems, and the investigations on the local structures and behaviors of Cr3+ in K2PdCl4 are of scientific and practical significance. It is known that EPR spectroscopy is sensitive to the immediate environment around the paramagnetic impurities and able to reveal important microscopic information (e.g., defect structures such as occupation, strength of crystal-fields and local lattice distortions etc.) in the hosts. Recently, electron paramagnetic resonance (EPR) study was carried out for Cr3+ doped K2PdCl4 at liquid nitrogen temperature (LNT), and the spin Hamiltonian parameters (SHPs) were measured for the orthorhombic substitutional Cr3+ centre on K+ site (site I)14. So far, the above EPR experimental results for Cr3+ doped K2PdCl4 have not been theoretically explained, except that the d-d transition optical spectra were quantitatively analyzed based on the crystal-field theory [14]. Since this orthorhombic Cr3+ centre on the host K+ site in K2PdCl4 is quite different from the conventional tetragonal Cu2+ centre on square planar Pd2+ site, further theoretical investigations on the SHPs of this system can be helpful to understand the impurity behaviors and the properties of K2PdCl4 with transition-metal dopants and are of specific importance. The aim of this article is to propose satisfactory and uniform interpretations of the SHPs for the Cr3+ centre in K2PdCl4 by involving the local structure of the impurity based on the perturbation calculations of these parameters. The arrangement of this paper is the follows. In Sec. 2, the relevant theoretical formulas for the calculations of the SHPs are provided. The results are discussed in Sec. 3. The conclusion of the article is drawn in the last section.
2. Theoretical calculations
In this section, the theoretical calculations of the SHPs are performed for the Cr3+ centre in K2PdCl4. In the treatments, the contributions to the SHPs from both the crystal-field (CF) and charge-transfer (CT) mechanisms are included in view of significant covalency of the system. EPR measurements14 indicate that Cr3+ in K2PdCl4 occupies substitutionally the host K+ site and exhibits the local orthorhombic (D2h) site symmetry. For a 3d3 (Cr3+) ion under orthorhombically distorted octahedra, its ground orbital singlet A2g may yield ZFSs D and 𝐸 via the combination of the spin-orbit coupling and the orthorhombic CF interactions15.
2.1 Cluster approach treatments involving both the CF and CT contributions
In view of the high valence state of central ion Cr3+ and the strong covalency of ligand Cl-, the studied CrCl6 cluster may demonstrate strong covalency and CT contributions to the SHPs15-17. Based on the cluster approach18,19 involving both the CF and CT contributions, the spin-orbit coupling coefficients and the orbital reduction factors are expressed as follows:
Here ζ0d and 𝜁 𝑝 0 are, respectively, the spin-orbit coupling coefficients of the 3d3 ion and the ligand in free states. Nxγ and λxγ (or λxs) are the normalization factors and the orbital admixture coefficients, with the superscripts x (= a and b) denoting the anti-bonding and bonding orbitals and the subscripts 𝛾 (= t and e) labeling the cubic (Oh) irreducible representations T2g and Eg, respectively. The subscripts CF and CT represent the related quantities of the CF and CT mechanisms, respectively. A stands for the integral R ⟨χs|∂/∂x|χpx⟩ between the ligand 3s and 3p orbitals, with the reference impurity-ligand distance R. The molecular orbital coefficients N xγ and λxγ are usually determined from the normalization conditions, the orthogonality relationships, the approximate relationships for the anti-bonding orbitals and in terms of the effective covalency factor N based on the cluster approach18,19.
2.2 Perturbation formulas for an orthorhombically distorted 3d3 cluster
For this strongly covalent system, not only the contributions from the conventional CF mechanism (related to the anti-bonding orbitals) but also those from the CT mechanism (related to the bonding and non-bonding orbitals) affect significantly the 𝑔-shifts arising from the second-order perturbation term due to the combination of spin-orbit coupling and orbital angular momentum interactions18,19. As for ZFSs D and E, the CF contributions originate from the third- and fourth- order perturbation terms due to the combination of orthorhombic CF and spin-orbit coupling interactions or the off-diagonal parts of the inter-electronic repulsion interactions, while the CT ones arise mainly from the third order perturbation terms due to the combination of orthorhombic CF and spin-orbit coupling interactions. Utilizing the Macfarlane’s perturbation-loop method20,21 and involving the CT contributions to 𝑔 factors and the ZFSs 𝐷 and 𝐸, one can obtain the improved perturbation formulas of the SHPs for an orthorhombically distorted octahedral 3d3 cluster as follows:
The quantities Ds, Dt, 𝐷 𝜉 and 𝐷 𝜂 are the orthorhombic CF parameters. The corresponding denominators E i (I = 1 - 4 and 8)20,22 are the energy differences between the ground 4A2g and the excited 4T2g [t 2 2(3T1)e], 2T2g (t3 2), 2T2g [t2 2 (3T1)e], 4T1g[t2 2 (3T1)e] and 2T1g [t2 2 (3T1)e] states, respectively. These denominators are expressed in terms of the cubic CF parameter Dq and Racah parameters B and C from the strong field approach23,24:
For an octahedral 3d3 cluster, the CT level can be determined as En≈30000[χ(L)-χ(M)]+14B (cm-1)15. Here X(L) and X(M) are the optical electronegativities of ligand and central ions, respectively.
3. Calculations for the orthorhombic Cr3+ centre in K2PdCl4
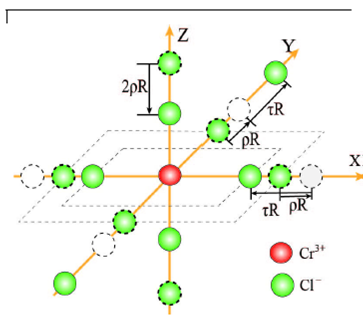
The host K+ site in K2PdCl4 is surrounded by a tetragonally compressed chlorine octahedron, with the cation-anion distances Rx=Ry≈5.7689 Å and Rz≈3.2191 Å [14]. Occupation of the impurity Cr3+ on host K+ site can lead to the significant lattice modifications of the local impurity-ligand distances due to the remarkable discrepancies between charge and ionic radii of Cr3+ and K+. For convenience, the local structure of the Cr3+ centre is described by a relative axial compression ratio 𝜌 and a relative perpendicular bond length variation ratio τ (see Fig. 1). Usually, the effective (average) impurity-ligand bond length R in the impurity centre may differ from that of the host cation-anion distance RH(=(R∥H+2R⊥H)/3≈4.919 Å14) in K2PdCl4 since the ionic radius ri (= 0.615 25) of the impurity Cr3+ is much smaller than the radius rh (=1.38 Å25) of the host K+. The investigations based on experimental superhyperfine constant and extended X-ray absorption fine structure (EXAFS) measurements26 reveal that the empirical relationship R≈RH+(ri-rh)/2 is approximately valid for an impurity ion in crystals. In view of the size mismatch, the reference bond length R(≈4.537 Å) is obtained for the studied system. Thus, the local impurity-ligand distances along X, Y and Z axes in the impurity centre can be expressed in terms of the reference bond length R and the local distortion parameters ρ and τ as follows:
Utilizing the local geometry and the superposition model27-31 the orthorhombic CF parameters can be determined as:
Here t2≈3 and t4≈5 32 are the power-law exponents. A2 (R) and A4 (R) are the intrinsic parameters, with the reference distance R. The relationships A4 (R) = (3/4)Dq and 32-34 for 3d ions under octahedral CFs based on the superposition model are reasonably employed here.
In the light of the optical spectral measurements for Cr3+ in K2PdCl414 and similar chlorides35, the cubic field parameter Dq≈1851 cm-1 and the effective covalency factor N≈0.82 are obtained for the studied impurity centre. Utilizing the Slater-type self-consistent field wave functions36 and the distance R, the group overlap integrals (Sdpt≈0.00005 , Sdpe≈0.0002 and Sds≈0.00004) and the integral A≈2.1138 are calculated. The related molecular orbital coefficients are determined for both CF and CT mechanisms from the cluster approach 18-19 : Nat≈0.67, Nea≈0.670, λta≈0.702, λea≈0.688, λsa≈0.138 and Ntb≈0.663, Neb≈0.724, λbt≈-0.712, λbe≈-0.605 and λbs≈-0.121. Appling the free-ion values ζ0d (Cr3+)≈ 273 cm-137 and ζ0p (Cl-) ≈ 587 cm-138, the spin-orbit coupling coefficients and the orbital reduction factors are obtained for both mechanisms from Eq. (1): ζCF≈280 cm-1, ζCF'≈88 cm-1, ζCT'≈396 cm-1 and kCF≈0.835, kCF'≈0.44 and kCT'≈0.634. The Racah parameters B and C in Eq. (3) can be expressed in terms of the free-ion values B0 (≈1030 cm-137 and C0 (≈3850 cm-137 of Cr3+ as: B≈B0N2 and C≈C0N2 39. The CT level En can be obtained from the values χ(Cl-)≈2.4 and χ(Cr3+) ≈1.9 15. Substituting these values into Eq. (4) and fitting the calculated SHPs to the observed values, the optimal local distortion parameters ρ and τ are obtained:
The corresponding theoretical SHPs (Calc.c) are collected in Table 1. The results (Calc.a) based on the host structural data of K3+ site in K2PdCl4 and inclusion of both the CF and CT contributions and those (Calc.b) based on the above optimal local distortion parameters and inclusion of merely the CF contributions are also listed in Table 1.
Table 1 The ZFSs D and E (in 10¡4 cm¡1) and g factors for Cr3+ in K2PdCl4.
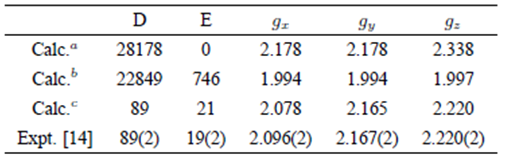
aCalculations based on the host structural data of K+ site in K2PdCl4 and inclusion of both the CF and CT contributions.
bCalculations based on the optimal local distortion parameters ρ and τ and inclusion of merely the CF contributions.
cCalculations based on the optimal local distortion parameters ρ and τ and inclusion of both the CF and CT contributions.
4. Discussion
Table 1 indicates that the theoretical SHPs (Calc. c) based on the local distortion parameters 𝜌 and 𝜏 show better agreement with the experimental data than those (Calc. a) based on the host structural data of K+ site and those (Calc.b) based on omission of the CT contributions. Thus, the measured EPR spectra for the Cr3+ centre in K2PdCl4 are satisfactorily explained in a uniform way. Meanwhile, the information about the local distortion around the impurity Cr3+ is theoretically determined by analyzing the experimental ZFSs. The following points are discussed here.
(1)As compared with the axial compression ratio (ρH≈18.6%) and nearly zero perpendicular distortion ratio (τH≈0) of the host K+ site in K2PdCl4, the impurity Cr3+ centre exhibits smaller axial compression (ρ≈11.1 %) and much larger perpendicular distortion (τ≈11.7 %) and hence a more regular ligand octahedron, corresponding to the very small D and E. Thus, the much (two or three order in magnitude) larger D and zero E (Calc.a) based on the structural data of host K+ site can be understood. The microscopic mechanisms of the local lattice deformations are illustrated as the much stronger Cr3+-Cl- interaction than the host K+-Cl- combination due to the much higher impurity valence state. Meanwhile, the long reference impurity-ligand distance R(≈4.537 Å) and hence low force constant of the Cr3+-Cl- bonds also account for the above remarkable Cr3+-Cl- bond length variations with respect to the host K+-Cl- bonds. As a result, the axial and perpendicular distortions are considerably decreased and increased, respectively, from host K+ site to the impurity centre. As one might deliberately assign the measured EPR signals to Cr3+ on the square planar Pd2+ site, the calculated D would be much (two or three order in magnitude) larger than the experimental value, and the above remarkable discrepancy cannot be removed by adjusting the related spectral parameters or local distortion parameters. So, Cr3+ may tend to occupy the octahedral K+ site instead of the square planar Pd2+ site and is quite different from the conventional tetragonal Cu2+ centre on Pd2+ site in K2PdCl440. This point can be illustrated by the dissimilar electron configurations of Cu2+ (3d9) and Cr3+ (3d3), which tend to exhibit square planar [CuX4] and octahedral [CrX6] groups by means of dsp2 and d2sp3 hybrid orbitals41,42. Interestingly, similar octahedral trivalent Fe3+ (3d5) centre on K+ site was also reported for iron doped K2PdCl443, which can also be ascribed to the octahedral [FeCl6] group by means of sp3d2 hybrid orbitals41,42. It seems that electronic configuration plays a more important role than size or charge mismatch in occupation of transition-metal impurities in K2PdCl4. So, the impurity Cr3+ occupying K+ site rather than Pd2+ site is understandable in physics.
(2)When the CT contributions are ignored, the calculated g factors and ZFSs (Calc. b) are smaller and much larger than the experimental data. For the studied [CrCl] group, the system demonstrates strong covalency due to the covalent ligand Cl- and central ion Cr3+ with high valence state and much larger ζp0(Cl-) ≈587 cm-138 than ζ0d (Cr3+) ≈273 cm-137. Substantially, the host K2PdCl4 may exhibit strong covalency due to the optical electronegativity ≈2.2 15) of Pd2+ comparable with that ≈3.0 15) for Cl-. This can be illustrated by the effective covalency factor N (≈0.82) and the obvious orbital admixture coefficients (≈0.2∼0.7) from the cluster approach. In fact, the contributions to g-shifts ΔgCT from the CT mechanism are opposite in sign and twenty-one times larger in magnitude compared with ΔgCF from the CF mechanism. As for the ZFSs, the CT contributions DCT and ECT are opposite in sign and almost the same (characterized by the ratios |DCT/DCF and /ECF≈ 99.3%) in magnitude with respect to the corresponding DCF and ECF. Thus, the CT contributions are found to be important and should be included in the EPR analysis.
(3)The errors of the present theoretical calculations may be analyzed as follows. First, the final results may be brought forward some errors due to the approximations of the theoretical model and formulas based on the spin Hamiltonian theory, in which only the contributions from the nearest neighbor ligands are considered whereas the influences of the ions in the outer ligand spheres are omitted. For the present impurity Cr3+ in tetragonal K2PdCl4 lattice, the electric fields from the rest ions of the crystal could be anisotropic and bring forward some influences on the total crystal fields acting upon Cr3+. To some extent, the opposite contributions to the crystal fields arising from the relevant ions (e.g., Pd2+, Cl-; K+, Cl-; etc.) may partially cancel each other due to opposite charges and lead to insignificant effects on the total crystal fields of Cr3+ because of their successively farther distances ≫R≈4.537 Å) from the impurity. Second, the error of the reference impurity-ligand distance R may arise from the empirical relationship in terms of the difference between the ionic radii of the impurity and the replaced cation26. Fortunately, the influences of R is actually cancelled in the calculations of the orthorhombic CF parameters in Eq. (5), and the above error of R would merely affect the related group overlap integrals and lead to even smaller errors (no more than 0.5%) for the resultant SHPs and the optimal local distortion parameters 𝜌 and 𝜏. Third, substitution of K+ by Cr3+ with two extra positive charge may induce some means of charge compensators (e.g., one Pd2+ vacancy or two K+ vacancies) and might slightly modify the local structure of the impurity centre. However, the non-axial charge compensators would lead to considerable perpendicular orthorhombic distortion and significant E, which was obviously inconsistent with the experimental tiny Evalue14. On the other hand, the possible axial compensators (e.g., Pd2+ and K+ vacancies) might bring forward important effect on the charge distribution of the impurity centre. However, the negative effective charges of these possible compensators would repel the axial ligand(s) Cl- towards the central Cr3+, inducing much more axial compression of the impurity centre and hence larger magnitude of D. Nevertheless, this is actually in disagreement with the observed very small D14. So, the possible charge compensators may occur far from the impurity and its influence on the local structure is very small and negligible. Finally, the empirical superposition model and ratio ¯A2(R)/¯A4(R)≈10.8 for the intrinsic parameters of other systems would also result in some errors. Based on the calculations, when the ratio varies within the widely accepted range of 9∼12, the errors for the SHPs and the optimal distortion parameters are estimated to be less than 4%. In fact, the above treatments need to be justified for the certain case, especially those with nearby charge compensation. Therefore, in order to perform more accurate studies of the SHPs for the present system, more powerful density function theory (DFT) calculations are to be adopted in the future work.
5. Conclusions
The SHPs and local structure for Cr3+ in K2PdCl4 are theoretically analyzed from the perturbation calculations for an orthorhombically distorted 3d3 cluster. The impurity Cr3+ is found not to occupy the host Pd2+ site but to locate at the octahedral K+ site, associated with the relative axial compression ratio ρ (≈ 11.1%) and the relative perpendicular bond length variation ratio τ (≈ 11.7%). So, the impurity centre exhibits smaller axial compression distortion and much larger perpendicular orthorhombic distortion than the host K+ site in K2PdCl4 and hence a more regular ligand octahedron, corresponding to the very small D and E. The contributions to g-shifts ΔgCT from the CT mechanism are opposite in sign and twenty-one times larger in magnitude compared with 𝛥 𝑔 𝐶𝐹 from the CF mechanism. For the ZFSs, the CT contributions DCT and ECT are opposite in sign and almost the same in magnitude with respect to the corresponding DCF and ECF. The microscopic mechanism for this unique Cr3+ centre on octahedral K+ site, which is quite dissimilar to the conventional tetragonal Cu2+ centre on square planar Pd2+ site, is illustrated in view of the d2sp3 hybrid orbitals.











 text new page (beta)
text new page (beta)