Área de estudio

El estudio se realizó en varios bosques templados del ejido Cebadilla de Dolores, ubicado en la cordillera de la Sierra Madre Occidental, 56 km al suroeste del municipio Madera, en el estado de Chihuahua (Figura 1). El predio tiene una superficie de 38 442.77 ha, de las cuales 4 895.22 son terrenos forestales y 4 573.15 ha se destinan al aprovechamiento maderable. El clima corresponde al templado subhúmedo con lluvias en verano, la altitud fluctúa de 1 175 a 2 510 m (^{García, 2004}). Las comunidades vegetales más importantes están constituidas por bosques mezclados con especies del género Pinus y Quercus, además de algunas especies arbustivas (^{Consultoría Ambiental Agropecuaria Forestal y Financiera [CAAFF], 2015}).

Figura 1 Localización geográfica del ejido Cebadilla de Dolores, Madera, Chihuahua, México. 

Variables utilizadas

Las variables utilizadas fueron el diámetro normal y el área basal que se relacionaron con la edad. Para estimar el diámetro normal se midieron los radios en cada rodaja con una regla Nobrand ^® graduada en mm y se multiplicaron por dos (Ecuación 1). A partir de los diámetros normales, se obtuvieron las áreas basales (Ecuación 2) (^{Buendía-Rodríguez et al., 2019}).

Donde:

dni = Diámetro normal a la edad i (cm)

r = Radio de las secciones

abi = Área basal a la edad i (m²)

Datos

Los datos se tomaron de 27 árboles de Pinus durangensis mediante un muestreo selectivo y destructivo en diferentes condiciones de sitio. Por árbol se obtuvieron rodajas a 1.30 m de la base con una motosierra STIHL ^® MS 172, 3/8"P y el número de árbol se etiquetó como información de control (^{Klepac, 1983}). Además, se contabilizó el número de anillos desde el centro hacia la periferia; con la información se generó una base de datos de diámetros normales para todas las edades. Debido a que los análisis troncales son un método de muestreo destructivo, solo se consideraron 27 árboles por la disposición para su derribo. Sin embargo, al utilizar las series de tiempo de crecimiento, se logró tener información suficiente para modelar el crecimiento del diámetro normal y el área basal.

Modelos utilizados

Para describir el crecimiento en diámetro normal y área basal de Pinus durangensis, basado en los anillos de crecimiento de la rodaja de 1.3 m, se realizó un primer ajuste con siete modelos de crecimiento mediante la técnica de Modelos No Lineales Generalizados. La estructura de los modelos utilizados (ecuaciones 3 a 9) fue empleada por ^{Zeide (1993)}:

M1, Chapman-Richards:

M2, Hossfeld IV:

M3, Gompertz:

M4, Weibull:

M5, Logístico:

M6, Monomolecular:

M7, Korf:

Donde:

yij = Diámetro normal o área basal j en el árbol i

α0, α1, α2 = Parámetros para estimar

e = Función exponencial

tij = Edad j en el árbol i

εij = Error aleatorio j en el árbol i

Dado que las edades de los árboles a los cuales se les realizaron los análisis troncales variaron entre 29 y 67 años, los diámetros y áreas basales de todos los árboles se proyectaron a la edad máxima registrada, con la finalidad de obtener una base de datos simétrica y que la modelación se basara en el mismo intervalo de la variable dependiente como una serie de tiempo equilibrada (^{Harvey & Shephard, 1993}; ^{Parzen, 1961}). La proyección de cada una de las variables mencionadas se hizo mediante los modelos anamórfico y polimórfico en diferencias algebraicas y derivados del modelo de Chapman-Richards (M1; Ecuación 3) (^{Richards, 1959}), ya que en un análisis preliminar fue el más eficiente, de acuerdo con los estadísticos de ajuste utilizados (Ecuación 10 y 11):

M8, Chapman-Richards-Anamórfico:

M9, Chapman-Richards-Polimórfico:

Donde:

α0, α1, α2 = Parámetros para estimar

e = Función exponencial

y1, y2 = Diámetro normal o área basal en el estado 1 y 2

t1, t2 = Edad en el estado 1 y 2

ln = Logaritmo natural

Posteriormente, el modelo ajustado con el rendimiento más eficiente del sistema de jerarquización (^{Kozak & Smith, 1993}) fue reparametrizado con efectos fijos y aleatorios, esto con el fin de representar la variabilidad del crecimiento en diámetro normal y área basal del árbol a través de modelos no lineales con efectos mixtos (^{Pinheiro & Bates, 2006}; ^{Pinheiro et al., 2009}). Los modelos mixtos se recomiendan cuando hay datos correlacionados como en este caso.

Con el modelo base más eficiente en un análisis preliminar y comparativo (estadísticos del sistema de jerarquización), se formularon tres modelos no lineales con efectos mixtos (MEM) basados en la formulación de modelos no lineales con efectos fijos y aleatorios (^{Pinheiro et al., 2009}). En el primer modelo solo se consideró el efecto aleatorio del parámetro de la asíntota “α0” (M10; Ecuación 12), mientras que en el segundo se incluyeron los efectos aleatorios del parámetro de la asíntota combinado con el parámetro de escala “α0, α1” (M11; Ecuación 13) y en el tercero, los efectos aleatorios del parámetro de la asíntota combinado con el parámetro de forma “α0, α2” (M12; Ecuación 14).

M10:

M11:

M12:

Donde:

yij = Diámetro normal o área basal j en el árbol i

α0,α1 y α2 = Parámetros fijos

e = Función exponencial

tij = Edad j en el árbol i

α0i, α1i, α2i = Parámetros aleatorios a nivel árbol

εij = Error aleatorio j en el árbol i

Los modelos no lineales de efectos mixtos consideraron el término del error de acuerdo con ^{Pinheiro y Bates (2006)} y la unidad de estudio fue el árbol. Para cada variable, la formulación genérica fue la siguiente (Ecuación 15) (^{Corral et al., 2019}):

Donde:

yij = Diámetro normal o área basal j en el árbol i

f = Función del modelo de crecimiento (^{Richards, 1959}) de 1×p covariables

φi = Vector de parámetros para el árbol i

εij = Término del error, el cual se asume independiente y normalmente distribuido con media cero y varianza σ ²

∅i = Vector de parámetros r×1 (r es el número de parámetros en el modelo) específico para el árbol i

λ = Vector p×1 de los parámetros fijos

bi = Vector de parámetros aleatorios asociados con el árbol i

Ai, Bi = Matrices de diseño r×p y r×q para los efectos fijos y aleatorios específicos para el árbol i, respectivamente

Ajuste de modelos

La estimación de los parámetros para los modelos base se realizó a través de modelos lineales generalizados en el paquete “gnls” del software R versión 4.3.3 (^{R Core Team, 2024}), mientras que los MEM fueron ajustados a través de máxima verosimilitud en el paquete “nlme” del software R versión 4.3.3 (^{R Core Team, 2024}) bajo los algoritmos desarrollados por ^{Pinheiro y Bates (2006)}. Estos procedimientos han sido estudiados con éxito en modelos de altura-diámetro (^{Corral et al., 2019}).

Estadísticos de ajuste

La bondad de ajuste de los modelos se midió con el Coeficiente de Determinación ajustado (R ² ), el Índice de Ajuste (FI), la Raíz del Error Cuadrático Medio (RMSE), el Error Estándar de la Estimación (SEE), el Error Estándar Relativo de la Estimación (RSEE), el Error Promedio (E), el Error Promedio Relativo (RE), el Criterio de Información de Akaike (AIC), el Criterio de Información Bayesiano (BIC) y el logaritmo de la verosimilitud (LogLik). Estos estadísticos han sido utilizados en sistemas de ecuaciones de ahusamiento y volumen de manera satisfactoria (^{Quiñonez-Barraza et al., 2019}; ^{Zhao et al., 2018}). Además, los modelos base fueron evaluados con un sistema de jerarquización con los estadísticos propuestos por ^{Kozak y Smith (1993)} y aplicado por ^{Quiñonez-Barraza et al. (2019)} en la evaluación de ecuaciones de ahusamiento y volumen.

Normalidad de los efectos aleatorios

La normalidad de los estimadores de los parámetros aleatorios fue evaluada con la prueba de normalidad de Shapiro-Wilk (^{Hanusz et al., 2016}; ^{Shapiro & Wilk, 1965}) a un nivel de significancia de 1 %. Esto se relaciona con la teoría de MEM (^{Pinheiro et al., 2009}).

Proyección de tendencias de crecimiento

La proyección de los datos y la simetría de las tendencias de crecimiento se realizó con el modelo base M1 (Ecuación 3), las ecuaciones anamórfica (M8; Ecuación 10) y polimórfica (M9; Ecuación 11); aunque ambos modelos mostraron proyecciones aceptables, el modelo polimórfico (M9; Ecuación 11) generó mejores representaciones para las dos variables estudiadas, el cual asume que las tasas de crecimiento en los diferentes sitios donde se desarrollaron los árboles fueron diferentes, y se relaciona con las bases de las ecuaciones en diferencia algebraica (^{Bailey & Clutter, 1974}).

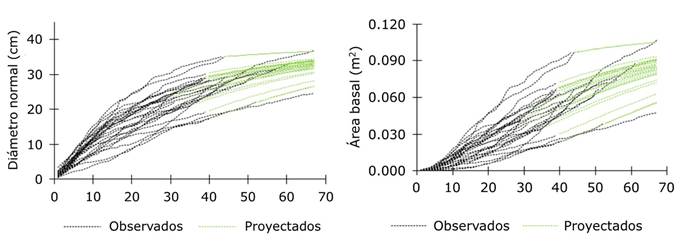
En la Figura 2 se ilustran las tendencias para el diámetro normal y el área basal. La generación de bases de datos asimétricas ofreció la posibilidad de modelar el crecimiento para una serie de tiempo equilibrada y simétrica (^{Harvey & Shephard, 1993}). Las tendencias evidenciaron los ritmos de crecimiento en las variables de estudio. Los hallazgos son similares a los referidos por ^{Tamarit-Urias et al. (2021)} en el crecimiento en diámetro para Pinus montezumae Lamb. en bosques del estado de Puebla, México.

Figura 2 Proyección de las trayectorias de crecimiento del diámetro normal y área basal a los 67 años con la ecuación anamórfica y polimórfica del modelo M1. 

Relación diámetro normal-edad y área basal-edad

En el Cuadro 1 se ordenan los estimadores de los parámetros para los siete modelos de crecimiento que se ajustaron a la relación diámetro normal-edad y área basal-edad. Se observa que todos los parámetros fueron significativamente diferentes de cero a un nivel de significancia de 1 %, tanto para el diámetro normal como para el área basal. Por ello, los modelos estudiados por ^{Zeide (1993)} y utilizados en otras investigaciones (^{Aguirre-Bravo y Smith, 1986}; ^{Quiñonez et al., 2015}) permitieron modelar el crecimiento del diámetro normal y el área basal de manera satisfactoria para Pinus durangensis.

En el Cuadro 2 se muestran los estadísticos de ajuste y la calificación que obtuvo cada uno de los modelos de crecimiento en diámetro normal y área basal en su forma básica, en la cual el menor valor de calificación corresponde al modelo con mejor ajuste (^{Kozak & Smith, 1993}). Con base en lo anterior, el modelo de Weibull (M4; C=25) fue el de mejor ajuste en diámetro, seguido de los modelos de Chapman-Richards (M1; C=28), Hossfeld IV (M2; C=30), Logístico (M5; C=36), Gompertz (M3; C=40), Monomolecular (M6; C=59), y Korf (M7; C=61). Independientemente del mejor ajuste del modelo de Weibull, se decidió, dada la flexibilidad y amplio uso, aplicar el modelo M1 para representar las estimaciones del diámetro normal.

Por otro lado, el modelo de Chapman-Richards (M1; C=24) fue el que tuvo el mejor ajuste en área basal, seguido de los modelos de Hossfeld IV (M2; C=30), Gompertz (M3; C=38), Weibull (M4; C=40), Logístico (M5; C=42), Monomolecular (M6; C=48), y Korf (M7; C=58). También, se optó por utilizar el modelo M1 para representar las estimaciones del área basal.

Los resultados de este estudio son semejantes a los registrados por ^{Hernández et al. (2020)}, quienes evaluaron los modelos de crecimiento en diámetro normal, área basal, altura total y volumen fustal con los modelos de Chapman-Richards, Schumacher, Hossfeld I y Weibull para árboles individuales de Pinus pseudostrobus Lindl. y Pinus oocarpa Schiede ex Schltdl. en Guerrero y Estado de México. En su investigación definieron al modelo de Chapman-Richards como el mejor para estimar el área basal de Pinus oocarpa con una R ² de 0.9154 y una RMSE de 0.0096 m². De igual forma, ^{Corral y Návar (2005)} ajustaron ecuaciones de crecimiento e incremento en diámetro normal para especies de Pinus en la región de El Salto, estado de Durango, México; concluyeron que el modelo de Chapman-Richards presentó los crecimientos e incrementos mayores a nivel grupo de árboles e individualmente para Pinus durangensis, con una R ² de 0.70 y RMSE de 3.29 cm.

^{Domínguez-Calleros et al. (2017)} ajustaron los modelos de crecimiento Log Normal, Chapman-Richards, von Bertalanfy, Logístico y Gompertz, también basados en las formulaciones de ^{Zeide (1993)} con ecuaciones integrables en tiempo, y determinaron que el mejor ajuste fue el de Chapman-Richards; aunque concluyeron que es necesario realizar nuevas investigaciones para revisar los límites en los que se aplican las suposiciones con el ajuste de los modelos a series de tiempo.

Los resultados del estudio aquí descrito también concuerdan con los presentados por ^{Ramirez et al. (2014)}, quienes compararon modelos de crecimiento en diámetro normal para Eucalyptus urophylla S. T. Blake, usaron datos de 55 árboles y concluyeron que el modelo de crecimiento de Chapman-Richards presentó un menor error estándar, con base en el AIC determinaron que este modelo fue el mejor.

Relación diámetro normal-edad y área basal-edad con efectos mixtos

En el Cuadro 3 se listan los estimadores de los parámetros y las propiedades estadísticas para las tres combinaciones de modelos de crecimiento con efectos mixtos ajustados a la relación diámetro normal-edad y área basal-edad, con base en la formulación de modelos no lineales con efectos mixtos (^{Corral et al., 2019}; ^{Pinheiro et al., 2009}). Para este caso, todos los estimadores de los parámetros fueron significativamente diferentes de cero a un nivel de significancia de 1 %. También, se muestran los parámetros asociados a la varianza de los efectos aleatorios y del término del error para las combinaciones de parámetros mixtos y variables de estudio.

En el Cuadro 4 se resumen los valores de los estadísticos de ajuste de los MEM para predecir el crecimiento en diámetro y área basal. En general, los tres modelos ajustados para la especie de interés mostraron bondad estadística satisfactoria, aunque la mejor explicación resultó del ajuste del modelo M12 (Ecuación 14) al asociar los parámetros fijos α0 y α2 con los aleatorios α0i y α2i de forma aditiva (α0+α0i) y (α2+α2i) para predecir el crecimiento en diámetro normal y área basal en función de la edad, respectivamente. Estos estadísticos demostraron que los MEM son superiores a los modelos con solo efectos fijos (^{Corral et al., 2019}). Y son mejores porque consideran la variabilidad dentro de árboles y entre árboles.

En la Figura 3 se observa el comportamiento gráfico de las estimaciones y los datos observados del diámetro normal y el área basal contra la edad para cada una de las combinaciones del ajuste de modelos de efectos mixtos. Con la inclusión de efectos aleatorios, en todos los casos se asume la variabilidad en las series de crecimiento a nivel árbol individual.

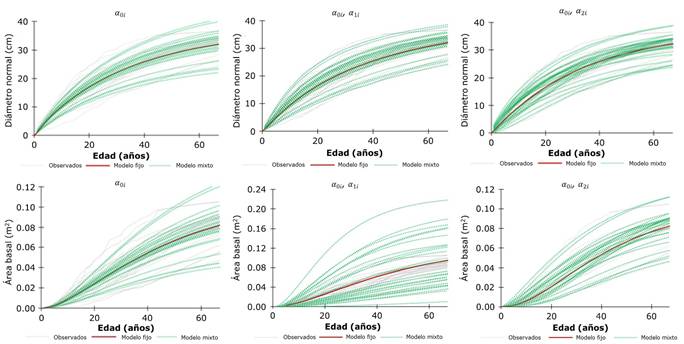
Figura 3 Comportamiento del diámetro normal y área basal para cada una de las combinaciones del ajuste de modelos de efectos mixtos. 

Los resultados del mejor ajuste para el modelo de crecimiento en diámetro normal coinciden con los referidos por ^{Quiñonez-Barraza et al. (2015)}, quienes evaluaron tres modelos de crecimiento en Diferencia Algebraica (ADA) y tres en Diferencia Algebraica Generalizada (GADA) para predecir el crecimiento en diámetro normal, en función de la edad para seis de las principales especies comerciales de pino en Durango, con información de 44 302 virutas de crecimiento, recolectadas en 15 609 sitios del inventario forestal. Sus resultados indican que el modelo polimórfico de Chapman-Richards (^{Richards, 1959}) predice mejor el crecimiento en diámetro de Pinus lumholtzii B. L. Rob. & Fernald con una R ² de 0.99 y una RMSE de 0.63 cm, mientras que para Pinus ayacahuite C. Ehrenb. ex Schltdl., un modelo GADA basado en Verhulst-Logística predice mejor el crecimiento en diámetro normal con una R ² de 0.99 y una RMSE de 0.64 cm.

De forma semejante a los resultados de este estudio, ^{Arteaga-Martínez (2000)} identificó que el modelo de Chapman-Richards fue el que mejor se ajustó y representó el crecimiento en diámetro de Pinus pseudostrobus, con un ajuste estadístico regular, pero aceptable para su utilización práctica (R ² =0.8870).

Los resultados de este estudio también fueron similares a los de ^{Hernández et al. (2020)}, quienes ajustaron cuatro modelos de crecimiento en diámetro normal para tres especies de Pinus en Chihuahua, México. Para ello, usaron una muestra de 82 árboles, y determinaron que los ajustes de los cuatro modelos (Chapman-Richards, Hossfeld I, Schumacher y Weibull) probados para el crecimiento en área basal fueron buenos, con coeficientes de determinación de 0.96 a 0.98, respectivamente y la RMSE de 0.004 a 0.006.

^{Calvillo et al. (2005)} describieron el crecimiento e incremento en diámetro normal y área basal de Pinus herrerae Martínez a través de análisis troncales de 34 árboles recolectados en la región de Ciudad Hidalgo, Michoacán, México; probaron los modelos de crecimiento de Chapman-Richards, Gompertz, Logístico, Schumacher, Weibull y Exponencial; definieron que el mejor modelo para describir el crecimiento en diámetro fue el de Gompertz (RMSE=26.8730 y R ² =0.9697) y para el área basal el Logístico (RMSE=0.00037 y R ² =0.9374).

Las formulaciones de MEM hicieron posible identificar la variabilidad del crecimiento de diámetro normal y área basal para la fuente de árbol de cada serie de tiempo simétrica y se asumió la variación por medio de efectos fijos y aleatorios para las combinaciones de los parámetros del modelo base de Chapman-Richards (^{Richards, 1959}), y asociado a la teoría de MEM (^{Corral et al., 2019}).

Pruebas de normalidad a los parámetros aleatorios

Las pruebas de normalidad efectuadas a los parámetros aleatorios de los modelos de diámetro normal y área basal, ajustados como MEM, indicaron que el parámetro aleatorio que representa a la asíntota a nivel árbol para las dos variables de estudio fue normal, con valores superiores al nivel de significancia de 1 %. Para el modelo del diámetro normal se calculó un valor de 0.15, mientras que para el de área basal fue de 0.14 (Cuadro 5). En ambos casos no se rechaza la hipótesis nula y se asume que los parámetros aleatorios correspondientes a α0i para los 27 árboles estudiados siguen una distribución normal teórica con media igual a cero y varianza conocida (^{Pinheiro et al., 2009}). Además, las series de tiempo de los análisis troncales y la asimetría en tiempo permitieron la obtención de resultados satisfactorios.

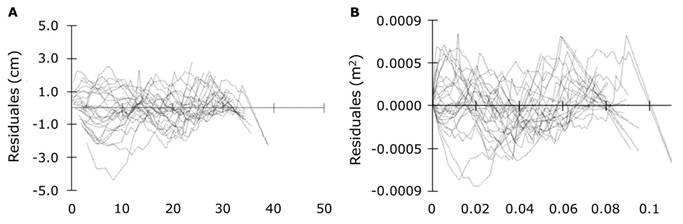
El análisis gráfico de los residuales contra los valores predichos corroboró el nivel de desempeño del modelo M12 para predecir el crecimiento en diámetro normal y área basal (Figura 4). La tendencia de los residuales se reconoció sensiblemente simétrica alrededor de la línea del cero. Tales residuales se presentan como series de tiempo para cada árbol y se asume la variabilidad del sitio de muestreo.

A = Diámetro normal; B = Área basal.

Figura 4 Valores residuales frente a valores predichos de crecimiento del diámetro normal y del área basal con la inclusión de efectos mixtos.