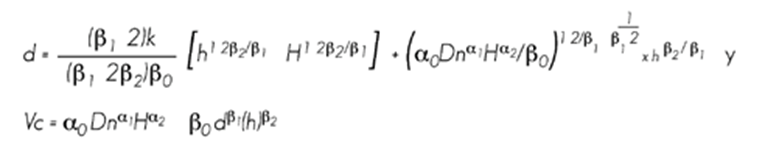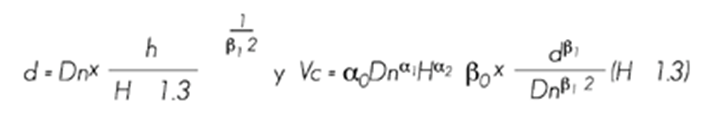Introducción

La estimación precisa de las existencias volumétricas y la distribución de productos son esenciales para planear la aplicación de prácticas silvícolas en las intensidades adecuadas, y en el momento oportuno, e indispensable para obtener el mayor retorno económico posible de la inversión efectuada en el establecimiento, mantenimiento y aprovechamiento de las plantaciones forestales comerciales (PFC), o en las actividades de aprovechamiento en bosque natural (^{Cancino, 1993}; ^{De la Fuente et al., 1998}; ^{Zepeda y Acosta, 2000}).

El uso correcto de herramientas silvícolas, precisas para el manejo orientado a obtener el máximo rendimiento de los productos permite la evaluación de las actividades silvícolas, en cualquier momento de su desarrollo (volumen e ingreso), y determina el punto óptimo de cosecha (ciclo de corta y turno) (^{Cancino, 1993}; ^{De la Fuente et al., 1998}; ^{Zepeda y Acosta, 2000}; ^{Tamarit et al., 2013}).

En el cálculo del volumen total o por tipo de producto en cada unidad de superficie, previo a la cosecha, se requiere contar con un sistema preciso de cubicación del arbolado en pie, y una ecuación que determine el patrón de troceado, con el objetivo de maximizar el volumen o el valor de los productos obtenidos en los bosques naturales o las PFC (^{Cancino, 1993}; ^{De la Fuente et al., 1998}; ^{Tamarit et al., 2013}). Dicho sistema es una herramienta básica en los inventarios forestales y en la planeación de las actividades de manejo (^{Corral-Rivas y Návar-Cháidez, 2009}).

A partir de las funciones de ahusamiento es factible describir la forma del fuste, calcular la altura comercial para cualquier diámetro límite deseado, estimar el volumen total, el volumen comercial y el volumen por trozas individuales por árbol; de manera general para una especie o plantaciones. Lo anterior permite realizar cálculos de las existencias volumétricas por unidad de superficie o rodal (^{Clutter et al., 1983}; ^{Cruz- Cobos et al., 2008}).

De acuerdo a su complejidad matemática, estas funciones se clasifican por el número de variables utilizadas y la cantidad de coeficientes involucrados (^{Quiñonez-Barraza et al., 2014}), en modelos basados en polinomios, de tipo trigonométrico, exponenciales y segmentados (^{Tamarit et al., 2013}). Ajustar de manera simultánea el ahusamiento con el volumen total resulta en una estimación del volumen comercial de forma compatible, ya que los valores de los parámetros obtenidos integran la forma del árbol y el volumen correspondiente a diferentes secciones (^{Demaerschalk, 1972}; ^{Clutter, 1980}).

Dada la importancia que tienen las proyecciones de distribución de productos en la planeación del manejo y la valoración económica, para bosques naturales o PFC; además de la solidez matemática de los modelos de ahusamiento y volumen comercial al ajustarlos de forma simultánea, se han utilizado para modelar en México especies como P. arizonica Engelm., en Chihuahua (^{Pompa et al., 2009}); P. pseudostrobus Lindl., en Nuevo León (^{Tapia y Návar, 2011}); P. patula Schiede ex Schltdl. & Cham., en Hidalgo (^{Hernández et al., 2013}; ^{Uranga- Valencia et al., 2015}); y P. arizonica, P. ayacahuite Ehrenb. ex Schltdl., P. durangensis Martínez, P. leiophylla Schiede ex Schltdl. & Cham, P. teocote Schiede ex Schltdl. & Cham. (^{Quiñonez-Barraza et al., 2014}), P. oocarpa Schiede ex Schltdl. y P. douglasiana Martínez (^{López et al., 2015}), en Durango.

El objetivo del presente estudio fue generar un sistema compatible de ahusamiento-volumen comercial (d-Vc) para árboles individuales de Pinus greggii Engelm. en plantaciones forestales de Metztitlán, Hidalgo, México. El sistema compatible está integrado por un modelo de ahusamiento, uno de volumen total (Vt) y otro de volumen comercial (Vc).

Materiales y Métodos

Las plantaciones forestales de P. greggii están ubicadas en el ejido Fontezuelas, municipio Metztitlán, Hidalgo, entre los 20°29 ́ de latitud N y 98°54 ́ de longitud O, a una altitud que varía entre 2 000 y 2 500 m. Se localizan dentro de la provincia del Eje Neo-volcánico Transversal y la subprovincia del Carso Huasteco (^{Inegi, 1985}); con suelos de las unidades Feozem háplico y Regosol eútrico (^{Inegi, 1992}). El clima es templado semi-seco (^{García, 1988}); la región hidrológica corresponde a la RH26 Río Pánuco, sub cuenca río Moctezuma y microcuenca Hermosillo-Fontezuelas (^{Inegi, 1985}).

Se obtuvo información del análisis troncal de 24 árboles de P. greggii distribuidos estratégicamente para cubrir toda la variabilidad de formas y tamaños resultado del crecimiento de estos árboles, como lo indican ^{Torres y Magaña (2001)}, con el fin de mejorar el intervalo de aplicación de las ecuaciones generadas.

La toma de datos se efectuó mediante un muestreo destructivo, semejante a lo realizado por ^{Tamarit et al. (2013)} y ^{Hernández et al. (2013)}. Consistió en el derribo y troceo del arbolado; las mediciones fueron diámetro normal (Dn), diámetro con corteza (d) y alturas (Hm) a distancias de 1, 1.5, 2 y 2.55 m de acuerdo con las condiciones de forma del árbol y los productos comerciales que pudieran resultar; se inició a la altura del tocón (Ht) hasta la altura total (H). En el caso de la cubicación de trozas individuales se utilizó la fórmula de Newton y la del cono para la punta, mientras que el volumen total por individuo se estimó con el método de trozas traslapadas propuesto por ^{Bailey (1995)}.

Se auditó, corrigió y depuró la base de datos, mediante gráficas de las variables de ahusamiento y volumen acumulado, se observó el comportamiento de la información y la tendencia lógica, tal como lo realizaron ^{Pompa et al. (2009)}, ^{Tamarit et al. (2013)} y ^{Hernández et al. (2013)}. Se analizaron tres sistemas compatibles de ahusamiento-volumen comercial seleccionados de la literatura (^{Fang y Bailey, 1999}; ^{Lenhart y Clutter, 1971}), los cuales se probaron y evaluaron para describir el perfil fustal en árboles de P. greggii; y se muestran a continuación:

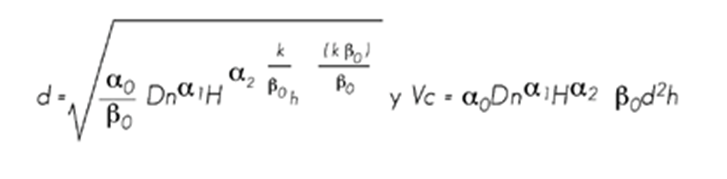
1) ^{Fang y Bailey (1999)} caso 1-a

2) General de ^{Fang y Bailey (1999)}

3) ^{Lenhart y Clutter (1971)}

Estos sistemas compatibles de ahusamiento-volumen comercial cumplen con la condición de que h = H cuando d = 0 y pueden ser utilizados para la predicción del diámetro a cualquier altura en el árbol; donde h = H-Hm y k = π/40000, cuando el diámetro está en metros.

El ajuste se realizó como lo indican ^{Fang y Bailey (1999)} y ^{Fang et al. (2000)}, con el modelo de volumen total de Schumacher-Hall para mejorar la estimación de los parámetros, obtener de manera más rápida la convergencia del sistema y hacer más precisa la significancia de los estimadores. Para evitar problemas de convergencia en el ajuste estadístico en la estimación de los parámetros, se empleó un valor numérico de delta = 0.001, que junto con una variable indicadora en la punta del árbol para h = H, cuando d = 0 evitaron que el modelo ajustara en cero y se perdiera un dato; por consiguiente, la capacidad de ajuste cerca de la altura total o diámetro cero.

Los sistemas compatibles se ajustaron por medio del procedimiento MODEL y el método de máxima verosimilitud (FIML) en el paquete estadístico SAS/ETS^® (^{SAS, 2008}); procedimiento que permite la estimación de los parámetros de manera simultánea, y se muestra normalidad de la frecuencia de los residuos, minimiza la varianza y asume una media igual a cero (^{Gujarati, 2004}), a partid de una distribución normal e independencia en los errores (^{Bruce et al., 2003}).

La evaluación y selección del mejor sistema compatible se llevó a cabo con los estadísticos de bondad de ajuste comúnmente utilizados, como el coeficiente de determinación ajustado (R²_aj) a y la raíz del cuadrado medio del error (RCME) (^{Prodan et al., 1997}; ^{Corral-Rivas et al., 2007}).

Una vez seleccionado el mejor modelo, se verifico de forma gráfica la homocedasticidad de los residuos. Los problemas de heterocedasticidad se corrigieron con una función que pondera la varianza de los residuales (^{Crecente et al. , 2009}), por medio de una función exponencial basada en la variable combinada (Residual/((dn²H)^ϕ)^0.5) de acuerdo a la metodología sugerida por ^{Harvey (1976)}, en la que el valor del parámetro φ proviene de la regresión línea del logaritmo natural de los residuales en función de la variable combinada (Dn²H ).

La autocorrelación de los errores se midió con la prueba de Durbin-Watson (DW), tal como lo sugieren ^{Augusto et al. (2009)}; ^{Pompa-García et al., (2009)} y ^{Hernández et al. (2013)}; y para corregir el problema de autocorrelación en los modelos que lo requirieran, se incluyó un modelo de tipo autorregresivo en tiempo continuo CAR(X) (^{Zimmerman y Nuñez-Antón, 2001}), aplicando retardos (pxr), tanto en ahusamiento como en volumen comercial, con la finalidad de obtener valores del estadístico Durbin-Watson (DW) cercano a 2 (^{Barrio et al., 2014}), en alguna de las dos variables. Además, se graficaron los datos observados contra los predichos de ahusamiento y volumen comercial para verificar el sesgo porcentual de la muestra, con respecto a las estimaciones.

Resultados y Discusión

Los parámetros en todos los sistemas compatibles resultaron altamente significativos con un nivel de confiabilidad mayor a 95 % y errores estándar aproximados (Eea) bajos, situación semejante a lo obtenido por ^{Hernández et al. (2013)} al utilizar los mismos sistemas para P. patula en Zacualtipán, Hidalgo (Cuadro 1).

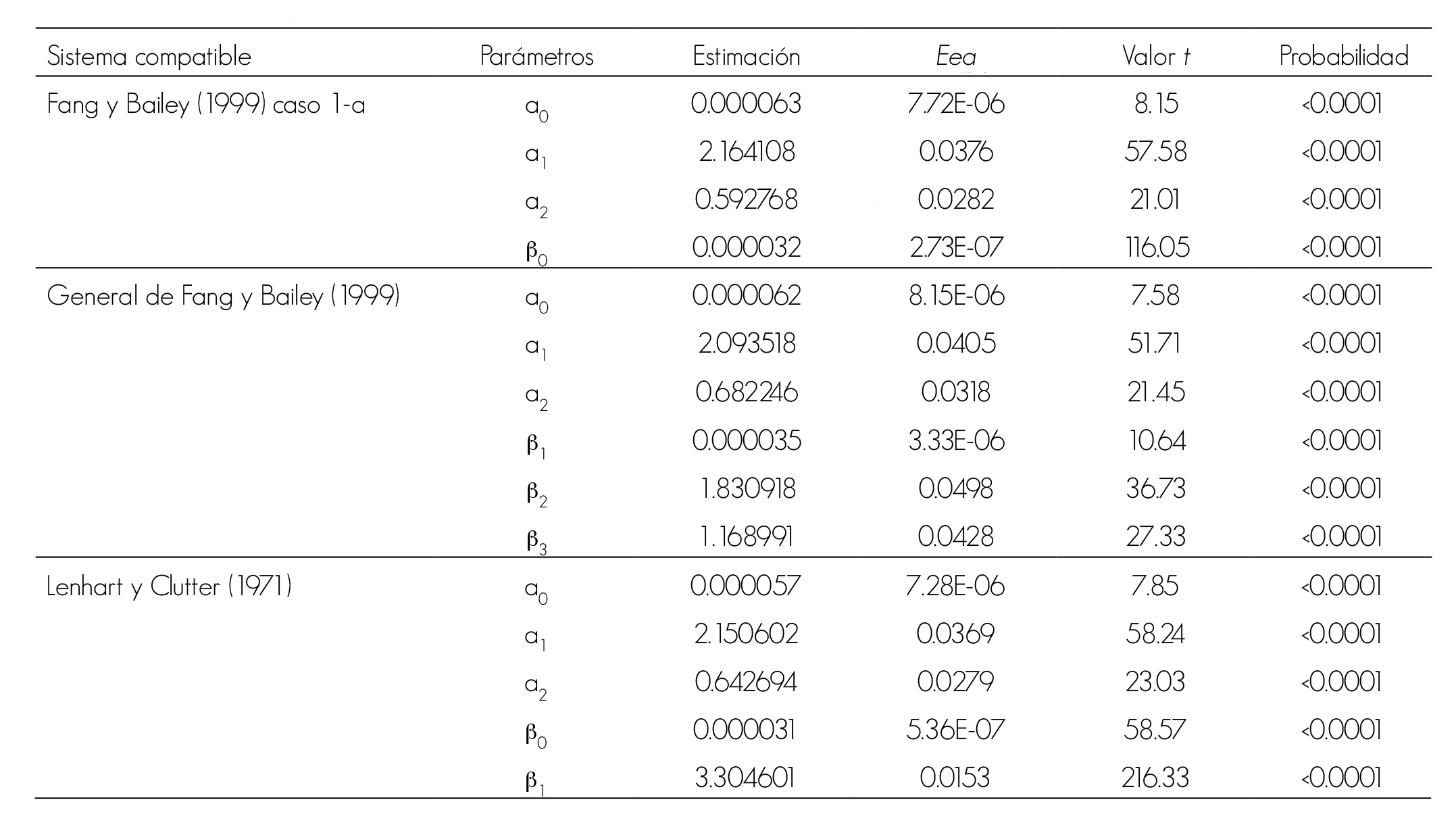
Cuadro 1 Valores de los parámetros en los sistemas compatibles de ahusamiento-volumen comercial utilizados para Pinnus greggii Engelm. en Metztitlán, Hidalgo. 

El modelo explícito de volumen total de Schumacher-Hall en los tres sistemas compatibles tuvo valores en los parámetros muy semejantes, solo con diferencias atribuibles al ajuste simultáneo de los modelos. Al comparar el volumen total calculado para la muestra y la estimación del volumen total, mediante los parámetros a ₀ , a ₁ y a ₂ de la ecuación de Schumacher-Hall, se tiene que el sistema general de ^{Fang y Bailey (1999)} arroja valores más precisos, ya que sustituyó solo 0.02 % del volumen total, en el total de la muestra, mientras que, el sistema de ^{Lenhart y Clutter (1971)} en 0.87 % y el de ^{Fang y Bailey (1999)} caso 1-a, lo sobreestima en 0.16 %. En los tres sistemas compatibles, el sesgo promedio en la estimación del volumen total respecto al volumen real es menor de 0.0022 m³ por individuo.

Con base en los criterios de bondad de ajuste se aprecia que el modelo general de ^{Fang y Bailey (1999)}, estadísticamente, es más estable para los datos utilizados, tanto en la descripción del fuste como en el volumen comercial y total (Cuadro 2). Este modelo explica de mejor manera la variabilidad total de ambas variables, debido a que los coeficientes de determinación ajustados, en los dos casos, son mayores que los otros sistemas, además de presentar los menores valores en la SCE y la RCME. Dichos valores son similares a los registrados por ^{Pompa et al. (2009)} al ajustar sistemas compatibles para P. arizonica en el suroeste de Chihuahua.

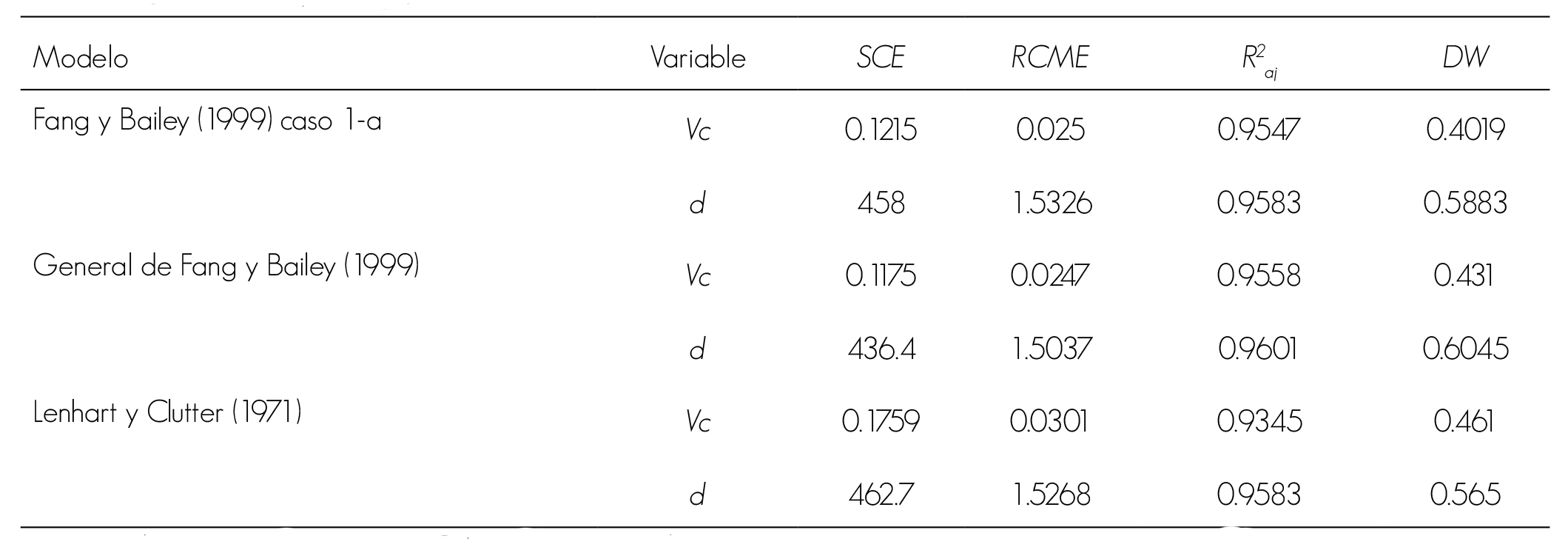
SCE = Suma de cuadrados del error; RCME = Raíz cuadrada media del error; R² _aj = Coeficiente de determinación ajustado; DW = Valor de la prueba de Durbin-Watson.

Cuadro 2 Estadísticos de bondad de ajuste de los tres sistemas de ahusamiento-volumen comercial utilizados para Pinus greggii Engelm. en Metztitlán, Hidalgo 

Al verificar los supuestos de regresión del modelo general de ^{Fang y Bailey (1999)}, que resultó ser estadísticamente el mejor, el valor de la prueba de Shapiro-Wilk (SW) indica normalidad de la frecuencia de los residuos (SW>0.93); sin embargo, los residuales de volumen comercial se distribuyeron de forma heterocedástica y el valor de la prueba de Durbin-Watson (DW) de autocorrelación fue de 0.43 para el ahusamiento y de 0.60 para el volumen comercial; en ambas casos menor a 1.5, lo cual es una violación de estos supuestos de regresión.

Una vez corregidos los problemas de heterocedasticidad y autocorrelación, se ajustó, nuevamente, el modelo general de ^{Fang y Bailey (1999)}, con ello se obtuvo una mejora estadística considerable (Cuadro 3). El valor de La prueba de normalidad de Shapiro-Wilk fue de 0.98 (α=<0.0001) y los residuales se comportaron de manera homocedástica, mientras que la prueba de DW para detectar la autocorrelación fue de 1.95 para ahusamiento y 1.16 para el volumen comercial.

SCE = Suma de cuadrados del error; RCME = Raíz cuadrada media del error; R² _aj = Coeficiente de determinación ajustado; p1r y p2r = Parámetros correspondientes al modelo autoregresivo de tiempo continuo (CAR(2)) aplicado para corregir la autocorrelación del sistema compatible de ahusamiento-volumen comercial.

Cuadro 3 Estadísticos de bondad de ajuste y valores de los parámetros del sistema compatible general de ^{Fang y Bailey (1999)} para Pinus greggii Engelm. en Metztitlán, Hidalgo 

Al graficar las estimaciones realizadas con el sistema compatible, se presenta una tendencia apropiada de los datos de ahusamiento y de volumen comercial (Figura 1 a y b), semejante a lo registrado por ^{Rodríguez y Broto (2003)} al analizar diversos modelos de perfil del fuste y hacer estudios de cilindridad de los árboles de Populus x euroamericana (Dode) Guinier en Navarra, España; así como, a lo citado por ^{Fassola et al., (2007)} al ajustar funciones de perfil de exponente variable y posterior ajuste de modelos de volumen compatibles para Eucalyptus grandis W. Hill. ex Maiden en Mesopotamia, Argentina; y por ^{Lara (2011)}, quien aplicó funciones de ahusamiento para, posteriormente, derivar el modelo de volumen comercial compatible para Tectona grandis L. en la zona costera de Ecuador.

Figura 1 Diámetro estimado (a) y volumen comercial acumulado con respecto a la altura sobre el fuste (b) para Pinus greggii Engelm. en Metztitlán, Hidalgo. 

Los valores predichos con el sistema compatible general de ^{Fang y Bailey (1999)}, con respecto a los datos observados presentan una tendencia lineal recta del ahusamiento (^{Fassola et al., 2007}; ^{Lara, 2011}) y el volumen comercial (^{Tamarit et al., 2013}) (Figura 1a y b), la cual es deseable en este tipo de estudios (Figura 2a y 2b).

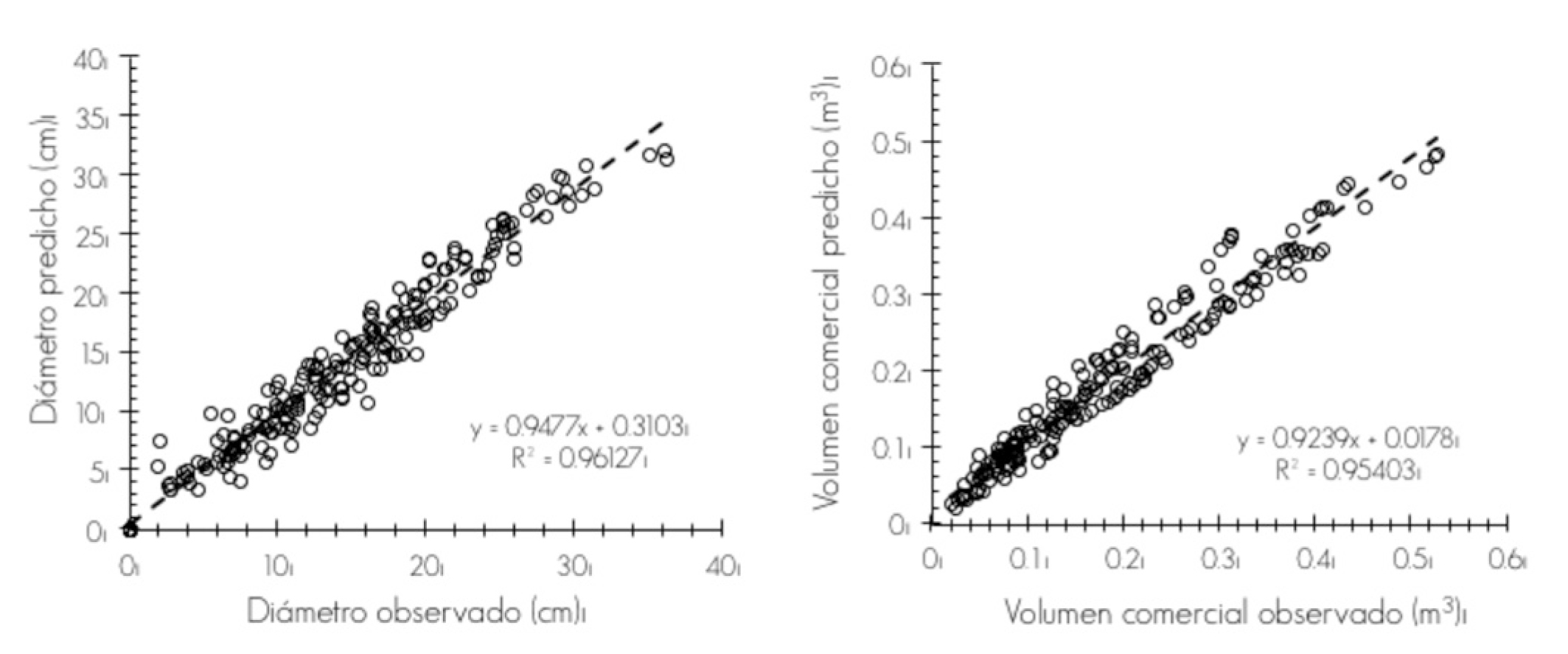
Figura 2 Comparación del diámetro y volumen observado contra los predichos de diámetro (a) y volumen comercial (b) del sistema compatible general de ^{Fang y Bailey (1999)} para Pinus greggii Engelm. en Metztitlán, Hidalgo. 

El coeficiente de determinación entre los valores predichos y observados indica que la descripción del perfil de los árboles por el sistema tiene una diferencia agregada en porciento para toda la muestra de 3.8 en ahusamiento y de 4.6 para volumen comercial; con un promedio en el sesgo por estimación de 0.017 y 0.020, respectivamente para cada variable (Figura 2a y 2b). Los sesgos son inferiores a los citados para el ahusamiento por ^{Návar y Domínguez (1997)} al emplear cuatro modelos de perfil fustal para Pinus brutia Ten., P. halepensis Mill., P. eldarica Medw. y P. estevezii (Martínez) F. P. Perry; ^{Corral et al. (1999)} al utilizar cinco modelos de perfil para P. cooperi C. E. Blanco, P. durangensis, P. engelmannii Carr., P. leiophylla y P. herrerae Martínez; ^{Tapia y Návar (2011)} en P. pseudostrobus con cinco modelos de ahusamiento.

El sesgo para el volumen comercial es semejante al documentado por ^{Quiñonez et al. (2014)} con sistemas compatibles de d-Vc para P. arizonica, P. ayacahuite, P. durangensis, P. leiophylla y P. teocote.

En el sistema compatible seleccionado, se observó que la predicción del diámetro a diferentes alturas tiende a presentar problemas en alturas menores o iguales a 0.3 m (altura de tocón), y a subestimar ligeramente los diámetros por debajo del primer tercio del árbol. Situación semejante a la observada en Ecuador por ^{Lara (2011)} y en México por ^{Tamarit et al. (2013)} para Tectona grandis. Al considerar que las partes bajas del arbolado pueden ser medidas de manera directa con mayor precisión, lo ideal es contar con herramientas que realicen estas estimaciones precisas en las partes altas, para conocer la distribución de productos, el diámetro mínimo y el volumen resultante (^{Rodríguez y Broto, 2003}; ^{Tamarit et al., 2013}).

Con los resultados del presente estudio se pueden realizar descripciones del perfil del árbol, así como estimaciones precisas del volumen total y volumen comercial en plantaciones de P. greggii, para la proyección de la distribución de productos maderables destinados a un mercado diferenciado.

Conclusiones

El sistema compatible de ahusamiento y volumen comercial de ^{Fang y Bailey (1999)}, es el que mejores estimaciones genera para describir el perfil de los árboles de P. greggii en las PFC evaluadas y se puede usar de manera confiable para predecir el diámetro a cualquier altura y su respectivo volumen, además es compatible con la ecuación de volumen total.

La información obtenida es una herramienta valiosa para los análisis de datos provenientes de inventarios forestales, particularmente, en la predicción de la distribución de productos por árbol o unidad de superficie de las plantaciones, y la valoración económica dentro de un mercado diferenciado de los productos maderables del aprovechamiento forestal.

Debido a que las actividades silvícolas aplicadas en las PFC afectan la forma del árbol y, por consiguiente, la distribución de productos, la constante actualización de esta información es fundamental en la planeación del manejo forestal sostenible para P. greggii