Introduction
Understanding directional and nondirectional intermolecular interactions in the crystal lattice and its application to design supramolecular architectures with favorite chemical and physical features is the finaltarget of crystal engineering. The crystal engineering of inorganic/organic compounds via intermolecular forces is considered a traditional synthesis against novel synthesis through covalent bonds [1-4]. Crystal engineering is a research area with goal of designing synthons that conserve intact from one lattice structure to another, which guarantees predict ability and generality [5-7]. To justify the design of new supramolecular structures and methodologies for crystal synthesis, non-covalent interactions including hydrogen bonds [8-10], halogen bonds [11-13], the π⋯πstacking [14], C−H⋯𝜋, cation/anion⋯π, and lone-pair⋯π [15] play essential roles in formation and stabilization of solid-state architectures. Thus, recently, “non-classical” interactionshave become a noteworthysubject for study as they have been proven to be equal or even dominating contributors to inorganic-organic crystal structure construction.
Tertiary phosphine chalcogenides having an O, S, or Se donor atom are considerable interestin the various areas as coordination chemistry [16], chalcogen-transfer reactions [17], and organometallic chemistry [18]. These substances are useful as startingcompounds for catalysis [19] and metal chalcogenide NPs [20]. Also, the synthesis, characterization and crystalstructure of a lot of them have been investigated [21]. Phosphine chalcogenides containing N-H and P=E groupscan act as a ligand to provide distinct complexing [22] with therapeutic [23] properties as well as participate in non-covalent interactions as diverse types of hydrogen bonds. The characterization of intermolecular forces involving N-H and P=E groups can clarify their critical roles in various processes as interacting drug design [24]. On the other hand, density functional theory (DFT) is a complementary theoretical approach for the experimental methods nearly all fields of chemistry [25]. Understanding diverse intermolecular forces present in structure crystals of phosphoramidates and their metal complexes has been contributed by Gholivand et al.[10,26]. Recently, we investigated intermolecular interactions in a triorganotin (IV) cocrystal with a phosphoramide derivative both theoretically and experimentally [27]. In our previous studies, a tertiary phosphine chalcogenide with formula (N2C4H3)C(O)NHP(S)(C6H5)2(1) was synthesized [28]. It was found that there are few comprehensive studies about the role of the non-covalent interactions on the formation and stability of the crystal structures and diagnosis of the typical synthons of phosphine chalcogenides [29]. Hence, we determined to systematically study the various types of non-covalent forces inside the lattice and detect all the molecular discernment properties that lead to the supramolecular synthons and compare these findings with the theoretical results at the end. Subsequently, two other model compounds with formula (N2C4H3)C(O)NHP(E)(C6H5)2 (E = O (2) and Se (3)) were selected to obtain more knowledge into the nature of the P=E bond in phosphine chalcogenides, and the NBO and QTAIM analyses were carried out. The molecular electrostatic potential (MEP) and energy gap of HOMO-LUMO for the title compounds were calculated as well.
Experimental
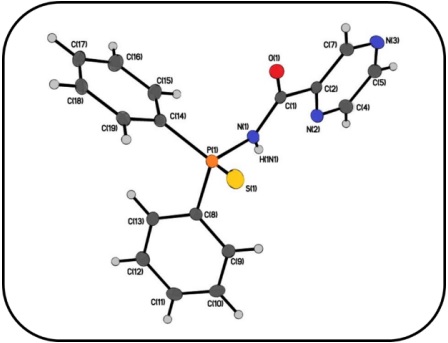
The structure of N-(diphenylphosphinothioyl)-2-pyrazinecarboxamide, (N2C4H3)C(O)NHP(S)(C6H5)2 (1), was taken from the ccdc database (Fig. 1)[28].
Computational details
The geometry of molecule 1 was optimized by Cam-B3LYP [30] method with 6-311+G* basis set and compared with the obtained experimental data. The optimized geometries are also confirmed by frequency analysis. To investigate the non-covalent interactions in solid-state structure, the X-ray structure of this compound was also applied as starting point for DFT studies in the gas phase. The crystal structure was modeled as dimers including two intermolecular-bonded phosphine chalcogenides. As X-ray crystallography cannot accurately determine the position of the H atoms, optimization of the H-atom positions was performed at the B3LYP/6-311G* level for the model clusters, while other atoms were kept frozen. The energies of intermolecular bonding were computed at the M062X/6-311G* level, based on ΔE between the dimer and its fragments, which are connected by the corresponding interaction as represented in the equation ΔE = ETotal − (EFrag1 + EFrag2), fragments 1 and 2 are two phosphine chalcogenide compounds 1. The contact energies have been corrected for the error owing to the superposition of the basis set (BSSE) through the counterpoise procedure method [31]. Moreover, two selected model molecules were optimized at the same level. By QTAIM [32] analysis at the Cam-B3LYP/6-311+G*, the electronic structure of substances was evaluated. NBO analysis [33] was carried out at the same level of theory. Quantum chemical studies were performed by the Gaussian 09 [34] in the gas phase. Besides, the non-covalent interaction (NCI) and the reduced density gradient (RDG) analyses [35] were performed to identify the intermolecular interactions observed in (N2C4H3)C(O)NHP(S)(C6H5)2 crystal structure at the M062X/6-311G* level using Multiwfn [36] and VMD 1.9.2 [37] programs. The value of sign (λ2)ρ exhibits the color of the isosurfaces. Hydrogen bonding, vander Waals, and non-bonded interactions are described through blue, green, and red color codes. The Hirshfeld surface analysis was performed by Crystal Explorer 3.1 program [38]. The intermolecular interactions in the crystal structure are located by the normalized contact distance map, d norm , and are quantified using the 2D fingerprint plots [39]. Further, DFT calculations have been carried out to predict EHOMO, ELUMO, and the electrostatic potential areas on the optimized geometry of all compounds at the Cam-B3LYP/6-311+G*.
Results and discussion
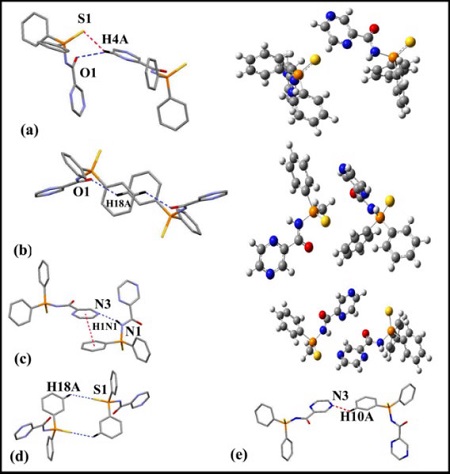
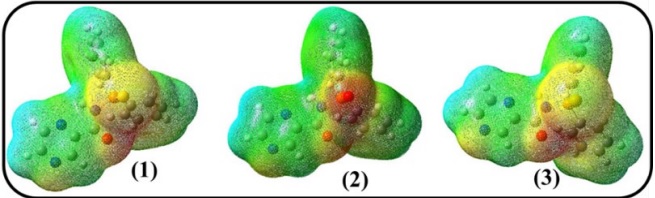
X-ray structure of (N2C4H3)C(O)NHP(S)(C6H5)2 (Fig. 1) was applied as starting point for theoretical studies and optimized by Cam-B3LYP/6-311+G* level. The selected crystallographic data [28] and the theoretical parameters are listed in Table S1. We have started by studying synthons 𝑅 1 2 (6), 𝑅 2 2 (12), and 𝑅 2 2 18 described in Fig. 2, which form through C−H…S and C−H…O interactions, as well as the self-assembled dimmers where different supramolecular interactions (C−H…π, C−H…N, N-H…N, and 𝜋…𝜋 stacking) are accountable for the fabrication of them and obtained these interaction energies. The studied dimers were obtained from the intermolecular interactions of the crystallographic structure of 1. Different non-covalent interactions will be discussed in light of NCI, Hirshfeld surface analyses, and the corresponding 2D fingerprint plots.
Non-covalent binding energies
Binding energies of supramolecular interactions in the crystal packing (ΔE) were calculated at the M062X method with 6-311G* basis set. We used a series of models to evaluate interactions on the basis of the reported method in papers [9,25]. First, the interaction energy of the complete assembly of each dimer was calculated. After, in this method, in order to estimate the contribution of an individual interaction, a neutral theoretical model has been used where the molecules of other interaction have been replaced or eliminated. Consequently, enrgy proportion of desired interaction would obtain. Fig. 2 shows the computational model used to study non-covalent interactions. Dimer 2a connects via C−H…S and C−H…O interactions to create 𝑅 1 2 (6) synthon. The interaction energy of the complete assembly was calculated, and its value was -4.80 kcal mol−1. To evaluate the share of both interactions (C−H…S and C−H…O), a model have been applied where the OC=O atom has been modified by a CH2 group (Fig. 2(a), right). The interaction energy is reduced to ΔE 2 = -3.00 kcal/mol for C−H…S interaction, and as a result the C−H…O interaction energy was calculated -1.80 kcal mol−1. A second model has also been utilized to measure C−H…O and C-H…𝜋 interactions in 𝑅 2 2 18 synthon (Fig. 2(b)). H-bond arising between a soft acid CH and a soft base 𝜋-system exhibits a fundamental role in a variety of chemical phenomena [40,41]. Based on the information provided, many organic structures showed short contact between 𝜋-system and C-H bonds [42]. The total assembly has considerable interaction energy (ΔE 1 = −13.59 kcal mol−1) that is diminished to ΔE 2 = −11.30 kcal mol−1 for two C−H…O bonds, when the phenyl ring has been changed using the methyl group (Fig. 2(b), right). The difference between both interaction energies (ΔE1−ΔE2) can be assigned to the contribution of both C-H…𝜋 contacts (nearly -1.147 kcal mol−1 for each C-H…𝜋 in agreement with distance; dH…Cg = 3.403 Å). Moreover, we have analyzed other self-assembly with N-H…N and 𝜋…𝜋 interactions between Pyrazine and Phenyl rings, respectively (Fig. 2(c)). A theoretical model has been used to determine the energy of each kind of non-covalent interaction. Therefore, hydrogen bond of N-H…N can be approximately estimated -8.25 kcal mol−1 (Fig. 2(c), right), and 𝜋…𝜋 interaction (dCg…Cg = -3.56 Å) roughly -3.83 kcal mol−1. Several researchers have documented the role of 𝜋…𝜋 stacking interactions in governing the structure of small compounds [14,43]. Finally, Fig. 2(d), e is shown 𝑅 2 2 12 synthon and the last self-assembly, where C-H…S and C-H…N interactions are formed between two neighboring molecules, respectively. The interaction energy obtained for these assemblies is ΔE = -1.80 kcal mol−1and -0.38 kcal mol−1.
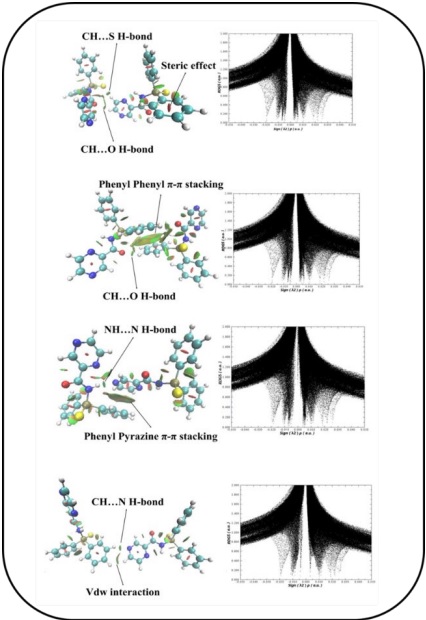
NCI approach
Recently, the NCI-RDG theoretical method has been applied better than the AIM technique to characterize van der Waals (vdW) interactions, repulsive steric interactions, and hydrogen bonds [44]. The NCI and the RDG S vs. (sign λ2)ρ plots are generated to investigate the existence of these interactions, where (sign λ2)ρ is the electron density multiplied by the sign of the second Hessian eigenvalue (λ2) (Fig. 3, right). The (sign λ2)ρ value is useful helps in anticipation interaction nature. (sign λ2)ρ < 0 correspond to attractive interaction like hydrogen bonds, whereas sign(λ2)ρ ≈ 0 and (signλ2)ρ>0 correlate to the weak vdW types, and non-bonded regions, respectively. In every dimer, the spikes at the zero region show van der Waals forces (-0.01 <sign(λ2)ρ < +0.01 a.u.). Several peaks at positive signs can related to the non-bonded interactions with ρ critical values of 0.017 and 0.025 a.u. due to the pyrazine and phenyl moieties. Besides, a broad spike of density at values between -0.02 and -0.01 a.u. is observed in RDG graph, which demonstrates C-H…S, C-H···N, C-H…O, and N-H…N interactions. Fig. 3, left, exhibits the 3D plots of π···π stacking and C-H···π interactions in crystal structure. The pill-shaped and flat isosurfaces shows the importance of these interactions which cause to stable crystal packing.
Hirshfeld surface analysis
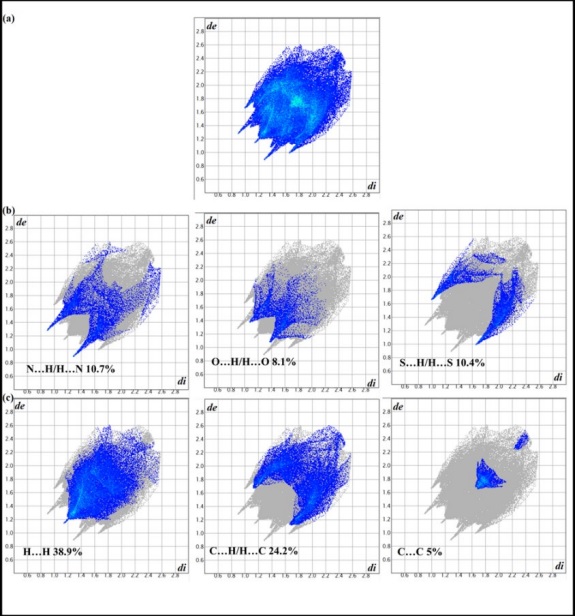
The Hirshfeld surface analysis was used to characterize the non-covalent interactions [45] in molecular structure of N-(diphenylphosphinothioyl)-2-pyrazinecarboxamide (1). The Hirshfeld surfaces (HS) mapped with shape index range of -1.0 to 1.0 Å, d norm range of -0.353 to 1.407 Å, the overall fingerprint plots (FPs) and the decomposed ones for the most significant contacts 2D fingerprint plots for 1 are shown in Figures 4 and 5. Pairs of blue and red triangles with bow tie pattern (on the surface mapped with shape index) observed in Fig. 4(a), are characteristic of π…π stacking interactions. On the Hirshfeld surfaces (d norm ) of 1, two deep red sites exhibit the intermolecular N…H-N interactions (labeled as 1 and 2 in Fig. 4(b)). Moreover, intermolecular C-H…S interactions are identified by light red areas near thiophenyl group and piprazine ring, labeled as 3 and 4 in Fig. 4(b). The C-H…S and C-H…O contacts are viewed as the pale red spots (labeled as 5 and 6). The decomposed FPs of the selected compound clarify the effect of the S…H, C…H, O…H, N…H, C…C, and H…H intermolecular interactions on the title molecular structures. Fig. 5 illustrates the contribution of all non-covalent intermolecular interactions in the selected crystal. The N…H-N hydrogen bond reveals two long sharp spikes on the 2D fingerprint plots of 1, containing 10.7 % of the total Hirshfeld surface area of substance (Fig. 5(b), left). The lower spike relates to the hydrogen bond donor (where d e <d i ), and the upper spike correlates with the H-bond acceptor (where d e >d i ), with d e +d i ~2.2 Å. The O…H-C and S…H-C interactions appear as shorter spikes in Fig. 5(b) (middle, right) with d e + d i ~2.5 Å and 2.68, respectively. The broadness of them may be corresponded to the presence of different O…H-C and S…H-C interactions. Further, H…H contacts view as a very distinguished spike on the diagonal of the plot in Fig. 5(c), left with d e + d i ~2.36Å and 38.9 % in 2D graphs. The share of C…H/H…C contacts corresponding to C-H…𝜋 interactions is the most significant interactions after H…H contacts (Fig. 5(c), middle). They have the value of de + di in molecule 1 (2.36 Å). 5 % of the total Hirshfeld surface area is related to the 𝜋⋯𝜋 stacking interaction which indicated as a small segment in (Fig. 5(c), right). A similar result was reported by Gholivand et al. in the case of the crystal structure of organotin (IV) with phosphoramides [46]. The lowest share of the total Hirshfeld surface in structure 1 is from H…O/H…O interactions at 8.1 %. All these interactions display the leading role in directing the crystal structure. [46,47].
Subsequently, we selected two model compounds with formula (N2C4H3)C(O)NHP(E)(OC6H5)2(E = O (2), Se (3)) and investigated the electronic structure and nature of P=E bond, which may be connected with electronic and steric effects, by DFT calculation, AIM, and NBO analyses. Although understanding the P=E bond features is key to optimizing their coordination to metalcations and their usein biological activities, a limited number of computational and experimental studies probe this issue.
Molecular electrostatic potential (MEP)
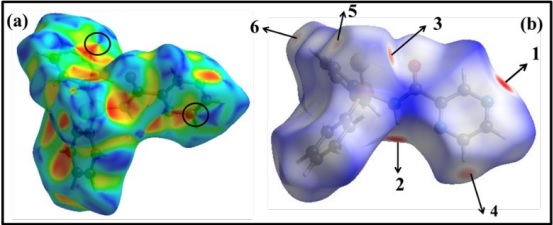
The electrostatic potential is broadly applied to characterize their activity, molecular stability and to distinguish the reactive sites of compound in nucleophilic/electrophili creactions and H-bonding interactions. Considering the overall molecular charge distribution, every area of the surface is demonstrated by different colors. Here, the blue and red maps display the electropositive and the electronegative potentials. The green exhibits the potential halfway between these two atmos [48].
In Fig. 6, the negative potential areas are enclosed over the chalcogenid atoms (S, O, and Se), OC=O, and NPyrazine. Thus, these sites are the most desirable areas for electrophilic attack in molecules. The appearance of the localized negative potential areas situated at the title regions is in agreement with the published experimental findings, which identified these areas as a reactive and coordinating part to the metal ions by coordination modes asmono, bridge, and bidentate ligand through Npyrazine, EP=E, and OC=O donor sites [49]. To explain this issue, the electronic features of the N=C and P=E bonds in these molecules will be investigated in the following sections.
QTAIM analysis
The values of electron density ρ(r), the electronic energy density H(r), and the Laplacian of the electron density ν2ρ(r) at the bond critical points (BCP) of P = E paths are presented in Table 2. The ∇2ρ values at the P = E BCPs are in ranging from -0.045 to 1.44 a.u and negative except that of phosphine chalcogenide 2, and the ρ values at the P = E BCPs are in the range of 0.135 - 0.232 au. Based on the calculated BCPs for P = E group (E = S and Se) in compounds 1 and 3 (H(r) < 0 and ∇2ρ< 0), the results show the strong interaction of P=S and P=Se bonds with the covalent bond property (Table 1). Further, the calculated charge density value at P=O BCP of 2 was determined to be 0.232 au, and the corresponding ∇2ρBCP value is positive, with amount to 1.44 au, which characteristic the principally closed-shell interactions [32, 50]. For compound containing P=O group, despite being positive ∇2ρ, H(r) is negative, and its value is -0.175 au, which indicates that this interaction is electrostatic with some covalent properties [51].
Table 1 Calculated QTAIM parameters (electron density, ρ, its Laplacian, ∇ 2 𝜌, and total electronic energy density, H(r)) at the critical point of P=E bond (E = S (1), O (2), and Se (3)).
| Compound | P=E | ||||
| ρ | IMAGEN | V(r) | G(r) | H(r) | |
| 1 | 0.172 | -0.298 | -0.1899 | 0.0577 | -0.132 |
| 2 | 0.232 | 1.439 | -0.7094 | 0.5346 | -0.175 |
| 3 | 0.136 | -0.046 | -0.1387 | 0.0636 | -0.075 |
Table 2 The values of ƩE (2) from lone pair (LP) of E ( = S, O, and Se) to P=X (X = N and C) antibonding (BD*) instudied compounds 1- 3 at Cam-B3LYP/6-311+G* levelof theory.
| Compound | Donor | Acceptor | IMAGEN | IMAGEN |
| 1 | LP (1) S 2 | BD* (1) P1 – N4 | 0.83 | |
| LP (3) S 2 | BD* (1) P1 – N4 | 27.35 | 28.18 | |
| LP (1) S 2 | BD* (1) P1 – C15 | 0.92 | ||
| LP (2) S 2 | BD* (1) P1 – C15 | 14.65 | ||
| LP (3) S 2 | BD* (1) P1 – C15 | 5.08 | 20.65 | |
| LP (1) S 2 | BD* (1) P1 – C26 | 1.01 | ||
| LP (2) S 2 | BD* (1) P1 – C26 | 15.24 | ||
| LP (3) S 2 | BD* (1) P1 – C26 | 3.47 | 19.72 | |
| 2 | LP (1) O 2 | BD* (1) P1 – N4 | 0.88 | |
| LP (3) O 2 | BD* (1) P1 – N4 | 29.65 | 30.53 | |
| LP (1) O 2 | BD* (1) P1 – C15 | 1.01 | ||
| LP (2) O 2 | BD* (1) P1 – C15 | 18.16 | ||
| LP (3) O 2 | BD* (1) P1 – C15 | 4.33 | 23.5 | |
| LP (1) O 2 | BD* (1) P1 – C26 | 1.14 | ||
| LP (2) O 2 | BD* (1) P1 – C26 | 18.67 | ||
| LP (3) O 2 | BD* (1) P1 – C26 | 2.80 | 22.61 | |
| 3 | LP (1) Se 2 | BD* (1) P1 – N4 | 0.87 | |
| LP (3) Se 2 | BD* (1) P1 – N4 | 25.14 | 26.01 | |
| LP (1) Se 2 | BD* (1) P1 – C15 | 0.95 | ||
| LP (2) Se 2 | BD* (1) P1 – C15 | 12.3 | ||
| LP (3) Se 2 | BD* (1) P1 – C15 | 4.32 | 17.57 | |
| LP (1) Se 2 | BD* (1) P1 – C26 | 1.02 | ||
| LP (2) Se 2 | BD* (1) P1 – C26 | 12.92 | ||
| LP (3) Se 2 | BD* (1) P1 – C26 | 2.87 | 16.81 | |
aThe values are reported in Kcal•mol-1.
NBO analysis
The natural hybrid orbitals (NHOs) of the P=E (E=O, S, Se) bonds in compounds 1 - 3 yielded the following composition: σPS=0.7090(sp2.37d0.02)P+0.7052(sp4.84d0.03)S, σPO =0.5179(sp2.15d0.05)P+0.8554(sp1.73)O, and σPSe=0.7398(sp2.45d0.02)P+0.6728(sp6.68d0.08)Se. Therefore, the phosphorus hybridization is between sp2 and sp3 in the studied compounds and the d-orbital share to P=E bonding is negligible. Analysis by second-order perturbation theory exhibited significant interactions between the P-Cipso and P-N antibonding orbitals and the electron lone pairs on the chalcogen atoms in derivatives 1 - 3 (Table 2). Here, each lone pair interacts with two P-Cipso and one P-N antibonding orbitals. More delocalization of the oxygen lone pairs lead tostronger interaction in 2. The same trend was observed for the stabilization energies of the reported phosphine chalcogenide [17]. This can be described by the stronger electron-withdrawing feature of the amido moietyas canbe viewed from the higher value of the polarization coefficient of the P atom in the NHOs presented above. Also, the NBO analysis exhibits that the LP E → 𝜎 ∗ (P−X;X=C, N) interaction among the subunits within compounds. The stabilization energies E 2 of LP E → 𝜎 ∗ (P−N) interaction are 28.18, 30.53, and 26.01 kcal/mol, and that of LP E → 𝜎 ∗ (P−C) interactions are 20.65, 19.72; 23.50, 22.61; 17.57, 16.81 in compounds 1-3, respectively (Table 2). This electronic delocalization causes the weakening of the P−X bond in order 2>1>3.
HOMO and LUMO
The energies of the lowest unoccupied molecular orbital (LUMO) and the highest occupied molecular orbital (HOMO) for derivatives 1-3 were computed by Cam-B3LYP method with 6-311G* basis set [52]. Fig. 7 display isodensity surface plot of HOMO and LUMO and the energy gap for these substances. As shown in Fig. 7, the LUMO electrons in all molecules are mainly delocalized on the pyrazine ring, C=O, and N-H moieties. For the phosphine chalcogenide 1, the HOMO electrons are delocalized over the phenyl rings, as well as, sulfide and oxygen atoms, while these electrons are delocalized over the phenyl rings and oxygen atom of carbonyl group for 2 and Se atom for 3 only. Molecule 2 with P═O group shows the highest energy gap and hardness with the calculated values of 7.51 and 0.138, respectively. And in contrast to 3 with the P═Se group, shows less energy gap and hardness than the other two chalcogenides (1 and 2). Using EHOMO and ELUMO, electron affinity (EA) and ionization potential (IP) can be also estimated as EA ~ -ELUMO, IP ~ -EHOMO [53]. The chemical softness (S) = 1/2ƞ [52] and chemical hardness (ƞ) = (IP- EA)/2 [54] values were calculated and were presented in Table 3. It is well known, softness (S) indicates the tendency of a molecule to react. According to the information in Table 3, hardness values determined for derivatives 1, 2, and 3 are 0.122, 0.138, and 0.113. Consequently, the hardness of material decreases with increase in the atomic size: Se>S>O. The trend observed is in agreement with the softness of the reported compounds [18a, 55].
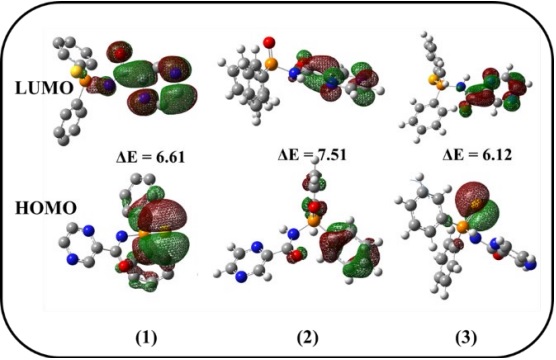
Fig. 7 Plots of the HOMO, LUMO orbitals and ΔE (the energy gap between HOMO and LUMO (eV)) of the compounds 1, 2, and 3.
Table 3 Quantum chemical descriptors for derivatives 1 - 3 at Cam-B3LYP/6-311+G* level.
| Compound | EHOMO | ELUMO | ΔE (ev) | ƞ = (EHOMO-ELUMO)/2 | S =1/ƞ |
| 1 | -0.282 | -0.039 | 6.61 | 0.122 | 8.23 |
| 2 | -0.314 | -0.038 | 7.51 | 0.138 | 7.25 |
| 3 | -0.264 | -0.039 | 6.12 | 0.113 | 8.89 |
Quantum chemical descriptors include energy of highest occupied and lowest unoccupied molecular orbital (E HOMO and E LUMO ), energy difference between the LUMO and HOMO (ΔE L-H ), chemical hardness (ƞ), and softness (S).
Conclusions
The presence of structure-directing interactions in packing crystal of (N2C4H3)C(O)NHP(S)(C6H5)2(1) have been investigated by NCI plot index, Hirshfeld surface, and finger plot analysis, as well as interaction energies were computed by theoretical calculation. A distinguishing character of the crystal structure in the monomeric substances is the fabrication of the dimeric motifs via H-bonding and interaction with aromatic clouds. N−H…N interaction can be identified as an effective interaction to detect the alignment of compounds in supramolecular assemblies. Go along with common hydrogen bonds, non-classical hydrogen bondings including C−H…S, C−H…O, C−H…N, and C-H…𝜋 further stabilize the packing structures so thatenergy of them is within a range of −0.38 (C−H…N) to −8.25 (N−H…N) kJ.mol−1. Pyrazine and phenyl rings have a main role in directing the supramolecular assembly of the studied phosphine chalcogenideusing establishing C-H…𝜋 and 𝜋⋯𝜋 interactions. Besides, the electronic structure and strength of other two model derivatives with P=E functional group (E = O (2) and Se (3)) were optimized and investigated. The QTAIM analysis demonstrates P=O bond with electrostatic feature and a small amount of covalent overlap compared to P=E (S, Se) bondings with the nature of covalent. Further, the HOMO-LUMO energy gap of the studied compounds shows the effect of E atomic size on molecular softness. The NBO analysis exhibits that the LP E → 𝜎 ∗ P−X;X=C, N electronic delocalization weakens the P-X bond in compounds 1- 3 in order 2>1>3.











 nueva página del texto (beta)
nueva página del texto (beta)