Introduction
The concerted nature and stereospecificity of the Diels-Alder cycloaddition reaction have been rationalized in terms of the Woodward-Hoffmann rules of conservation of orbital symmetry. [1-3] According to these rules, and to Frontier Molecular Orbital (FMO) theory, [4-7] the reaction takes place through the interaction of the HOMO of one of the reactants (usually the diene) and the LUMO of the other (usually the alkene or dienophile). The energy difference between these orbitals, which is in turn altered by the presence of substituents in both reactants, [8] can be taken as a parameter indicative of the magnitude of the energy barrier for the process, although other parameters have been proposed. [9-11]
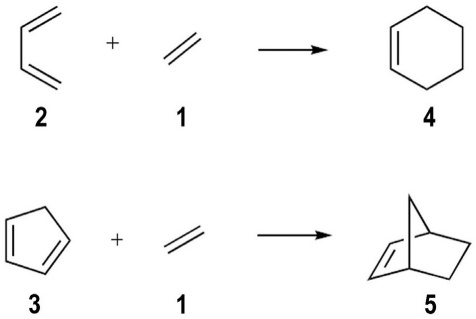
The cycloaddition of ethene (1) to 1,3-butadiene (2) is the simplest Diels-Alder reaction that can be carried out. The reactants contain the minimum number of atoms and double bonds required by the [4π s + 2π s ] process. The reaction between cyclopentadiene (3) and 1 (Scheme 1) can also be considered as a simple cycloaddition with two differences with respect to the former: (a) the diene is locked in the s-cis conformation required for the concerted reaction [12] and (b) the C5 methylene of 3 is a substituent that should alter the steric and electronic properties of the dienic π system. According to FMO theory, however, both reactions would be considered “neutral” in terms of the energy differences of the interacting orbitals of these essentially unperturbed systems. [13] Thus, the cycloadditions of 1 to 2 and 3 have relatively high activation barriers and are known to require high temperatures and pressures. [14-16]
A large number of experimental [15-23] and theoretical [10-11, 23-60] studies have been devoted to the analysis of these simple reactions, particularly to the study of the cycloaddition between 1 and 2. Nevertheless, herein we present a theoretical study of the intrinsic kinetics and thermodynamics of these reactions carried out at the SCS-MP2(FC)/aug-cc-pVTZ level of theory, with the goal of comparing the reaction coordinates and energy barriers of both reactions according to known energy partition schemes, and considering the role of dispersion in the interaction energy of the reactants, an issue that has not been addressed previously. Dispersion forces should be particularly important for these cycloadditions due to the non-polar nature of the reactants, and their contribution to the interaction energy along the reaction coordinate is expected to be brought out through the MP2 correlation energies. Because MP2 theory has been criticized on the grounds of its overestimation of the correlation energy, [61-62] we have carried out spin-component-scaled (SCS) MP2 calculations attempting to correct this deficiency. [63-67] An ever-growing number of reports suggest that this methodology yields more accurate interaction energies, even in complexes interacting through weak intermolecular forces. [68-74]
Theoretical methods
All the calculations described in this work were carried out at the SCS-MP2/aug-cc-pVTZ level of theory with the Gaussian 09 (G09) program package. [75] Geometries for the minima and transition states (TSs) were first obtained at the HF/6-31+G(d,p) level of theory and used as starting points for successive optimizations at the MP2/6-31+G(d,p), and SCS-MP2/aug-cc-pVTZ levels of theory. All SCS-MP2 calculations were carried out within the frozen-core approximation. The SCS-MP2 calculations were achieved by including the MP2 and IOp(3/125=0333312000) options of G09 in the corresponding input files, which applied Grimme’s original scaling factors [63] of 1/3 (truncated to 0.3333) and 6/5 to the second-order parallel (αα + ββ), and antiparallel (αβ) spin-pair contributions to the correlation energy, respectively. The TSs were located with the QST2 or QST3 G09 optimization options. Most stationary points were optimized within the C s point-group symmetry; for all of them vibrational frequency analyses were carried out after optimization. A single imaginary frequency was located for each TS; all frequencies were real for the minima. The electronic energies (E) of minima and TSs were corrected by the inclusion of zero-point energies (E 0); ZPE’s were obtained by applying a scaling factor of 0.9586 (determined for the SCS-MP2/aug-cc-pV(T+d)Z level of theory) to the vibrational frequencies. [76] The IRCs were determined from the corresponding transition states using the IRC G09 keyword. In each case the FORWARD and REVERSE sections of the IRCs were determined independently with a STEPSIZE of 30 (3.0 bohr/amu1/2); in all cases the USE=L115 G09 keyword was employed. Counterpoise corrections [77] for basis-set superposition errors were applied to all IRC points, including the adducts (see text); these corrections were determined with the COUNTERPOISE G09 keyword. Hartree-Fock, and MO energies were obtained from the G09 output files. The partition of the reaction coordinate energies into their deformation and interaction components was carried out as described below and extended to the analysis of molecular orbital interactions and to the partition of the interaction energy into the Hartree-Fock and SCS-MP2 correlation terms.
Deformation/Interaction energy partition scheme
For a bimolecular concerted reaction, the complex [Note 1] A*····B*, formed by the interaction of the reactants at any given point i along the reaction coordinate (Fig. 1), has an absolute electronic energy content that we will define as E (i) . In addition, this complex has a complexation energy ΔE (i) relative to the isolated reactants A and B, at their electronic and conformational ground states, energy that we will define at this moment in the standard way (eq 1):
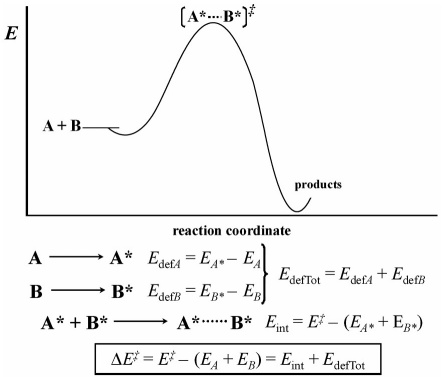
Fig. 1 Thermodynamic cycle employed for the decomposition of the complexation energy into interaction (E int) and deformation (E def) energies. The point of the reaction coordinate corresponding to the transition state ( ‡ ) is used as an example; however, this decomposition can be extended to any point along the reaction coordinate. A and B describe the geometries of the isolated reactants at their electronic and conformational ground states, while A* and B* correspond to the distorted geometries of the reactants at the point being considered.
where E A and E B are the electronic energies of the isolated reactants.
Within the deformation energy-interaction energy formalism we can define an interaction energy for the complex at each point of the reaction coordinate (E int (i) ), deformation energies for each one of the reactants, and a total deformation energy (E def A(i) , E def B(i) , and E def Tot(i) ) at these points.
The deformation energy corresponds to the energy increase arising from the change in geometry required by the isolated reactants (A and B) to reach the geometry they have within the complex (A* and B*), at any given point i of the reaction coordinate. Thus, if E A*(i) is the electronic energy of the distorted isolated reactant A* at point i, and similarly we define E B*(i) for reactant B*, we can write eqs 2-4.
The interaction energy at point i, E int(i) , is defined as the change in energy that takes place when the distorted isolated reactants A* and B* reach the geometry of the complex (A*····B*) at that point of the reaction coordinate (eq 5). According to the thermodynamic cycle, the sum of both E int (i) and E def Tot(i) terms should amount to the complexation energy at point i with respect to the isolated reactants (eq 6).
If the analysis is carried out with MP2 energies (E MP2), a further decomposition can be carried out considering that these energies correspond to the sum of the Hartree-Fock (E HF) and correlation E corr terms (eq 7).
As the MP2 calculation provides both, it is a simple matter to carry out the deformation/interaction energy partition considering each term independently.
Results and discussion
For the sake of brevity, from now on we will refer to the cycloaddition between ethene (1) and 1,3-butadiene (2) as the 1+2 cycloaddition and to the cycloaddition between ethene (1) and cyclopentadiene (3) as the 1+3 cycloaddition. To calibrate our methodology, we present in Table 1 the relative energies of the stationary points obtained in this work (reaction energies and energy barriers) with the SCS-MP2 methodologies, with and without the inclusion of counterpoise corrections.
Table 1 SCS-MP2/aug-cc-pVTZ relative energies a (kJ/mol) of the stationary points (SP) optimized in this work. b On the the right side of the table counterpoise-corrected (CC) values are presented.
| SP | ΔZPE | ΔE | ΔE 0 | ΔH | ΔG | cc | ΔE CC | ΔE 0 CC | ΔH CC | ΔG CC |
| TS 1+2 | 9.3 | 86.9 | 96.2 | 90.5 | 141.2 | 9.1 | 96.0 | 105.7 | 99.8 | 150.3 |
| TS 1+3 | 8.9 | 62.9 | 71.8 | 66.7 | 117.2 | 11.0 | 74.0 | 83.2 | 77.9 | 128.2 |
| 4 c | 27.7 | −191.5 | −163.9 | −172.2 | −114.6 | 18.6 | −173.0 | −144.1 | −152.5 | −96.0 |
| 5 | 24.3 | −130.4 | −106.0 | −113.6 | −58.1 | 20.3 | −110.1 | −84.7 | −92.4 | −37.9 |
a Relative to the isolated reactants at their most stable geometries; for 2 this corresponds to the s-trans conformer. b E: electronic energy, ZPE: zero-point energy, E 0: ZPE-corrected electronic energies, H: enthalpies at 298.15 K, G: Gibbs free energies at 298.15 K, cc: magnitude of the counterpoise correction and CC values. TS: transition state. c Corresponds to the half-chair conformer of cyclohexene.
From the table we can see that the energy barrier for the 1+2 cycloaddition is between 21.8 and 25.9 kJ/mol higher than that for the 1+3 reaction. The geometries of the transition states, in terms of the distance between reactants at the reacting centers, which is 2.243 Å for the former and 2.230 Å for the latter, are very similar for both reactions. However, the diene is more “parallel” to the dienophile in the 1+3 reaction, probably because of steric repulsion between the methylene of cyclopentadiene with the two syn hydrogens of ethene (Fig. 2). The reaction energies favor the formation of cyclohexene (4) much more than the formation of norbornene (5). In terms of the inclusion of vibrational energies relative to the isolated reactants, the effect is about the same for both transition states; for the products, the zero-point vibrational energy is higher for 4 by 3.5 kJ/mol. The magnitude of the counterpoise correction is modest for the transition states (~10 kJ/mol), and about twice as high for the products, in such a way that energy barriers and reaction energies become more positive with respect to the uncorrected values.
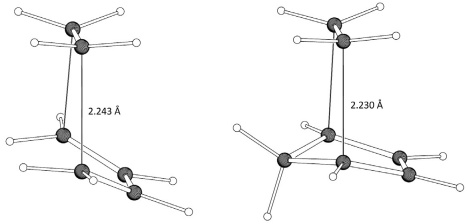
Fig. 2 SCS-MP2/aug-cc-pVTZ transition states for the concerted cycloadditions of ethene to 1,3-butadiene (left) and cyclopentadiene (right).
The reaction energies can be compared to those obtained from the experimental heats of formation of reactants and products which can be found in the NIST Chemistry Webbook. [78] From here we gathered the data for the heats of formation (Δ f H° g , kJ/mol) of: 1, 52.3; 2, 108.8; 3, 138.9; 4, −4.2; 5, 90.0. From these values the following gas-phase heats of reaction (kJ/mol) are calculated: Δ r H° g (1+2) = −165.3; Δ r H° g (1+3) = −101.3. We can see in Table 1 that the theoretical reaction enthalpy values (ΔH) with the inclusion of counterpoise corrections have a very good agreement with the thermochemical values. The experimental activation energies for these reactions have also been determined. For the 1+2 cycloaddition E a = 115.1 kJ/mol (~800 K); [17,19-20,22] while for the 1+3 process E a = 99.2 kJ/mol (~550 K). [16] From these values and the known relationship E a = ΔH ‡ − RT we can estimate ΔH ‡ = 108.5 kJ/mol (800 K) and ΔH ‡ = 94.6 kJ/mol (550 K). Again, we can see a better agreement with the counterpoise-corrected (CC) SCS-MP2 values of the corresponding transition states, considering temperature differences. Thus, at least for these two reactions, the inclusion of counterpoise corrections gives better results for both, ΔH ‡ and ΔH values, at least at the level of theory we used. [79] In Table 1we also included the ΔG ‡ and ΔG values for the 1+2 and 1+3 reactions, which are about 50-55 kJ/mol higher than the corresponding enthalpies and lead to very similar activation and reaction entropies (ΔS ‡ and ΔS) for all cases (~ −175 J/K∙mol).
In view of the above results, we decided to carry out the theoretical analysis of the energetics of these processes using the CC SCS-MP2 data. The IRCs for these reactions are shown in Fig. 3 as a function of the distance between the two reacting fragments (“bond-length” of the forming C-C bonds), considering that the symmetry point group of the reacting complexes along most of the IRCs is C s . In both cases the energies are relative to those of the isolated reactants at their lowest-energy geometries; for 1,3-butadiene this corresponds to the s-trans conformer.
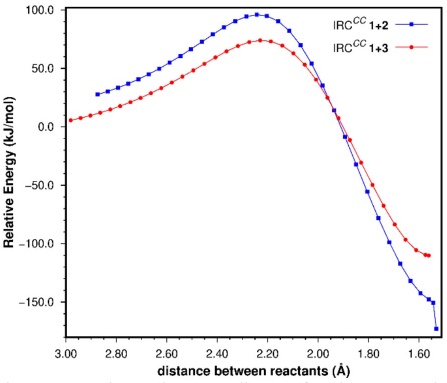
Fig. 3 SCS-MP2 counterpoise-corrected reaction coordinates for the 1+2 and 1+3 cycloadditions. For the former the last point on the right corresponds to the half-chair conformer of cyclohexene (see text).
There are several features worth noting. The IRC for the 1+2 cycloaddition runs a few kJ/mol higher than that for the 1+3 process up to a point beyond the TS. From there on, the former IRC goes down in energy more rapidly, leading to a product that is more stable (relative to the corresponding reactants) than the strained bicyclic norbornene, product of the 1+3 cycloaddition. We should not forget that the 1+2 cycloaddition takes place through the C s geometry of the reactants along the reaction coordinate which leads, in the first place, to cyclohexene in the boat conformation. However, the boat is a conformation with an energy higher than the two half-chair conformers. Thus, the last two IRC points for the 1+2 cycloaddition correspond to the boat and half-chair conformations, respectively; no IRC was determined for the conversion to the half-chair.
With respect to the intrinsic kinetics of these reactions, the relative difference in energy barriers between both reactions (22.0 kJ/mol) was analyzed in terms of the decomposition of the energy contents of the reacting complexes into their deformation (E defTot) and interaction components (E int) up to the TSs (Fig. 4), according to the distortion/interaction model, [80-87] also known as the Activation Strain Model. [87-93] Although this methodology has been used mainly for the comparison between isomeric transition states, it allowed us to make a direct comparison between the reaction coordinates of our two related reactions. The values obtained from this analysis at the TS geometries are presented in Table 2.
Table 2 SCS-MP2/aug-cc-pVTZ deformation and interaction energies (kJ/mol) of the TSs of the reactions under study. a
| SP | ΔE ‡CC | E def 1 | E def diene | E defTot | E int CC | E HF CC | E corr CC |
| TS 1+2 | 96.0 | 30.3 | 76.9 | 107.2 | −11.2 | 59.6 | −70.8 |
| TS 1+3 | 74.0 | 27.1 | 60.5 | 87.6 | −13.6 | 60.9 | −74.5 |
| Δ b | 22.0 | 3.2 | 16.4 | 19.6 | 2.4 | −1.3 | 3.7 |
a SP: Stationary point, ΔE ‡CC : CC electronic activation energy, E def 1: Deformation energy of ethene, E def diene: deformation energy of 2 or 3, E defTot: Total deformation energy of the reactants, E int CC : CC interaction energy, E HF CC : CC Hartree-Fock component of E int CC , E corr CC : CC correlation component of E int. b Difference between the 1+2 and 1+3 energy values.
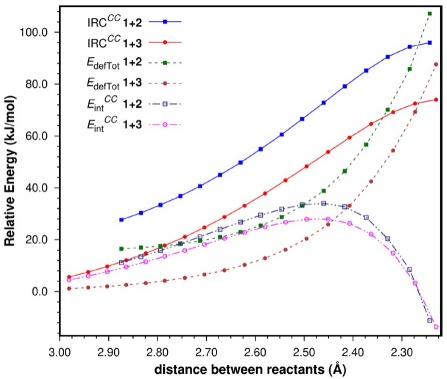
Fig. 4 CC SCS-MP2 deformation and interaction components of the IRC energy (kJ/mol) for the 1+2 and 1+3 reactions. The last points on the right correspond to the TSs.
It is readily seen that the major component of the differences along the first stage of both reaction coordinates is E defTot (ΔE defTot =19.6 kJ/mol at the TSs favoring the 1+3 cycloaddition). Very early on the study of cycloaddition reactions the issue of the s-trans conformational preference of 1,3-butadiene, and its effect on their rates was analyzed by a number of authors. [94-96] In particular, Eisler and Wassermann concluded that the conformational change of 2 from the more stable s-trans conformation to the s-cis geometry required for the reaction to take place, is the main reason why the activation energies of the cycloadditions of 2 are higher than those of 3 with the same dienophiles. [94,95] Thus, the E defTot term is more destabilizing for the 1+2 process as a result of the conformational change required of 2 for the reaction to take place; note that the difference is even higher at the beginning of the reaction. E defTot was further decomposed into the contributions of the individual reactants (e.g. E defTot(1+2) = E def(1) + E def(2)), as can be seen in Fig. 5.
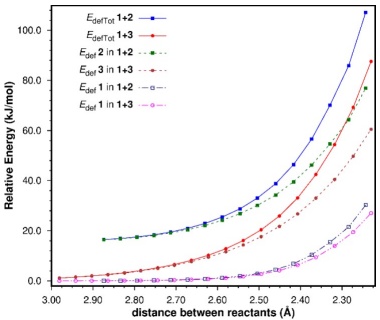
Fig. 5 Total deformation energies E defTot and individual deformation (E def) energies for each reactant (kJ/mol) in the 1+2 and 1+3 cycloadditions. The last points on the right correspond to the TSs.
In both reactions, the major component of E defTot is the deformation energy of the dienes. Again, the conformational change of 1,3-butadiene alone accounts for most of E defTot (see Table 2), [Note 2] although at the TSs, ethene is slightly more distorted in the 1+2 cycloaddition than it is in the 1+3 process, despite the fact that in the latter TS the contact between the reactants is slightly tighter.
Regarding E int, Fig. 4 shows that for both reactions this term is repulsive along most of the first stage of the IRCs although it is more so for the 1+2 reaction. However, at the TS, where E int is becoming attractive, the difference between the two interaction energies is relatively small with respect to the relative difference in activation barriers (ΔΔE ‡CC , 22.0 kJ/mol); ΔE int CC = 2.4 kJ/mol [Note 3] (Table 2), thus being slightly more stabilizing for the 1+3 cycloaddition. The fact that E int is repulsive in most of this region of the reaction coordinates can be attributed to the neutrality (in terms of Electron Demand) of the reactants, and contrasts with the attractive values of E int determined by our research group in reactions that take place by Normal Electron Demand.
To gain further insight into the origin of ΔE int, we took a quick look at the energies of the six electrons involved in the cycloaddition. Fig. 6 presents the MO energies of the distorted, isolated reactants at the geometry corresponding to the first point of the IRC, as well as the MOs of the interacting complex for the 1+2 cycloaddition. According to the diagram, the main contributor to the HOMO of the 1+2 complex (ψ3) is the HOMO of 2 (π2). Similarly, the main contributors to the HOMO−1 (ψ2) and HOMO−2 (ψ1) orbitals of the complex are the HOMO of 1 (π) and the HOMO−1 of 2 (π1), respectively.
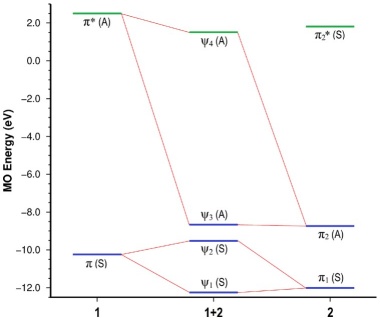
Fig. 6 MO perturbation diagram at first point of the IRC of the 1+2 cycloaddition showing the orbitals involved in the [4+2] interaction. Orbital symmetries are shown in parentheses. The orbital energies shown for the MOs of 1 and 2 correspond to those of the isolated reactants at the geometry of the reacting complex. Orbitals in blue are occupied, orbitals in green are unoccupied.
In Fig. 7 we present the MO energies of the orbitals shown in Fig. 6, along the reaction coordinates. [Note 4] From typical FMO arguments we could anticipate the 1+3 interaction to be stronger, because the electron-donor effect of the CH2 group of cyclopentadiene. Thus, the orbitals of 3 would be expected to be higher in energy than those of 2, giving rise to a stronger interaction with the LUMO of 1 (for the 1+2 cycloaddition, the strongest HOMO-LUMO interaction is HOMO(2)-LUMO(1) by 0.80 eV while for the 1+3 reaction the HOMO(3)-LUMO(1) interaction is even more favoured by 2.01 eV). Fig. 7(a) contains the MOs of the interacting complex, while Fig. 7(b) shows the MO energies of the relevant orbitals for the isolated reactants as they distort along the reaction coordinates; the effect of the C5 methylene of 3 can be clearly seen here. If we assume from Fig. 5 that the HOMO of 2 (or 3) becomes the HOMO of the complex, that the HOMO−1 of 2 (or 3) becomes the HOMO−2 of the complex, and that the HOMO of 1 becomes the HOMO−1 of the complex, we can relate the plot in Fig. 7(a) to that in Fig. 7(b). We can see that between the two reactions the largest differences in MO energies can be found in the HOMO−2 orbitals of the interacting complexes and in the HOMO−1 orbitals of the dienes. We can also see that deformation of the reactants causes small, continuous changes in the MO energies of the isolated reactants (Fig. 7(b)), being the HOMO−1 orbitals of the dienes the least affected.
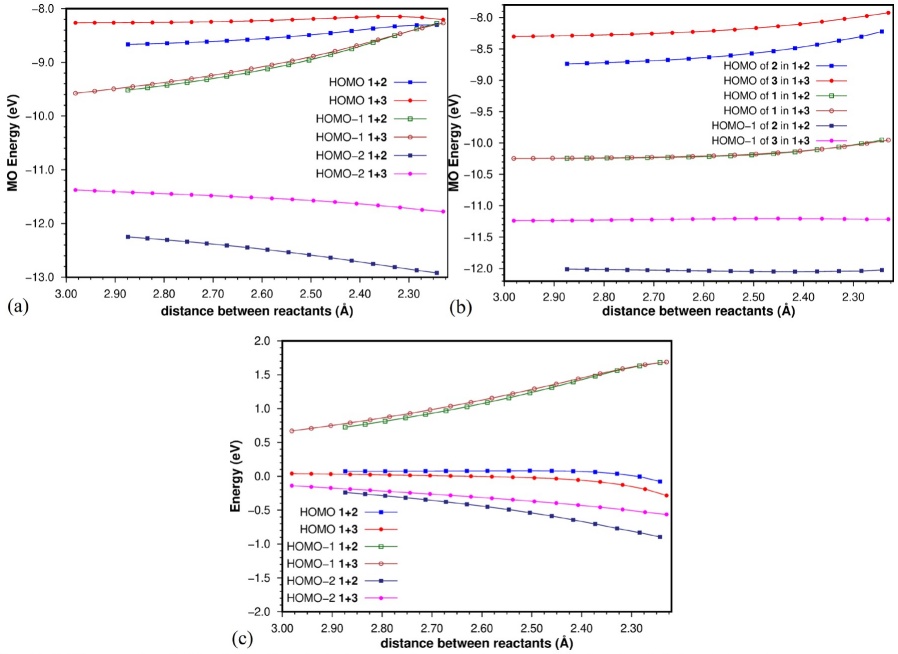
Fig. 7 MO energies (eV) along the first stage of the reaction coordinates for (a) the interacting complex and (b) the isolated reactants at the complex geometries. In (c) we present the subtraction of (b) from (a), which leaves only the effect of the interaction between reactants on the MO energies of the complex. The last points on the right correspond to the TSs.
As the MOs of the complexes contain both, deformation, and interaction effects, we subtracted the effect of deformation (subtraction of the data in Fig. 7(b) from that in Fig. 7(a)), at least of the MO that is the major contributor to the MOs of the complex. This exercise led to the results shown in Fig. 7(c), which essentially should display the effect of the interaction (perturbation) between reactants on the MO energy. We can see that the MO of the complex most affected by the interaction is the HOMO−1, which becomes more destabilized as the reaction proceeds. It is also interesting to note that the effect is about the same for both reactions, although this should not surprise us, as this orbital corresponds essentially to the perturbed HOMO of ethene. The other two orbitals of the complex, HOMO and HOMO−2 become slightly destabilized the former and slightly stabilized the latter for both reactions. However, the HOMO of the 1+3 reaction becomes less destabilized, and the HOMO−2 of the 1+2 reaction becomes more stabilized. According to the energy differences of these orbitals alone, if E int were composed only by the contributions of the MO interactions between the reactants (charge transfer effects), one would expect an overall stronger stabilizing interaction for the 1+2 reaction, which is not the case. Thus, it is not a good idea to assume that the energy changes of only these three orbitals will be the major contributors to the interaction energy between two reactants, when there are many other orbitals that are not considered in this analysis.
In a final attempt to explain the differences in E int CC between both reactions, we carried out a further partition of the SCS-MP2 interaction energies into their Hartree-Fock (HF) and correlation (corr) components; the results of this exercise are shown in Fig. 8 and in Table 2.
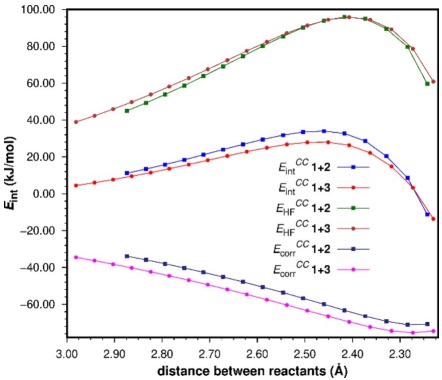
Fig. 8 Partition of the CC SCS-MP2 interaction energy (E int) into its Hartree-Fock (HF) and correlation (corr) components.
We can see that the HF components are quite a bit repulsive along the first stage of both reaction coordinates, although they are very similar for both reactions. At the transition states the difference between both HF components is only 1.3 kJ/mol, suggesting that for both reactions the HF contribution to E int is about the same; however, it is slightly less repulsive for the 1+2 reaction. On the other hand, the correlation components tell us a different story: first, they are rather stabilizing; second, there is a clear difference between the correlation terms of both reactions along the first part of the reaction coordinate. At the TSs the difference in the E corr CC terms amounts to 3.7 kJ/mol favoring the 1+3 process, thus representing the main contribution to the more stabilizing E int CC of the 1+3 TS with respect to that of the 1+2 cycloaddition. [Note 5]
As the HF component of the interaction energy corresponds to energy terms such as electrostatic interactions, charge transfer, exchange, and polarization, [97,98] Fig. 8 suggests that all these terms contribute to a similar extent in both reactions. On the other hand, the MP2 correlation term essentially corresponds to the effects of dispersion. In our interacting complexes this translates primarily into differences in the effect of van der Waals/London interactions between the reactants. The results we obtained suggest that the 1+3 TS is more stabilized because of the larger contact surface between these reactants due to the additional molecular surface of the CH2 moiety in cyclopentadiene. This can be better rationalized by looking again at the TSs in Fig. 2. The C5 methylene in 3 gives rise to a nonbonding interaction with the exo hydrogens of 1. The repulsion between these atoms causes the C2/C3 atoms of 3 to come closer to the endo hydrogens of 1 than the C2/C3 atoms of 2, thus creating a larger contact surface between the reactants.
Conclusions
The more stabilizing reaction energy for the 1+2 reaction can be attributed to the formation of a product (4) with less strain with respect to that obtained in the 1+3 reaction (5). The higher energy barrier for the 1+2 cycloaddition with respect to the 1+3 process (22 kJ/mol) is mostly due to the deformation that the reactants (19.6 kJ/mol), particularly 1,3-butadiene, must suffer for the cycloaddition to take place; in other words, to the mandatory adoption of the s-cis geometry of 1,3-butadiene. Only a fraction (2.4 kJ/mol) of the total difference in energy barriers between both reactions can be attributed to differences in the interaction energies between reactants at the corresponding transition states (Table 2).
Although a qualitative MO perturbation analysis supports the idea that the C5 methylene of 3 would lead to a better orbital interaction between reactants in the 1+3 cycloaddition, by increasing the energy of the π MOs of the diene, our overall results indicate that this is not relevant in terms of the interaction energies. A further partition of the SCS-MP2 interaction energies into their Hartree-Fock and correlation components indicates that electronic effects (which should be accounted for by the HF component), including MO perturbations, play a minor role in the differences observed in the systems under study. The ΔE HF CC term favors the 1+2 cycloaddition by 1.3 kJ/mol, while the ΔE corr CC term favors the 1+3 cycloaddition by 3.7 kJ/mol. This difference suggests that dispersion is the most important factor determining the overall difference in interaction energies. Thus, we conclude that for the 1+3 reaction dispersion interactions between reactants are stronger because of the larger surface area of 3. This agrees with other results obtained by our research group and supports the idea that the contact surface between reactants at the TS can play a significant role in determining the height of reaction barriers.
Notes
Note 1. In this particular case we will define "complex" as any geometry involving the interaction between both reactants, regardless of its position along the reaction coordinate.
Note 2. Note that at the level of theory employed in our work, for the planar s-cis conformation (which is not a minimum) ΔE0 = 14.7 kJ/mol with respect to the s-trans conformer.
Note 3. A similar trend is observed when uncorrected energies are used for the analysis.
Note 4. A simpler analysis of these MOs was carried out in Ref. 28 for the 1+2 reaction.
Note 5. Similar results are obtained when no CC corrections are applied.











 nueva página del texto (beta)
nueva página del texto (beta)