1. Introducción
Cada día la tecnología adquiere mayor relevancia tanto en la vida cotidiana como en los procesos educativos, siendo los programas informáticos cada vez más accesibles y necesarios. En el ámbito del aprendizaje de las matemáticas, el uso de aplicaciones tecnológicas contribuye al desarrollo del pensamiento creativo y a la resolución de problemas mediante el razonamiento matemático (Pilli y Aksu, 2013). En este contexto, GeoGebra se presenta como un software matemático gratuito que facilita el aprendizaje exploratorio. Su uso es intuitivo para principiantes y ofrece un entorno amigable tanto para estudiantes como para docentes (Dikovic, 2009). Una de las principales ventajas de GeoGebra es su capacidad para integrar geometría y álgebra en el proceso de enseñanza (Hohenwarter y Jones, 2007).
Considerando que la tecnología influye en los estilos de aprendizaje, su implementación, junto con la simulación y visualización de modelos matemáticos (Xistouri y Pitta-Pantazi, 2013; Akcay, 2017), puede transformar la comunicación abstracta entre profesores y estudiantes en una experiencia rica y accesible (Abramovich, 2013). En este sentido, el dominio tecnológico es una competencia esencial para la generación actual, y su fomento debería ser prioridad en las aulas de matemáticas (Mainali y Key, 2012).
En la educación universitaria, los estudiantes enfrentan dificultades al pasar de cálculo con una variable a varias. Existen investigaciones y propuestas didácticas que abordan estos desafíos (García-Oliveros et al., 2020; Prior Martínez y Torregosa Gironés, 2020), destacando problemas como la comprensión de gráficos multidimensionales (Pereira, 2020), simetría en representaciones de ternas (Agbolade et al., 2020), y la noción de espacio y dimensión. En el cálculo diferencial, el estudio de áreas irregulares y sólidos de revolución exige la integración de múltiples inteligencias, por lo que esta investigación se centra en el desarrollo del pensamiento matemático y espacial.
La geometría, en particular, requiere la orientación del docente y una complementación entre los enfoques sintético y analítico por parte del estudiante (Aroca Araújo, 2019). El uso de GeoGebra en el cálculo asistido por computadora rompe con los paradigmas tradicionales de la relación docente-estudiante, facilitando un aprendizaje más significativo (Coto Jiménez, 2020; Espinoza Guzmán et al., 2018). En este estudio de caso se analizó el impacto del uso de GeoGebra en el desarrollo del pensamiento matemático y espacial de los estudiantes. El aporte más relevante de la investigación es su contribución a la mejora de la calidad educativa tanto para la comunidad estudiantil como para la docente (Campos Soto et al., 2020).
Los estudios revisados subrayan la importancia del uso de GeoGebra en la enseñanza de la geometría, sugiriendo la necesidad de desarrollar una didáctica específica para su implementación. El problema central radica en cómo mejorar la enseñanza de la geometría y el aprendizaje de las matemáticas en el nivel universitario, utilizando GeoGebra como una herramienta eficaz (Morales Chicana et al., 2022).
A partir de este marco, se plantea la siguiente pregunta de investigación: ¿cuál es el impacto del uso de GeoGebra en la enseñanza y aprendizaje del cálculo diferencial e integral en estudiantes de Cálculo I en la educación superior universitaria? El objetivo general es determinar dicho impacto, y se derivan los siguientes objetivos específicos: a) evaluar el impacto de GeoGebra en las dimensiones del pensamiento matemático, tales como autorregulación, metacognición, significatividad, percepción del entorno, lenguaje simbólico, modelación de procesos, comunicación efectiva y lógica; b) comparar las habilidades de pensamiento matemático y espacial entre los estudiantes que aprenden con y sin GeoGebra; c) identificar cuál es la dimensión del pensamiento matemático que más influye en la mejora de las habilidades de pensamiento matemático y espacial.
2. Materiales y métodos
El pensamiento matemático se caracteriza por su dinamismo, claridad, progreso y simplicidad, desempeñando un rol fundamental en el aprendizaje (Reyes-Santander et al., 2018). Según Blossier y Richard (2014), este tipo de pensamiento está estrechamente relacionado con el uso de herramientas informáticas y el desarrollo de habilidades específicas en la interacción con dichas herramientas. Basándonos en esta premisa, se considera que el pensamiento matemático y espacial deben reforzar los conocimientos adquiridos en matemáticas. Para este estudio, se diseñaron encuestas centradas en las dimensiones del pensamiento matemático propuestas por Ocaña Gómez et al. (2019). Estas encuestas abarcaron ocho dimensiones y veinte subdimensiones, utilizando una escala Likert de 1 a 10, donde 1 representa el valor más bajo y 10 el más alto (ver Tabla I).
Tabla 1 Estructura del cuestionario con escala de Likert antes y después de la enseñanza del GeoGebra
| Dimensión (sección) | Subdimensión | Ítems | Escala |
|---|---|---|---|
| Autorregulación | Habilidad, comportamiento, desarrollo social y cognitivo | 01, 02, 03, 04, 05, 06, 07, 08 | Likert |
| Metacognición | Operaciones intelectuales, asociación al conocimiento, aprendizaje significativo. | 9,10,11 | Likert |
| Significatividad | Nivel de uso del GeoGebra | 12, 13 | Likert |
| Percepción del entorno | Modelación de sus cálculos en herramientas digitales, comprensión entre los modelos | 14 | Likert |
| Lenguaje simbólico | Conoce operadores lógicos, estratifica resultados, toma decisiones acertadas | 15 | Likert |
| Modelación de procesos | Software GeoGebra | 16 | Likert |
| Comunicación efectiva | Socializa el conocimiento, reconoce habilidades y debilidades | 17 | Likert |
| Razonamiento | Argumentación, trascendencia, origen de modelos matemáticos | 18, 19, 20 | Likert |
Fuente: Datos de la prueba piloto
Las encuestas fueron aplicadas a estudiantes de Cálculo I en la Universidad Nacional de San Cristóbal de Huamanga, seleccionados en función de su experiencia en el área de matemáticas. Los estudiantes autorregularon su conocimiento, lo que aportó validez a la investigación, ya que se procesaron los datos a partir de sus propias apreciaciones (Romero-López et al., 2020).
La metodología adoptada fue de enfoque cuantitativo, con un diseño cuasi experimental de nivel explicativo. Se implementaron pretest y postest para evaluar el impacto del uso de GeoGebra en la enseñanza del cálculo diferencial e integral (Arias, 2012). Los estudiantes fueron previamente informados sobre los objetivos de aprendizaje, los criterios y los procedimientos de evaluación (Alsina et al., 2019). La muestra estuvo compuesta por 60 estudiantes universitarios de ciencias e ingeniería, distribuidos en dos grupos independientes: un grupo control y un grupo experimental. La selección de los estudiantes fue inclusiva para aquellos que asistieron regularmente y aprobaron, excluyéndose a los estudiantes que no asistieron y los que no estaban matriculados. El muestreo se realizó mediante una técnica probabilística de tipo aleatorio estratificado.
3. Resultados
En esta sección se presentan los datos que respaldan la calidad científica de la investigación a nivel metodológico. Se trata de un estudio de tipo aplicado, con un nivel explicativo y un enfoque inductivo-analítico. El diseño utilizado fue pre-experimental, con la aplicación de pretest y postest tanto al grupo de control, que siguió un método de enseñanza tradicional, como al grupo experimental, que utilizó GeoGebra. Ambos grupos contaron con el mismo número de participantes.
Una vez recolectada la puntuación de cada estudiante, se procede a validar ¿qué?, aplicando un análisis de correlación canónica y una prueba de Kolmogorov-Smirnov, para determinar si se rechaza o no la hipótesis nula de la investigación (Freire et al., 2020).
3.1 Propuesta de modelos de trabajo
Se diseñaron cuatro propuestas de trabajo matemático siguiendo el programa de contenidos en matemática de la Universidad Nacional de San Cristóbal de Huamanga ([UNSCH], 2018), específicamente se abordó el tema de funciones reales de variable real por ser el más extenso y de mayor aplicación en los distintos programas de formación.
Las actividades de aprendizaje que establece el programa de matemáticas de la universidad son:
Números reales.
Valor absoluto.
Desigualdades.
Distancias entre la recta real.
Intervalos y entornos.
Resolución e interpretación gráfica de ecuaciones e inecuaciones
Utilización de las herramientas algebraicas en la resolución de problemas.
Medida de un ángulo en radianes. Razones trigonométricas de un ángulo.
Uso de fórmulas y transformaciones trigonométricas en la resolución de triángulos y problemas geométricos diversos.
Vectores libres en el plano. Operaciones. Producto escalar. Módulo de un vector.
Ecuaciones de la recta. Posiciones relativas de rectas. Distancias y ángulos. Resolución de problemas. Idea de lugar geométrico en el plano.
Cónicas. Análisis.
Funciones reales de variable real: clasificación y características básicas de las funciones polinómicas, racionales sencillas, valor absoluto, parte entera, trigonométricas, exponenciales y logarítmicas. Raíces complejas en funciones cuadráticas: características, expresión y representación. Dominio, recorrido y extremos de una función. - Operaciones y composición de funciones. Aproximación al concepto de límite de una función, tendencia y continuidad. - Aproximación al concepto de derivada. Extremos relativos en un intervalo. Interpretación y análisis de funciones sencillas, expresadas de manera analítica o gráfica, que describan situaciones reales.
A continuación, se adaptaron al modelo de enseñanza en línea. Es importante resaltar que la didáctica del docente se rige por las teorías de enseñanza y aprendizaje de Van Hiele actualizadas (Wahab et al., 2017); las propuestas de trabajo son:
3.1.1. Propuesta 1
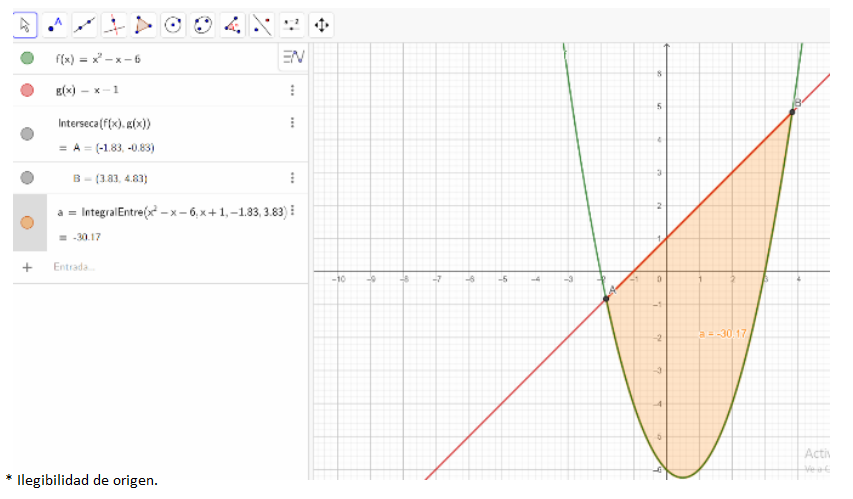
Estimación del área entre dos curvas para la función
En la primera propuesta, el docente orientó en el modelado a través del software asistido GeoGebra y los estudiantes presentaron evidencias de su desarrollo (Figura 1).
3.1.2. Propuesta 2
Estimación del área bajo la curva “La integral como límite del área” o “suma de Riemann”. Calcule la suma de Riemann para la para la función
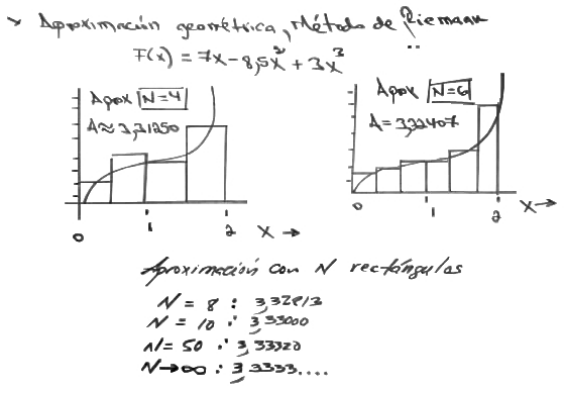
Figura 2 Memoria de cálculo de un estudiante seleccionado al azar, utilizando modelo de Riemann, para la función
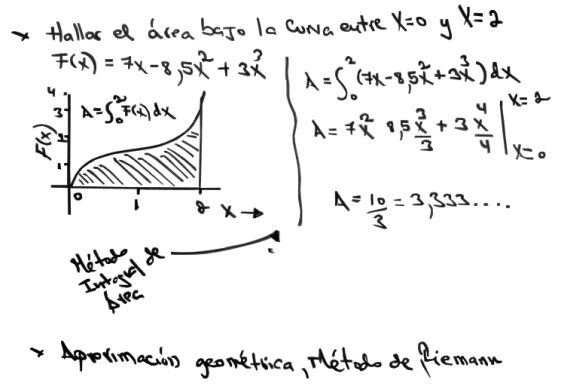
Figura 3 Memoria de cálculo de un estudiante seleccionado al azar, utilizando modelo de integral limite, para la función
En esta propuesta, se solicita a los estudiantes que elaboren una memoria de cálculo utilizando el método de Riemann por aproximaciones y la integral como límite de área. Esta memoria se comparará con el modelo simulado en GeoGebra para extraer conclusiones. Además del análisis descriptivo, se realizó un análisis estadístico para determinar si existen diferencias significativas en el uso de GeoGebra entre los estudiantes de Cálculo I (Vaillant et al., 2020).
3.1.3. Propuesta 3
Representar el sólido de revolución, punto a punto y estimar el volumen usando GeoGebra 3D, para la integral definida:
De la misma manera, siguiendo la instrucción docente se procedió a determinar el modelo propuesto para estimar el volumen del sólido de revolución (Figura 4).
3.1.4. Propuesta 4
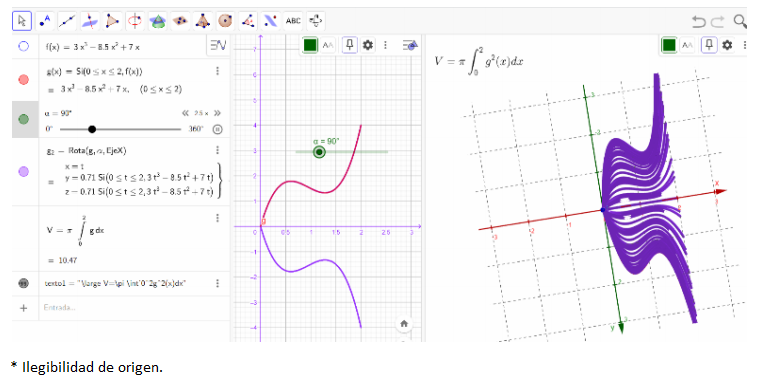
Representar las funciones
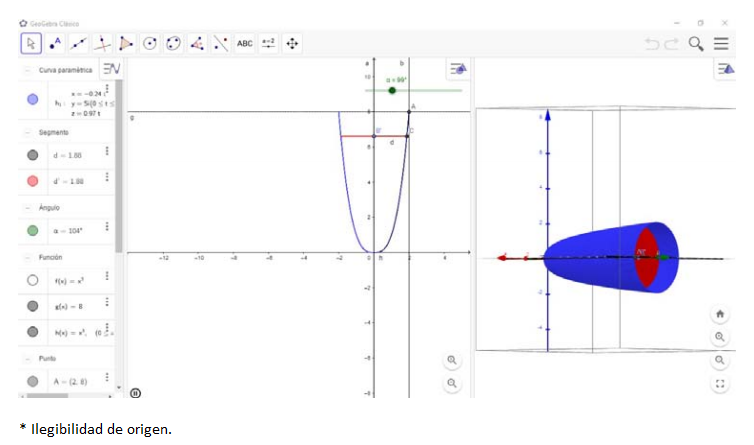
Figura 5 Solido de revolución de las funciones
Los estudiantes representaron su modelo geométrico utilizando el software, guiados por el docente según el modelo aplicado en estudios recientes de geometría. De acuerdo con Fabres Fernández (2016, p. 91), “una propuesta metodológica efectiva es aquella orientada a tareas de conceptualización, investigación y demostración, que fomente habilidades como visualización, dibujo, comunicación, razonamiento lógico y transferencia, basadas en los niveles de razonamiento propuestos por Van Hiele y un enfoque de resolución de problemas”.
3.2. Análisis estadístico
Para evaluar las mejoras en el pensamiento matemático y espacial, los datos recolectados de las encuestas realizadas antes y después de la aplicación de GeoGebra en la asignatura Cálculo I se analizaron mediante una correlación canónica. Este análisis permitió estudiar la relación entre los dos momentos de enseñanza-aprendizaje y determinar cuán vinculadas están las ocho dimensiones con la variable canónica, identificando correlaciones directas e inversas. El Análisis de Correspondencia Canónica (CCA) permite examinar la relación proporcional o inversa entre dos o más distribuciones (Restrepo-Betancur et al., 2019). Se realizó una prueba de permutación para verificar si la relación entre la tabla de contingencia y las variables explicativas es significativa. Los coeficientes de adecuación de las variables canónicas (U, V) son cruciales, ya que determinan qué dimensiones son significativas y permiten aceptar o rechazar la hipótesis nula (Vera, 2019):
Sean dos vectores aleatorios
Asimismo,
Tal que la correlación entre U y V sea máxima. Sean S XX y S YY las matrices de covarianzas de X e Y respectivamente y sea S XY la matriz de covarianzas de las variables de X y de Y. Si suponemos que las varianzas de U y V son igual a 1 entonces nuestro problema se traduce en encontrar los vectores a y b tal que maximizan a t S XY b que es la correlación entre U y V.
Si y sólo si,
En este sentido, las variables resultantes U y V se las llama variables canónicas solución, a los vectores a y b primeros vectores canónicos y a la
La prueba de Shapiro-Wilk se utilizó para evaluar la normalidad del conjunto de datos de los estudiantes de Cálculo I. Teóricamente, la hipótesis nula plantea que la muestra
donde,
Finalmente, se aplicó una prueba de Kolmogorov-Smirnov entre las medias de las dimensiones antes y después de modelar las propuestas de trabajo matemático con GeoGebra, para comparar el valor-p computado con el nivel de significación alpha, de esta manera podemos asumir cuál de las hipótesis soporta la investigación. Si “p” es mayor que “alpha” se acepta la hipótesis nula, en caso contrario se rechaza. Entonces, se contrasta la hipótesis de normalidad de la población, el estadístico de prueba es la máxima diferencia de:
siendo
4. Discusión de resultados
Los valores propios para el pensamiento matemático y espacial antes y después de usar GeoGebra indican que las variables canónicas necesarias para las correlaciones entre ellas es una sola, “F 1”. En este sentido se explica el 90.615 % de la variabilidad con la enseñanza asistida por GeoGebra (Tabla II).
Tabla II Valores propios de correlación antes y después de usar GeoGebra.
| F1 | F2 | |
|---|---|---|
| Valor propio | 0.072 | 0.007 |
| Variabilidad | 90.65 | 9.385 |
| % acumulado | 90.615 | 100.00 |
Fuente: SPSS V26
Con base en los resultados de la prueba de Shapiro-Wilk, con nivel de significancia del 0.05, se observa que solo una combinación lineal de las dimensiones autorregulación, metacognición, significatividad, percepción del entorno, lenguaje simbólico, modelación de procesos, comunicación efectiva, razonamiento (0.058) presenta la mayor correlación (ver Tabla III).
Tabla III Prueba de Lambda de Shapiro-Wilk
| Lambda | F | GL1 | GL2 | Pr > F |
|---|---|---|---|---|
| 0.921 | 0.058 | 64 | 260.2772964 | 1.000 |
| 0.993 | 0.007 | 49 | 232.8798687 | 1.000 |
Fuente: SPSS V26
Las correlaciones de las dos variables canónicas generadas, “F 1” y “F 2”, refleja igual que la tabla anterior, que solo una variable canónica (0.268), está fuertemente vinculada con las dimensiones de la investigación (ver Tabla IV).
Los coeficientes de redundancia de ambos grupos de variables canónicas revelan que las variables “Y 1”, que son las ocho dimensiones evaluadas antes de implementar GeoGebra, presentan mayor nivel de explicación para las variables “Y 2” (después de implementar (GeoGebra); en cambio al examinar los coeficientes de redundancia de la variable “Y 2”, tienen menor nivel de explicación para las variables “Y 1” (ver Tabla V). Esto quiere decir que las dimensiones autorregulación, metacognición, significatividad, percepción del entorno, lenguaje simbólico, modelación de procesos, comunicación efectiva y razonamiento después de implementar el software tienen una variabilidad grande (90.615 %).
Tabla V Coeficientes de redundancia
| Coeficiente de redundancia (Y1): | ||
| F1 | F2 | Suma |
| 0.018 | 0.001 | 0.020 |
| Coeficiente de redundancia (Y2): | ||
| F1 | F2 | Suma |
| 0.010 | 0.001 | 0.011 |
Fuente: SPSS V26
Estos son los resultados que definieron el estudio, los coeficientes canónicos estandarizados (ver Tabla VI). A partir de aquí se definieron las combinaciones lineales de cada una de las dos variables canónicas que resultaron ser significativas. La dimensión lenguaje simbólico después de aplicar GeoGebra mejoró (0.510a), sabiendo que antes del software era menor (-0.053a) implica que su correlación es proporcional inversa, esta dimensión está vinculada con la variable canónica.
Tabla VI Coeficientes canónicos estandarizados
| Coeficientes canónicos estandarizados antes de GeoGebra (Y1): | ||
| F1 | F2 | |
| Autorregulación | 0.489 | -0.004 |
| Metacognición | 0.000b | 0.313 |
| Significatividad | 0.048c | -0.062 |
| Percepción | 0.489 | -0.004 |
| Lenguaje simbólico | -0.053a | 0.036 |
| Modelación | 0.048 | -0.062 |
| Comunicación | 0.000 | 0.313 |
| Razonamiento | 0.106 | 0.706 |
| Coeficientes canónicos estandarizados después de GeoGebra (Y2): | ||
| F1 | F2 | |
| Autorregulación* | -1.215 | 1.367 |
| Metacognición* | 0.861b | -1.000 |
| Significatividad* | 0.510c | 0.194 |
| Percepción* | 0.134 | -0.171 |
| Lenguaje simbólico* | 0.510a | 0.194 |
| Modelación* | -0.042 | -0.004 |
| Comunicación* | -0.042 | -0.004 |
| Razonamiento* | -0.042 | -0.004 |
a,b,c,d dimensiones significativas de proporcionalidad directa, * dimensiones después de implementar GeoGebra
Fuente: SPSS V26
El resultado más importante de la investigación está en la dimensión metacognición, dado que era nula antes de implantar el software (0.000b) y después de aplicarlo mejoró (0.861b).
También mejoró la dimensión significatividad después de la aplicación (0.510c), que era casi nula antes (0.048c). Ese mismo comportamiento se obtuvo para la dimensión percepción, que pasó de (0.134d) a (0.489d); aunque hay una pobre correlación, es significativa. Sin embargo, las dimensiones de modelación, comunicación y razonamiento no experimentaron cambios significativos, lo que indica que no se correlacionan con el uso del software. Además, la dimensión de autorregulación no mostró mejora, mostrando una correlación inversa que indica una desmejora después de la implementación del software asistido.
En la Figura 6 se representan de forma gráfica los resultados de los coeficientes canónicos estandarizados, en el primer cuadrante se muestran las dimensiones metacognición*, percepción*, significatividad* y lenguaje simbólico* como las dimensiones más importantes del estudio. El mejor valor de adecuación en ambas variables lo muestra la variable canónica F1 con un valor de (0.254) en la Tabla VII.
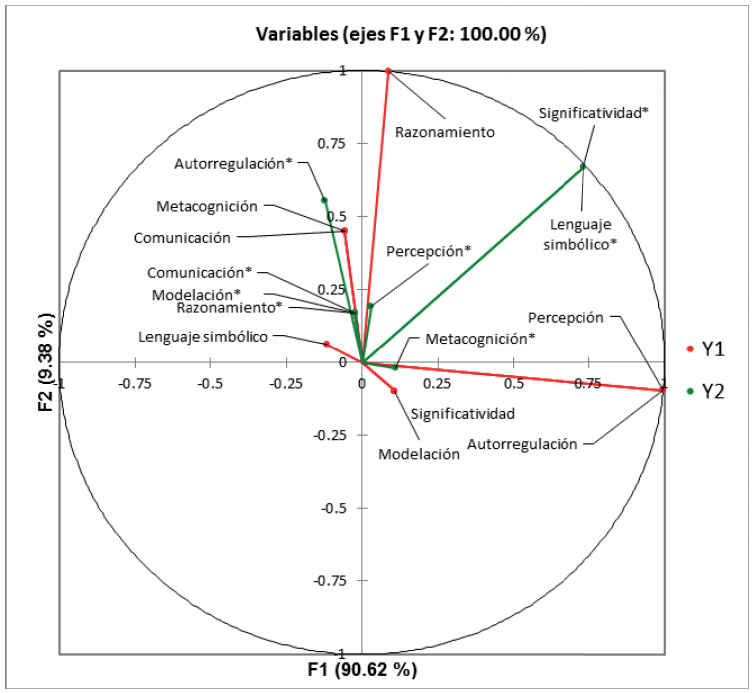
Figura 6 Gráfico de coeficientes canónicos estandarizados, en relación a las ocho dimensiones de estudio
Tabla VII Prueba de Kolmogorov-Smirnov para validez de distribución de la población
| D | 1 |
|---|---|
| Valor p-bilateral | Menor a 0.0001 |
| alfa | 0.05 |
Fuente: SPSS V26
Este es el resultado final la investigación, donde se muestran los coeficientes de adecuación del estudio, la variable canónica más representativa es (F 1=0.254) (Tabla VIII).
Tabla VIII Coeficientes de adecuación de las variables canónicas.
| Coeficientes de adecuación de las canónicas | |
| (Y1): F1 | F2 |
| 0.254 | 0.180 |
| Coeficientes de adecuación de las canónicas | |
| (Y2): F1 | F2 |
| 0.138 | 0.166 |
Fuente: SPSS V26
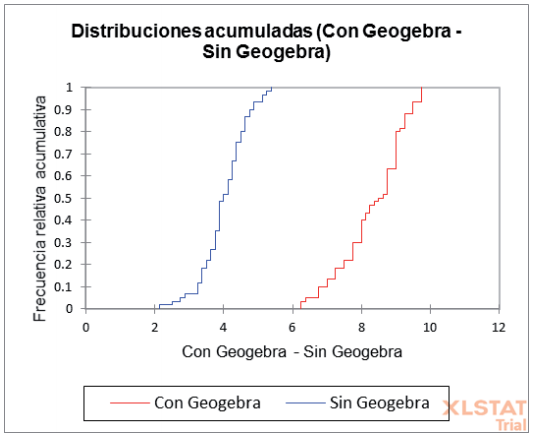
En la Figura 7 se muestra que los estudiantes otorgaron una puntuación más alta al estudio después de implementar GeoGebra en la asignatura Cálculo I. En las dos líneas de tendencia, las puntuaciones sin GeoGebra están entre 2 y 6 en promedio, mientras que en el segundo cuestionario el promedio está entre 6 y 10 en la escala de Likert, lo que representa que los estudiantes mejoraron sus habilidades de desarrollo del pensamiento matemático y espacial, corroborando con el estudio que las dimensiones que marcaron esta apreciación son metacognición*, percepción*, significatividad* y lenguaje simbólico*.
5. Conclusiones
Se concluye que el uso de GeoGebra tuvo un impacto significativo en la enseñanza y aprendizaje del Cálculo diferencial e integral en estudiantes de educación superior. GeoGebra demostró ser una herramienta eficaz tanto en la enseñanza general de las matemáticas como en la de Cálculo específico (Lemos y Almeida, 2019). La investigación evaluó el impacto del software en diversas dimensiones del pensamiento matemático: autorregulación, metacognición, significatividad, percepción del entorno, lenguaje simbólico, modelación de procesos, comunicación efectiva y razonamiento.
A diferencia del estudio de Vilchez-Quesada (2019), que se centra en la satisfacción estudiantil y rendimiento académico con el software VilCretas, la presente investigación profundiza en la relación entre variables canónicas antes y después de la implementación de GeoGebra, con un énfasis en habilidades cognitivas como la autorregulación y la metacognición. Se observó una alta variabilidad (90.615%) en las dimensiones tras la implementación del software.
La investigación también revela limitaciones del software educativo en ciertas dimensiones del aprendizaje, mientras que el estudio de Lugar Geométrico en GeoGebra se enfoca en aspectos visuales y conceptuales. Sería útil explorar cómo las visualizaciones geométricas pueden influir en dimensiones metacognitivas como la autorregulación y modelación (Gómez-Chacón y Escribano, 2014). Ambos estudios sugieren que el software educativo no es una solución universal, sino que su eficacia depende del enfoque y las dimensiones evaluadas.
Finalmente, se identificó que la dimensión metacognición es la más representativa en la mejora de habilidades matemáticas y espaciales, seguida de lenguaje simbólico, significatividad y percepción. Las dimensiones menos vinculadas a las variables canónicas fueron razonamiento, modelación, autorregulación y comunicación, sugiriendo la necesidad de investigar más en estas áreas.











 nueva página del texto (beta)
nueva página del texto (beta)