Introducción
Las escuelas son construcciones de la más alta importancia por la necesidad de proteger la vida de los alumnos y profesores. En particular, en zonas sísmicas resulta fundamental que el edificio escolar cuente con un nivel de seguridad razonable (ASCE, 2010; CENAPRED, 2001) y, dada la incertidumbre en este tipo de acciones, es indispensable un enfoque probabilístico que tome en cuenta las características aleatorias de las variables (De León, 2010). México es un país que en algunas de sus zonas tiene una alta exposición sísmica (Singh & Ordaz, 1994) por lo que sus estructuras requieren de una evaluación cuidadosa (Mendoza, 2013).
Se han propuesto distintos métodos para evaluar la seguridad sísmica de escuelas (Alcocer, 2021; Anelli et al., 2019) incluyendo los costos de las técnicas de reparación (Beigi et al., 2016; Chiu et al., 2013; Fung et al., 2021) y las incertidumbres de la acción sísmica (Cheng et al., 2018; De León & Ismael, 2019). Sin embargo, se cuenta con pocos procedimientos que consideren los costos de consecuencias de falla en el ciclo de vida de la escuela (Esteva et al., 2002; Esteva, 2021).
En México, el Instituto Nacional de la Infraestructura Física Educativa (INIFED, 2016), ha dado pasos concretos para contar con normas para reparar daños sísmicos en escuelas. De poco más de 2000 escuelas dañadas por los sismos de septiembre de 2017 en México, 200 tuvieron daños graves. Sin embargo, hacen falta procedimientos para garantizar que la reparación sea óptima para el resto de la vida útil de la escuela. En el presente trabajo se explora una formulación basada en la evaluación de riesgos y el costo mínimo esperado en el ciclo de vida (Ang & De León, 2005). La metodología propuesta incluye la valoración de los costos probables por daño considerando la posible ocurrencia de temblores en el resto de la vida útil de la escuela y considera los costos esperados de las consecuencias de falla, no solo el costo de reparación.
Estos costos probables se basan en las probabilidades de falla de la estructura para cada técnica de reparación empleada y la técnica óptima, por el lado de las alternativas planteadas, será la que involucre el menor de los costos totales esperados en el ciclo de vida. Así, una de las contribuciones del presente trabajo consiste en identificar el nivel óptimo de seguridad para proteger la escuela de los temblores posibles en el resto de su vida útil. Las guías y criterios actuales solo consideran que la reparación cumpla con los requisitos de un reglamento, lo cual lleva implícitamente a un nivel cercano al óptimo para el caso de escuelas en la Ciudad de México. Sin embargo, en otras zonas sísmicas del país los reglamentos (si existen y están actualizados) no llevan necesariamente a ese nivel óptimo. Otra aportación en la presente propuesta es la consideración explícita de costos de consecuencias de falla, lo cual no se realiza en la práctica ni está presente en los reglamentos de manera explícita, lo que conlleva a que la optimización no sea con base en el costo de reparación sino en el largo plazo. Se espera que en el futuro cercano, los reglamentos de los estados y municipios expuestos a peligro sísmico evolucionen hacia un código modelo donde los criterios que se apliquen involucren principios de costo/beneficio o riesgo/beneficio con optimización en el largo plazo. En la sesión siguiente se describe, con cierto detalle, la formulación propuesta.
Formulación propuesta
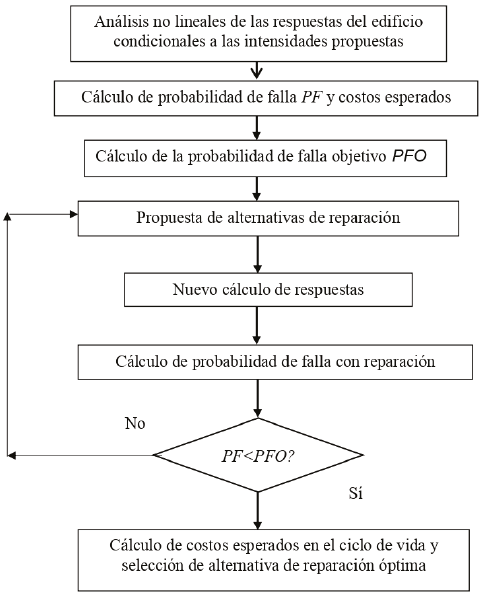
En la Figura 1 se presenta un diagrama simplificado que muestra a grandes rasgos el procedimiento propuesto. La primera parte consiste en establecer escenarios de intensidades sísmicas y evaluar las respuestas de la escuela ante estos escenarios de demanda sísmica, mediante análisis estáticos no lineales. Estas respuestas son condicionales a la ocurrencia de la demanda sísmica; con las probabilidades de falla condicionales y con las probabilidades de ocurrencia de dichas intensidades se completa la información para obtener las probabilidades incondicionales de falla, como se indica más adelante.
El cálculo de la probabilidad de falla involucra la aplicación del teorema de probabilidad total (Ang & Tang, 2007).
Donde la probabilidad de exceder el límite F condicional a la intensidad I es:
Donde A es la máxima acción para la intensidad sísmica I y 𝑅 es la resistencia. Las acciones y resistencias pueden ser acciones mecánicas o distorsiones de entrepiso. Imin e Imax son las intensidades mínima y máxima de interés, o sea, las que generan efectos importantes en la estructura. Con los análisis de la respuesta de la estructura se obtienen las demandas sísmicas que se emplean como los valores medios de las acciones. Las resistencias se calculan con procedimientos de la literatura (Bazán & Meli, 2001; Meli, 2008) y las especificaciones de normas vigentes (Gobierno de Oaxaca, 2020; Gobierno de la Ciudad de México, 2017). El coeficiente de variación de las acciones sísmica se toma 0.3 (Rosenblueth, 1986) y el de las resistencias 0.1 (Meli, 2008). Las probabilidades de falla se calculan haciendo uso de simulación de Monte Carlo (Ang & De León 2005). La probabilidad de falla objetivo PFO se calcula mediante la minimización del valor presente del costo esperado en el ciclo de vida.
El costo en el ciclo de vida (𝐿𝐶) se obtiene de sumar el costo inicial 𝐶𝑖n y el costo asociado a las consecuencias del daño/colapso CD (De León & Ismael, 2019):
Donde:
Crep = costo de reparación
𝐶con = pérdida de contenidos
𝐶susp = pérdida por suspender la operación del edificio durante el tiempo que tomen las reparaciones/reconstrucción
𝐶les = costo de las lesiones
𝐶𝑓at = costo de las fatalidades
El costo inicial se suele representar (García & De León, 2021):
Donde C1 es el costo de la estructura sin que hubiese sismo, y C2 es el costo de elevar la seguridad de la estructura en términos de reducir la probabilidad de falla en un ciclo de logaritmos naturales.
FVP es el factor de valor presente que se calcula como:
Donde:
δ = tasa neta anual de interés
V = vida útil de la escuela
Las pérdidas por lesiones o fatalidades se estiman a partir de trabajos previos (De León & Ismael, 2019; García & De León, 2021).
Otra etapa de la formulación es la de plantear las propuestas de alternativas de reparación, las cuales deberán tener similares niveles de seguridad. Para estas, la probabilidad de falla deberá estar ligeramente debajo de la probabilidad de falla objetivo. Existen muchas alternativas de reparación (INIFED, 2016) y en ellas se recomienda, en general, reparar los elementos estructurales dañados; sin embargo, en este trabajo la propuesta incluye reparar elementos dañados y reforzar otros que los análisis indiquen que se tienen que reforzar para reducir la probabilidad de falla de la escuela por debajo de la probabilidad de falla objetivo. En eso radica una de las contribuciones de la propuesta, pues se busca darle a la escuela un nivel de seguridad congruente con la probabilidad de falla objetivo para el resto de su vida útil. Por tanto, se requiere volver a calcular la probabilidad de falla y, mediante aproximaciones sucesivas, llegar a la estrategia de reparación que cumpla con esa condición. Así, las dimensiones de secciones y áreas de refuerzo comerciales que satisfacen esa condición representa la alternativa óptima para el nivel de exposición sísmica de la escuela considerada. En la sección que sigue se presenta el caso de estudio utilizado para ilustrar la formulación propuesta.
Caso de estudio
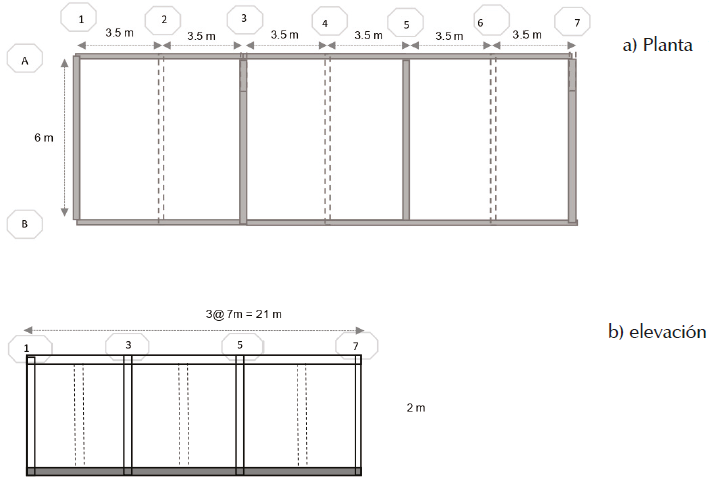
Se eligió una escuela en Juchitán, Oaxaca porque fue uno de los municipios más afectados por los sismos de 2017 (Sánches & Islas, 2017). Pese a ser una escuela pequeña (un nivel y 3 salones de 7m x 6 m), es un caso idóneo para ilustrar las ventajas del método propuesto. El sistema estructural está compuesto de marcos de concreto y muros de mampostería; las columnas tienen dimensiones de 0.20m × 0.40 m y las vigas de 0.25 m × 0.35 m. La planta y la elevación se muestran en la Figura 2.
Un ejemplo de los daños que tuvo la escuela en los sismos de 2017 fueron algunos agrietamientos en muros, como se muestra en la Figura 3.
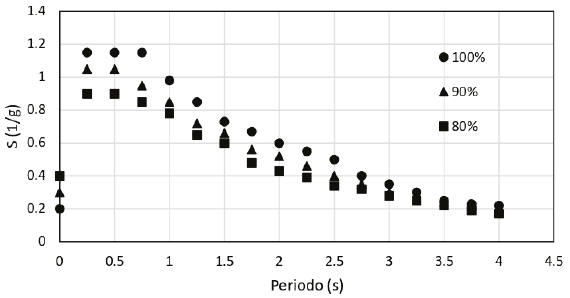
Se calcularon las respuestas de la estructura ante tres escenarios de intensidades sísmicas, el espectro original y dos más que se simularon por medio del escalamiento del espectro de peligro sísmico, a 90 y 80 % de las intensidades originales. Este espectro se obtuvo del Manual de Diseño de Obras Civiles para Diseño Sísmico, de la CFE (CFE, 2015; Hernández et al., 2016) (Figura 4).
Las respuestas máximas que son las que gobernaron el comportamiento son: Para columnas, la carga axial y el momento, para vigas, el momento. Se calcula el esfuerzo total combinado de flexión y compresión en las columnas y se observa que la componente de compresión es pequeña porque la estructura es de un solo piso. Asimismo, se obtienen los esfuerzos de flexión en vigas. Aquí, una hipótesis que simplifica los cálculos es que las propiedades geométricas iniciales (área y momento de inercia) son deterministas, lo cual es razonable debido a la poca variabilidad de las mismas (Bojórquez et al., 2017).
Se considera a las variables de respuesta y de resistencia, carga axial y momento, como variables aleatorias lognormales, los resultados de los análisis de respuesta sísmica se consideran como las medias de las acciones; las medias de las resistencias se obtienen del código para la Ciudad de México (De León & Ismael, 2021), y los coeficientes de variación Vr y Va de los esfuerzos resistente y actuante respectivamente, se obtienen de acuerdo con los procedimientos publicados en la literatura y normas vigentes y son: Vr=0.1 y Va =0.3. El índice de confiabilidad β se calcula por medio de simulaciones de Monte Carlo.
Como ejemplo, en la Tabla 1 se presenta una muestra para todas las columnas de los resultados obtenidos para la aceleración pico del terreno = 0.8 g. Se marcan en gris las columnas críticas.
Tabla 1: Media de los esfuerzos máximos y resistentes de las columnas, antes de la reparación, e índice β de confiabilidad para PGA = 0.8
| Columna | E(Sa) | E(Sr) | β |
|---|---|---|---|
| Kg/cm2 | Kg/cm2 | ||
| 1 | 36 | 143 | 5.84 |
| 2 | 38 | 143 | 5.56 |
| 3 | 61 | 143 | 2.86 |
| 4 | 67 | 143 | 2.75 |
| 5 | 37 | 143 | 5.57 |
| 6 | 39 | 143 | 5.49 |
| 7 | 42 | 143 | 5.01 |
| 8 | 44 | 143 | 4.87 |
| 9 | 48 | 143 | 4.45 |
| 10 | 46 | 143 | 4.66 |
| 11 | 52 | 143 | 3.98 |
| 12 | 49 | 114.58 | 4.05 |
| 13 | 59 | 114.58 | 3.02 |
| 14 | 57 | 114.58 | 3.07 |
De manera similar, las respuestas máximas en las vigas y sus índices de confiabilidad se muestran en la Tabla 2. De nuevo, el índice β se calculó con simulaciones de Monte Carlo (De León & otros, 2023). Se marcan en gris las vigas críticas.
Tabla 2: Media de las demandas y resistencias en términos de esfuerzos por flexión de las vigas, antes de la reparación e índice β de confiabilidad
| Viga | E(Sa) | E(Sr) | β |
|---|---|---|---|
| Kg/cm2 | Kg/cm2 | ||
| 1 | 32 | 150 | 4.83 |
| 2 | 44 | 150 | 4.03 |
| 3 | 51 | 150 | 3.78 |
| 4 | 59 | 150 | 3.25 |
| 5 | 67 | 150 | 2.70 |
| 6 | 69 | 150 | 2.67 |
| 7 | 38 | 150 | 4.30 |
| 8 | 32 | 150 | 4.83 |
| 9 | 44 | 150 | 4.03 |
| 10 | 51 | 150 | 3.78 |
| 11 | 64 | 150 | 2.80 |
| 12 | 33 | 150 | 4.82 |
| 13 | 43 | 150 | 4.04 |
| 14 | 50 | 150 | 3.79 |
| 15 | 65 | 150 | 2.79 |
| 16 | 30 | 150 | 4.84 |
| 17 | 42 | 150 | 4.05 |
| 18 | 56 | 150 | 3.74 |
Se calculó la probabilidad de falla de la escuela en condiciones originales (antes de la reparación) y resultó PF = 0.0028.
El paso siguiente consistió en aplicar las técnicas de reparación propuestas, la primera consiste en la adición de ángulos de acero A-36 en las esquinas de los miembros dañados: 2” X 2” X 1/8” en columnas y 1 ½” X 1 ½” X 1/8” en vigas (Figura 5). Este tipo de reparación representó un costo total de 32,000 pesos. Se calculó de nuevo la probabilidad de falla de la estructura reparada y se llegó a 0.0011.
La segunda técnica de reparación ensayada es la que consiste en la demolición del concreto dañado y la ampliación de la sección transversal de vigas y columnas, añadiendo el acero de refuerzo requerido (Figura 6). Las dimensiones de las secciones reparadas resultaron de 42 cm × 42 cm en columnas y 22 cm × 42 cm en vigas. Este tipo de reparación representó un costo total de 36,000 pesos. Se calculó de nuevo la probabilidad de falla de la estructura reparada y se llegó a 0.0012.
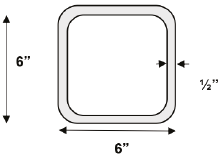
La tercera técnica de reparación consistió en la adición de contravientos tubulares de acero A-36 en las crujías dañadas (Figura 7). Este tipo de reparación representó un costo total de 135,000 pesos. Se calculó de nuevo la probabilidad de falla de la estructura reparada y se llegó a 0.0013.
Se calculó la probabilidad de falla objetivo para el caso de la escuela de Juchitán, aplicando datos específicos a las ecuaciones (4) a (7).
Además, se usaron C2 = 3 millones de pesos, δ = 10 %, V = 50 años FVP resulta 9.93. Para los costos de contenidos se tomaron costos comerciales de los muebles típicos en una escuela primaria, mesa bancos, escritorio, computadora, pizarrón, etcétera y para evaluar el costo de suspensión de actividades se consideró el precio de renta de un local similar en un sitio cercano a la escuela para seguir las actividades de enseñanza durante el tiempo de reparación, demolición y reconstrucción (García & De León, 2021). El costo de lesiones se estimó a partir de los costos de hospitalización y curaciones en centros de atención hospitalaria de la localidad. Y el costo de fatalidades se tomó de trabajos previos donde se calculó de acuerdo con la aproximación del capital humano (De León et al., 2023). Los datos y los resultados se muestran en la Tabla 3.
Tabla 3: Componentes de costo de falla (en pesos)
| Componente de costo | |
|---|---|
| Crep (altern. 1) | 32,000 |
| Ccon | 24,000 |
| Csusp | 22,000 |
| Cles | 150,000 |
| Cfat | 260 millones |
| CD | 260.25 millones |
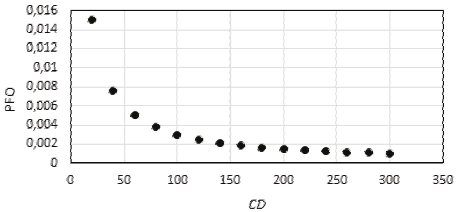
Se calcula la PFO para diversos valores de CD empleando las ecuaciones (6) y (7); el resultado se muestra en la Figura 8.
Se calcula el valor presente del costo esperado en el ciclo de vida para las tres alternativas de reparación y los resultados se muestran en la Tabla 4.
Tabla 4: Valor presente del costo esperado en el ciclo de vida (VPCECV) para las tres alternativas de reparación (en pesos)
| Alternativa | Costos esperados | VPCECV | |
|---|---|---|---|
| Directos | Indirectos | ||
| 1 | 32,000 | 46,000 | 78,000 |
| 2 | 36,000 | 38,000 | 74,000 |
| 3 | 135,000 | 71,000 | 206,000 |
Por lo que se infiere que la alternativa dos es la que implica el menor costo y es la que se elige de entre las tres alternativas de reparación. En la siguiente sección se discuten los resultados y sus implicaciones en la práctica.
Discusión de resultados
En el caso de estudio aquí tratado, referente a una escuela pequeña, la diferencia de costos totales (valor presente del costo esperado en el ciclo de vida) para las dos primeras alternativas de reparación es pequeña. En el caso de estructuras mayores la diferencia puede incrementarse, sobre todo si el daño se presenta más generalizado. Otro aspecto importante en cuanto a cuál alternativa de reparación puede tender a ser la óptima, se puede decir que no hay reglas generales, pero si los daños fueron muy localizados y hay una alternativa de reparación que corrige problemas locales (como fueron la 1 y 2 en este caso), esas tienden a ser las más efectivas. En cambio, si los daños son más generalizados y tienen que ver con todo el sistema estructural, una alternativa de reparación por contraventeo puede ser más eficiente que las otras, pues esta tiende a corregir deficiencias del sistema estructural global.
Debido al sistema estructural y a que la estructura era solo de un piso, las cargas axiales no rigieron, sino la flexocompresión en las columnas, con preponderancia de la flexión y la flexión en vigas. Las capacidades de los elementos se calcularon de acuerdo con la normativa vigente en el Estado de Oaxaca (Gobierno del estado de Oaxaca, 2020). En lo relativo a los impactos de las componentes de costo se encuentra el de fatalidades, debido a que se trataba de una escuela pública de educación primaria donde los niños cuentan con edades muy cortas, lo que produce que la vida útil remanente sea muy grande. Al calcular la pérdida por fatalidades con el criterio del capital humano, esta vida remanente genera que dicha pérdida por fatalidades sea alta. Además, en México las escuelas se clasifican con un nivel de importancia muy alta y se requiere tener un nivel de seguridad alto ante la exposición sísmica.
El alto nivel de peligro sísmico en la zona es otro factor de peso para tener un nivel alto de consecuencias de falla CD, lo que provoca que la probabilidad de falla objetivo tenga que ser baja. Otro tipo de estructuras y otro nivel de peligro sísmico podrían llevar a resultados diferentes.
El procedimiento propuesto tiene la versatilidad de tomar en cuenta el nivel de peligro, el nivel de importancia de la estructura, los modos de falla que gobiernan y las incertidumbres inherentes en el proceso, entre otros aspectos. La formulación propuesta toma en consideración la proyección de costos esperados en el ciclo de vida, no solo el costo de la reparación. Esto representa una valoración de costos en el largo plazo y una diferencia respecto a la práctica actual en donde solo se considera el costo de reparación. Por consiguiente, existe el beneficio a la sociedad de que se emplean los recursos de mejor manera, con optimización en el largo plazo.
El presente trabajo podría extenderse para considerar el multi-peligro en zonas del país donde su efecto es significativo, por ejemplo, sismo y viento. El modelo tendría que ampliarse para incorporar el peligro y la vulnerabilidad por viento en este caso. Y habría que generar envolventes de la probabilidad de falla en las alternativas de reparación para que cubran ambos peligros.
Este tipo de planteamientos, con aplicación a otros tipos estructurales, materiales y sitios con distintos niveles de peligro sísmico, pueden llevar a generar recomendaciones para actualizar las normas de diseño y reparación de escuelas.
Conclusiones
Se propuso un procedimiento basado en riesgo para elegir una alternativa de reparación de escuelas dañadas por sismo, entre varias opciones.
El procedimiento toma en cuenta el nivel de peligro sísmico del sitio, la importancia de la escuela y el nivel de daños producidos. Se incluyen las incertidumbres inherentes a demandas y capacidades y la proyección de comportamiento esperado en el largo plazo. Esta proyección considera, bajo ciertas hipótesis, el desempeño que la escuela puede tener en el resto de su vida útil.
Para el caso de estudio considerado, el costo más importante fue el de fatalidades, donde las alternativas de reparación propuestas fueron:
1) Adición de ángulos de acero en elementos dañados
2) Ensanchamiento de secciones de concreto con ajuste de refuerzo
3) Adición de contravientos tubulares de acero
Se mostró que, dependiendo del carácter local o global de los daños y los tipos de mejoramiento estructural que la estructura necesite, algunas alternativas de reparación pueden ser más eficientes que otras. Para la escuela estudiada, la alternativa dos fue suficiente y la que mejoró la seguridad de la estructura de manera óptima.
Se considera que una de las contribuciones del trabajo fue haber basado la selección de la alternativa de reparación no en el costo de reparación sino en el valor presente del costo esperado en el ciclo de vida, lo cual optimiza la selección de la alternativa de reparación en el largo plazo. La optimización en el largo plazo puede ayudar a mejorar la racionalización en el empleo de recursos para programas de reconstrucción por daños debidos a sismos.
Se debe tener precaución antes de tratar de aplicar estos resultados a problemas con características de peligro o de la estructura que sean distintas a las estudiadas aquí.
Algunas de las limitaciones del presente trabajo son que se analizó solo una estructura pequeña con sistema estructural sencillo, por lo que habría que extender el procedimiento para incluir otros sistemas estructurales, otros niveles de peligro, otros modos de falla, otras alternativas de reparación, etcétera.
En trabajos futuros habrá que incluir los aspectos anteriores y desarrollar otros procedimientos más detallados para calcular la probabilidad de falla de la estructura y para considerar el multi-peligro en sitios donde sea pertinente tomarlo en cuenta.











 nueva página del texto (beta)
nueva página del texto (beta)