1 Introduction
In one hand using computational power that yields on the Graphics Processing Units (GPU) cards with the aim to solve problems of general purpose [1, 2] is a topical issue. On the other hand, many bio-inspired algorithms, due to its own nature, can be parallelized as consequence of their population-based feature, see [3]. Some authors show that it is possible to achieve acceleration for parallelized bio-inspired population based algorithms just like Particle Swarm Optimization (PSO) algorithm when running inside a multi-threaded GPU [4, 5, 37], the parallel coding style used was the suggested in the C-CUDA programming tool [6]. In a previous work [3] we found that the best achievement could be reached when the complete set of experiments of the PSO algorithm was carried out by the GPU inspired by an parallel strategy called diffusion, which is already used in the field of parallel programming [7].
In their research, Cantú-Paz called embedded to the parallel execution they implemented because in the diffusion implementation there is only one processing entity per agent, while in the Cantú-Paz model they use one thread per agent (individual) instead of one processing entity per individual. Other bio-inspired algorithms like Differential Evolution (DE) [8], Evolutionary Computing [9], Ant Colony Optimization [10], and PSO [11] were implemented and tested as alternatives to find good results in hard-to-optimize problems getting good solutions in a satisfactory time. As long as these method work with a set of agents (individuals or particles), they trial several solutions at once supported on a set of rules and random procedure. These and another set of heuristic rules have been applied successfully a in most fields of human knowledge, generating acceptable results with good performance, running on all types of computer systems, including personal computers, see [12].
In this paper parallel versions of DE and PSO algorithms coded for GPU with multi-threading capacity are presented, the results obtained of DE and PSO these versions coded for parallel running are analyzed and compared as a new research activity of an earlier investigation [3]. The DE and PSO algorithms were selected since both of them are very popular and their general structure is practically the same. The computing power delivered by the GPU provides a processing speed increase, however, it also shows slightly different behavior from proposed parallel implementations, but with significant results compared to sequential implementations.
All of the above is a consequence of the GPU requirements to generate the random numbers needed to maintain diversity for the population-based heuristics.
The main contributions in this research are:
1) The alternative parallel implementation for both PSO and DE algorithms used.
2) The comparison of sequential and parallel implementations for both PSO and DE.
3) The random numbers generation offline approach used.
This paper is arranged as follows. Section 2 presents a short summary of related research. Section 3 shows a short description of the DE and PSO. Section 4 presents technical overviews of our parallel implementations. Section 5 informs the setup for the experiments and their results. In Section 6, we expose our opinions and conclusions.
2 Related Work
In many cases, parallel codification starts from a migration of a sequential programming code previously developed for sequential architectures and suitable for parallel or distributed architectures. In the case of population algorithms (such as Genetic Algorithms, Evolutionary Strategies, DE, Ant Colony Optimization, PSO, etc.), once their usefulness in sequential architectures had been demonstrated, attempts were made to use the computational power and its natural parallelism, as in the work of Roberge et al. [13] and Cantú-Paz [6].
In the previous works carried out in this area, the proposals based on traditional concurrent processes, which are executed in a single processing entity, can be highlighted, see [14]. However, in many other related works they are designed to work in heterogeneous architectures of several processors (like a Beowulf-type network or similar). One of the problems associated with this type of architecture lies in the communication overhead between different processing entities, a element that affects the performance of overall execution. Despite this, the parallelization of population-based algorithms is a common topic in research, as can be seen in recent research works that use parallel implementations using population-based bio-inspired heuristics to solve hard to optimize complex functions (see [15,3]).
Concerning the parallelization of population based algorithms in GPU, some of the first proposals were developed with Genetic Programming (GP), see [16]. More recently some research have been made by using Genetic Algorithm C- CUDA parallel programing using a GPU to crack Hash Function SHA-1, see [17]. In more recent times many population algorithms have been implemented in GPUs, see [36]. Regarding the CUDA language C, population algorithm implementations were carried out and one of the first was PSO, the authors took advantage of the advantages provided by an NVIDIA multi-threaded GPU. To carry out this work they used the CUDA programming tool in order to parallelize a PSO algorithm directly, see [3].
More recently Krause et al. [18] presented a DE algorithm programmed in C-CUDA and was one DE executed in a GPU, followed by more implementations, highlighting those by Fabris [19] and Casella [20]. In literature it is possible find works on comparing PSO vs. DE, but they are related to sequential implementations, like in [21, 22]. Youseff et al. have done a comparative study for DE vs PSO vs Scatter Search running on a GPU. There exists a development that uses both DE and PSO for model-based object detection, [23], but the comparison is made for a specific problem and is hard to compare against test functions commonly used. So authors acknowledge, there is no empirical study on comparing only DE vs. PSO running on a multithreading GPU for a set of test functions. This research shows an experimental study comparing parallel DE and PSO algorithms against their sequential variants running on a multi-threading GPU.
3 Overview of the Two Well-known Population-Based Algorithms
DE and PSO algorithms are both population-based algorithms that have proven their success in solving difficult optimization problems and are two of the most widely used bio-inspired algorithms for this kind of problems. Although their general constitution is similar (both have initialization, fitness evaluation, comparison and updating blocks), they use different rules for comparison and updating.
On one hand, the PSO algorithm is a collaborative strategy that finds a solution as a result of the movement of individuals that try to imitate the best individual of a neighborhood (local or global). On the other hand, when using Differential Evolution, individuals not only form teams of individuals to generate their offspring (using recombination and mutation operators) that actively try to enhance the better individual in the current population.
From the No Free Lunch Theorem [24], it is known that the success or failure of using a small set of well-performing reference functions does not ensure that an algorithm exhibits the same behavior for a different set of functions or for practical problems. Likewise, bio-inspired heuristics are also known to be aggressive on a set of problems. The goal of our research therefore is to supply a general description of the methodology that the GPU can use to decrease the convergence time according to the nature of the problem and its relationship with respect to the execution time and its dependence on the number of individuals or particles, as well as the number of iterations.
3.1. Particle Swarm Optimization Algorithm
From a study about the displacement of groups of birds that fly in a space of n dimensions and seek to solve, in a collaborative way, a problem with a global optimum, arise the Particle Swarm Optimization (PSO). At first, PSO algorithm was developed by Heberhart and Kennedy in 1995 [9], starting from the study of the position in the x-space and the variation of the v position(called velocity) for each particle.
In 1998, Shi and Heberhart [25] improved the algorithm, defined the concept of inertia (w), which improved the performance of the algorithm and increased its efficiency. Recent research has shown that the number of particles and their neighbors also modify the behavior of the algorithm, showing that the best value for a neighborhood is six particles [26].
To describe a PSO algorithm, pbx is defined as the better fitness found by the bird (particle) in a local individual search and gbx as the best global fitness of the entire population found so far, then a basic PSO algorithm in a global version is described as follows:
Finally, the velocity of each particle, in the PSO implementation, is bounded in a range [Vmin, Vmax ] in order to prevent exploding behavior.
3.2. Differential Evolution Algorithm
Differential Evolution (DE) appeared when in 1996 K. Price and R. Storm tried to fit parameters for Chebyshev polynomials [10]. There are different variations from original DE algorithm [27, 28, 29].
The DE variant that is most used is called DE/rand/1/bin, this is a Differential Evolution algorithm (DE) that generates his breed by using a random selection (rand), with one pair of difference vectors used (1), and a binary crossover scheme (bin). Basic DE/rand/1/bin algorithm works as follows:
We must highlight that, in order to obtain better results and with different types of problems, specific parameters for the problem and fixed parameters must be set up in the algorithm [30, 31].
4 Parallel Implementation with C-CUDA
As a starting point for the parallelization of population heuristics, the parallel categorization proposed for evolutionary algorithms in [32] was considered as a reference point, such as diffusion approach, migratory approach and global approach. In the work developed in [3], it should be noted that suitable way of the programming of parallel algorithms based on the population, in a GPU, is a so-called diffusion implementation.
In the broadcast scheme, there is a GPU thread for each individual, so that the calculation and evaluation of the fitness of a single individual is performed by a single GPU thread. For other part, comparisons between particles (individuals for DE) are accomplish inside the GPU following a thread synchronization process. This parallel variant is called Embedded by the authors, this is because almost all of the functional blocks are calculated within the GPU, only the initialization is done on the host. Therefore, the integrated approach was selected as the methodology coding basis for the parallel version of the PSO and DE heuristic algorithms on the Graphic processor card.
The DE and PSO heuristics described in Algorithms 1 and 2 will be implemented in a parallel programming using an encoding strategy that uses only one thread per individual and to execute code from a specific population algorithm it uses a kernel call. Therefore, inside the GPU all the particles are updated simultaneously, in the case of sequential code, the position update is carried out one particle after another, that is, particle by particle.
The functional blocks of the metaheuristic can be seen below:
— Initialization. Sets the initial random values of the particles that make up the initial population.
— Assessment of fitness function.
— Comparison. Find the fitness for all the particles and the select the best one in the population and compares it with the best registered one.
— Upgrade. Each particle updates its position according to the rules of the specific algorithm.
To explain the process of code parallelization, we have rearranged the sequential functional blocks, highlighting that the loops are in terms of the number of individuals. On the one hand, it must be taken into account that all function blocks run on host processor, for sequential implementation (see Fig. 1). On the other hand, only the initialization module is executed on the host processor for the case of our parallel implementation, called embedded (see Fig. 2), this is because the kernel call is associated with the optimization process, which includes: the comparison, fitness assessment, and upgrade modules, all run on the GPU using multiple threads (remembering it's one for each particle), waiting for a termination condition to be reached.
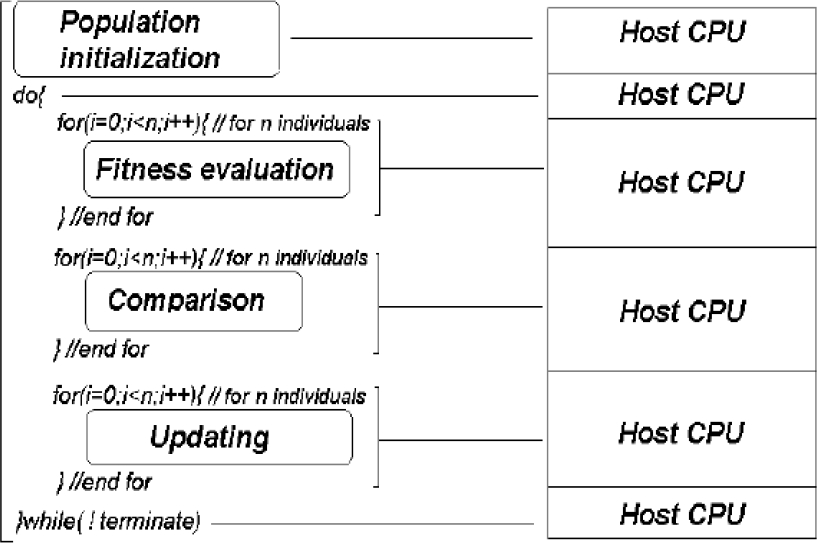
Fig. 1 General structure of both sequential PSO and sequential DE algorithms, for host-only execution
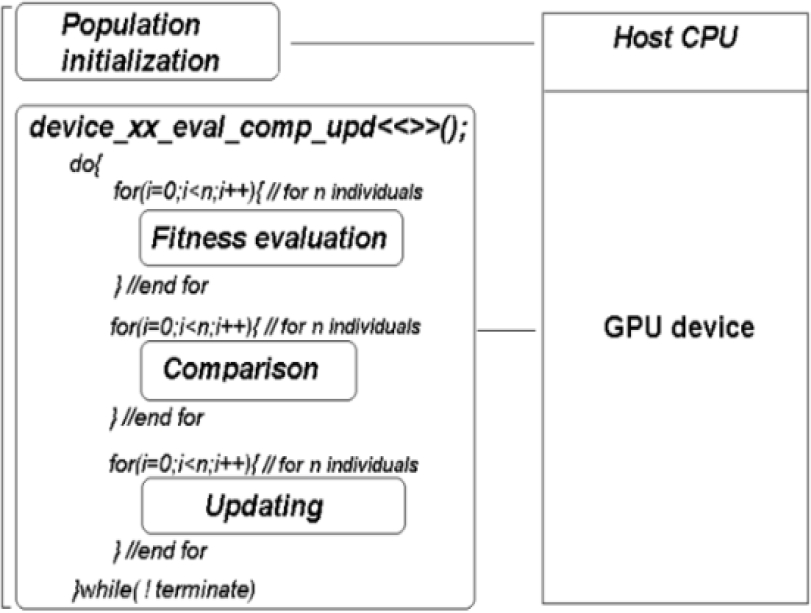
Fig. 2 The general structure of both sequential PSO and sequential DE algorithms, for host-GPU execution
As for the initialization module, the timer start seeds for the random numbers of the particle (one seed per thread), worked up on the host and remains as the only task executed outside the GPU. The precondition ensures diverse random number generation and good GPU fitness for each thread. This results in a different comportment o manner in relation to sequential algorithms, as shown in the experimental results. It should be noted that the generation of random numbers was carried out differently for parallel and sequential programming, this was due to the fact that the generation of random numbers presents a great difficulty inside the GPU from the same seed in the environment inside the GPU. The traditional way of generating random numbers (through the use of a single seed) was maintained for the case of sequential codes, while parallel codes used different seeds, one for each particle in the population, as will be described later.
The kernel call is made through the device_xxx_eval_comp_upd << >> () instruction, where xxx can be DE or PSO, depending on which algorithm was implemented, see fig. 2. For the functional implementation in coding a set of parallel population algorithms in the GPU, there is a set of practical considerations to take into account:
— Overhead. The GPU will experience the phenomenon of overload due to the waiting time (latency) in the memory transfers between the GPU device and the computer acting as host. Since transfers are comparatively slow, (relative to in-GPU computation) any parallel GPU implementation should minimize their use.
— Synchronization. Due to the very nature of population-based heuristic algorithms, individuals must share status information with each other, at least the best fitness, in our proposed parallel implementation the threads (i.e. individuals) have to communicate among themselves and a good synchronization is particularly important.
— Contention. When multiple threads simultaneously review global variables, a resource access problem is generated on the GPU, this is called contention. To face this problem, adequate precautions must be incorporated, in particular for the PSO and DE algorithms. In the case of population-based algorithms tested, contention occurs when an attempt is made to access the memory area corresponding to the index of the best global individual.
— Random number generation. As in all the stochastic process, you must be very careful since a problem can be generated when the random numbers must be generated within the GPU environment and the strategy for seed initialization is neglected. When calling a random number generation function like rand () to run on the GPU, you must ensure that numbers are generated for each call and for each thread. In case a set of different numbers is not guaranteed, it can cause the algorithm to have poor convergence or to be in fact non-convergent due to low diversity, since all the random numbers were generated identical for each particle.
5 Experiments
The system where the experiments were carried out is a personal computer using an Intel Core Duo processor with Fedora Linux OS (this in order to make the most equitable comparison with previous work, see [3]), this computing system is what we call host for this work. The graphics accelerator card installed in the host is an NVIDIA GeForce 8600GT GPU card with 4 multiprocessors, each of the multiprocessors consisting of 8 cores, representing a total of 32 processing cores and with 256 Mbytes of working memory. Each processing core was programmed using the environment that allowed writing parallel code for the GPU directly, the CUDA environment, since C-CUDA parallel calls were used, as described previously.
The purpose of the set of experiments that were carried out in order to be able to measure the performance of the DE algorithm in its parallel version and PSO, with respect to the sequential versions and between them. The experimentation consisted of the measurement For the set of functions with which the tests were performed, the functions were taken from a well-known reference set [30]. The calculation of the performance of the PSO and DE algorithms in their sequential and parallel versions was carried out by varying the iterations and the number of individuals while the optimization phase of the objective functions of each of the particles is carried out.
The selected test functions were carefully chosen. It can be seen that in the optimization of Function F01 PSO in its sequential form, it has a better convergence than the rest of the algorithms, followed by parallel DE, while sequential DE and parallel PSO algorithms they present an impoverishment in the results as the number of individuals increases. It is important to highlight the very different behavior of the parallel DE and PSO algorithms. In figure 10, it can be seen that during the optimization process of the F02 function, that the algorithm with the best convergence is the parallel DE algorithm, followed by the parallel PSO. n considering that they have a high optimization complexity for which four multimodal functions were chosen [33]:
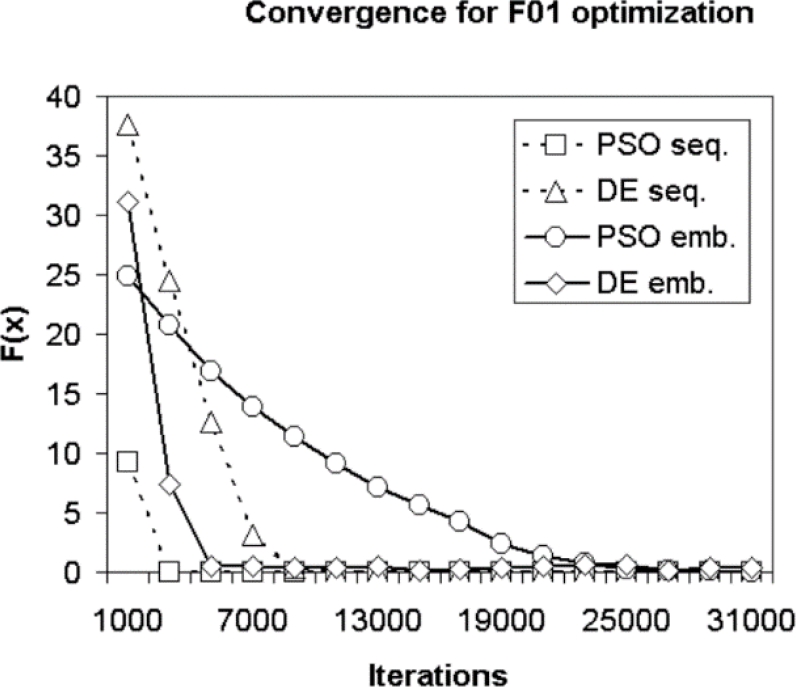
Fig. 3 Convergence for the F01 optimization setting variable number of iterations and the number of individuals fixed at 128
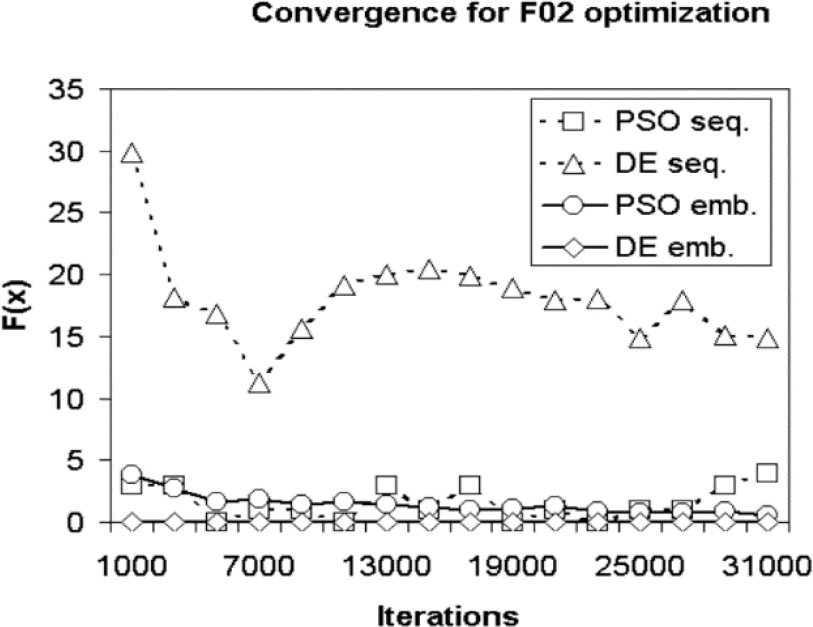
Fig. 4 For the function F02 with a variable number of iterations and with a number of 128 individuals we have the Convergence to the sequential one
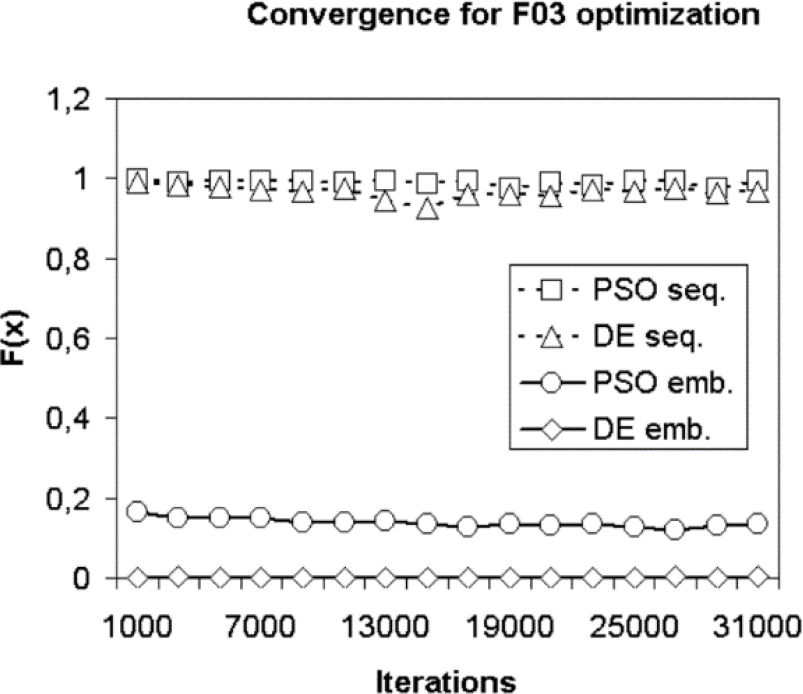
Fig. 5 For the function F03 with a variable number of iterations and with a number of 128 individuals
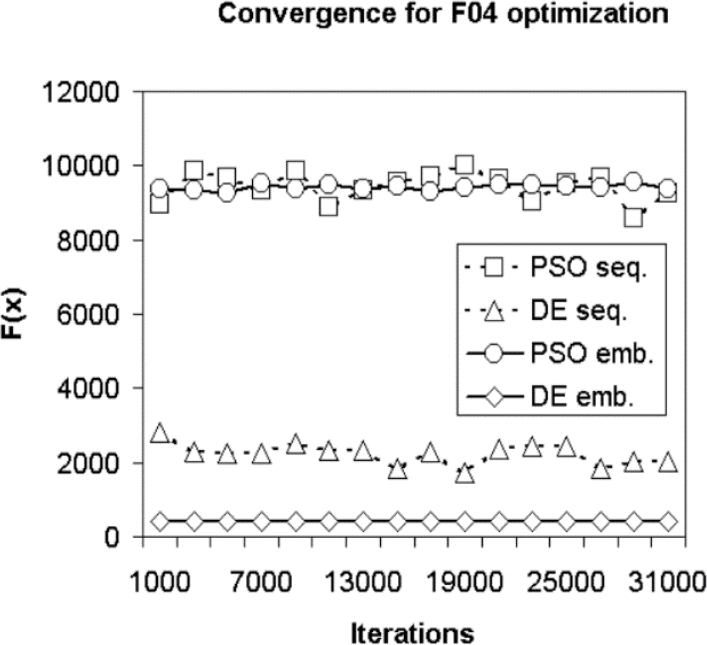
Fig. 6 For the function F04 with a variable number of iterations and with a number of 128 individuals
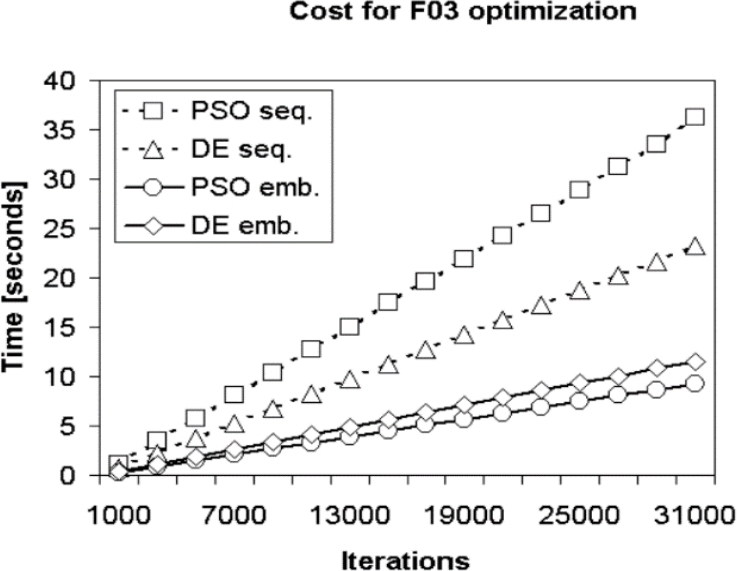
Fig. 7 The Cost metric for function F03 optimization with the number of individuals fixed to 128 and varying iterations
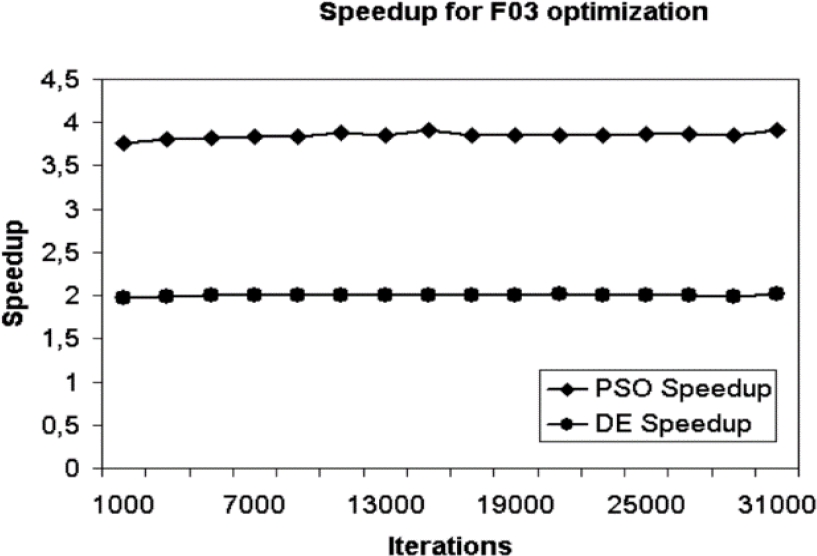
Fig. 8 Speedup metric for function F03 optimization with the number of individuals set to 128 and varying iterations
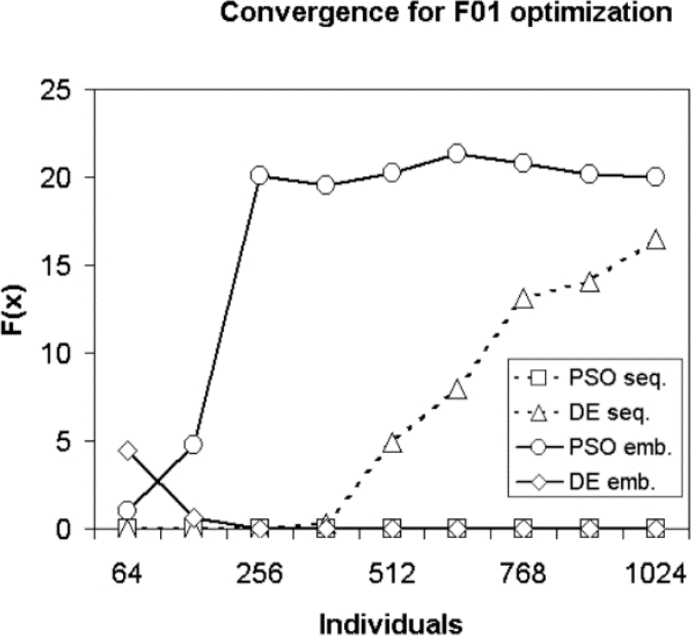
Fig. 9 Convergence for F01 optimization with iterations fixed to 15000 and varying the number of individuals
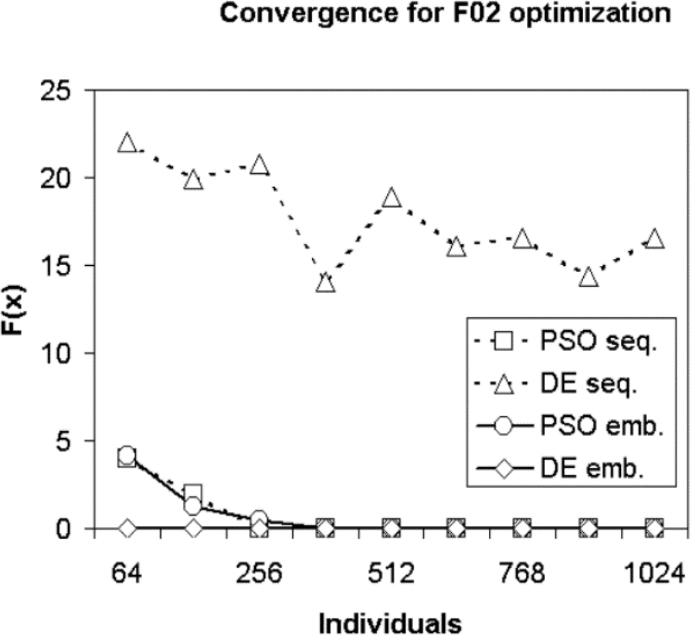
Fig. 10 Convergence for F02 optimization with iterations fixed to 15000 and varying the number of individuals
As mentioned above, the selected objective functions are multimodal, on the one hand functions F01 and F03 are separable functions, but on the other hand functions F02 and F04 are not separable. It should be remembered that functions with individual variables arranged in a linear combination are called separable functions.
A set of experiments was defined to be able to obtain the performance of the parallel implementations, a set of two experiments was carried out:
— Experiment 1. In this experiment the number of iterations will be changed and the performance measures for the parallel implementations of DE and PSO will be obtained. It starts with a number of iterations of 1000 and the number of iterations will be increased, in step of 2000, to 31,000; The number of individuals will be kept fixed at 128. The purpose of this first group of experiments is to obtain the time consumed, and from the data, it can be seen that in the optimization of Function F01 PSO in its sequential form it has a better convergence than the rest of the algorithms, followed by parallel DE, while sequential DE and parallel PSO algorithms they present an impoverishment in the results as the number of individuals increases. It is important to highlight the very different behavior of the parallel DE and PSO algorithms. In figure 10, it can be seen that during the optimization process of the F02 function, that the algorithm with the best convergence is the parallel DE algorithm, followed by the parallel PSO. a obtained, to generate the convergence curve of the parallel algorithms and compare the performance between the parallel algorithms and also between them and the sequential implementation in terms of the number of iterations.
— Experiment 2. For this set of tests the number of iterations was set at 15000 and there is a variable number of individuals. The number of individuals will vary starting from 64, 128, until 2014, with increments of 64. Tests are performed for parallel and sequential implementations of DE and PSO algorithms.
The objective of this experiment is to compare the consumed time and the convergence curve of the parallel algorithms with respect to sequential version in terms of the number of individuals. It should be remembered that for this experiment, the number of individuals increasing, for each experiment, in multiples of 64 individuals, this has the consequence that each individual generates parallel implementations of a thread and this is convenient since for this GPU architecture, NVIDIA recommends building blocks of thread with a size that is a 64 multiple, in order to obtain the best of the GPU resources [5].
Specifically, concerning Algorithm 1, PSO was implemented in the local version (i.e. each particle has a local neighborhood and knows which particle is global best and which is local best) the following parameters values were fixed for the tested functions:
(1) Population initialization. Setting up each particle of the initial population, by calculating an initial random number, calculating the values for the n-dimensional vectors corresponding to each xy position as well as v velocity.
(2) Fitness assessment. The fitness obtained from the xy position must be computed for each particle. If the fitness obtained by the current particle position has better value than pbx, then pbx should take the calculated fitness and update.
(3) Comparison. Calculate the position of the particle having the best fitness and compare with the best overall fitness gbx.
(4) Update. For every element of the vector x, of each particle, the velocity must be calculated and actualized according to the next mathematical statement:
where c1 and c2 are constants that weigh the social influence and individual learning; r1 and r2 are random variables, with values from 0 to 1, which represent the non-restricted movement for each particle, and the system inertia (w) is calculated as:
where itermax, iter, wmax, and wmin are the maximum inertia value, minimum inertia value, maximum iterations, and current iteration, respectively.
(5) Update. For each particle, the x value using the following equation:
(6) Loop. The repetition of steps 2 to 5 until reach the ending condition.
And neighborhood with size of 20 was defined for each particle in a random way. Concerning Algorithm 2, For the structure of the DE algorithm, the variant DE / rand / 1 / bin was chosen. The configuration of the algorithm parameters was as follows: the F parameter was configured with 0.6 for all the functions to be tested, on the other hand the CR parameter was configured according to the characteristics of each function, as recommended in [30]: For non-separable functions CR = 0.9 (F01 and F03) for separable functions CR = 0.0 (F02 and F04).
(1) Population initialization. Define initial population with N random individuals Xi,G for first generation G = 1.
(2) Evolution and fitness evaluation (Mutation step). For current generation G, and for each Xi,G vector, where i = 1, · · · , N , a test vector V is generated according with:
where r1, r2, r3∈ [1, N ] are assorted integers, and F must be grater than zero. F is a real constant factor which controls the difference variation. Integers values for r1, r2, and r3 must be randomly selected with an interval [1, N ] and must be different of current index i. So that N >= 4 individuals.
(3) Crossover step. In order to increase vector diversity, a trial vector U is defined, element by element as:
where j is the element index, randj is a uniform stochastic number between 0 and 1, and jrand is a randomly selected index from 1 to D, with D the dimensionality of the problem, which ensures that Ui,G+1 has one parameter, at least, from Vi,G+1. CR ∈ [0, 1] is the crossover probability and constitutes one control variable, which has shown to be determinant to find optimal values in functions with separable variables when CR is small.
(4) Comparison and updating (Selection step). To select the vector U that must turn a part of G + 1 generation, Ui,G+1 (trial vector) is compared to the target vector Xi,G. If U vector has a better fitness value than Xi,G then Xi,G+1 is set to U, otherwise previous Xi,G is retained.
(5) Repeat steps 2 to 4 until reach the termination condition (i.e. iterations).
The set of functions that were tested included functions with a constant number of individuals and a variable number of iterations for each function (F01, F02, F03 and F04), and the variants with constant iterations and a variable number of individuals (F01, F02, F03 and F04). For each reference function, each experiment was executed 30 times in each variant (Sequential, parallel, varying iterations and varying number of individuals). Thus, the fitness value (the average solution), the average time consumed and its standard deviation were recorded for all of the test functions.
5.1 Performance Metrics
To evaluate the performance of parallel implementations, traditionally a set of metrics is defined such as:
Computational cost is the processing time in seconds that a given algorithm consumes and is denoted by C. The inverse of computational cost is called computational performance T, so that:
The execution time improvement achieved is measured by Speedup S and expresses the number of times faster that the parallel implementation is, compared to the reference implementation:
where Tref is the performance of the sequential implementation and is our reference, Ttarg the level of compliance that presented the parallel version of the algorithm, after all it is the performance of the algorithm for a particular problem or function.
5.2 Experimental Results
This section reviews the behavior observed for both DE and PSO implementations, after testing variants with different iterations and with increasing numbers of individuals. The experimental results were recorded or each tested function for both kind of algorithms (parallel and sequential). After all our objective is to make a comparison between the parallel versions of DE and PSO, and show a comparison of their performance executing on Graphic Processing Unit card.
Because the quality of convergence, in most cases, population-based algorithms are very sensitive to their specific working parameters, particularly in an optimization process. (for example vmin, vmax, wmin, wmax, c1, c2 and neighborhood size for PSO, or they can be CR and F for DE) and with respect to the nature and class of the itself (that is, the objective function). Regardless of which algorithm has the best convergence, it is important to determine the effect of the parallelization of the code, as well as the effect of the variation of the number of iterations and number of individuals, both in the time consumed (computational cost) and in the general form of the convergence curve.
With the exception of function F04, the tested functions have an optimal value of zero. Due to the above, the process to obtain comparable graphs, the F04 graph was modified by adding the optimal value (12569.4866 for a dimension of 30) to display a convergence curve referred to zero and that all graphs are comparable to each other.
5.3.1. Results of the First Experiment
The experimental results obtained when the number of iterations is varied, and the number of individuals is fixed to 128, are graphed in Figures 3 to 8. Figure 3 shows the sequential implementation (abbreviated as PSOseq.), during F01 optimization, for the PSO algorithm that has the best convergence compared to the other sequential and parallel (emb. as short for embedded).
The sequential PSO algorithm has the best performance converging first to the global optimum at a value of approximately 3000 iterations, secondly the parallel DE, sequential DE, and parallel PSO algorithms. It is important to highlight the poor performance of the relative parallel PSO algorithm, see Fig. 3.
In Fig. 4, it can be noted that the best convergence, in the optimization of F02, is presented by the parallel implementation of the DE algorithm followed by parallel PSO. From the above, it can be noted that both parallel implementations have a better convergence with respect to the sequential ones.
During the F03 optimization process, see fig. 5, the parallel implementations of the DE and PSO algorithms get stuck in the local optimum closer to the global better than sequential versions, which get stuck in a local optimum further, from the best value (the global optimum), than the parallel implementations.
In the case of F04 optimization, see fig. 6, when comparing the best values obtained by the sequential and parallel algorithms, it was found that the best values were obtained by the parallel version DE algorithm, which stuck in a local optimum closer to the global optimum than the other algorithms, which are trapped in optimal locations further from the global optimum. It should be noted that in particular the F04 function turned out to be a difficult function to optimize for all the implemented algorithms.
On the one hand, the acceleration achieved by varying the number of iterations and the time consumed, its behavior can be seen in Fig. 5. On the other hand, the function F03 can be seen in the convergence process when optimizing with varying the number of iterations and in 128 the number of individuals, see Fig. 6.
Additionally, when the number of individuals is set to 128, it can see the convergence for the optimization of the function F04 and the iterations are varied, the experimental results have very similar behaviors and results in all the tested functions. For example, as can be seen in Fig. 7 and Fig. 8, the time consumed and the acceleration for the F03 optimization.
On the one hand, the acceleration achieved by varying the number of iterations and the time consumed, its behavior can be seen in Fig. 5. On the other hand, the function F03 can be seen in the convergence process when optimizing with varying the number of iterations and in 128 the number of individuals, see Fig. 6.
Additionally, when the number of individuals is set to 128, it can see the convergence for the optimization of the function F04 and the iterations are varied, the experimental results have very similar behavior and results in all the tested functions.
For example, as it can be seen in Fig. 7 and Fig. 8, the time consumed and the acceleration for the F03 optimization.
In the experiments, an acceleration produced by the GPU is appreciated that is practically invariable to changes when the number of iterations varies.
The acceleration achieved when a fixed number of individuals (128) is very small (2 for DE and 3.75 for PSO), primarily because the value of the population was set at 128 and it could be seen that, in the parallel implementations implemented, the GPU has an increase in the acceleration as the individuals are increased than when the iterations are increased [3] and, secondly, it is known that in the proposed implementations the arithmetic operations are not exploited in parallel, nor the unified memory instructions or shared memory.
5.3.2 Results of the Second Experiment
The experimental results correspond to the following parameters: variable number of individuals starting from 64 individuals and the number of iterations at a fixed value of 15000, after comparing the convergence curves of the first experiment and highlighting that 15000 iterations are capable of reaching a stable solution in the form of a local or global option, this can be seen in figures 9 to 14.
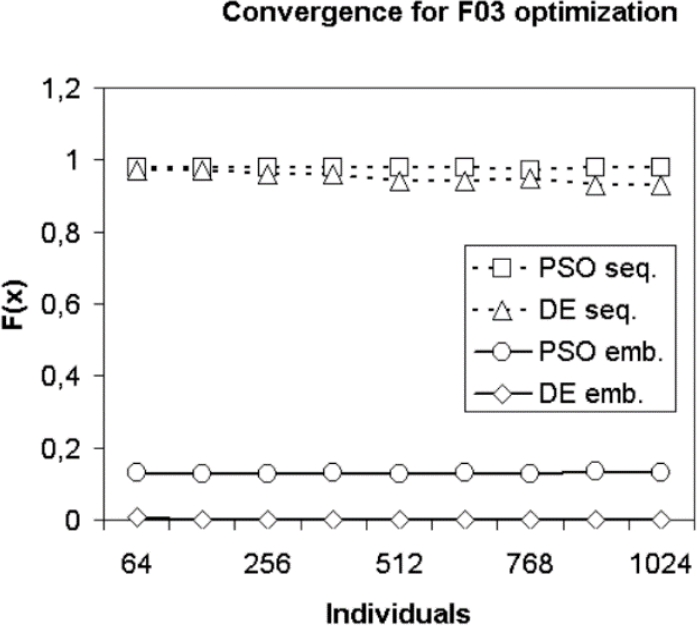
Fig. 11 Convergence for F03 optimization with iterations fixed to 15000 and varying the number of individuals
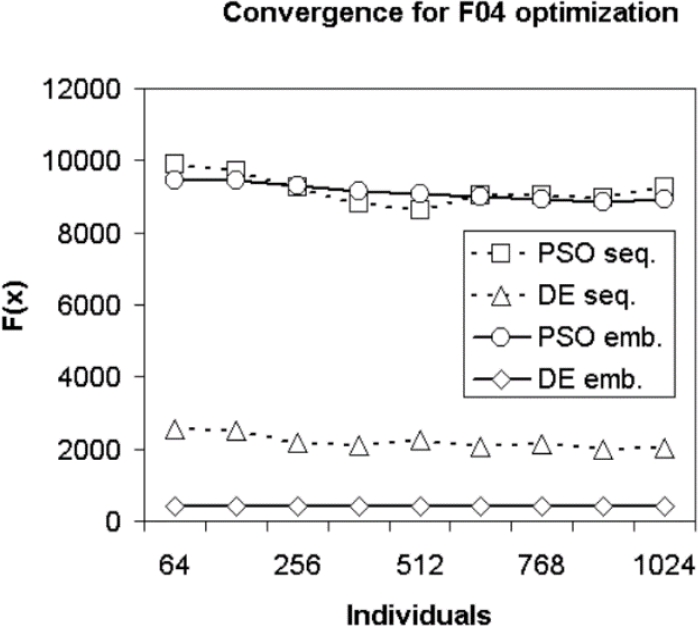
Fig. 12 Convergence for F04 optimization with iterations fixed to 15000 and varying the number of individuals
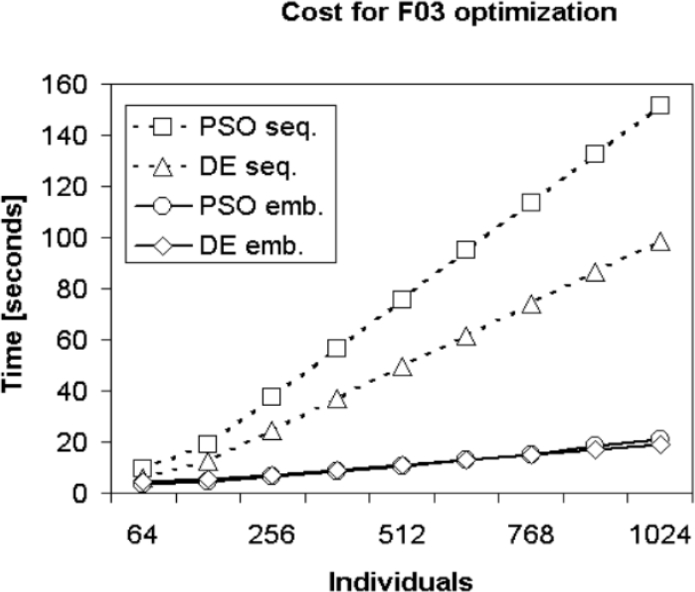
Fig. 13 Cost for F03 optimization with iterations fixed at 15000 and a varying number of individuals
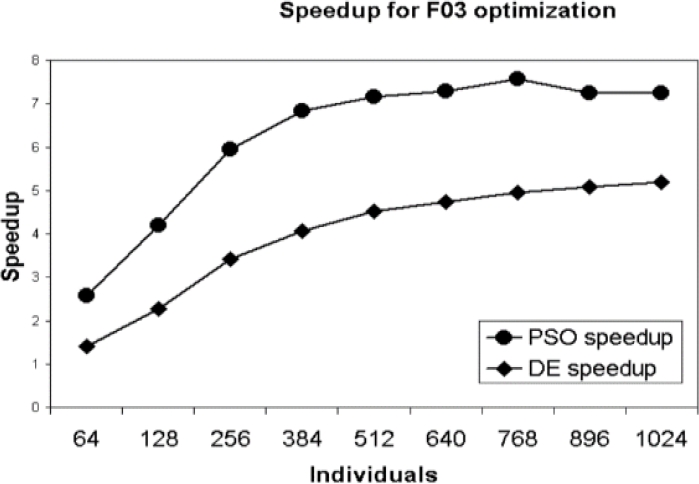
Fig. 14 Speedup for F03 optimization with iterations fixed at 15000 and a varying number of individuals
It can be seen that in the optimization of Function F01 PSO in its sequential form it has a better convergence than the rest of the algorithms, followed by parallel DE, while sequential DE and parallel PSO algorithms they present an impoverishment in the results as the number of individuals increases. It is important to highlight the very different behavior of the parallel DE and PSO algorithms. In figure 10, it can be seen that during the optimization process of the F02 function, that the algorithm with the best convergence is the parallel DE algorithm, followed by the parallel PSO.
Another result to highlight in this set of experiments is that both sequential implementations present a lower quality convergence with respect to the parallel implementations, however the DE presents a slower convergence. It can be seen that during the optimization of the F03 function, see fig. 11, the DE and PSO algorithms in their parallel implementation end up trapped in a local optimum of better quality (that is, closer to the global optimum) with respect to sequential implementations, which are stunted in local optimal far from global optimal.
During the optimization of the F04 function, presented in Fig. 12, it can be seen that the DE algorithm in its parallel implementation is stuck in a local optimum closer to the global optimum with respect to the rest of parallel and sequential implementations, which end up stuck in optimum local far from the global optimum.
Regarding the acceleration achieved and the time consumed when the number of individuals varies, in general, although the tested functions present different types of problems and are on the one hand non-separable functions and on the other hand separable functions, the experimental results are similar as well as their variants (in individuals and in iterations).
It can be seen, in Fig. 13 and Fig. 14, that the time consumed and the acceleration for the F03 optimization. It has been observed that the GPU improves the performance, when the individuals are increased, as well as the acceleration in the case of the proposed parallel implementations. It should be noted that the observed acceleration increased as the number of individuals in the populations increased. When the function F03 is graphed, with a variable number of individuals and with a fixed number of iterations at 15000, the convergence for optimization can be seen, see Fig. 11.
For the F04 functions case, with a variable value of individuals and with a number of iterations fixed at 1500, the Convergence for optimization F04 is shown.
6 Discussion
After having carried out the experiments and compiled the resulting data, it could be observed that in the parallel implementations, the acceleration achieved increases especially when the number of individuals increases more than when the iterations increase and the number of individuals remains fixed.
The behavior observed in the convergence curves can be explained by the fact that by increasing the number of individuals (DE) or particles (PSO), the threads executed are increased, and this allows the GPU to do a better management of the resources [5]. In the case of the other experiment, by coding parallel algorithms where only the iterations are increased, the GPU only repeats practically identical processes.
Therefore, it is more convenient to analyze the time consumed and the convergence curve of parallel implementation. In the case of the other experiment, by coding parallel algorithms where only the iterations are increased, the GPU only repeats practically identical processes. Therefore, it is more convenient to analyze the time consumed and the convergence curve of parallel implementations in algorithms where the number of individuals is changed, than when the number of iterations is varied. Regarding acceleration, it should be noted that the modest values reported here are susceptible to being improved using more efficient programming. It should be remembered that the algorithms used are originally sequential algorithms and that to be executed on the GPU they were migrated to parallel programming, it can be said that the sequential algorithms and parallel algorithms are identical in most of their modules, probably with the sole exception of the random number generation module. It should be noted that when sequential heuristics were passed to parallel programming for a GPU, it was observed that, in addition to the expected acceleration, a different behavior was also observed in convergence. In the case of our development, this change is due, in the first instance, to the way that the random numbers are calculated for sequential implementations with respect to the parallel ones.
Due to the nature of the parallelization process of the DE and PSO algorithms, random numbers must be generated differently from how they are generated in sequential programming.
Inside the GPU, the random number generation process is carried out starting with the generation of different seeds in an offline way (outside the GPU) and these seeds are passed to the graphics card, from this the GPU is able to generate its numbers from individual to individual, therefore the behavior of parallel and sequential implementation is different between each other.
In most experiments, parallel DE algorithm obtained the best performance during optimization of all tested functions except for F01, where the sequential PSO has a clear advantage over the other algorithms. It is important to highlight the change in convergence behavior between parallel and sequential implementation of the same heuristic (that is, PSO or DE).
The reduction of the execution time of a parallel code executed in a GPU is demonstrated by the experimental results, in addition the convergence to the global optimum has a significantly behavior changes with respect to the original sequential code.
On the one hand, this allows us to highlight that if a sequential algorithm performs good for a certain function, this does not imply that this algorithm, when implemented and coded for a parallel variant, will behave the same for the same problem, since it may perform poorly, regular or good (as it is clear from Fig. 9 for PSO when optimizing F01).
On the other hand, it implies that having a sequential algorithm that does not perform well in a particular function, it does not imply that this algorithm in an encoding of a parallel variant also behaves badly for the same function (as can be seen in Fig. 10 and Fig. 11 for DE when optimizing F02 and F03).
7 Conclusions
Sequential and parallel versions of the DE and PSO algorithms were presented, using CUDA as a parallel programming model in a multi-threaded GPU using. As a parallel programming methodology, a so-called integrated approach was used, where one thread per individual or particle was assigned. In addition to the self-acceleration introduced by the GPU parallel architecture, parallel deployments exhibited a different behavior with respect to sequential implementations, the above is a direct consequence of the strategies that were used for the generation of random numbers and how they should be generated in the GPU.
As results of the experiments for this comparative study, it was observed that the parallel DE algorithm had the best performance in the whole set of the tested functions, with the specified parameters of the algorithm and a significant dimensionality of 30. It should be noted that DE, adjusted by its parameters F and CR in an adequate and correct way that are dependent on the problem to be solved, can converge to the global optimum using as few individuals as 64 and in a small number of iterations as 3000.
Future research can focus on 5 possible avenues of work:
Carry out a set of experiments with a test bed with a greater number of functions and test parallel implementations in real-world problems and observe their performance in optimizing those problems.
Use heterogeneous architectures with GPUs, such as Beowulf cluster, where the calculation jobs are distributed by host and by thread.
Apply all the GPU programming strategies such as the intensive use of shared memory, the exploitation of the attached memory instructions and the parallelization of arithmetic operations, and the use of multiple threads to obtain a high algorithm parallelism of PSO or DE.
Test the behavior of other population heuristics such as: Genetic Programming, Genetic Algorithm, Evolutionary Strategies, and Ant Colony Optimization.
Test more fitness functions with higher dimensionality.











 nueva página del texto (beta)
nueva página del texto (beta)




