1. Introducción
En Colombia, específicamente en la Cordillera Oriental del sistema norandino, convergen importantes sistemas de fallas activas, entre los cuales se destacan el sistema rumbo-deslizante sinestral (Santa Marta-Bucaramanga), y las fallas inversas (Boyacá, y Soapaga); éstas dos últimas forman parte de la terminación sur del sistema de fallas de Santa Marta-Bucaramanga y definen el llamado Bloque Soapaga (ANH, 2008). El Bloque Soapaga con un área de aproximadamente 2272.3 km2 se localiza la Cordillera Oriental, en inmediaciones del departamento de Boyacá, Colombia. En este sector, se encuentra una importante sucesión Cretácica, la cual ha sido afectada por las fallas antes mencionadas. Estas fallas (Boyacá y Soapaga) separan sectores con distintos espesores de sedimentos Cretácicos. Los de menor espesor se encuentran en el bloque yacente de la Falla de Soapaga, en donde el espesor de los estratos del Valanginiano Superior al Maastrichtiano sólo alcanza 1500 m. Todo el bloque de Soapaga y sus alrededores constituye un área clave para la exploración de hidrocarburos en rocas del Cretácico, debido a que la materia orgánica no se ha sobremadurado como en otros sectores de la Cordillera Oriental (ANH, 2008).
Esto último ha motivado que durante los últimos años, se haya generado una gran cantidad de edades termocronológicas (Parra et al., 2009b; Mora et al., 2010; Ramírez-Arias et al., 2012; Saylor et al., 2012a, b; Silva et al., 2013) en una región de relativa complejidad debido a la convergencia de diversos sistemas de fallas (Falla de Bucaramanga, Falla de Soapaga y Falla de Boyacá) cuya interacción a lo largo del tiempo geológico es desconocida. La actividad de tales fallas y el efecto climático podría acelerar los procesos de advección de isotermas, lo cual se reflejaría en un incremento diferencial en las tasas de exhumación de bloques tectónicos delimitadas por fallas. La cuantificación de las tasas de erosión en estos bloques sólo es posible a través de modelado numérico termocinemático 3D inverso (Braun et al., 2006, 2012) en el cual se incorporan parámetros termales y flexurales locales. Esto es realmente novedoso como aplicación a lo largo de los Andes del Norte y permitiría el conocimiento detallado de la estructura termal de cualquier sector dentro de los Andes del Norte y cuencas sedimentarias adyacentes a la Cordillera Oriental de Colombia. El modelo inverso termocinemático existente más cercano (Andes de Mérida) fue presentado por Bermúdez et al., (2011). Con base en los datos de termocronología existentes, principalmente trazas de fisión en apatitos (o AFT por sus siglas en inglés) y (U-Th)/He en circón (Parra et al., 2009b; Mora et al., 2010; Saylor et al., 2012a, 2012b) se pretendió realizar la reconstrucción de la historia de exhumación del sector de la Cordillera Oriental donde confluyen las fallas de Boyacá y Soapaga, además de otros sistemas de fallas menores.
La Cordillera Oriental, es junto con los Andes de Mérida, las porciones más septentrionales de Los Andes del Norte de Suramérica. La cadena norandina ha sufrido dos procesos de deformación importantes que posiblemente ocasionaron los primeros pulsos de exhumación y posterior levantamiento de la Cordillera Oriental: 1) la acreción de material oceánico ocurrido desde el Mesozoico tardío al Cenozoico (Cediel et al., 2003) y 2) la intensa actividad tectónica que ha sufrido el área debido a la interacción de las placas Nazca, Caribe y Suramérica (e.g., Toro, 1990; Parra et al., 2009b; Mora et al., 2010). La Cordillera Oriental ha sido sobrecorrida h acia el este sobre el Escudo de Guayana, desarrollando una importante cuenca de antepaís hacia el este, conocida como la Cuenca Llanos (Toro, 1990, Bayona et al., 2013).
La geología expuesta de la Cordillera Oriental está dominada por rocas sedimentarias plegadas de edad mesozoica. A lo largo de la Cordillera Oriental, existen tres áreas donde el conjunto de rocas sedimentarias y metamórficas del Paleozoico son llamadas "macizos": 1) El Macizo de Quetame situado al este de Bogotá. 2) El Macizo de Santander, el cual representa la terminación norte de la Cordillera Oriental; la exhumación de este último guarda una estrecha relación con la Falla de Bucaramanga (van der Lelij et al., 2016; Amaya-Ferreira et al., 2017, 2020; Siravo et al., 2020), y finalmente, 3) el Macizo de Floresta, ubicado en la terminación sur de la falla antes mencionada. Conformado por rocas sedimentarias devónicas, y un plutón granítico paleozoico, el cual ha sido expuesto por las fallas de Soapaga y Boyacá (Tesón et al., 2013; Velandia et al., 2020).
Estas últimas se consideran como fallas de cabalgamiento relacionadas con la terminación sur de la falla rumbo-lateral sinestral de Bucaramanga (Boinet et al., 1989; Velandia y Bermúdez, 2018). Sin embargo, el carácter tectónico y la continuación de las fallas de Soapaga y Boyacá hacia el sur (Figura 1) no han sido todavía dilucidados (Velandia, 2005); además se desconoce el posible rol que podrían tener ambas fallas y otras menores presentes en la zona, sobre la exhumación de este sector de la Cordillera Oriental (Saylor et al., 2012a).
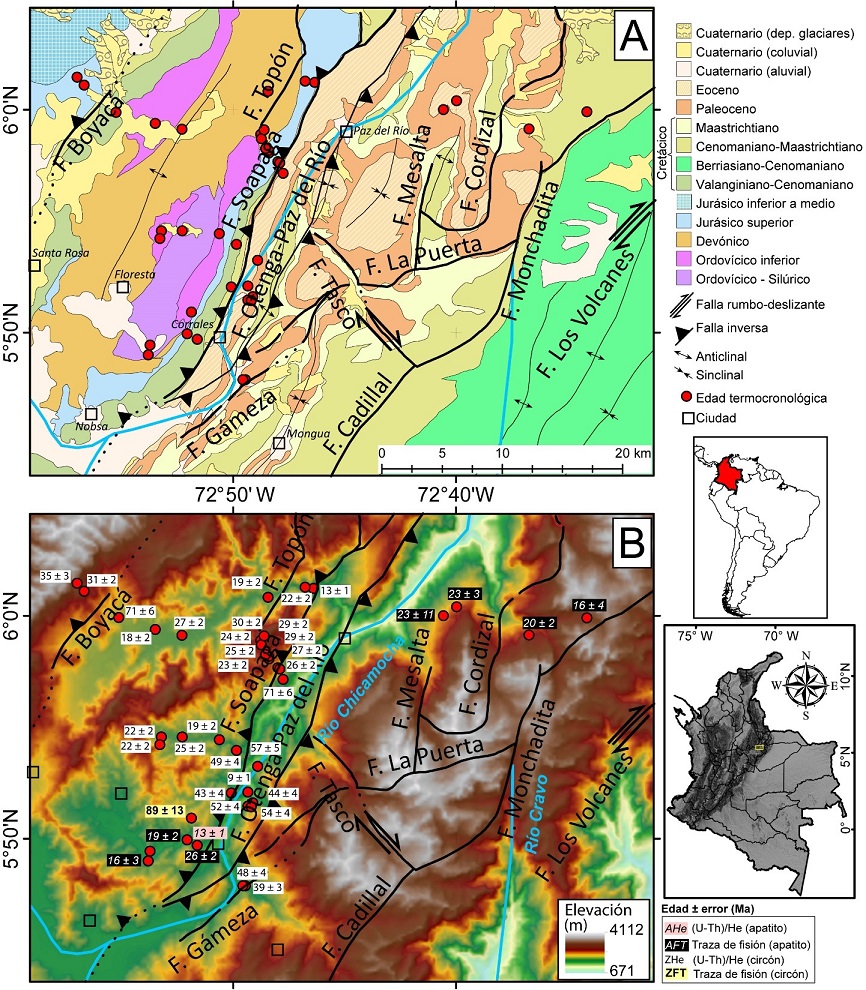
Figura 1 (A) Mapa geológico del área de estudio (Modificado de Gómez et al., 2015) y (B) Modelo de elevación digital ALOS a 30 m de resolución con fallas (Ulloa et al., 1998) y ubicación de las edades termocronológicas existentes (Parra et al. 2009b; Horton et al. 2010; Mora et al. 2010; Ramírez-Arias et al. 2012; Saylor et al. 2012b; Silva et al. 2013).
Adicionalmente, la cuantificación de la exhumación, y el aporte de la sismicidad al levantamiento superficial de este sector de la Cordillera Oriental no se conoce en detalle y mucho menos si las tasas de exhumación se han venido incrementado en el tiempo geológico motivado a un aumento significativo de las condiciones climáticas o tectónicas. Con la finalidad de establecer la influencia de las fallas presentes en la zona de estudio, discriminar los tiempos de exhumación, las velocidades de exhumación y la creación de relieve, se utilizó el modelado numérico termocinemático (PECUBE, Braun, 2003; Braun et al., 2012).
Las tasas de exhumación y los tiempos proporcionados por el modelo son comparados con tasas de levantamiento sísmico derivados de los datos de sismicidad actual con el propósito de discriminar si hoy en día el levantamiento superficial se ha venido incrementando o si por el contrario se ha reducido o permanece constante. En los alrededores del Bloque Soapaga existe un importante relieve, así para discriminar los efectos del clima y/o tectónica como posibles agentes controladores del relieve actual se incorporan mediciones geomorfométricas y se realiza un estudio detallado de los distintos parámetros obtenidos en el área de estudio.
2. Descripción de área de estudio
El área de estudio se encuentra localizada en el sector central de la Cordillera Oriental colombiana, departamentos de Boyacá y Santander, área de influencia de las fallas de Boyacá y Soapaga con un área total de 1686 km2 (Figura 1). A continuación, se presenta el contexto geológico-estructural del área de estudio.
2.1. CONTEXTO GEOLÓGICO
La Cordillera Oriental está limitada al oeste por la cuenca intermontana del Valle del Magdalena y al este por la cuenca antepaís de los Llanos, infrayacida por el Cratón Amazónico (e.g., Horton et al., 2010). En esta cordillera, vastas exposiciones de basamento metamórfico continental de bajo a alto grado se encuentran ubicados en la zona axial tomando el rumbo de la cordillera, como los macizos de Santander y Floresta (e.g., Ramírez-Arias et al., 2012; Tesón et al., 2013). La Cordillera Oriental está conformada por rocas sedimentarias de origen marino depositadas durante el desarrollo de grabénes triásico-jurásicos, así como rocas no marinas depositadas durante el desarrollo de una cuenca retroarco durante durante el Tithoniano-Necomiano hasta el Maastrichtiano (e.g., Sarmiento-Rojas et al., 2006; Kammer y Sánchez, 2006). El acortamiento Cenozoico producto de la convergencia oblicua de las placas Suramericana, Nazca y Caribe se evidencia en múltiples fases de deformación transpresional asociadas a tectónica de piel gruesa y delgada que inicia en el Cretácico tardío (e.g., Acosta et al., 2004; Saylor et al., 2012a; Bayona et al., 2013) y cuyo pico de mayor actividad se presenta durante el Plioceno-Pleistoceno (e.g., Saylor et al., 2012a).
Estructuras representativas en el área de estudio pueden ser observadas en la figura 1, en particular el Macizo de Floresta, el cual está delimitado longitudinalmente por la Falla de Boyacá al noroccidente y la Falla de Soapaga al suroriente, ambas con rumbo SO-NE, aflorando allí rocas con edades que oscilan entre el pre-Ordovícico y el Neógeno (Manosalva et al., 2017). En el área del Macizo de Floresta, datos termocronológicos y de proveniencia sustentan deformación Eocena asociada al movimiento inicial de la Falla de Soapaga (Parra et al., 2009a, 2009b, Saylor et al., 2012a), mientras que, en el flanco oriental de la cordillera, la exhumación asociada a la deformación contraccional inició por lo menos hace ~25 Ma (Parra et al., 2009a, Mora et al., 2010).
El dominio axial de la cordillera consiste en anticlinales apretados y sinclinales amplios relacionados a fallas de doble vergencia, asociadas a estructuras de despegue o pliegues de rompimiento "break-thrust folds" (Mora et al., 2010). Las fallas de Soapaga y Boyacá son fallas inversas que actúan como terminación en cola de caballo al sur de la Falla Bucaramanga (Toro, 1990; Dengo y Covey, 1993; Velandia, 2005; Kammer y Sánchez, 2006; Tesón et al., 2013). Sin embargo, trabajos recientes sugieren que ambas estructuras fueron capturadas, e incluso son ligeramente desplazadas por la Falla de Bucaramanga después de su reactivación durante la Orogenia Andina (Velandia y Bermúdez, 2018).
3. Materiales y métodos
Con el objeto de cuantificar la historia de exhumación del área de estudio, se realizó una compilación de datos termocronológicos existentes (Horton et al., 2010, Mora et al., 2010; Ramirez-Arias et al., 2012, Parra et al., 2009b, Saylor et al., 2012b), así como información de la Agencia Nacional de Hidrocarburos (ANH), Servicio Geológico Colombiano (SGC) y parámetros flexurales y termales obtenidos de Dengo y Covey (1993), Gómez et al. (2005), Braun y Robert (2005), Pérez-Gussinyé et al. (2008) y van der Lelij et al., (2016), relacionadas con la Cordillera Oriental colombiana (Figura 1; ver referencias en tabla 1). Se compilaron los datos de sismicidad del catalógo del Servicio Geológico Colombiano (http://bdrsnc.sgc.gov.co/paginas1/catalogo/index.php) para el período de tiempo comprendido entre 1993 y 2017, considerando únicamente los eventos cuya profundidad es menor a 15 km. Finalmente, se utilizaron los datos satelitales de precipitación promedio anual de la Tropical Rainfall Mission Measurement (TRMM) para el período comprendido entre 1998 y 2009 (Bookhagen y Strecker, 2008). Este último conjunto de datos tiene una resolución horizontal de 4 km y una resolución vertical de 250 m. Este material está disponible gratuitamente en http://www.geog.ucsb.edu/-bodo/TRMM/#tif.
Tabla 1 Parámetros termales y flexurales fijos utilizados para los modelos termocinéticos (PECUBE).
| Parámetro | Símbolo | Valor | Unidades |
|---|---|---|---|
| Espesor del modelo1 | zo | 40 | km |
| Densidad de la Corteza2 | ρc | 2700 | kg m-3 |
| Densidad del manto2 | ρm | 3200 | kg m-3 |
| Capacidad calorífica3 | C | 1000 | J kg-1K-1 |
| Conductividad termal3 | K | 25 | Wm-1K-1 |
| Temperatura superficial | T0 | 15 | ºC |
| Tasa de variación atmosférica | β | 6 | ºC km-1 |
| Difusividad termal3 | Κ | 25 | km2 Ma-1 |
| Comienzo de la exhumación5 | ts | 100 | Ma |
| Espesor elástico efectivo4 | Te | 30 | km |
| Módulo de Young2 | E | 70 | GPa |
| Coeficiente de Poisson2 | v | 0.25 | Adimensional |
| Factor de amplificación de la topografía | β | 1 | Adimensional |
Los superíndices indican referencias para algunos parámetros. 1: Dengo y Covey (1993). 2: Gómez et al. (2005). 3: Braun y Robert (2005). 4: Pérez-Gussinyé et al. (2008). 5: van der Lelij et al. (2016).
Los datos termocronológicos fueron utilizados con dos propósitos: i) controlar la convergencia de los modelos termocinemáticos tridimensionales (PECUBE; Braun, 2003; Braun et al., 2012) y ii) calcular las tasas de erosión asumiendo que la topografía está en equilibrio mediante el uso del código Age2Edot (Brandon et al., 1998; Ehlers, 2005; Schildgen et al., 2018). Mientras que los datos sísmicos se emplearon para calcular la energía sísmica liberada, la deformación sísmica y el levantamiento sísmico (o deformación sísmica vertical). Para obtener las variables topográficas y de la red de drenaje, se utilizó un modelo digital del terreno (MDE) de la misión ALOS, el cual consta con una resolución de ~ 30 m por pixel (https://www.eorc.jaxa.jp/ALOS/en/aw3d30/index.htm). A partir de este MDE, se extrajeron los índices de relieve local (R) y la Integral Hipsométrica (IH). En cuanto a los índices de la red de drenaje, se usó el MDE condicionado hidrológicamente para así reflejar de mejor manera la influencia de las lluvias en los procesos erosivos del paisaje. En las secciones subsiguientes se detallan de mejor manera estos procedimientos. Para cada sitio donde se dispone de una edad termocronológica, se construye una matriz con cada uno de los parámetros obtenidos y se discrimina los posibles controles tectónicos y/o climáticos sobre el relieve actual de la zona de estudio mediante un análisis de correlación de Pearson (Kendall y Stuart, 1973). A continuación se describen las bases de datos termocronológicas usadas, la base de datos de sismicidad compilada y cada uno de los métodos empleados en esta investigación.
3.1. DESCRIPCIÓN DE LA BASE DE DATOS TERMOCRONOLÓGICOS
En el presente trabajo se compilaron datos de distintos autores, los cuales son mostrados en la figura 1. En total, 75 edades reportadas en el área de estudio, y discriminadas de la siguiente forma: 15 edades obtenidas mediante el método de trazas de fisión en apatito (AFT), 13 edades de trazas de fisión en circón (ZFT), 1 edad (U-Th)/He en apatito (AHe), y 46 edades (U-Th)/He en circón (ZHe). Los datos fueron compilados a partir de los trabajos de Parra et al. (2009b), Horton et al. (2010), Mora et al. (2010), Ramírez-Arias et al. (2012), Saylor et al. (2012b), y Silva et al. (2013).
Los datos termocronológicos publicados fueron consolidados en una base de datos usando el Sistema de Información Geográfica ArcGIS versión 10.8, donde, adicionalmente, esta base de datos fue complementada con datos de flujo de calor (Pérez Gunsiyé et al., 2008), espesor elástico (modelo CRUST 1.0; Bassin et al., 2000; Laske et al., 2013), u otros datos geofísicos necesarios para realizar el modelado numérico.
La información se ordenó en formato (.shp) de ArcGIS, realizando mapas de distribuciones de edades y fallas sobre el mapa geológico-estructural (Figura 1), que permitieron observar densidad de datos y disposición de estructuras (fallas en superficie). Una vez seleccionadas las áreas de interés, se prepararon los archivos de entrada en formato de texto (.txt) en donde se establecen los parámetros de entrada para el código termocinemático, siendo estos parámetros: 1) edades de enfriamiento, 2) topografía, 3) parámetros de fallas, 4) parámetros topográficos, termales y flexurales.
Se compiló el código termocinemático 3D PECUBE usando GNU Fortran y lenguaje C. Para la visualización se utilizaron formatos VTK (Visualization Tool Kit) y los gráficos finales fueron generados con Paraview de Laboratorios SANDIA. Con el fin de conocer las configuraciones geométricas de fallas, el comportamiento de los datos, evaluar el número de fases de exhumación, cambios en la topografía y establecer estrategias para las inversiones, se realizaron los primeros modelos directos (forward modeling) utilizando los datos termocronológicos recopilados.
Para el modelado numérico termocinemático inverso PECUBE, se usó el cluster informático de alto rendimiento APOLO de la Universidad EAFIT (https://www.eafit.edu.co/apolo). El código PECUBE en su versión NA (Neighborhood Algorithm) se compiló usando las librerías de paralelización Intel® MPI (Multfabric Message-Passing library). Estando el código ya paralelizado, simplemente se compiló en el clúster con la finalidad de realizar las inversiones y variar el espacio de parámetros.
Para seleccionar la mejor familia de parámetros se usó el código NA-Bayes desarrollado por Sambridge (1999a, 1999b) y se consideró la familia de modelos con menor misfit y con significancia geológica.
3.2. TASA DE EROSIÓN A LARGO PLAZO
Las distribuciones de las edades termocronológicas correspondientes a AFT, ZHe, ZHe y AHe, pueden usarse para obtener predicciones de las posibles tasas de exhumación o de erosión a largo plazo, las cuales eventualmente se podrían comparar con el modelo de la intensidad de la erosión a corto plazo, así como con los posibles parámetros de control climático y tectónico. Se usó la rutina Age2Edot desarrollado por Brandon et al. (1998) y modificada esta última por Schildgen et al. (2018), que calcula tasa de erosión a largo plazo (km/Ma), basada en la edad del sistema (Ma), la profundidad de la temperatura de cierre (km), la temperatura de cierre (°C) y la tasa de enfriamiento (°C/Ma). Para llevar a cabo este procedimiento, se consideraron como parámetros para los cálculos cada uno de los cuatro sistemas termocronológicos, una difusividad térmica igual a 30 km2/Ma, el espesor cortical del modelo se asumió en 40 km, la temperatura en la base del modelo fue de 624.7 °C, siendo esta última obtenida de los modelos termocinemáticos inversos resultados de la presente investigación. Así, la figura 2 muestra, para el caso particular del método de trazas de fisión en apatito, la variación de las tasas de erosión con la edad. Una vez que se obtiene esta figura para cada uno de los métodos, el código arroja la tasa de erosión que le corresponde a cada edad.
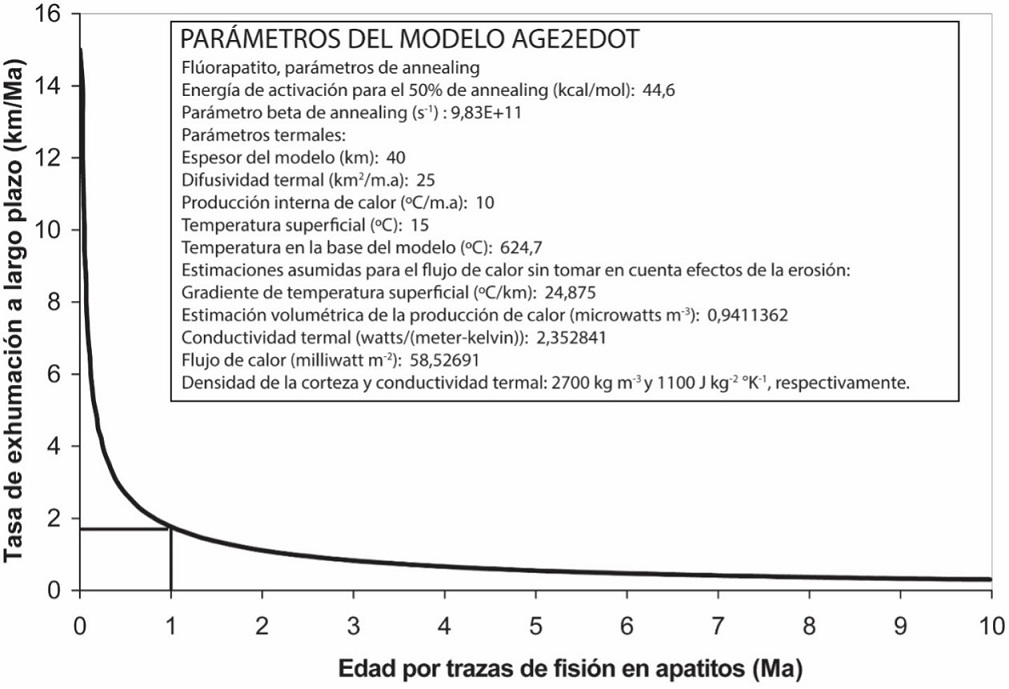
Figura 2 Relación entre tasa de erosión a largo plazo versus edades por trazas de fisión según el modelo unidimensional Age2edot (Brandon in Ehlers et al., 2005).
3.3. CÓDIGO TERMOCINEMÁTICO PECUBE
El código termocinemático 3D PECUBE, desarrollado por Braun (2003), constituye una parte fundamental de la termocronología cuantitativa (Braun y Robert, 2005; Braun et al., 2006; Braun et al., 2012).
Este código resuelve la ecuación del calor en tres dimensiones usando el método de elementos finitos el cual es una técnica numérica (Burden y Faires, 2002) que en el caso particular de PECUBE, permite resolver el siguiente problema de valor de frontera:
En donde: T(x,y,z,t) es la temperatura; ρ es la densidad de la corteza; c es la capacidad calórica; es la difusividad termal definida como el cociente entre la conductividad termal k y el producto de la densidad del manto y la capacidad calórica c.
Un valor típico de la difusividad termal es 25 km2 Ma-1 asumiendo k ≈ 2Wm-1K-1, ρ ≈ 3000 kg m-3 y c ≈ 1000WK-1 kg-1; H es la tasa de producción de calor; u,v,w son las velocidades de migración vertical de las rocas; T0 es la temperatura inicial; S(x,y,t) es la altitud en superficie considerando como base el nivel del mar; T1 es la temperatura en la base del modelo, asumiendo que está localizada a z = -L; TMSL temperatura al nivel del mar; β es la tasa de variación atmosférica.
En este modelo, en lugar de definir el flujo de calor es posible usar la temperatura basal, la cual simplifica los cálculos termales.
La ecuación 1 predice la edad en la cual pasa el termocronómetro (mineral de interés) a través de la temperatura de cierre, usando diferentes sistemas termocronológicos. En este caso, la ecuación del calor detecta si un bloque de la corteza está siendo afectado por procesos termo-tectónicos (movimiento vertical u horizontal o erosión). En los modelos que empleamos inicialmente, suponemos que no hay influencia del flujo de fluidos, y que la transferencia de calor por advección y conducción de rocas son los mecanismos dominantes de transferencia de calor. Este supuesto es importante porque permite contrastar zonas con alto flujo de calor observado. Es importante mencionar que se realizó más de un modelo directo donde se variaron distintos parámetros. A continuación se proporcionan más detalles del código PECUBE.
PECUBE emplea una mezcla de los métodos Lagrangiano y Euleriano para el campo de fluidos; ésta es una forma de mirar el movimiento del fluido, que se enfoca sobre ubicaciones específicas en el espacio a través del cual éste se distribuye (Braun, 2003). Estas especificaciones pueden ser aplicadas a cualquier marco de referencia del observador y en cualquier sistema de coordenadas empleado o usado dentro del marco de referencia escogido. Esto permite a PECUBE producir frecuentes re-interpolaciones del campo de temperatura en la dirección vertical. Así se calculan los caminos tiempo-Temperatura (t-T) obteniendo las edades termocronológicas para los minerales empleados.
3.3.1. SELECCIÓN DE LOS MEJORES MODELOS DIRECTOS
La selección de un buen modelo directo es basada en el cálculo del "misfit" (norma L2 o error cuadrático medio; Braun, 2003), el cual se estima mediante la siguiente expresión:
Donde n es el número de observaciones, tobs y tcal corresponde a las edades observadas y predichas por PECUBE para cada una de las muestras i.
3.3.2. ALGORITMO DE ENTORNO VECINO (NEIGHBORHOOD ALGORITHM; NA)
Una vez que se ejecuta el código termocinemático en su versión directa (forward), es necesario para entender cómo los diferentes mecanismos de exhumación y modelos termocinemáticos controlan la distribución de edades, realizar una exploración robusta del espacio de parámetros, lo cual sólo es posible a través de las inversiones en el cual PECUBE está acoplado con el algoritmo NA (Sambridge 1999a, 1999b; Herman et al., 2007; Campani et al., 2010; Robert et al., 2011; Braun et al., 2012).
El NA es un procedimiento numérico de dos etapas, el cual sirve para calcular los estimados Bayesianos de los parámetros de entradas para problemas inversos no lineales (Valla et al., 2010; Glotzbach et al., 2011). La primera etapa o fase de muestreo, es un método de búsqueda iterativa; el muestreo se concentra sobre regiones del espacio multidimensional de parámetros, en la cual la función misfit es optimizada numéricamente. El espacio de parámetros se divide en celdas de tipo Voronoi centradas sobre cada modelo muestreado, el cual representa el entorno cercano sobre cada punto. Una cierta cantidad de modelos directos con mejor ajuste (mayor al 50%) son usados para definir nuevas celdas Voronoi y así redefinir un nuevo espacio de parámetros. Este nuevo espacio de parámetros es muestreado durante la próxima iteración de forma aleatoria, eventualmente convergiendo hacia una de varias familias que minimiza la función misfit dada por la ecuación 2.
Posteriormente se usa el Criterio de Información Bayesiana (BIC por sus siglas en inglés; Schwarz, 1978) para la selección del modelo con diferente número de parámetros. Cuando se estiman parámetros de modelos usando estimación por máxima verosimilitud, es posible incrementar la verosimilitud añadiendo parámetros, lo cual puede resultar en un sobreajuste de los datos (Glotzbach et al., 2011). El BIC resuelve este problema introduciendo un término de corrección para el número de parámetros en el modelo. Así, el BIC vendría dado por la siguiente expresión:
Donde Lmax es la máxima verosimilitud obtenida para el modelo (L = e -misfit), k es el número de parámetros libres y n es el número de observaciones, respectivamente.
La resolución de los parámetros es asegurada mediante la función de densidad de probabilidad marginal asociada (PDF por sus siglas en inglés) obtenida mediante el remuestreo del conjunto de modelos y es controlada por la función de densidad de probabilidad posterior (PPD por sus siglas en inglés). Finalmente, la función log (PPD) es simplemente la función logarítmica de la verosimilitud L.
3.3.3. FILOSOFÍA DEL MODELO
El área de modelo corresponde a una región rectangular de 29.5 km x 57.16 km para un total de 1686.22 km2, dentro de la cual se consideró como estructura principal la Falla de Soapaga, situada en el centro del área de estudio, mientras que la Falla Boyacá se sitúa en el borde noroccidental del bloque tridimensional considerado. Se asumió en el modelo un ángulo de 30° de ambas fallas y una profundidad de 15 km (Toro, 1990). A cada lado de la Falla de Soapaga se asume que los bloques son independientes, proporcionando a cada sector una tasa de exhumación distinta. La temperatura en la base del modelo se consideró variable entre 300 a 900°C, la temperatura superficial de 15°C, la tasa de producción de calor (HP) se asume variable entre 0 a 8 μWm-3, el espesor del modelo se consideró fijó en 40 km. El tiempo de inicio de cada fase de exhumación se asume variable entre 0 a 100 Ma, y las velocidades de exhumación para cada pulso se consideró variable entre 0 a 2 km Ma-1. Los rangos escogidos son relativamente amplios lo cual permite una mejor búsqueda de los parámetros óptimos por parte del algoritmo del Entorno Vecino (Braun et al., 2012). En la figura 3 se puede apreciar la configuración inicial del modelo. En las tablas 1 y 2 se presentan los parámetros fijos y variables considerados en el modelado numérico.
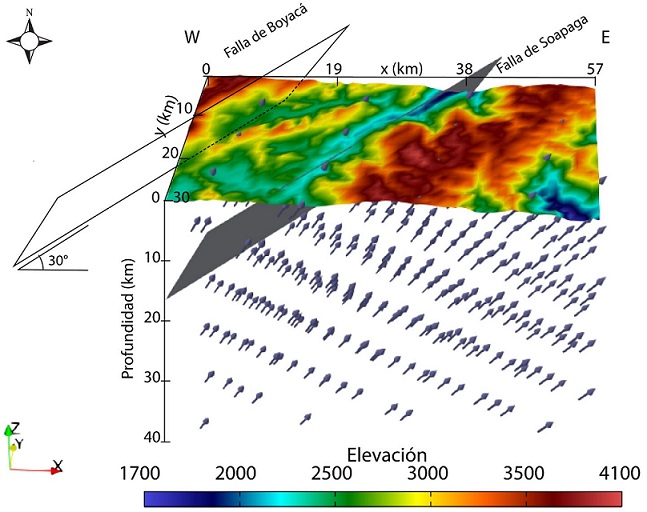
Figura 3 Configuración cinemática inicial del modelo PECUBE, las flechas azules indican los campos de velocidad de exhumación en cada uno de los bloques situados a ambos lados de la Falla de Soapaga.
Tabla 2 Parámetros considerados variables en el modelado inverso termocinemático.
| Parámetro | Símbolo | Rango de variación | Unidades |
|---|---|---|---|
| Producción de calor | A | 0-8 | μWm-3 |
| Temperatura en la base del modelo | Tz | 300-900 | ºC |
| Tiempo de inicio de la exhumación | tEi | 0-100 | Ma |
| Tasa de exhumación de cada fase i | Ei | 0-2 | km Ma-1 |
| Número de fases de exhumación | i | 1-3 |
Los tiempos de cada pulso de exhumación que el modelo termocinemático PECUBE predice pueden llegar en algunos casos hasta valores menores a 0.1 Ma. Sin embargo, esto último depende de la distribución de edades observadas en la zona de estudio. Así con la finalidad de comparar las tasas de exhumación (o levantamiento de la columna de rocas) a largo plazo con las que ocurren hoy en día (corto plazo), se estiman tasas de levantamiento a partir de la deformación sísmica. Al igual que Braun et al. (2009), si consideramos u el levantamiento sísmico, cómo el levantamiento vertical generado por la deformación sísmica, el cual corresponde a la cantidad de levantamiento de roca predicha a partir de la liberación de energía sísmica medida en los últimos 24 años (período de tiempo de la base de datos sísmica) y extrapolada en los últimos 5 Ma. Es posible comparar las tasas derivadas de la termocronología con las tasas de levantamiento derivado del patrón sísmico. Esta extrapolación puede realizarse sin problema alguno ya que el levantamiento u depende de los valores a y b de la relación de Gutenberg y Richter (1954), los cuales a su vez incluyen implícitamente los períodos de retornos de los sismos.
Sin embargo, es bien sabido que esta relación cambia a través de los años en una región, a lo largo del ciclo sísmico, y particularmente luego de la ocurrencia de un sismo mayor en el área. Por ende, esta comparación tiene que hacerse con cautela, y conociendo estas limitaciones. La relación antes mencionada es explicada a continuación en la siguiente sección.
3.4. DESCRIPCIÓN DE BASE DE DATOS SISMOLÓGICA
Se cuenta con 356 datos de sismicidad para 24 años, entre 1993 y 2017, donde no se tienen datos para el año 2000. Se registró el mayor número de eventos para los años: 2017 (30), 2016 (39), 2011 (36) y 2003 (27). Se identificaron dos zonas (Figura 4A) al este de la falla de Soapaga con 117 y 53 eventos, respectivamente. Un evento de magnitud 5,4 se registró en julio de 1999 (latitud 6.073° N, longitud -72.7270° W, profundidad de 2.9 km), seguido en orden de magnitud, se presentaron otros dos eventos: diciembre de 2001, magnitud de 4.4 (latitud 5.9430° N, longitud -72.5220° W, profundidad de 0.9 km) y en agosto de 2002, magnitud de 4.0 (latitud 5.9360° N, longitud -72.5580° W y a una profundidad superficial).
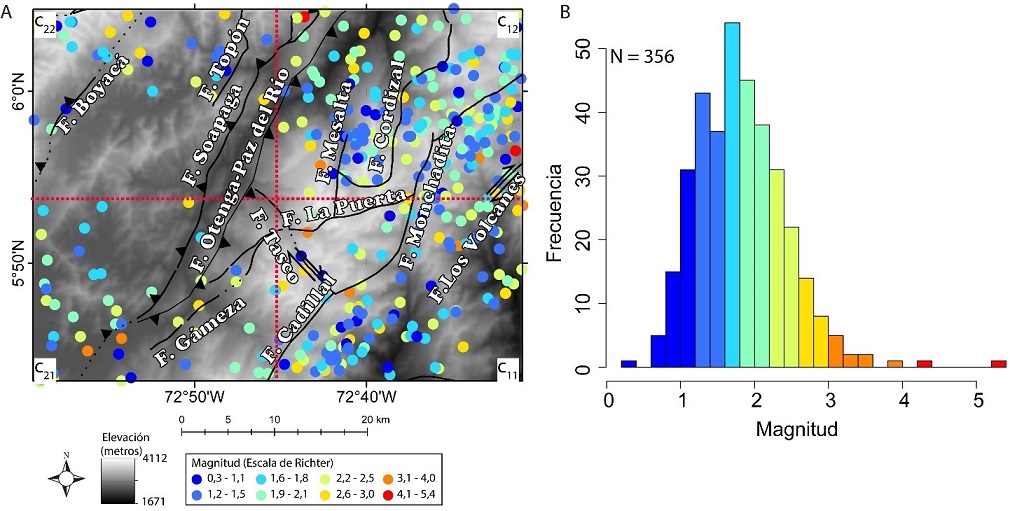
Figura 4 (A) Distribución de eventos sísmicos y localización de fallas activas (Ulloa et al., 1998). (B) Relación magnitud-frecuencia de la base de datos sismológica. c11, c12, c21, y c22 denotan los cuadrantes en los que fue dividida la zona para la comparación de los parámetros a y b de la relación Gutenberg y Richter (1954). N representa el número de sismos observados entre 1993 a 2017.
La figura 4A muestra la distribución de los eventos sísmicos, donde los símbolos varían de acuerdo con la magnitud de los eventos sobre un fondo de los principales sistemas de fallas activas. En la figura 4B, se muestra un histograma de los eventos analizados en este trabajo. La zona se caracteriza por presentar una mayor cantidad de eventos entre 1.0 a 2.8 de magnitud, y apenas un evento de magnitud 4 y otro de magnitud 5, respectivamente.
3.4.1. ENERGÍA SÍSMICA
Con la base de datos de sismicidad, calculamos la liberación de energía sísmica (Se), utilizando las magnitudes locales según la expresión de Gutenberg y Richter (1954):
Los valores de los parámetros a y b se estimaron mediante un ajuste al cuadrado mínimo de las relaciones magnitud-frecuencia acumuladas construidas a partir de todos los terremotos registrados en la región. Generalmente, el valor a está relacionado con la actividad sísmica y por lo tanto con el tiempo y el volumen de la ventana considerada. El valor b es uno de los parámetros estadísticos más importantes para describir las propiedades de escala de tamaño de la sismicidad; los valores b cambian aproximadamente en el rango de 0.3 a 2.0, dependiendo de las diferentes regiones. Sin embargo, las estimaciones medias a escala regional del valor b suelen ser iguales a 1 (Frohlich y Davis, 1993).
Muchos factores pueden causar una perturbación del valor promedio de b (b~1.0); las regiones que tienen valores b más bajos son probablemente regiones sometidas a un mayor esfuerzo de cizallamiento aplicado después de la perturbación principal, mientras que las regiones que tienen valores b más altos son zonas que han experimentado un deslizamiento. Regiones con valores b altos provienen de zonas que tienen una mayor complejidad geológica, lo que indica la importancia de las zonas de fracturas múltiples; un valor bajo de b puede ser relacionado con un bajo grado de heterogeneidad de las tensiones y deformaciones medias y grandes de las fracturas, la alta velocidad de deformación y la actividad de grandes fallas. Las anomalías de los valores b pueden deberse a anomalías en el gradiente térmico o la heterogeneidad de la corteza (Bayrak y Öztürk, 2004).
3.4.2. DEFORMACIÓN SÍSMICA
Los valores de liberación de energía sísmica se acumularon dentro de círculos con un radio de 1 km alrededor del epicentro de cada terremoto. Adicionalmente, utilizamos la base de datos sismológicos compilada para estimar la distribución actual de la tasa de deformación frágil, que puede extrapolarse a través del tiempo geológico utilizando la relación magnitud-frecuencia observada del terremoto (Gutenberg y Richter, 1954). Para calcular la tasa de deformación frágil, utilizamos la siguiente expresión (Braun et al., 2009):
En esta última expresión, a y b fueron definidas anteriormente; Mmax, es la magnitud máxima observada, aunque en este caso fue sustituida por la magnitud puntual porque no hay un cúmulo significativo de eventos sísmicos en las superficies de erosión; μ es el módulo de Young o el módulo de elasticidad longitudinal. En este trabajo, se utilizó un valor estándar de 1x1010 Pa para los primeros 15 km de la corteza (Turcotte y Schubert, 2002). ΔV representa el volumen de la corteza el cual es calculado para el área de estudio. Se calcula el área de la zona y se multiplica por 15 km que representa la profundidad de la zona de transición entre comportamiento frágil-dúctil. Finalmente, como se mencionó anteriormente los terremotos fueron observados en un período de tiempo Δt = 24 años.
3.4.3. DEFORMACIÓN VERTICAL O LEVANTAMIENTO SÍSMICO
Es posible describir la deformación actual de la zona de estudio por un acortamiento horizontal geográficamente variable pero verticalmente uniforme a un ritmo ἑ igual a la tasa de deformación sísmica frágil εH De acuerdo con el principio de conservación de masa a escala de la litósfera, esto implica que el acortamiento horizontal debe ser acompañado de un engrosamiento vertical a una tasa ἑV = -εH, suponiendo que la deformación horizontal en una dirección perpendicular a la dirección de máximo acortamiento es insignificante, y asumiendo además que el estado actual de compresión a lo largo de la Cordillera Oriental se ha incrementado desde los últimos 5 Ma al presente (Siravo et al., 2018, 2020), es posible estimar la cantidad total del engrosamiento experimentado en la zona integrando la tasa de deformación vertical calculada sobre los últimos 5 Ma como:
La deformación vertical calculada puede usarse para calcular el engrosamiento litosférico local y, asumiendo una condición de equilibrio isostático local, la cantidad de levantamiento u sobre los últimos 5 Ma está dada por:
Donde hc es el espesor cortical en cada píxel de la zona de estudio obtenido del modelo CRUST 1.0 (Bassin et al., 2000; Laske et al., 2013), ρc y ρm son las densidades estándares (promedio) de la corteza y el manto, respectivamente.
3.5. ESTIMACIÓN DE PARÁMETROS GEOMORFOLÓGICOS
Las variables geomorfológicas, tanto topográficas como de la red de drenaje, son fundamentales para entender la evolución del paisaje y entender cuáles mecanismos, ya sea tectónicos y/o climáticos, han influenciado en su formación. En este trabajo, se evaluaron dos índices a nivel topográfico (relieve local e integral hipsométrica) y uno al nivel de la red de drenaje (índice de empinamiento normalizado). Para el cálculo de estos parámetros se emplearon los modelos de elevación digital a 30 metros del sensor ALOS previamente mencionado.
3.5.1. RELIEVE LOCAL E INTEGRAL HIPSOMÉTRICA
Los índices del relieve local y de la integral hipsométrica (HI) tienen como finalidad revelar información sobre el estado evolutivo del paisaje en una escala de tiempo que puede ir hasta 106 años (Pike y Wilson, 1971). Estos índices fueron calculados y ploteados a través de la herramienta estadísticas focales del software ArcMap® versión 10.8 para cada píxel del modelo de elevación digital anteriormente mencionado. En este caso se consideró el área total y no las cuencas dentro de la zona de estudio. El relieve local se obtiene al sustraer la elevación mínima de la elevación máxima para una ventana de análisis circular, la cual se definió de cinco kilómetros de radio. Se usa este valor para extraer información del paisaje a nivel regional incluyendo los bloques de las fallas de estudio. La HI se puede calcular usando la siguiente ecuación:
Donde me es la elevación promedio, mne en la elevación mínima y mxe es la elevación máxima en una ventana de análisis, que, para este caso, se usa la misma del relieve local (5 km). Valores de HI mayores a 0.5 indican un paisaje juvenil que puede estar respondiendo a un rejuvenecimiento topográfico producto de un levantamiento de la superficie o cambios litológicos. Valores entre 0.3 y 0.5 hacen relación a paisajes en equilibrio, mientras que valores de HI<0.3 se asocian a paisajes seniles donde los procesos erosivos predominan (Bustos et al., 2013).
3.5.2. ÍNDICE DE EMPINAMIENTO (KSN)
Para el análisis de la red de drenaje, se evaluó el índice de empinamiento del canal normalizado (ksn por sus siglas en inglés). Este índice expresa la pendiente normalizada de una red fluvial en un espacio de coordenadas logarítmicas área-pendiente. Este índice es importante para la identificación de procesos tectónicos activos y se relaciona a la concavidad (θ) según la siguiente ecuación (Hack 1973; Flint 1974):
Donde S corresponde a la pendiente del canal, ksn es el índice de empinamiento normalizado del canal, A es el área de la cuenca de drenaje y θ es el índice de concavidad.
Kirby y Whipple (2001) proponen trabajar esta ecuación con un índice de concavidad de referencia (θref) a partir de la media regional de los valores de θ, en segmentos del canal sin anomalías topográficas, y sugieren que el θref calculado se debería situar en un intervalo de 0.4 ≤ θ ref ≤ 0.6. Para una red fluvial en condiciones topográficas normales, la curva log área vs log pendiente no presentará datos anómalos y se representará por una línea recta con pendiente negativa. Cuando se presentan knickpoints (de tipo: tectónicos, litológicos, climáticos o erosivos) a lo largo del drenaje, existirán variaciones significativas. Anomalías con quiebres verticales pequeños (vertical-step knickpoint) y discretos no tienen un significado tectónico directo (Kirby y Whipple, 2012), en contraste cuando se observan puntos de quiebre de pendiente significativos (slope-break knickpoint), éstos se generan como respuesta a cambios persistentes espaciales o temporales. Para evaluar actividad neotectónica, este índice se utiliza principalmente representado en una vista en planta sobre un mapa, facilitando la delimitación de zonas activas (e.g., Wobus et al., 2006; Dalman, 2015; Rizwan et al., 2016; Dey et al., 2019). En este trabajo, usamos un θref = 0,45 para el cálculo del índice ksn. Este último se determinó utilizando el código Topo-toolbox, herramienta ejecutable en Matlab® 2018 y desarrollada por Schwanghart y Kuhn (2010). Una vez determinados los valores del índice de empinamiento para cada una de las subcuencas, se realiza una interpolación geoestadística, para obtener en planta zonas de densidades, que representan áreas con los mayores valores de ksn.
4. Resultados
4.1. MODELAMIENTO INVERSO TERMOCINEMÁTICO
La mejor familia de modelos inversos es aquella en la cual se emplean dos fases de exhumación para la Falla de Boyacá y una sola fase para la Falla de Soapaga. Esta familia presentó el menor BIC (687) y está conformado por 10100 modelos directos. La figura 5 representa los resultados de nuestra familia preferida de modelos, donde cada punto de colores representa un modelo directo. El asterisco en color negro representa el modelo directo de menor misfit (0.77). Las curvas grises y negras representan las marginales 2D Bayesianas; la zona en gris delimita los modelos que poseen una confiabilidad de 95%, mientras la zona en negro representa los modelos con 99% de confiabilidad, respectivamente. Las curvas de densidades colocadas en la parte superior y a la derecha de cada figura representan las marginales en 1D y la mejor familia de modelos es aquella que presentó un menor valor de misfit. En este caso, la inversión de parámetros sugiere dos pulsos de exhumación para el sector entre la fallas de Boyacá y Soapaga, un primer pulso t1FB desde 69.09 hasta 15.73 Ma con un tasa de exhumación cercana a 0.9062 km/Ma y un segundo pulso de exhumación t2FB desde 15.73 al presente, con una tasa de exhumación de 0.1613 km/Ma. Esta tasa se obtiene sumando las dos tasas de exhumación obtenidas de la primera y segunda fase. Esta diferencia en tasas de exhumación se debe a que generalmente una vez que se produce un primer pulso de exhumación muy rápido es necesario que exista posterior a este evento un reajuste isostático lo cual ocasiona que disminuya la tasa de exhumación (Spotila, 2005). Así, se observa que ocurre un cambio de la geometría de la falla a 15.73 Ma. En contraste, la zona situada en el bloque yacente de la Falla de Soapaga, exhibe un pulso de exhumación continuo desde 22.65 Ma al presente con una tasa de exhumación de 0.4867 km/Ma.
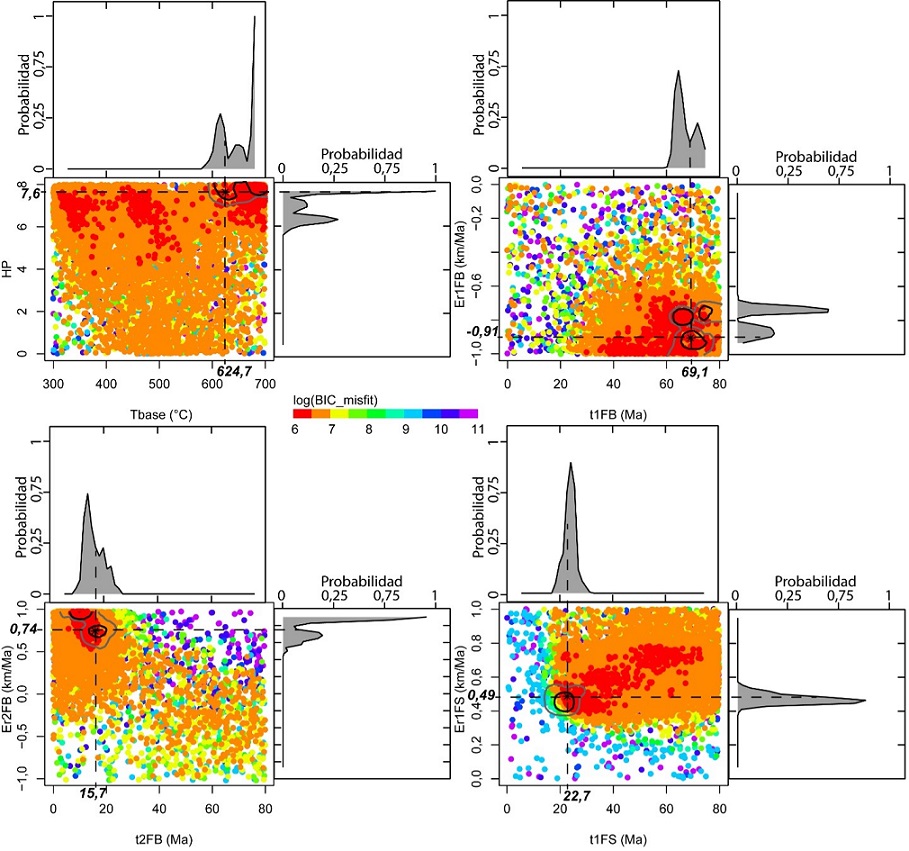
Figura 5 Resultados del modelado termocinemático inverso. Cada punto de color corresponde a un modelo forward, esta figura está constituida por 10100 modelos forwards. Se muestran las marginales Bayesianas en 1D y 2D. Las curvas gris y negra en las marginales 2D corresponden a los modelos con una confiabilidad de 95 y 99% respectivamente.
Los parámetros obtenidos para el modelo directo de menor misfit (0.77), el cual es denotado con asterisco en la figura 5, es utilizado para predecir edades en cada píxel del modelo de elevación digital, donde edades predichas son comparadas con las edades observadas, con la finalidad de que pueda analizarse la reproducibilidad del modelo. En la figura 6, se realiza una comparación entre edades observadas y predichas por el modelo de menor misfit. Considerando los errores sobre las edades, el modelo de menor misfit puede predecir con eficiencia las edades observadas para los sistemas AFT (Figura 6B) y ZHe (Figura 6C) que son las más abundantes. Sin embargo, para los sistemas AHe y ZFT (Figuras 6A y 6D, respectivamente) donde se disponen de pocas edades observadas para cada sistema, no se observa un buen ajuste. La razón de esto puede deberse a dos factores: i) generalmente las edades AHe y ZHe son obtenidas promediando edades individuales por cristales, pero los mismos pueden tener una alta dispersión producto de distintas fuentes de error entre las cuales se destacan: el tamaño del grano, el daño por radiación, la fragmentación del grano, la zonificación U y/o Th, las complejas relaciones intragranulares eU, la implantación del He, las incertidumbres en el cálculo del factor de eyección alfa, las inclusiones minerales, las inclusiones de fluidos ricos en He y la prolongada residencia en la zona de retención parcial del He (Wildman et al., 2016; Danisík et al., 2017; Hueck et al., 2018). Además, las imperfecciones en los cristales, como los daños en las vacantes y los microeventos cristalográficos también pueden afectar a la difusión de He (Gerin et al., 2017; Zeitler et al., 2017). A partir de todos estos factores, una variación significativa de las características composicionales y cristalográficas podría producir una dispersión intramuestra a edades de He superiores al 50% (por ejemplo, Wolfe y Stockli, 2010; Wildman et al., 2016).
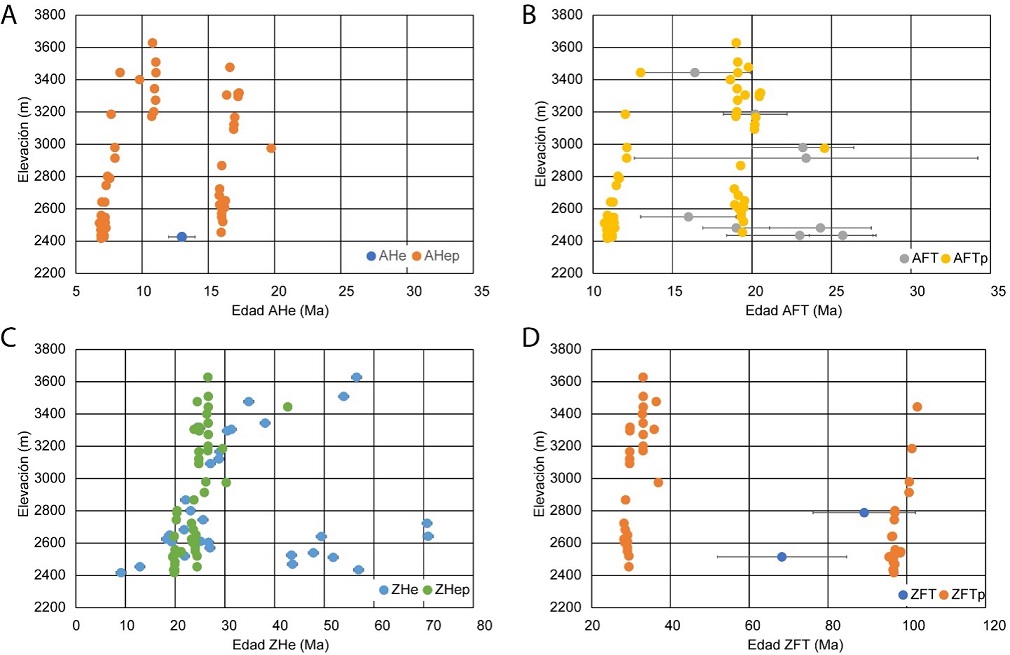
Figura 6 Comparación entre edades observadas y predichas(p) por el modelado termocinemático PECUBE para distintos sistemas termocronométricos: (A) AHe, (B) AFT, (C)ZHe, y (D) ZFT.
Mientras que las edades ZFT dependen del tiempo de ataque químico que se realice en el laboratorio para revelar las trazas de fisión confinadas. Adicionalmente, en esta investigación sólo se incluyeron las fallas de Boyacá y Soapaga, pero no se descarta la reactivación de otras fallas menores presentes en la zona de estudio.
Adicionalmente es importante considerar la acción de los fluidos hidrotermales los cuales pudieran afectar las edades obtenidas (Ehlers, 2005; Sueoka et al., 2019; Sánchez et al., 2020). Finalmente, en todos los modelados termocinemáticos inversos y directos realizados en esta investigación se asumió que la topografía estaba en equilibrio, es decir, que la topografía considerada al inicio y al final de los modelos siempre fue la misma. Esto último se hizo con la finalidad de analizar los tiempos y tasas de exhumación. Para los estudios de topografía se necesita una mayor densidad de edades observadas recolectadas a lo largo de la ondícula topografía (Bermúdez et al., 2011; Braun et al., 2012).
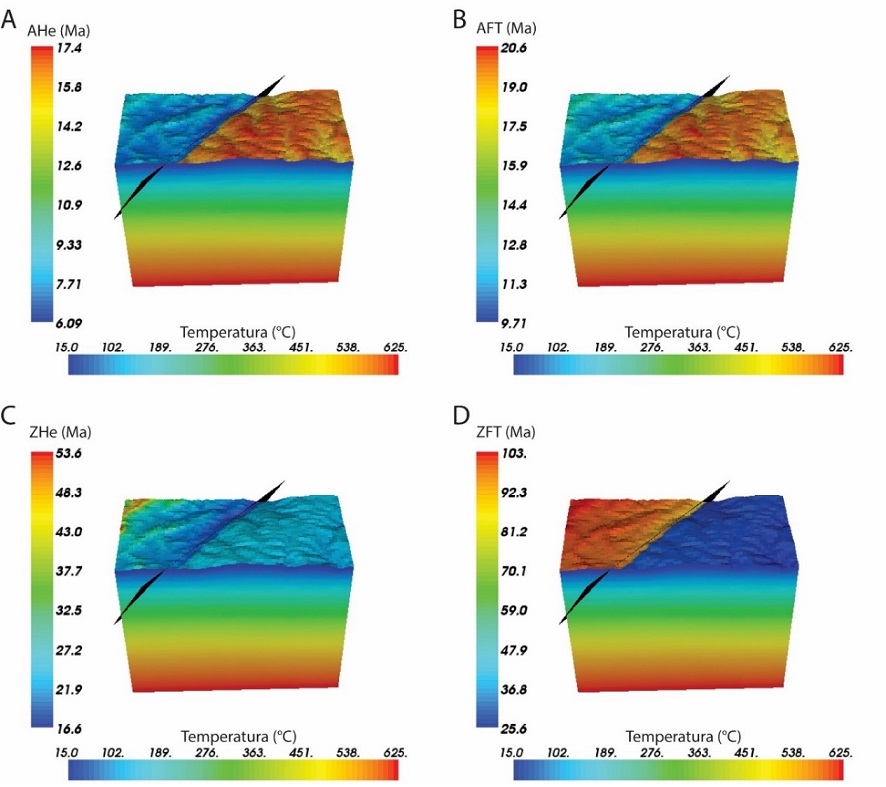
Las edades predichas por el modelo de menor misfit (denotado por asterisco en la figura 5) sobre cada píxel del MDE y el gradiente de temperaturas en profundidad pueden observarse en forma de diagrama tridimensional en la figura 7. En esta figura se observa que en el bloque yacente de la Falla de Soapaga el modelo predice las menores edades de ZFT y ZHe, lo cual se debe a que en este bloque la tasa de exhumación es mayor y mucho más reciente que para el bloque colgante. En contraste, las edades proporcionadas por los termocronómetros de más baja temperatura AHe y AFT tienden a ser más antiguos en el bloque yacente de la Falla de Soapaga (Figura 7), lo cual es concordante con los resultados mostrados en la figura 6.
4.2. VARIABLES SISMOLÓGICAS
Los valores a y b de la zona de estudio fueron derivados de la ecuación (4). Con el propósito de analizar anomalías en los valores de b, el área de estudio se dividió en cuatro cuadrantes y se calcularon para cada zona los valores de b. En la figura 8, se presentan las relaciones entre magnitud y frecuencia de la sismicidad reportada para el área de estudio (Figura 4) y el valor de b obtenido de la relación Gutenberg-Richter (Ecuación 4) para cada uno de los cuadrantes. En la figura 8, b11, b12, b21, y b22 son los valores de b obtenidos para cada uno de los cuadrantes c11, c12, c21, y c22, respectivamente, mostrados en la figura 4. El valor b observado está relacionado con la descripción de la cinemática de la falla en términos de deslizamientos, y su interpretación en términos de características intrínsecas de los mecanismos de fallamiento (Senatorski, 2020). Cómo se mencionó en la sección anterior, valores bajos de b corresponden a regiones de mayor tensión (Scholz, 1968; Nuannin et al. 2005; Wiemer y Schorlemmer, 2007). Sin embargo, considerando el error, los valores b para los primeros tres cuadrantes son muy homogéneos.
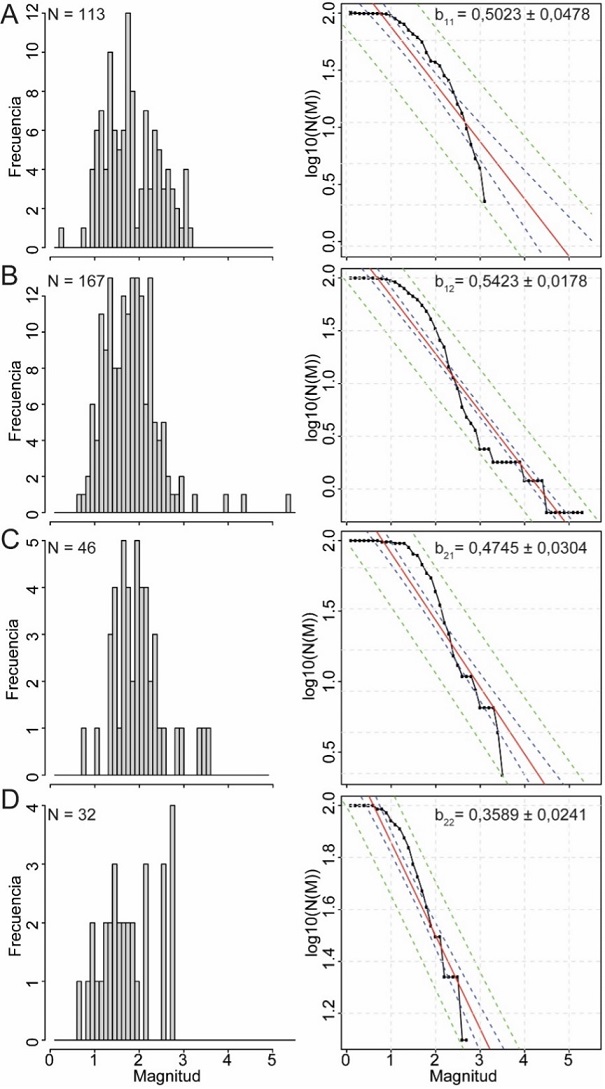
Figura 8 Relación magnitud-frecuencia de sismos reportados en el área y regresión por mínimos cuadrados para la obtención de los parámetros a y b necesarios para la derivación de la relación Gutenberg-Richter (Ecuación 4). Las líneas verde y azul representan las bandas de confiabilidad a 95 y 99%, respectivamente. (A) cuadrante inferior derecho (c11), N=113, (B) cuadrante superior derecho (c12), N=167, (C) cuadrante inferior izquierdo (c21), N =46 y (D), cuadrante superior izquierdo (c22), N=32. N representa el número de sismos de cada subzona.
Con el propósito de mostrar el comportamiento sísmico del área de estudio y la presencia de anomalías que puedan deberse a la complejidad geológica, se presenta en la figura 9 las distintas variables sísmicas calculadas a lo largo de la zona de estudio. Se observa en la figura 9A, la variación de los valores de b entre 0.3 a 0.6. Aquellas zonas donde se obtienen valores de b menores a 0.4 posiblemente se deba a que la cantidad de sismos reportados en el área es menor a 20 sismos. En esta figura se resaltan dos zonas, ambas situadas al este de la Falla de Soapaga, donde existe una importante convergencia de fallas menores (Mesalta, Cordizal, La Puerta, Tasco, Monchadita, Los Volcanes) que forman un sistema transpresivo local. Estas zonas coinciden con las áreas de mayor exhumación discriminadas en el modelado numérico termocinemático. En la figura 9B se presenta el mapa de energía sísmica acumulada en un radio de 2.5 kilómetros obtenido para el área de estudio, donde los valores oscilan de 237.8 a 116757.8 Joules. La deformación sísmica (Figura 9C) acumulada usando este mismo radio varía de 3.42E-19 a 2.84 E-15 s-1. El mayor valor de deformación sísmica se registra hacia el noreste de la Falla de Soapaga, en un área delimitada por las fallas de Soapaga, Paz de Río y Cordizal. La figura 9D representa el levantamiento sísmico acumulado en el área, el cual varía de unos pocos metros (5.8 m) a 107.4 metros, en una zona que experimenta un comportamiento de rumbo-dextral.
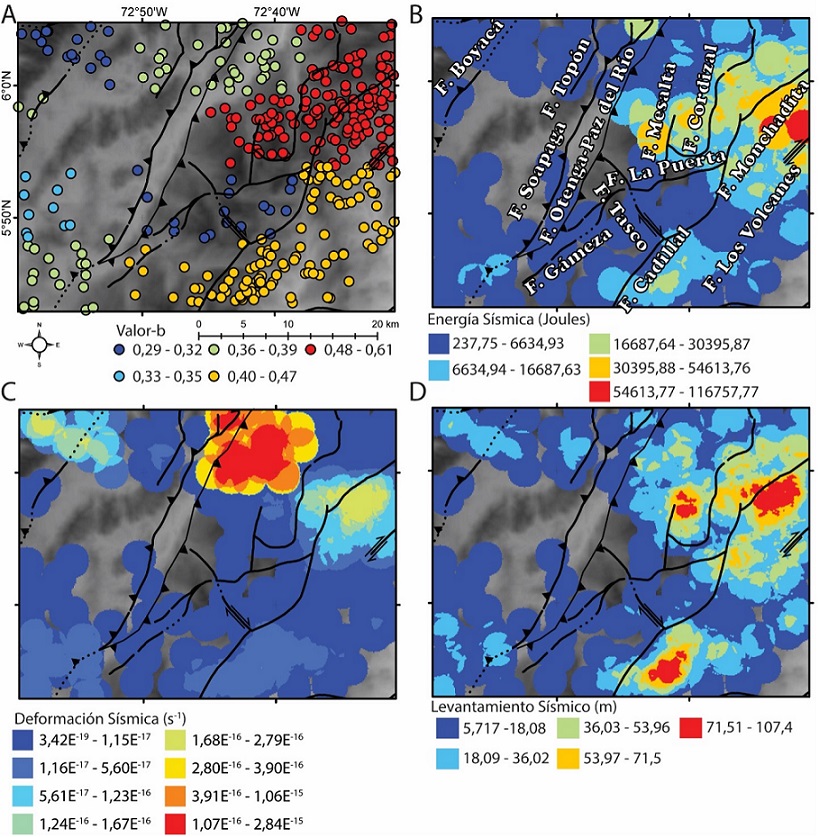
Figura 9 Comparación de diferentes parámetros sísmicos: (A) valor-b, (B) Energía sísmica acumulada desde 1993 al presente, (C) Deformación sísmica acumulada desde 1993 al presente, y (D) Levantamiento sísmico desde hace 5 Ma al presente. La cinemática de las fallas fue extraída de Ulloa et al. (1998).
4.3. VARIABLES GEOMORFOLÓGICAS
Las variables geomorfológicas como relieve (R), la integral hipsométrica (HI) y el índice de empinamiento (ksn), se calcularon para cada píxel del modelo de elevación digital, siendo posible elaborar mapas para cada una de estas variables, tal como se muestra en la figura 10. En el bloque colgante de la Falla de Boyacá, valores moderados de relieve y altos de HI sugieren un estado evolutivo del paisaje juvenil, donde la falla claramente ejerce un control topográfico fuerte.
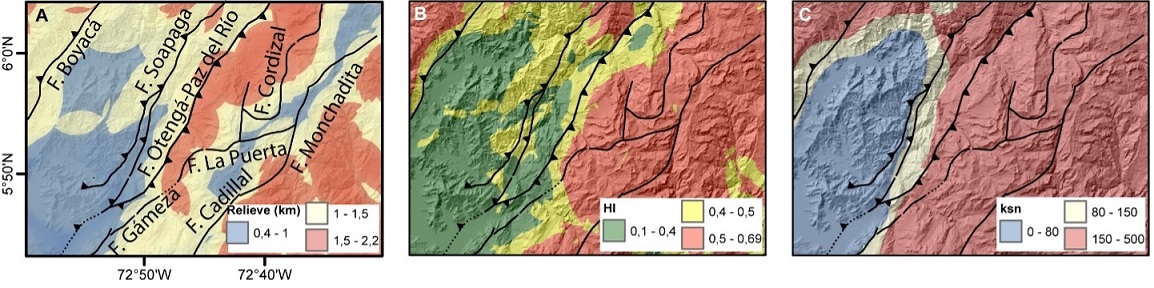
Figura 10 Métricas geomorfológicas: (A) Relieve local R, (B) índice hipsométrico HI y (C) índice de empinamiento ksn.
Esto se corroboró con los análisis del índice de empinamiento (ksn) ya que se observan valores altos de ksn relacionados a la Falla de Boyacá. En contraste, la Falla de Soapaga se caracteriza por valores moderados a bajos de relieve local, HI y ksn. Una posible explicación para este comportamiento puede ser la acumulación de grandes volúmenes de sedimentos cuaternarios que suavizan el paisaje. Para el caso del ksn, estos sedimentos modificarían la dinámica fluvial, inhibiendo la incisión de los drenajes. Otras dos explicaciones serían: i) la escala de tiempo estudiada con los índices (103 a 106 años), en la cual posiblemente esta estructura no ha tenido una actividad vertical importante, lo cual es compatible con los análisis de deformación sísmica (Figura 9) por lo que el paisaje no ha sufrido rejuvenecimientos recientes, y ii) existe una diferencia litológica importante entre los bloques yacentes y colgantes de la Falla de Soapaga (Figura 1). Explicar la contrastante dinámica erosional en ambas zonas es bastante compleja, por un lado se tiene las diferencias litológicas entre ambas zonas. Por otro lado, procesos exógenos diferentes podrían afectar de forma asimétrica los dos bloques, mientras en el bloque colgante el drenaje está limitado por las dos fallas principales, el drenaje del bloque yacente es mucho más amplio, y la distribución de la deformación sísmica por la presencia de fallas menores es mucho más compleja, donde estas estructuras (fallas Cordizal, La Puerta, etc; Figura 10), todas activas, pueden modificar el relieve y eso explicaría la diferencia en las medidas morfométricas.
5. Discusión
El modelo termocinemático de menor misfit sugiere un comportamiento diferencial en los patrones de exhumación a cada lado de la Falla de Soapaga, lo cual es observado en otros lugares de los Andes del Norte, específicamente, en los Andes de Mérida, donde el modelado termocinemático sugiere velocidades y tiempos de inicio de la exhumación diferentes (Bermúdez et al., 2011; Bermúdez et al., 2019). Mientras en el sector delimitado entre las fallas de Boyacá y Soapaga, la exhumación comienza más temprano, aproximadamente a 69.09 Ma con una tasa de 0.9 km/Ma, posteriormente a 15.73 Ma, esta tasa desciende a 0.2 km/Ma. En contraste, en el bloque colgante de la falla de Soapaga, la exhumación se detecta a partir de 22.65 Ma hasta el presente con una tasa de 0.5 km/Ma. Particularmente, en ese sector se identifican los mayores valores de levantamiento sísmico acumulado, el cual varía entre 71 a 107 metros (Figura 9D). Las edades AHe y AFT en el bloque yacente de la Falla Soapaga son relativamente más antiguas (17 a 20 Ma) que la zona situada al oeste con edades entre 6 a 9 Ma. Las edades y tasas de exhumación predichas para esta parte del bloque modelado son consistentes con las reportadas por varios autores a lo largo del Macizo de Santander y específicamente en localidades cercanas a la Falla de Bucaramanga (van der Lelij et al., 2016; Amaya et al., 2017, 2020). Esto indicaría que el sector más antiguo sufrió un importante rejuvenecimiento topográfico durante el Mioceno tardío. La pregunta que se deriva de esta observación sería: ¿a qué se debe tal rejuvenecimiento en el sitio de menor actividad tectónica de acuerdo con la sismicidad?. Diferentes autores (e.g., Mora et al., 2008; Ramírez-Arias et al., 2012), han favorecido la importancia del clima como agente controlador del relieve y las tasas de exhumación a lo largo de la Cordillera Oriental. Adicionalmente, investigaciones realizadas por Parra et al. (2009), Mora et al. (2010); Ramírez-Arias et al. (2012) y Silva et al. (2013), resaltan la importancia que ha tenido la inversión de la Falla de Boyacá para explicar los eventos de exhumación preandinos, al menos desde el Oligoceno hasta el Mioceno temprano. Los modelos termocinemáticos presentados acá confirman que esta falla es significativa desde el Cretácico superior (Maastrichtiense) hasta el Mioceno medio, a partir de cuando existe una fase importante de desaceleración en las tasas de exhumación que pudiera coincidir con eventos de enfriamientos lentos reportados por Mora et al. (2010) y Sánchez et al. (2012). Sin embargo, esto no es lo que se espera en zonas en donde los patrones de exhumación son controlados por el clima (Whipple et al., 2009; Hergarten y Kenkmann, 2019; Mishra et al., 2019).
Con el propósito de discriminar efectos tectónicos versus climáticos como agentes controladores del relieve o de la tasa de exhumación, se realizó la compilación de las distintas medidas calculadas en esta investigación, las cuales son resumidas en la tabla 3. Así, para facilitar la discusión de los resultados obtenidos y la integración con la pregunta antes mencionada, se hizo un análisis de correlación de Pearson para los valores reportados en la tabla 3.
Tabla 3 Diferentes variables obtenidas para aquellas locaciones donde existen datos de edades de trazas de fisión en apatito (AFT). En esta tabla: t es la edad AFT, 1s es el error sobre la edad, erAFT es la tasa de erosión calculada con Age2Edot (Brandon et al., 1998; Ehlers et al., 2005), HI es el valor de la integral hipsométrica, P es la precipitación, R es el relieve local, ES es la energía, DS es la deformación y LS es el levantamiento sísmico, respectivamente.
| Muestra | t | 1s | erAFT | HI | ksn | P | R | ES | DS | LS | Referencia |
|---|---|---|---|---|---|---|---|---|---|---|---|
| AM-09 | 25.7 | 2.1 | 0.3 | 0.4 | 69.9 | 815 | 597.0 | 1217.3 | 3.8E-18 | 1.2E-07 | Mora et al., 2010 |
| AM-10 | 19.0 | 2.1 | 0.4 | 0.4 | 55.9 | 815 | 718.0 | 1180.8 | 4.4E-18 | 1.4E-07 | Mora et al., 2010 |
| AM-12 | 16.0 | 3.0 | 0.4 | 0.3 | 20.2 | 907 | 749.0 | 1138.9 | 4.5E-18 | 1.4E-07 | Parra et al., 2009b |
| FT-583 | 23.2 | 3.2 | 0.3 | 0.4 | 377.4 | 349 | 1916.0 | 909.1 | 3.1E-16 | 9.4E-06 | Mora et al., 2010 |
| FT-571 | 23.4 | 10.8 | 0.3 | 0.4 | 371.8 | 745 | 1912.0 | 899.3 | 2.8E-16 | 8.5E-06 | Mora et al., 2010 |
| FT-627 | 20.2 | 2.0 | 0.3 | 0.6 | 260.9 | 335 | 1664.0 | 2915.5 | 6.7E-18 | 2.1E-07 | Mora et al., 2010 |
| A48 | 16.0 | 3.0 | 0.4 | 0.3 | 20.2 | 907 | 749.0 | 1138.9 | 4.5E-18 | 1.4E-07 | Silva et al., (2013) |
| A49 | 19.8 | 2.0 | 0.3 | 0.4 | 55.9 | 815 | 718.0 | 1180.8 | 4.4E-18 | 1.4E-07 | Silva et al., (2013) |
| A50 | 25.9 | 2.2 | 0.3 | 0.4 | 69.9 | 815 | 597.0 | 1217.3 | 3.8E-18 | 1.2E-07 | Silva et al., (2013) |
| FT2-04 | 16.4 | 3.5 | 0.4 | 0.6 | 157.2 | 624 | 1123.0 | 2393.7 | 3.1E-18 | 9.6E-08 | Ramírez-Arias et al., 2012 |
| AM-10 | 19.8 | 2.0 | 0.3 | 0.4 | 55.9 | 815 | 718.0 | 1180.8 | 4.4E-18 | 1.4E-07 | Ramírez-Arias et al., 2012 |
| COR1001 | 44.6 | 3.8 | 0.1 | 0.4 | 125.4 | 871 | 846.0 | 1168.6 | 1.9E-18 | 6.0E-08 | Silva et al., (2013) |
| COR1002 | 55.1 | 10.9 | 0.1 | 0.4 | 125.4 | 871 | 846.0 | 1132.7 | 1.9E-18 | 6.0E-08 | Silva et al., (2013) |
| COR1003 | 20.3 | 20.3 | 0.3 | 0.4 | 117.9 | 871 | 846.0 | 1142.4 | 2.0E-18 | 6.4E-08 | Silva et al., (2013) |
| COR1005 | 41.7 | 2.2 | 0.2 | 0.3 | 154.1 | 950 | 1031.0 | 1058.4 | 9.5E-19 | 3.0E-08 | Silva et al., (2013) |
| COR1006 | 12.2 | 4.3 | 0.6 | 0.3 | 154.1 | 971 | 1031.0 | 1306.1 | 9.4E-19 | 3.0E-08 | Silva et al., (2013) |
| AFT-270710-16 | 11.2 | 1.7 | 0.6 | 0.6 | 229.1 | 335 | 1616.0 | 2174.4 | 1.5E-17 | 4.6E-07 | Silva et al., (2013) |
La tabla 4, muestra los valores de los coeficientes de regresión de Pearson. La figura 11 representa la matriz de dispersión de las distintas variables mostrando gráficamente la relación entre ellas.
Tabla 4 Coeficientes de correlación de Pearson mostrando las relaciones entre las variables. Estas se consideran significativas a partir de un valor r ≥ 0.6. Las relaciones esperadas o "triviales" son resaltadas en letras itálicas.
| erAFT | HI | ksn | P | R | ES | DS | LS | |
|---|---|---|---|---|---|---|---|---|
| erAFT | 1 | |||||||
| HI | 0.34 | 1 | ||||||
| Ksn | -0.04 | 0.43 | 1 | |||||
| P | -0.23 | -0.82 | -0.68 | 1 | ||||
| R | 0.17 | 0.52 | 0.95 | -0.75 | 1 | |||
| ES | 0.36 | 0.88 | 0.22 | -0.64 | 0.33 | 1 | ||
| DS | -0.10 | 0.04 | 0.79 | -0.41 | 0.74 | -0.28 | 1 | |
| LS | -0.10 | 0.04 | 0.79 | -0.41 | 0.74 | -0.28 | 1.00 | 1 |
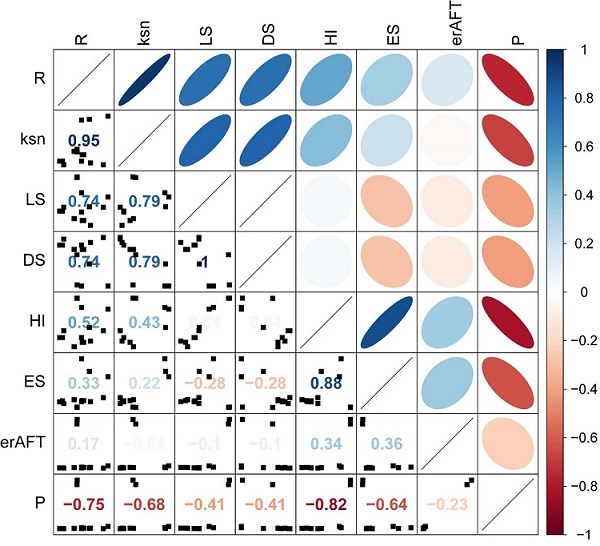
Figura 11 Matriz de dispersión mostrando las correlaciones entre las distintas variables: erAFT tasa de erosión a largo plazo derivada de los datos AFT, ES energía sísmica, HI integral hipsométrica, P precipitación, R es el relieve local, ksn índice de empinamiento, DS deformación sísmica y LS levantamiento sísmico. Las relaciones con mayor correlación están más cerca de la diagonal principal. Los colores debajo de esta última indican la fuerza de las correlaciones.
Considerando el índice HI, estos valores están relacionados con el grado de desequilibrio o equilibrio de las fuerzas erosivas y tectónicas sobre el relieve (Bustos et al., 2013). Aunque ésta no puede ser extrapolada a lo largo del tiempo geológico, ésta variable es muy útil en los estudios de tectónica activa, pudiendo así interpretarse como la relación que existe a corto plazo entre las fuerzas climáticas y/o tectónicas. Analizando la tabla 4 y la figura 10, se observa una correlación negativa (r=-0.82) entre HI y la precipitación promedio de la zona. En contraste, la relación entre HI y la energía sísmica es significativa (r=0.88). Sin embargo, un valor débil de correlación entre el relieve local (R) y HI (r=0.52), hace necesario que tales relaciones se estudien más detalladamente.
La correlación negativa entre P y R (r=-0.75) reafirma el hecho de que el clima no pareciera tener un factor preponderante en el área de estudio. Por el contrario, las fuerzas de las correlaciones (r=0.74) entre deformación sísmica (DS) y levantamiento sísmico (LS) desde hace 5 Ma, sugieren que la tectónica es el factor más importante como agente controlador del relieve. Estos resultados son consistentes con otros estudios realizados a lo largo de los Andes del Norte, y específicamente en los Andes de Mérida (Bermúdez et al., 2013), donde se encuentra un importante control tectónico sobre el relieve y sobre las tasas de exhumación a largo plazo. A diferencia del estudio antes mencionado, no se obtienen relaciones significativas entre las tasas de erosión calculadas asumiendo topografía en equilibrio con los parámetros sísmicos o climáticos, donde posiblemente la falta de correlación en este caso se deba a la posibilidad de que sea necesario incluir otros termocronómetros de baja temperatura como AHe. Sin embargo, esto no pudo realizarse ya que no existían datos suficientes en el área.
En regiones tectónicamente activas, como por ejemplo Taiwán, la actividad tectónica del cinturón se ha estudiado por diferentes métodos en varias escalas de tiempo (Chen et al., 2015). Sin embargo, las limitaciones de las características tectónicas en escalas de tiempo de 103 a 105 años son bastante limitadas. Así, para entender mejor el control tectónico sobre el relieve en esta escala de tiempo, los valores del índice ksn resultan muy útiles, por tal razón fueron incluidos en el análisis de correlación, obteniéndose relaciones significativas (r=0.95) entre este índice y el relieve (R), y entre deformación (DS) y levantamiento sísmico (LS) (r=0.79), los cuales son parámetros significativos a larga escala temporal.
Basados en la distribución espacial de los índices de relieve (R) y ksn (Figura 10), sumado a las fuertes correlaciones descritas (Figura 11; tabla 4), es importante resaltar que los predictores tectónicos (DS y LS) controlan el desarrollo del relieve y los procesos erosivos a corto plazo en la zona de estudio. Estos procesos erosivos pueden estar respondiendo al levantamiento de la superficie en escalas de tiempo relativamente recientes (103 a 106 años) y al parecer tienen un fuerte control estructural por las fallas con mejor expresión topográfica como la Falla de Boyacá. En contraste, la fuerte relación negativa (r=-0.68) refleja que el clima no pareciera ejercer un factor preponderante sobre el desarrollo del relieve (Figura 11).
6. Conclusiones
La modelización inversa termocinemática de datos termocronológicos tiene una serie de ventajas, ya que permitió discriminar el comportamiento asincrónico de la exhumación en un sector de la Cordillera Oriental hasta ahora poco estudiado. En el área de estudio, la Falla de Boyacá tiene una actividad tectónica significativa desde el Cretácico superior hasta el Mioceno medio, posiblemente durante el Mioceno medio cambia la cinemática de la falla, donde ese cambio trae como consecuencia el borrado parcial de los termocronómetros de baja temperatura.
En contraste, las edades y tasas de exhumación encontradas en el bloque yacente de la Falla de Soapaga son consistentes con las reportadas en la Falla de Bucaramanga. Además de esto, el análisis de los parámetros sísmicos como valores-b, energía, deformación y levantamiento sísmico, permitieron discriminar zonas con diferente comportamiento sísmico, bloque yacente de la Falla de Soapaga donde existe una importante coincidencia espacial entre las tasas de exhumación alta y levantamiento sísmico.
Adicionalmente, el estudio realizado permitió comprobar la importancia de la tectónica como un agente modelador del relieve observado en el área de estudio, la tectónica compresiva del área y la reactivación de fallas posiblemente se haya acelerado por la acreción de bloques a gran escala producto de la interacción de las Placas Nazca, Caribe y Suramérica.











 nueva página del texto (beta)
nueva página del texto (beta)