Introduction

Deoxyribonucleic acid, commonly known as DNA, is a large and complex molecule located in the nucleus of cells in all living organisms. It takes the shape of a double helix structure, where the genetic information unique to each individual and species is stored. All life is based on a code written in DNA molecule, the common denominator among living beings ^[1]. DNA can exist in a single-stranded form or as higher-order structures, including the canonical double helix and noncanonical duplex, triplex, and quadruplex species ^[2]. In a DNA molecule, each sugar in the two strands is attached to one of four nitrogenous bases - Adenine (A), Guanine (G), Cytosine (C), and Thymine (T). These bases can bond through hydrogen bonds, and their bonding possibilities differ. Specifically, DNA's double helix structure is attributed to hydrogen bonds between A-T (two) and C-G (three) base pairs^[3].

The number of hydrogen bonds determines the specific pairing between nitrogenous bases, but this structure is prone to errors and can sometimes be repaired ^{[4] [5]}.

According to the NCBI database ^[6], the number of records has doubled approximately every 18 months since 1982^[7]. From a computer science perspective, advanced metaheuristic strategies are required to handle such information^{[8] [9]}.

We developed a genetic algorithm to perform multiple genetic sequence alignments in this work. The objective is to explore the improvement from different parametrization schemas (Gp1, Gp2, Gp3, and Gp4) for the algorithm`s performance in terms of a) the solution quality (fitness) achieved by the algorithm and b) the computational effort (NF^E) with the count of evaluated functions. Since the parameter adjustment is made in the number of processing cores and mutation level, the secondary objective is to describe the impact of such adjustments on the processing time between the four algorithm schemas.

In the field of genetics, the parallelization strategy of processing information has shown significant improvement in the results, especially in reducing the computational time required to solve various problems^{[10] [11] [12]}. As a validation method, the numerical performance profile measures the relative efficiency of the algorithm in solving the set of problems^[13].

Bioinformatics software testing is often complex due to the difficulty in verifying the correctness of output and effectively generating failure-revealing test cases^[14]. In this work, we developed four strategies based on a genetic algorithm for the multiple sequence alignment problem and compared their performance to each other. Multiple sequence alignment (MSA) is essential in bioinformatics, aiding in phylogenetic, protein, and genomic analysis, but faces challenges in increasing alignment accuracy^[15].

There are several algorithm strategies in the state of the art, such as the "Progressive alignment," which has been one of the most used methods since the 1980s ^[16]. In addition to improvements in algorithm design, modern hardware technology has increased processing speed and enabled more simultaneous alignment sequences^[17]. Furthermore, integrations based on framework processing like Apache Spark can produce promising results and new perspectives ^[18].

Regarding the processing algorithms, researchers have developed exact, progressive, and iterative algorithms to address the Multiple Sequence Alignment (MSA) problem. Exact algorithms exhaustively search in the space of solutions and calculate the global optimum in sequences of relatively small lengths. However, they cannot guarantee finding the best solution in arrangements of hundreds or thousands of bases. Blast is an example of this type of algorithm ^[19]. On the other hand, progressive algorithms work by iteratively improving a sequence alignment by adding new sequences. The process involves gradually building upon an initial alignment until an optimal solution is found ^{[20] [21]}. Dynamic programming algorithms are commonly used to implement strategies that explore solution spaces using a substitution matrix ^[22]. One example is the ClustalW algorithm ^[23]. However, errors at the beginning of an alignment can propagate to the rest of the operation, which is a drawback of these algorithms. Furthermore, another strategy to tackle bigger MSA problems is to iteratively perform partial alignments ^{[24] [25]}.

On the other hand, Genetic algorithms are iterative metaheuristic strategies based on bioinspiration. A thorough analysis of the algorithms used in this context can be found in ^[26]. Due to the metaheuristic origin of Genetic Algorithms, which does not guarantee achieving the optimal solution, we assume no comparison between metaheuristics and/or stochastic strategies vs. progressive or deterministic strategies. However, metaheuristics permit working with more extensive problem instances.

This work presents a bioinformatics breakthrough and builds on fundamentals established by previous papers, such as ^[27], highlighting the importance of hardware acceleration in DNA sequence alignment. The utility of parallel processing was established by ^[28], which improves the process at the bit level. This work presents an innovative methodology that combines multiple techniques, including genetic algorithms, to enhance multiple sequence alignment. The methodology also employs the algorithms' performance profile as an efficient comparison method.

Due to the increasing scientific research in medicine-based informatics, the genetic algorithm has been tested using a set of genetic sequences from a group of vegetables of particular interest in medicine, such as Euphorbia pulcherrima, which has Anti-Inflammatory, Analgesic, Sedative, and Muscle-Relaxant Activities ^[29]. Preventing health complications is a significant motivation for studying the properties of vegetables.

Materials and methods

The computational processes in this study were meticulously developed on four identical personal computers (PCs) with a Microsoft Windows operating system. These PCs were equipped with 8 GB of RAM and an Intel core i5 processor, ensuring the study's robustness and reliability. The algorithms were programmed in Java with Netbeans IDE, a widely recognized and trusted platform for software development.

Proposed genetic algorithm: GAAPd

The algorithm starts with an Initial Population (Pi) of 500 individuals, which is later reduced to a fixed number of 100 individuals (Pt) between 100 generations. This helps maintain stability in the algorithm and prevents excessive computational resource usage. The individuals in the initial population are generated by random potential solutions to the problem.

Individuals are evaluated using a parallel process and the widely used Blosum evaluation matrix ^[36]. This matrix helps measure the quality of the in-turn alignment. There are ongoing efforts to parallelize genetic algorithms either partially or entirely, and these efforts have demonstrated meaningful results in their respective fields of application ^{[37] [38] [39] [40]}.

To speed up the evaluation process, we divide the workload and assign it to each evaluator instance, which is a component of the evaluation class designed for this process. We avoid double evaluations of union regions to ensure synchronicity among evaluators.

After completing the task, evaluators assign each population member a fitness value (ft) used on their partial results. Figure 1 illustrates the evaluation process described in this work.

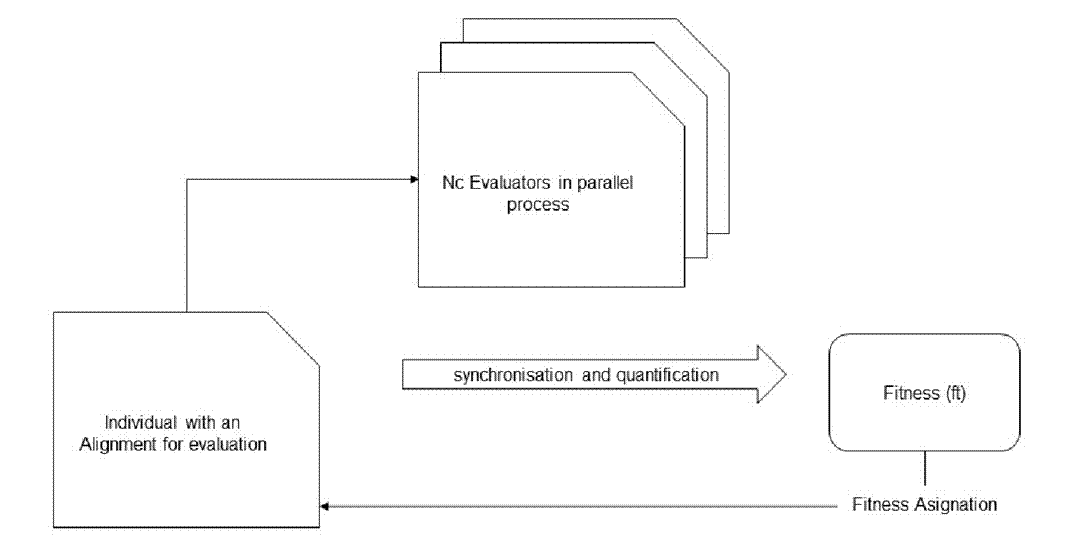
Figure 1 The process of evaluation. Nc refers to the number of evaluator instances created to evaluate everyone. Once the fitness value is assigned, the process is repeated for the following individuals in the population. 

According to theory, there is a direct correlation between the number of cores and the reduction of processing time (T^), stated in Equation (4). However, other intrinsic processes consume resources, such as synchronization and quantification.

T^=NF^E/Nc (4)

Where NF^E is the number of evaluated functions.

During the crossover process, individuals are randomly selected from the best performers of the evaluation process in the Pt set. In this context, it implies that only the most outstanding individuals proceed to the crossover phase. Their probability of being assigned to another individual is Pb= 1/Pt, equal for all.

A random double-point cut is made (CPA,CPB), and each crossover produces two children integrated into the population. The positions of CPA and CPB in the alignment matrix are also random.

After making the necessary cuts for both individuals, three parts of the father (P1F,P2F,and P3F) and three of the mothers (P1M,P2M,and P3M) are obtained.

Child 1 and Child 2 incorporate all six elements shown in Figure 2.

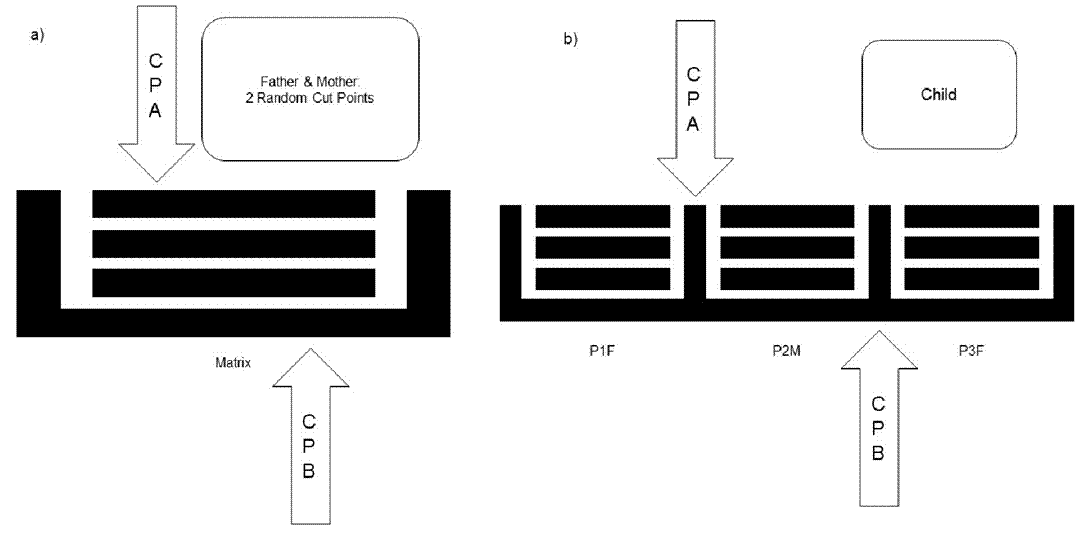
Figure 2 The crossover processes. In this process, two individuals produce three parts each. The resulting child has one part from the mother (P2M) and two from the father (P1F,P3F). Another child has one part from the mother and one from the father. 

The mutation process occurs for progenies ^[41], which is achieved by inserting or deleting gaps using the hyphen character "-" in various positions within the matrix. This process helps to improve the alignment further. The probability of an individual moving to the mutation process is Pm = 0.2, in which changes are randomly applied to the alignment matrix based on the Pm value.

Various mutation techniques have been documented in the literature, each relying on a specific mutation probability ^{[41] [42] [43]}. We developed four forms of mutation described as follows:

1. One of the sequences is randomly selected for mutation, where a maximum of 200 gaps can be inserted at the beginning.

2. A random point in the matrix is selected for gap insertion. The number of spaces added is randomly determined, up to 300.

3. Insertion of a gap column at a random point. A gap column is inserted at some position in the alignment matrix.

4. Random gaps are deleted. Up to 100 gaps are removed, and the number of gaps removed is randomly determined within a range of 1 to 100.

Results and discussion

The results of the fitness, NF^E, and time metrics are summarized and described below. As stated, the fitness value represents the algorithm's ability to reach better results, iteratively searching for solutions for a given problem. In this case, there are 13 problems for the performance evaluation; the problem count is presented in Table 3 as a C value. Furthermore, as described before, each problem C represents a set of sequences to be aligned in the multiple sequence alignment problem for the algorithm, and each algorithm (Gp1,Gp2,Gp3, and Gp4) ran 30 times for the calculated performance mean values. Also, the table presents the mean values for the fitness metric on each algorithm and each of the 13 multiple alignment problems.

The fitness metric shows promising performance results for the Gp2 and Gp3 algorithms since the objective is to increment the most possible fitness value. Also, the negative values describe complicated sequences for the alignment problem for all four algorithms.

For the number of evaluated functions (NF^E) metric, Table 4 shows the better performance of the Gp3 algorithm in problems 1 and 8. Gp1 performed better in sequence set number 2. Furthermore, all four algorithms present similar (NF^E) results in sequence set number 12. This shows a significant difference in the algorithms' performance in terms of the different strategies they represent.

The time it takes for the algorithms to process the stated problems is a commonly used metric for comparing the strategies' performance. Table 5 shows the performance in terms of the required time for each of the four algorithms to process the 13 multiple alignment problems. It is worth noting that Gp3 took more time than the other algorithms to process the alignment problems. Furthermore, Gp4 showed better performance than the different algorithms. The efficiency of an algorithm is not determined by the time it takes to run. Still, in this case, the time comparison helps show the main difference between the algorithms: the number of nuclei for the hardware process.

We present a Microsoft Excel file named results in the provided github link for a detailed description of the tables above.

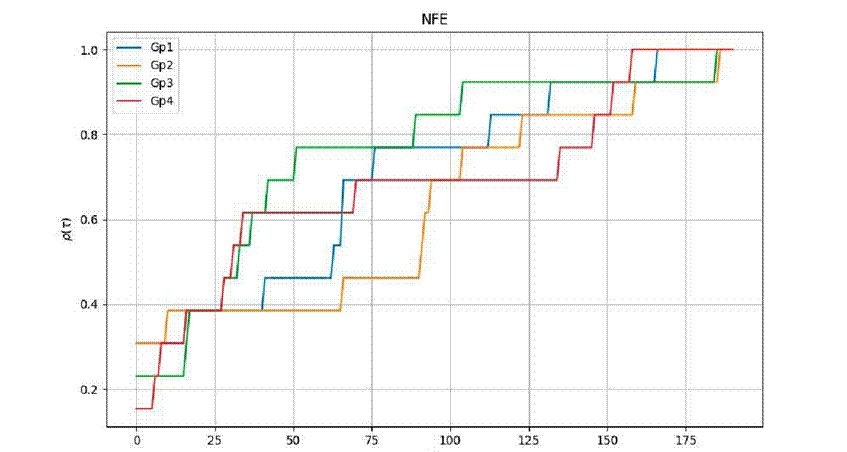
Figure 3 displays the performance profile for the metric tp,sd. This metric is associated with the ability of the algorithm to reach a better solution to a given problem. The Figure 3 shows the optimization method's ability to approach the global optimum in the problems considered. Gp1 and Gp3 maintain remarkable performance and approach convergence. This can be attributed to the fact that they perform single-core processing with maximum and minimum mutation levels of 1 and 4, respectively. It is worth noting that this characteristic is in Gp1 and Gp3 and contributes to the state of the art of genetic programming, particularly regarding the mutation level for the individuals in the Genetic Algorithms population. In other words, this means that the medium-level mutation had no fitness improvement benefits for this case study.

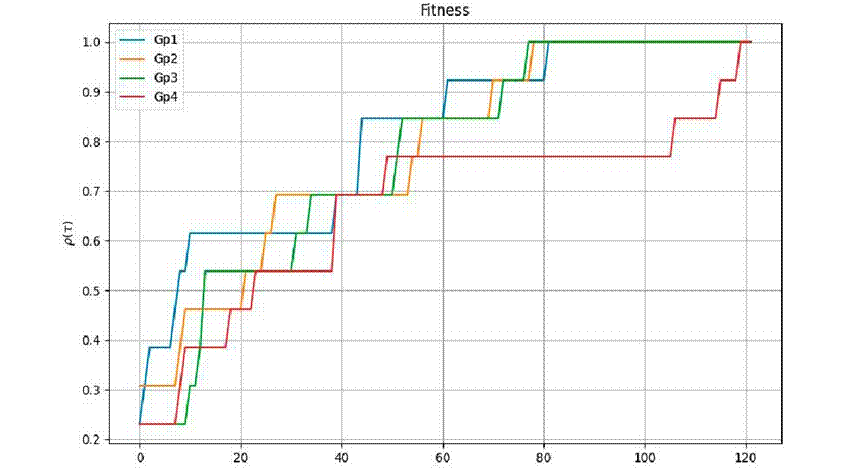
Figure 3 Numerical performance profile for fitness metric tp,sd described as fitness value for each of the four algorithms. 

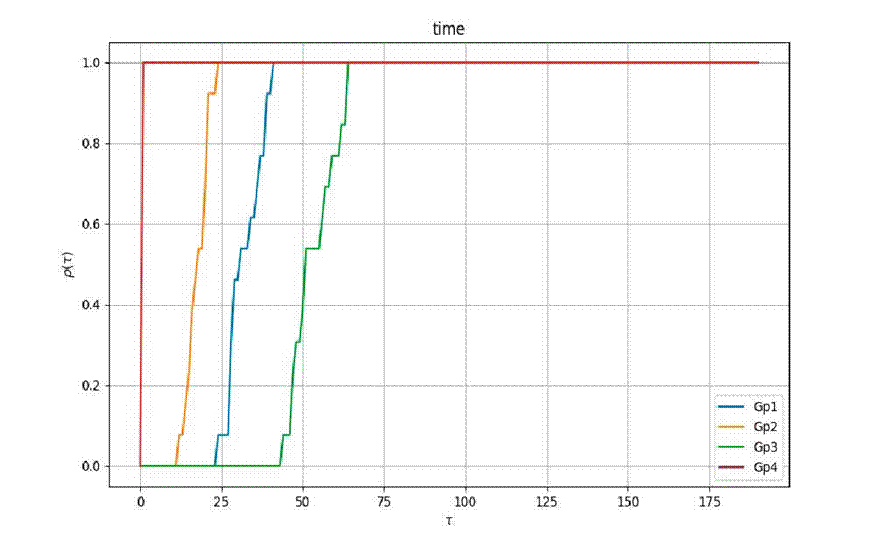
Regarding efficiency, the metric NF^E is associated with the number of evaluated functions and represents the hardware computational effort that the algorithmic strategy performs. Figure 4 is the performance profile, which indicates that Gp4 performs remarkably well. This may be because Gp4 employs the fewest mutations in the Genetic Algorithm and the highest number of cores in its algorithmic strategy. Similarly, Gp1 also demonstrates remarkable performance. It is worth noting that the previously described fitness results are consistent with the performance of Gp1 with its algorithmic strategy by using the fewest number of processing cores and the lowest level of mutation.

Figure 4 Numerical performance profile for the metric NF^E  

Figure 5 indicates that the Gp4 optimization method outperforms the others in terms of efficiency, as measured by the time spent on optimization T^. This may be because Gp4 utilizes greater parallel processing cores and fewer mutation processing than the other methods.

Figure 4 Numerical performance profile for the metric T^. 

However, the Gp4 algorithm did not produce remarkable fitness or NF^E values results. This shows that ensuring an efficient algorithmic and mutation process is more important than incorporating hardware resources.

Conclusions

This paper compares and discusses four strategies of the Genetic Algorithm method using the numerical performance profile model ^[47] in a set of genetic sequences. Based on the findings, the Gp1 approach is the most robust compared to other methods studied in this research. However, the efficiency, measured by the number of functions evaluated and convergence time, varies between the alignment methods. Gp4 is the method with the fewest evaluated functions and the highest processing speed. Thus, it can be concluded that the number of cores influences the alignment method's efficiency in parallel processing, and the robustness of the alignment method is related to the number of mutations. However, the Gp2 algorithm, with the highest core number and mutation level, did not perform remarkably well compared to the other strategies that varied the mutation level and number of cores.

Increasing the sequences in the data set is recommended to obtain more accurate results. By testing with the data set used in this research, these findings can be compared to other studies on genetic algorithms. Finally, it is essential to note that variations in mutation levels or other parameters can affect the performance of the different strategies.

On the other hand, conventional computer equipment can produce promising results when processing genetic information if the algorithms are specifically designed to make the most of hardware resources. Additionally, the computational effort of the hardware used impacts the number of evaluated functions. The quality of the solution obtained in the case of multiple sequence alignment relies on specific parameters of the genetic algorithm, such as the size of the population, the mutation level, and the crossing method. Moreover, the comparison method based on the determination of the performance profile is recommended as a valuable strategy for contrasting results in different metrics of interest.

Competing interests

The authors have no competing interests to declare.

Author contribution

E.R.W. conceptualization, methodology, software, writing original draft. M. M. D. S. formal analysis, investigation, supervision, validation, writing review and editing. J. V. S. validation.