2.1 USPEX calculations

USPEX employs an evolutionary algorithm to generate different structures of solid crystals, which is mostly unbiased because it only uses information that the researcher provides about the number and type of atoms to be contained within the crystalline unit cell ^{[17, 18, 19, 20]}. At first, the initial setof structures is generated by randomly choosing any crystal space group. Thus, this first generation is mainly composed of arbitrary far-of-equilibrium structures. It is then necessary to perform a structural relaxation to decrease and determine the total internal energy of each candidate system and use that value as a fitness criterion. Then, after a purely random start, new generations are created via genetic operations which can apply criteria such as heredity, mutation, and permutation; nevertheless, a portion of the new structures is still made randomly to ensure a level of diversity in each generation. The structural search ends when one of these criteria is achieved: no new best structure is generated for a certain number of generations, or, the set value for the maximum number of generations is reached.

Here, fixed composition searches were conducted to determine suitable high-pressure phases for solid fluorine. USPEX-based structure predictions were performed independently on different cell sizes, containing 2, 4, 6, 8, 12, and 16 atoms, in a pressure range spanning from 1.0 to 5.0 TPa in steps of 0.5 TPa, with the exception of 1.5 TPa that was not considered explicitly in this work but interpolated instead. Also, the two biggest cell sizes (12 and 16 atoms) were studied at four selected pressures instead of eight, and interpolated for the other pressures in that same range. The USPEX calculations started with an initial population of 30 structures, generated randomly with no restrictions on the space groups that could be assigned to the structures. In addition, no seeds or anti-seeds were considered. Subsequent generations were produced by applying the following variation operations (in parenthesis are the weights used in this work): heredity (50%), soft-mutation (15%), lattice mutation (10%), and permutation (5%), while the rest of the newly generated structures (20%) were still randomly produced with the random symmetric structure generator to assure diversity as explained earlier. We set the maximum number of generations to 50, and the convergence criterion was set to 20 repetitions of the same prediction. All USPEX calculations ended by reaching the repeated best structure convergence criterion.

2.2 DFT Calculations

The trial structures were optimized in a low-to-high precision process using first-principles DFT calculations using the Quantum Espresso suite ^{[21, 22]} for variable-cell relaxation. We increased the convergence criteria and precision settings at each step, with a reciprocal space resolution for k-point generation of 0.20, 0.16, and 0.12 π/Å, respectively. The k-point grids for the Brillouin zone integration were generated with the Monkhorst-Pack method ^[23]. Finally, all DFT calculations were performed using the plane-wave pseudopotential method with projector-augmented wave (PAW) pseudopotentials ^[24]. For the calculation of the exchange and correlation functionals, generalized gradient approximation (GGA) combined with Perdew-Burke-Ernzerhof (PBE) ^[25] parametrization was used. With the calculated lattice enthalpy after total relaxation, the structures were sorted from the lowest to the highest to be later used as input for the next generation.

3.1 Structural search process

In total, nearly 30000 fluorine structures with 2-16 atoms per unit cell spanning the pressure range of 1 to 5 TPa were generated in 40 different runs, via USPEX combined with DFT, using the Quantum ESPRESSO suite. As explained earlier, the first generation of each run consists of randomly generated structures. After that, the act of creating a new candidate structure usually follows a two-step procedure. First, the evolutionary algorithm enables the generation of a new system using one of three operations ^{[17, 18, 19, 20]}:

Each run contemplates the use of the genetic operations described above, together with a percentage of randomly generated structures. Figure 1 shows the enthalpy distribution of the generated systems within all 40 runs performed. We can see that randomly generated structures (yellow circles) with those from permutation operations (grey rhombus) and up to some extent also the ones from soft mutation (green dashes) span a large energy interval. In contrast, most relevant structures are created due to heredity (blue squares) and lattice mutation (orange triangles).

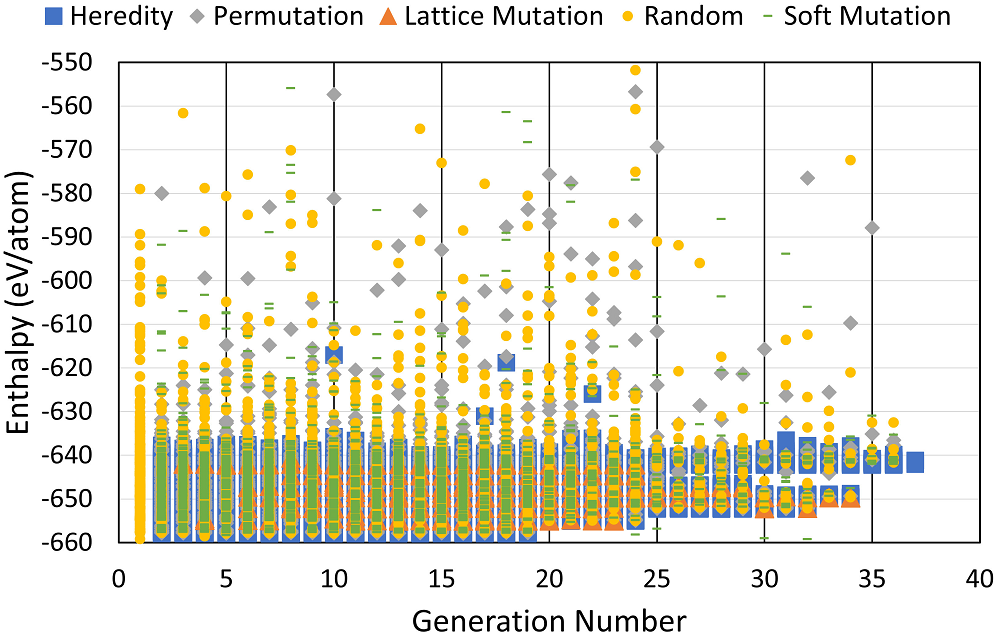
Figure 1 Enthalpy distribution, in eV per atom, of structures generated during 40 different runs for fluorine with 2-16 atoms per unit cell and at 1-5 TPa. The symbols represent the origin of generated structures: random generation (yellow circles) or as a result of certain genetic operations: heredity (blue squares), permutation (grey rhombus), lattice mutation (orange triangles), and soft mutation (green dash).  

3.2 Crystal structure determination

From USPEX predictions, 14 different crystal structures emerged as potential candidates for fluorine in the terapascal regime. These structures included all those previously reported that were compatible with our cell sizes (i.e., except for P6/mcc which contains 14 atoms per cell, since this size was not included in our study) and also a triclinic form. An additional closer inspection demonstrated that some phases were very similar to each other: in those cases the ones with lower symmetry were, in fact, slightly distorted cells of those with higher symmetry, with differences of around 1% in their cell parameters and atomic positions. This realization allowed us to narrow the list down to 9 structures: C2/m-2, Immm, I4/mmm, Fm3-m, C2/m-6, C2/c, Cmca, P42/mmc, and Pm3-n. More detailed calculations were carried out for the final set of structures. For instance, additional physical properties were calculated using Quantum ESPRESSO with a projector-augmented wave pseudopotential including seven valence electrons. For all final calculations, the kinetic energy cutoff for the plane-wave basis set was 200 Ry and their correspondent k-point grid for the Brillouin zone integration provided a total energy difference convergence of 2 meV per atom or better. The details are displayed in Table II.

Figure 2 shows the case of 8 atoms per cell at selected pressures after variable-cell optimization from ab initio results for the forces and cell stresses. USPEX was able to predict those phases proposed in previous works ^{[13, 15]} after just a few iterations. The insets show structures with the best individual enthalpy per atom at each generation; the squares mark the minimum enthalpy corresponding to different space groups:C2/c (red), Fmmm (brown), Cmca (orange), I4/mmm (blue), and Pm3-n (purple). Each green rhombus indicates the relative enthalpy of other structures obtained with USPEX and those reported in Refs. ^{[13, 15]} are in gray and pink circles, respectively.

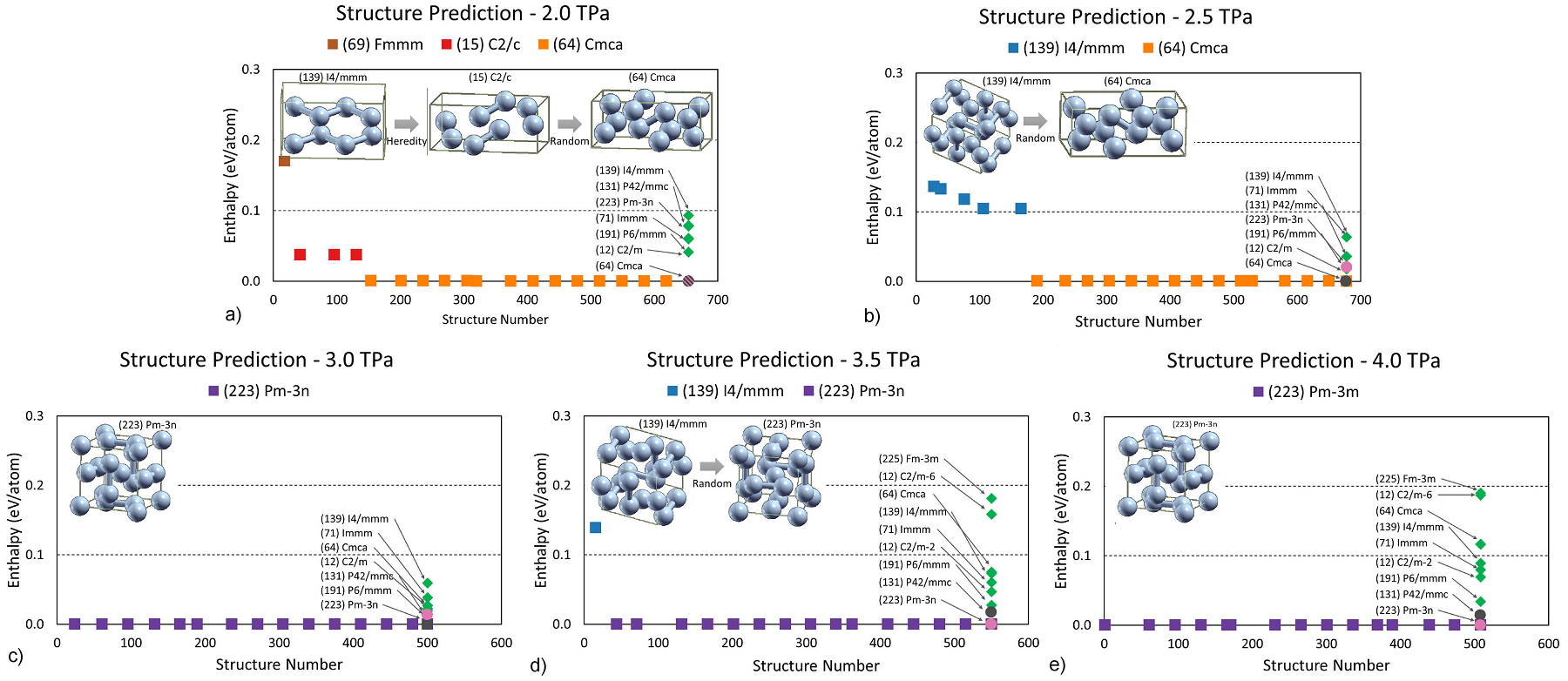
Figure 2 Structure prediction process for fluorine with 8 atoms per cell within the pressure range from 2.0 to 4.0 TPa. The squares show the lowest enthalpy obtained at a given generation, with the colors indicating the space group of the best individuals: C2/c (red), Fmmm (brown), Cmca (orange), I4/mmm (blue), and Pm3-n (purple). The insets show as 3D-images the sequences in the process of predicting the best structures by using the genetic algorithm implemented in USPEX. Relative enthalpies from Ref. ^{[13, 15]} are in gray and pink circles, respectively. 

Figure 3, the enthalpy relations for the structures found in this work, along with those previously proposed, are represented. The molecular phase Cmca remains stable up to 2.7(3) TPa. This persistence of the phase Cmca up to the terapascal regime was also reported in Ref. ^[15], and our USPEX calculations confirm that statement. Cmca transforms directly into Pm3-n, which was also reported as a stable form for solid fluorine by Olson et al.^[13] and Duan et al.^[15]. Nevertheless, in those two previous references the Pm3-m phase emerges at a higher pressure and after a reported intermediate phase: P42/mmc for Ref. ^[13] and P6/mmc for Ref. ^[15], which represent contradictory findings. In fact, our USPEX results found the phase P42/mmc (green line in Fig. 3) which shows an interesting tendency, but its enthalpy is not the lowest at any pressure within the range of our current study, although the situation could change at higher pressures. On the other hand, since the P6/mmc structure reported in Ref. ^[15] did not appear in the USPEX search because it has 14 atoms per cell, we included it manually in our calculations and its enthalpy is also plotted (violet line in Fig. 3). However, same as for P42/mmc, P6/mmc also does not become the most stable within our pressure range, therefore, our results do not support the findings from previous works regarding the existence of an intermediate phase between Cmca and Pm3-n at zero temperature.

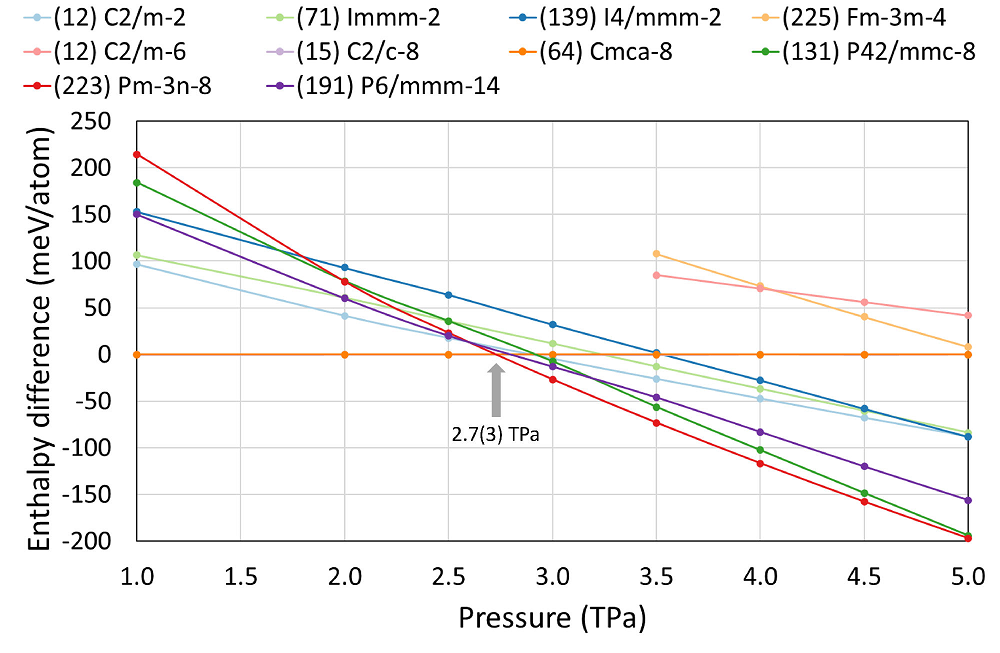
Figure 3 Enthalpy relations of the structures found with the USPEX code and those reported in Refs. ^{[13, 15]}, relative to the Cmca structure as a function of pressure. The final number after the dash, in the name of each structure, represents the number of atoms per conventional unit cell.  

Regarding the two most stable structures found in this work, we can conclude that Cmca is a molecular phase, since, for example at 1.0 TPa, the nearest F-F distance is calculated as 1.28 Å, and the second nearest F-F distance is 1.55 Å, which clearly establishes the molecular character of this crystalline structure which is shown in Fig. 4a). On the other hand, the phase Pm3-n is composed of two types of F atoms as shown in Fig. 4b): 75% of them (in gray) are polymer linear (1D) chains that go along the lattice vectors, and the remaining 25% (in yellow) are atoms located in the otherwise empty space between the linear chains, as shown in Fig. 4b). The mixed polymeric-atomic F character in phase Pm3-n is consistent with the reports from Refs. ^{[13, 15]}. At 4.0 TPa, the distance between atoms within the polymeric chain is 1.26Å, and the closest distance between an atom located in an interstice and an atom in a linear chain is 1.40Å.

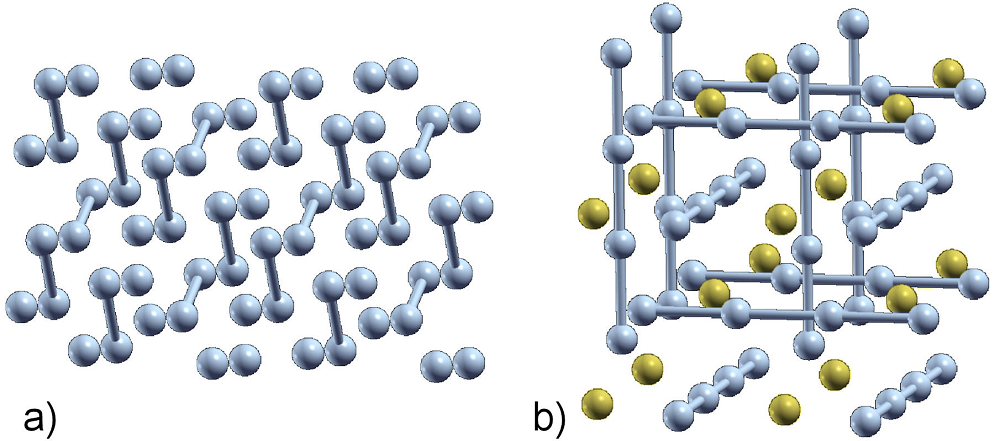
Figure 4 Fluorine primitive cell of a) molecular Cmca at 1.0 TPa, and b) polymeric-atomic Pm3-n at 4.0 TPa consisting of linear chains (gray spheres) and atoms residing in the voids between chains (yellow). 

The dynamical stability of structures Cmca and Pm3-n has been established through phonon calculations which demonstrate that they are stable as a function of pressure across the phase transition, as represented in Fig. 5. From a mechanical perspective, an observed increase in frequencies with increasing pressure shows that the phonon modes of phases Cmca and Pm3-n become stiffer, hinting to a more rigid structure. This observation is significant as it suggests that these structures are able to withstand increased stress and deformation without undergoing structural deformation or collapse.

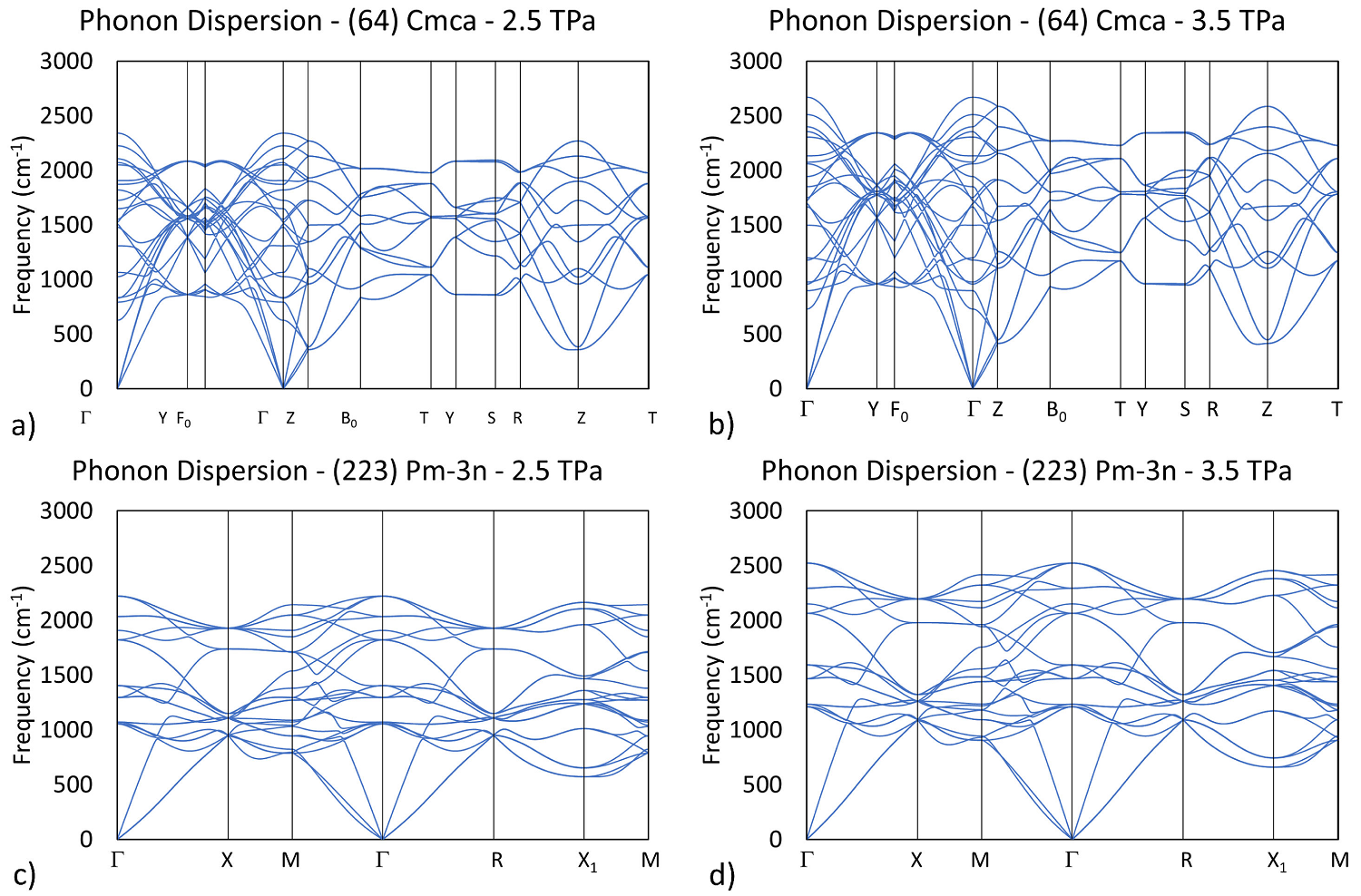
Figure 5 Phonon dispersion relations of Cmca at a) 2.5 TPa and b) 3.5 TPa, and Pm3-n c) 2.5 TPa and d) 3.5 TPa. 

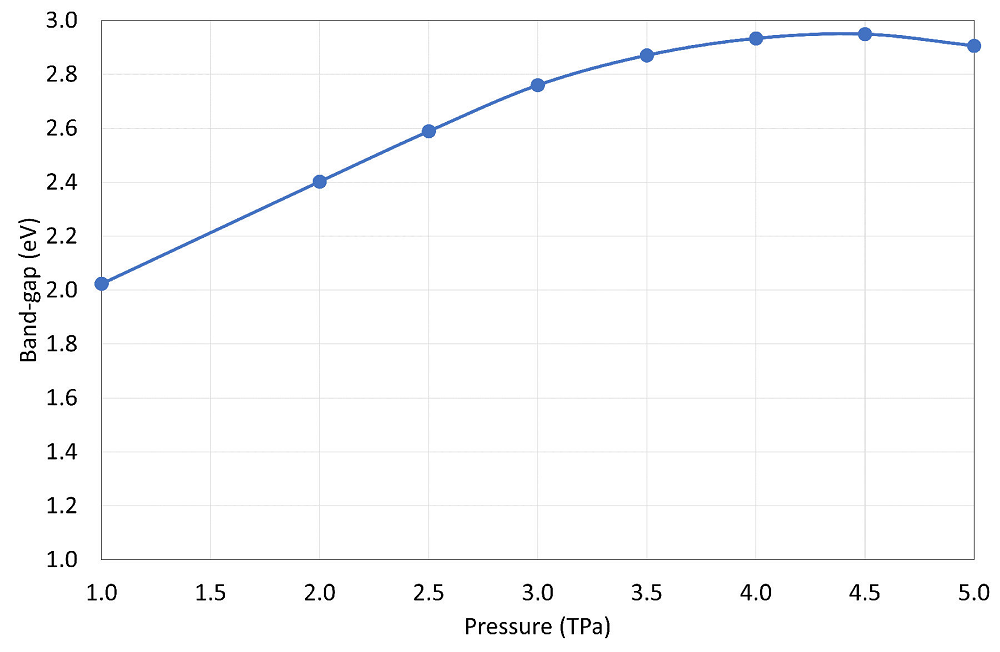
In addition to the phonon calculations, electronic band structures were also computed on both systems. At pressures below and above the transition, phase Pm3-n was found to be a metal according to an absence of gap at the Fermi level in its electronic band structure [Figs. 6c) and d)]. On the other hand, Cmca is a wide-gap semiconductor and our calculations revealed that at 2.5 TPa [Fig. 6a)] it has a band-gap of 2.6 eV which increases to 2.9 eV at 3.5 TPa [Fig. 6b)]. The behavior or this band-gap as a function of pressure is shown in Fig. 7 for the pressure range spanned in this study, showing an unusual behavior below 4.5 TPa, since, for most materials, applying pressure is a well known way to induce metallization, still, fluorine is not alone in this exotic behavior ^[26] where the ability to lower the energy by forming insulating closed-shell electronic structures wins over the tendency to lower the energy of the system by delocalizing the electrons. Finally, as expected, it is observed that the contributions to the total electronic density of states (DOS) for the two main phases in this study come primarily from the orbital p, rather than orbital s, however, while for the case of Pm3-n the projection on the orbital s is basically non-existing at energies that are close or above the Fermi energy, the contribution of that same orbital appears clearly also above the Fermi level for the case of Cmca, pointing to a sp-type of hybridization in that molecular phase.

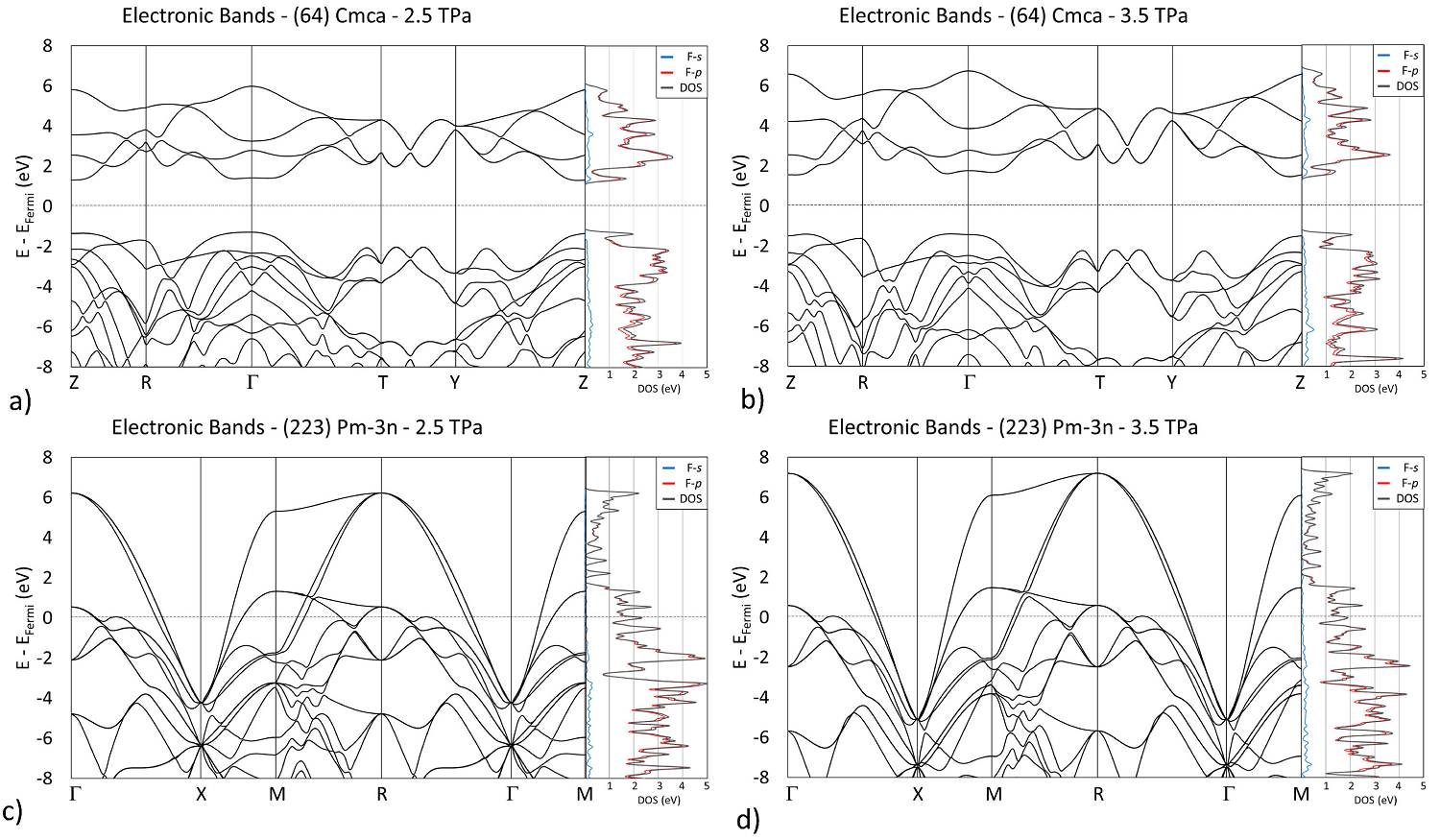
Figure 6 Band structure and partial density of states (PDOS) of Cmca at (a) 2.5 TPa and (b) 3.5 TPa, and Pm3-n (c) 2.5 TPa and (d) 3.5 TPa. The orbital s and orbital p contributions, and the total DOS are represented in blue, red, and gray lines, respectively. 

Figure 7 Variation of band-gaps for Cmca as a function of pressure.