First-principles investigation of the structural, electronic and optical properties of Zn2NbN3

Hassine, S.; Farkad, O.; Takassa, R.; Elfatouaki, F.; Choukri, O.; Ijdiyaou, Y.; Ibnouelghazi, E. A.; Abouelaoualim, D.; Hassine, S.; Farkad, O.; Takassa, R.; Elfatouaki, F.; Choukri, O.; Ijdiyaou, Y.; Ibnouelghazi, E. A.; Abouelaoualim, D.

doi:10.31349/revmexfis.69.041002

Servicios Personalizados

Revista

Articulo

Indicadores

Citado por SciELO
Accesos

Links relacionados

Similares en SciELO

Otros
Otros

Permalink

Revista mexicana de física

versión impresa ISSN 0035-001X

Rev. mex. fis. vol.69 no.4 México jul./ago. 2023 Epub 19-Nov-2024

https://doi.org/10.31349/revmexfis.69.041002

Material sciences

First-principles investigation of the structural, electronic and optical properties of Zn₂NbN₃

S. Hassine^a

O. Farkad^a

R. Takassa^a

F. Elfatouaki^a

O. Choukri^a

Y. Ijdiyaou^a

E. A. Ibnouelghazi^a

D. Abouelaoualim^a^*

^{^a} LaMEE, Department of Physics, Faculty of Sciences Semlalia, Cadi Ayyad University, P.O. Box 2390, 40000 Marrakech, Morocco.

ABSTRACT

An ab initio study using density functional theory (DFT) is carried out to explore the structural, electronic, and optical properties of Zn₂NbN₃ compound. The structural properties of this compound are determined by using the approximation (GGA-PBE) as implemented in WIEN2k. The calculated lattice parameters of the Zn₂NbN₃ compound are found to be a = 9.91 Å, b = 5.81 Å and c = 5.44 Å. The calculated electronic band structure and density of states indicate that the Zn₂NbN₃ compound is a wide gap semiconductor with a direct band gap of 2.5 eV. The different contributions of the electronic orbitals are discussed using the total and partial DOS with PBE and TB-mBJ approximations, which shows significant contributions from the Nb-d and N-p orbitals. The optical properties such as dielectric function, refractive index, absorption coefficient, and extinction coefficient are calculated and discussed.

Keywords: Zn₂NbN₃ ternary compound; Band structure; dielectric function; refractive index; density functional theory

1 Introduction

Since the 1990s, inorganic nitrides have attracted the interest of scientists for their chemical and physical properties beneficial for various industrial and technological fields ^[1]. Inorganic nitrides are divided into two categories according to their electronic properties: semiconductor wurtzite main group metal nitride and superconducting rocksalt transition metal (TM) nitride ^[2]. The first type such as AlN, GaN et InN present many important characteristics, including direct bandgap, high carrier mobility ^[1,3], they are largely used in laser diodes, solid states lighting, high data density optical storage media, radio frequency transistors ^[4, ^5]. The second type, such as TiN, VN and NbN, are employed in the hard coating, conduction barriers in semiconductor devices, and superconductors with transitions at a temperature around 20K ^[6, ^7]. Ternary nitride semiconductors are a large class of materials for a wide range of properties because of their unique nature and wide band gaps. Their intermediate bonding character due to the high energy of the nitrogen 2p orbital provides better hybridization with metal orbitals, making semiconductors crucial candidates in optoelectronic and photonic devices ^[8]. These materials have been widely studied in the past decade ^[9]. Principle calculations showed that various ternary zinc

nitrides exhibit electronic and optical properties. Using DFT calculations ^{Yoyo Hinuma et al. 2016}, investigated the electronic structure, stability and dopability of CaZn₂N₃ demonstrated tunable direct bandgap, light emission and harvesting. They have also proposed 21 interesting nitride systems, such as Ba₂ZnN₂ and Zn₂PN₃^[10]. Furthermore, ^{M. Mallmann et al. (2018)} have synthesized Mg₂PN₃ and Zn₂PN₃ ammonothermally ^[11] for the first time, and determined bandgap based on diffuse reflectance spectroscopy ^[12] , which estimated to be 5.0, 3.7 eV for Mg₂PN₃ and Zn₂PN₃ respectively. Afterwards, they performed DFT calculation to verify experimental values; both compounds crystallize in wurtzite (WZ)-type superstructure in orthorhombic space group Cmc2₁^[13]. In addition, ^{Zakutayev et al. 2021} have recently synthesized the Zn₂NbN₃ compound for the first time. Experimental results indicate that Zn₂NbN₃ crystallizes in cation-disordered WZ-derived cristal structure with 2.1 eV optical band gap and c/a=1.55 lattice constants ^[14]. In the same work, this group proved by theoritecal predictions an ordred structure of Zn₂NbN₃ with Cmc2₁ (space group 36) similar to Zn₂PN₃ and they demonstrated that it is energetically stable (formation energy equal to -0.52 eV/atom) ^[15]. In this work, we realized density function theory study as yet unreported to investigate structural, electronic and optical properties of Zn₂NbN₃ nitrides. The paper is organized as follow. In Sec. 2 the computational methods and the relevant technical details are described. Section 3 presents our results and discussion. Finally, a short summary and conclusion are given in Sec. 4.

2 Computational method

The calculations were performed via first-principles fullpotential linearized augmented plane-wave (FP-LAPW) method ^[16] in the framework DFT calculations as implemented in WIEN2K code ^[17, ^18]. For the exchangecorrelation energy functional, there are two approximations, the local density approximation (LDA) and the generalized gradient approximation (GGA). Realized that the LDA approximation is the most basic non-trivial approximation to the exchange-correlation energy. We assume that the energy XC of the system at a given point is equal to the energy of a homogeneous electron gas with (approximately) the same density at that point. However, we run into problems when describing systems with widely varying electron densities ^[19, ^20]. In our calculation, we used the generalized gradient approximation (GGA) in the Perdew-Burke-Ernzerhof (PBE) form instead of the LDA. Therefore, GGA is a class of functions that consider the density at a given point and the density’s gradient (variation), allowing it to describe systems (to some extent) better. GGA has become a common denominator in many studies, especially when describing large-scale systems with different atoms ^[21]. In addition, the GGA-PBE approximation provides accurate results for the structural and electronic properties of semiconductors ^[22, ^23]. For the band gap calculations with accuracy, we perform GGA with the addition of Tran-Blaha modified Becke-Johnson (TB-mBJ) exchange potential ^[22- ^25]. The details of the calculations are as follow: The muffin tin radius sphere (Rmt) for each atom Zn (2.05), Nb (1.90) and N (1.63). All the crystal structure and the atomic coordinates are fully relaxed using the PORT method until the force on each atom converges to less than two mRy/u.a. The maximum angular momentum of the atomic orbital basis functions was set to lmax=6. We expand the basis function up to Rmt×Kmax=7, where Rmt denotes the smallest atomic sphere radius and Kmax denotes the largest k vector in the plane wave expansion. The Fourier expansion charge density is truncated at Gmax=12Ry1/2. The total number of k-points in the first Brillouin zone (BZ) was determined equal to 1000, and the k-point mesh was 10×10×9. The iteration process stopped at a total energy convergence threshold unless 0.01 mRy.

3 Results and discussion

3.1 Structural properties

In our work, we report Zn₂NbN₃ wurtzite derived orthorhombic structure with Cmc2₁ (space group 36). In order to obtain the most stable structure, we optimized the structure by calculating different energies for different volumes using GGA-PBE adapting to the Murnaghan equation Eq. (1). The E(V) diagram is shown in Fig. 1b). The stable Zn₂NbN₃ wurtzite derived orthorhombic crystal with the ordered occupation of Zn and Nb by cationic sites is shown in Fig. 1a) and relaxed lattice parameters are grouped in Table I as well as the previous theoretical and experimental results.

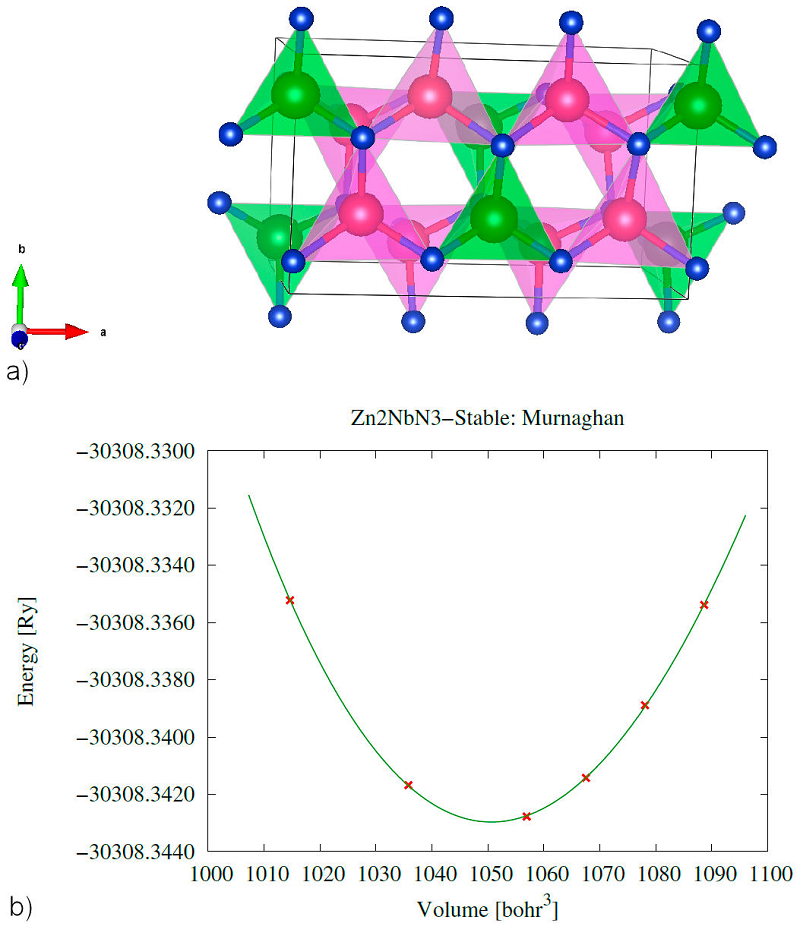
E(V)=E0+K0V01K'0(K'0-1)(VV0)1-K'0+1K'0VV0-1K'0-1. (1)

Figure 1 Zn₂NbN₃ structure optimization a) Zn₂NbN₃ relaxed structure with atom’s color are Zn (magenta), Nb (green), and N (blue) and b) diagram of energy versus volume.

Table I Relaxed lattice parameters of Zn₂NbN₃.

Lattice parameters	PBE	Other Theoretical works [14]	Experiment work [14]
space group	Cmc2₁	Cmc2₁	P63mc
crystal system	orthorhombic	orthorhombic	Hexagonal
a (Å)	9.91	9.852	3.36
b (Å)	5.81	5.782	3.36
c (Å)	5.44	5.386	5.26
Cation’s ordre	ordered	ordered	disordered

The thermodynamic stability of Zn₂NbN₃ was studied by the formation energy, which is described as the difference between the total energy of final products and these of reactants ^[26, ^27]. After relaxation, high-precision static calculations were performed to calculate the precise ground state energies of the reactants and product in order to compute the formation energy per atom of Zn₂NbN₃ using the following equation:

ΔEf=EZn2NbN3tot-αE(Zn)-βE(Nb)-γ2E(N2), (2)

where EZn2NbN3tot is the total energy per formula unit of the compound Zn₂NbN₃ under the equilibrium lattice constant, and E(Zn), E(Nb), and E(N2) are the ground-state energies of zinc (space group: 225 (Fm-3m)), niobium (space group: 225 (Fm-3m)), and nitrogen dimers (space group (225 (Fm- 3m)), respectively. Generally, the better the structural stability, the more negative the formation energy value. In our case, the formation energy of Zn₂NbN₃ is -0.50 eV/atom, which means that our compound under study is thermodynamically stable; this value confirms other theoretical studies (DEf (Zn₂Nb₃N) = -0.52 eV/atom) ^[15].

3.2 Electronic properties

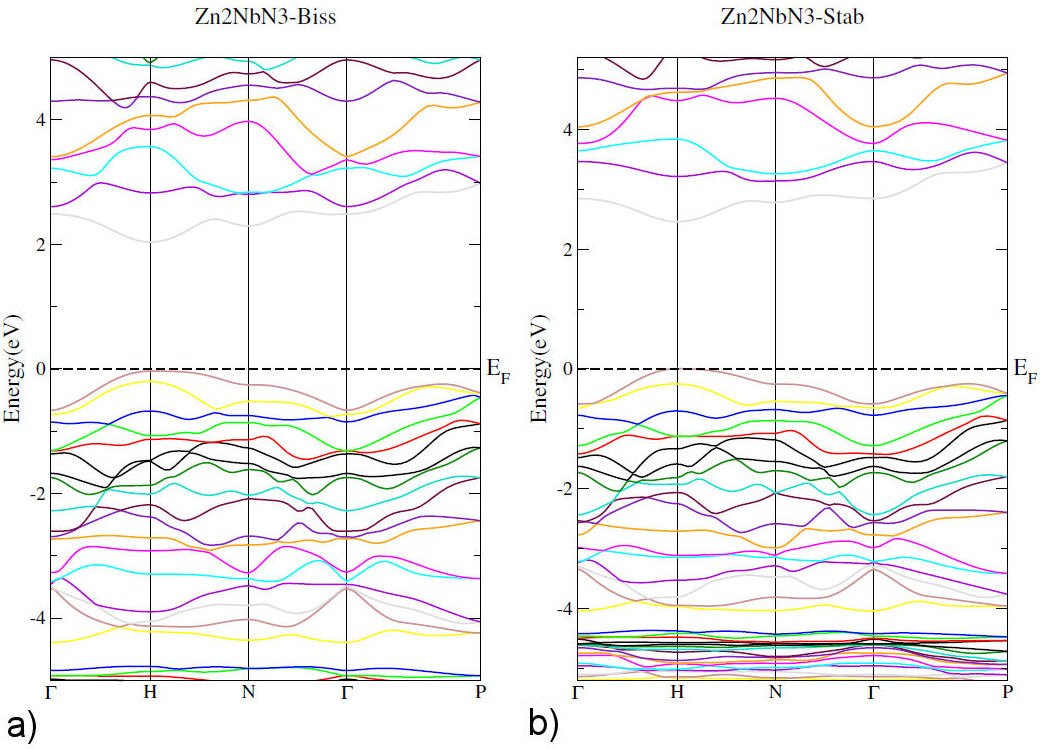
The gap is one of the most important electronic parameters that allow us to get very useful informations about the nature, efficiency, usefulness of the material ^[22]. The exact bandgap of semiconductors are very appreciable for their efficient use in optoelectronic and other electronic devices, and minimal variation of its value induces significant changes in application devices ^[28]. In our study’s calculations, the electronic bandgap of Zn₂NbN₃ is determined using (PBE) and (TB-mBJ). The results are shown in Table II.

Table II Different gaps of Zn₂NbN₃ compound.

Gap	PBE	TB-mBJ	Other works [14]
Zn₂NbN₃	2 eV	2.5 eV	3.5 - 3.6 eV

Figure 2 illustrates band structure of Zn₂NbN₃. We noticed that it is characterized by a direct bandgap with clear semiconducting behavior. Valence band is close to Fermi level, while conduction band do not. We can see that the maximum of valence band and the minimum of conduction band are located at the H point with a value of bandgap about 2 eV and 2.5 eV using (GGA-PBE) and (TB-mBJ) approximations, respectively.

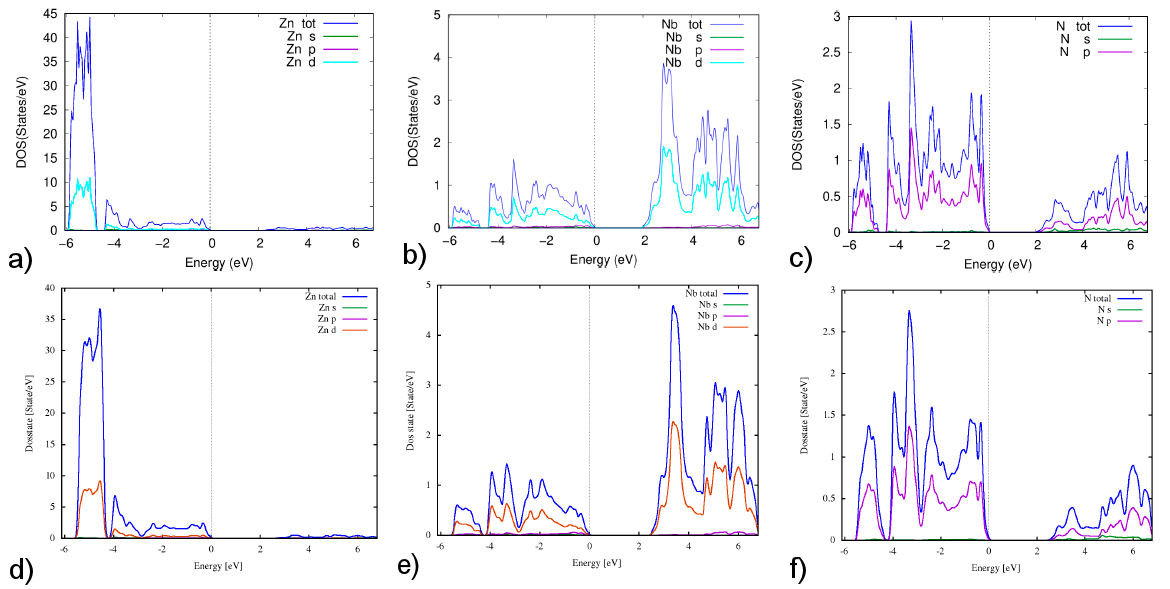
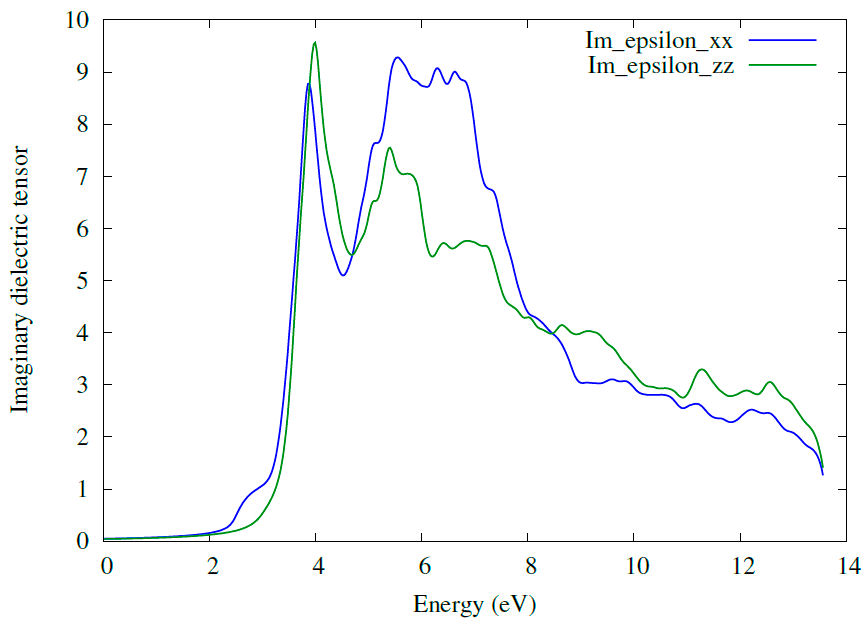
Figure 2 Band structure of Zn₂NbN₃ compound, a)GGA-PBE approximation and b)TB-mBJ approximation.

On the other hand, the total density of states (DOS) and the partial DOS play an essential role in investigating the electronic properties of the compounds. In Figs. 3 and 4 show the total DOS and partial DOS of Zn₂NbN₃ structure and Zn, Nb, and N atoms, respectively, calculated with the two potentials PBE and TB-mBJ. As shown in Fig. 3, the total DOS plot shows a zero-gap at the Fermi level with the two used potentials, confirming the semiconducting behavior in the electronic band structure plot. The total DOS simulated with PBE and TB-mBJ potentials is almost the character of the Zn atom, especially of d orbital in the energy range between -4.5 and -6 eV in the valence band [Fig. 4a) and 4d)]. The energy range -4.5 to 0 eV is dominated by Znd, Nb-d, and N-p orbitals [Figs. 4a) to 4f) respectively], indicating a strong interaction between these atoms. We can also see at the energy interval close to the Fermi level that the main contribution comes from the N-p orbital [Fig. 4c) and 4f)]. In the conduction band, the DFT calculations with the two potentials PBE and TB-mBJ indicate that the main contribution is from Nb-d and N-p orbitals [Figs. 4b), 4c), 4e) and 4f) respectively] with the domination of Nb-d orbital indicating a strong interaction between Nb and N atoms.

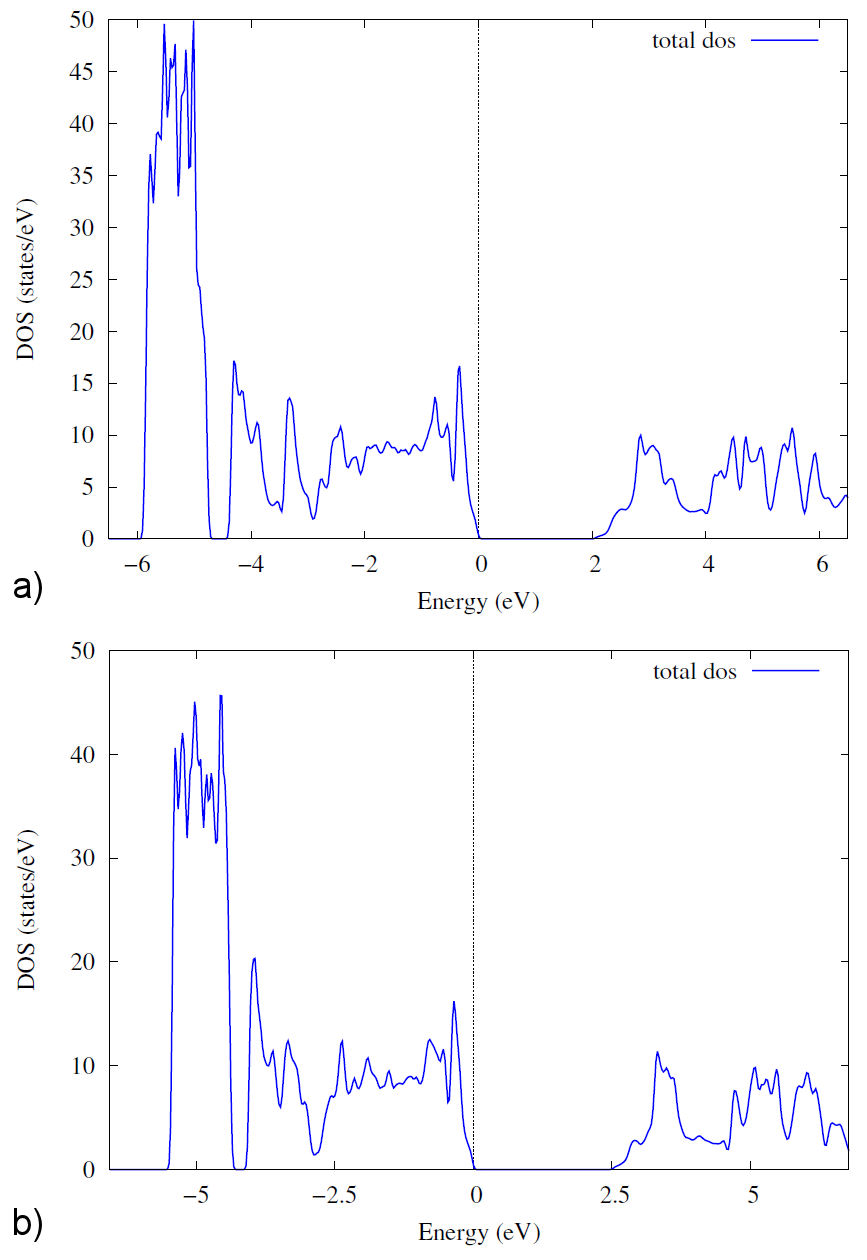
Figure 3 The total density of States of Zn₂NbN₃ compound with both approximations GGA-PBE and TB-mBJ. a) GGA-PBE approximation, and b) TB-mBJ approximation.

Figure 4 Total and partial DOS with PBE and TB-mBJ approximations of Zn a), d), Nb b), e) and N c), f), atoms respectivelly.

3.3 Optical properties

The optical properties of a material describe its response to electromagnetic radiation. A detailed optical characterization is thus conducted to determine the optoelectronic nature of of Zn₂NbN₃, using the TB-mBJ approximation and thus support their use in the fabrication of optoelectronic devices.

3.3.1 Dielectric function

The optical properties of any material explain the frequency response to the energy of the incident photon (E=hν). Because the frequency depends on the dielectric function, we can use the latter to determine different optical parameters using the relation that expresses complex dielectric function ^[29]:

ε(ω)=ε1(ω)+iε2(ω), (3)

where ε1(ω) is the real part that helps to determine the polarization and dispersion of light, while ε2(ω) is the imaginary part that describes the absorptive properties of the material. The two parts of the complex dielectric function ε1(ω) and ε2(ω) are related by the Kramers - Kronig relation. Optical properties depend strongly on the imaginary part of dielectric function ε2(ω), which can be calculated using the following relation ^[30].

ε2(ω)=8πeωm∑n‍∑n'‍∫‍|Pnn'v(k)2|fkn(1-fk'n)δ(Enk-En'k-ℏω)dk3(2π)3, (4)

where Pnn'v(k) is the projection of elements of momentum dipole matrix along direction v of electric field between final and initial stages. fkn is Fermi-Dirac distribution, and Enk is the energy of one electron.

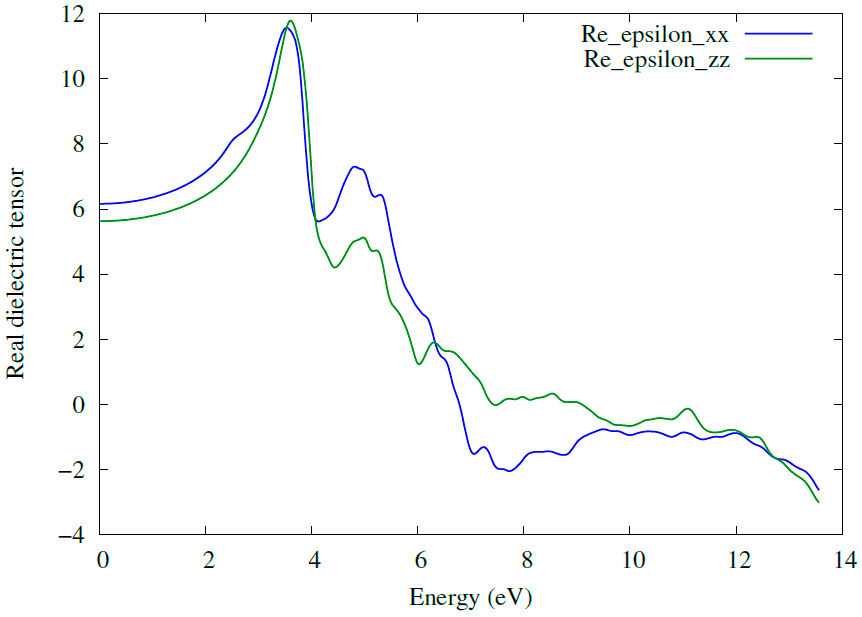
The Kramers-Kronig method can help us to extract the expression of the real part of the dielectric function ε1(ω) using the imaginary part of dielectric function ε2(ω) ^[31].

ε1ω=12πP∫0∞ω'ε2ω'ω'2-ω2dω' (5)

Optical properties were computed using dielectric coefficient values. The real part of the dielectric function shows the ability of a material to respond to the incident electromagnetic wave. The knowledge of both real and imaginary parts of the dielectric function allows the calculation of important optical functions; the static value of real part ε1(0) is obtained on the vertical axis of the plot shown in Fig. 5 approximately 6.1 in xx direction 5.7 in zz direction. The real part of the dielectric function becomes negative at approximately 6.9 and 9.5 with high incident energy having anisotropy between xx and zz directions which shows reflectivity for photons for our considered compound Zn₂NbN₃. We can characterize electronic properties with the help of an imaginary part of dielectric function related to absorption phenomenon ^[32], the peaks in the spectra of the imaginary part of dielectric function describe transitions of electrons from the valence to conduction band ^[33]. Calculated spectra of imaginary part of dielectric function ε2(ω) for Zn₂NbN₃ is shown in Fig. 6, the maximum value of ε2(ω) located at 4 eV. The electronic band structure shows a direct bandgap; therefore, direct optical transitions occur between universal localized in the highest valence band (VBM) and the lowest conduction band (CBM). the main peaks in ε2(ω) are due to interband electronic transitions from occupied N- 2p states localized in the VBM to the unoccupied Nb-4d states localized in the CBM (N-Nb bond) [Figs. 4e), 4f)]. It can be seen in the xx direction three intense peaks close to 9 in the UV region (5-7 eV); however, in the zz direction, there is one intense peak (7) at 5.5 eV; all of these features are attributed to interband transitions from occupied Zn-3d states localized in the highest valence band to the unoccupied Nb - 4d states localized in the lowest conduction band (Zn-Nb bond) Figs. 4d), 4f).

Figure 5 Real part of dielectric function of Zn₂NbN₃.

Figure 6 Imaginary part of dielectric function of Zn₂NbN₃.

3.3.2 Absorption coefficient

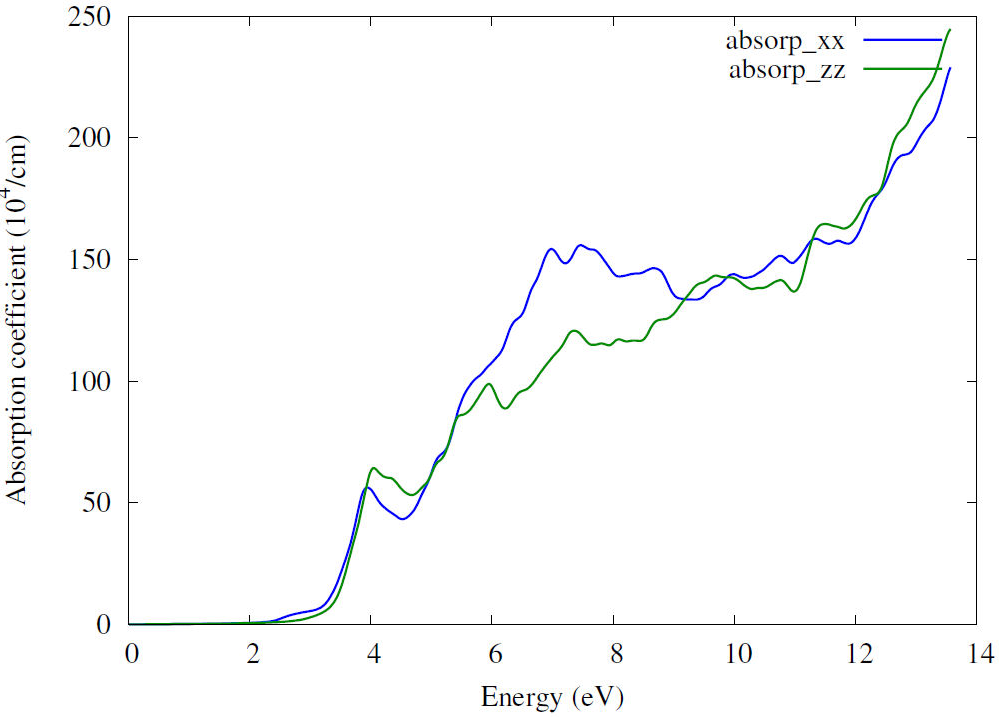
The reason for a transition of an electron from the valence band to the conduction band is the interaction between incident photon and electron, which is related to absorption coefficient ^[34]. Figure 7 shows spectra of absorption coefficient. Calculations show that our compound possesses transparent behavior below the energy band gap (valance band) because the incident photon’s energy is insufficient to transport electrons from the valance band to the conduction band. The first peak in the plot occurs at 4.04 eV with a value of optical gap estimated to be 3.1 eV. The second appears at 7.3 eV. After that, we notice a growth of the absorption with high energies indicating an effective optical behavior ^[33]. The appearance of the absorption beyond the energy 3.1 eV means that the absorption in semiconductors occurs when the incident energy exceeds the energy gap. In addition, strong absorption in the ultraviolet region suggests that Zn₂NbN₃ could be used in UV light protection ^[35].

Figure 7 Absorption coefficient plot of Zn₂NbN₃.

3.3.3 Refractive index

Refractive index can be calculated using the relation bellow with the help of real and imaginary part of dielectric function ε1(ω) and ε2(ω) ^[29].

n(ω)=ε12(ω)+ε22(ω)2+ε1(ω)2. (6)

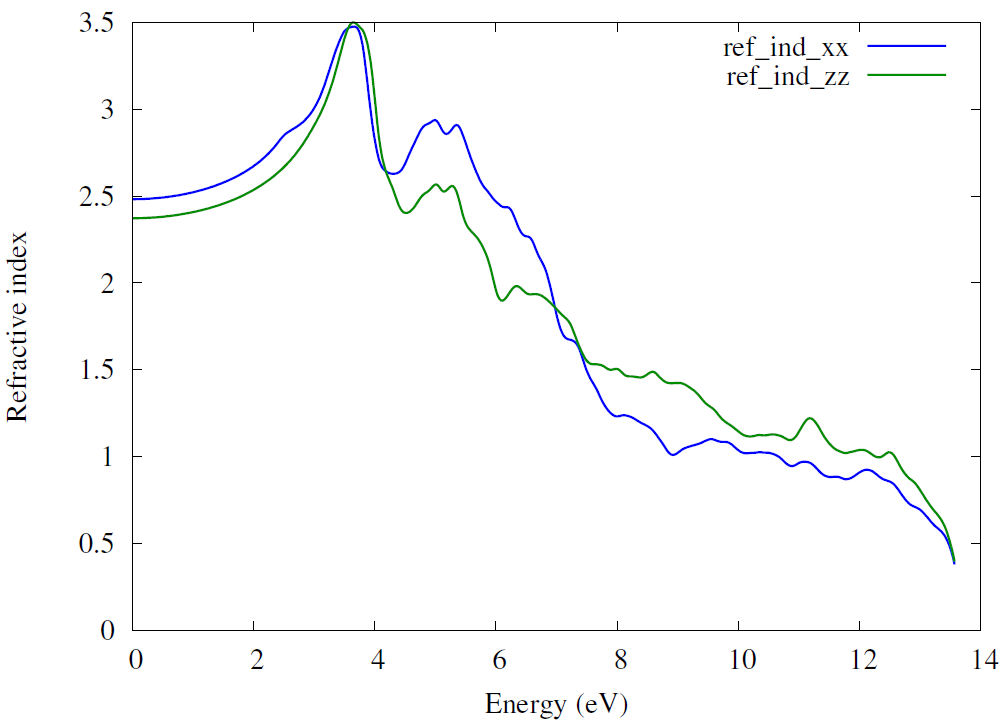
The plot of the refractive index of Zn₂NbN₃ is shown in Fig. 8, the value of static refractive index n(0) is 2.4 and 2.5 in zz direction and xx direction, respectively, indicating the semiconducting behavior of the compound. The main peak has a maximum value at 3.5 eV energy value, so Zn₂NbN₃ has a high refractive index, proving that our compound can be used in photonic applications. After 12 eV, the refractive index decreases when the energy of the incident photon increases and the value of n(ω) becomes less than one, providing the photoluminescence phenomenon, which means that the phase velocity of passing light through the material is greater than the light speed in a vacuum ^[33]. We can also observe a clear match between the plot of real part of dielectric function ε1(ω) and the plot of refractive index n(ω) Figs. 5 and 8 . The first peak in both plots is related to photons with minimal energy. After this peak, we notice a continuous decrease in both coefficients because of fluctuations.

Figure 8 Refractive index plot of Zn₂NbN₃.

3.3.4 Extinction coefficient

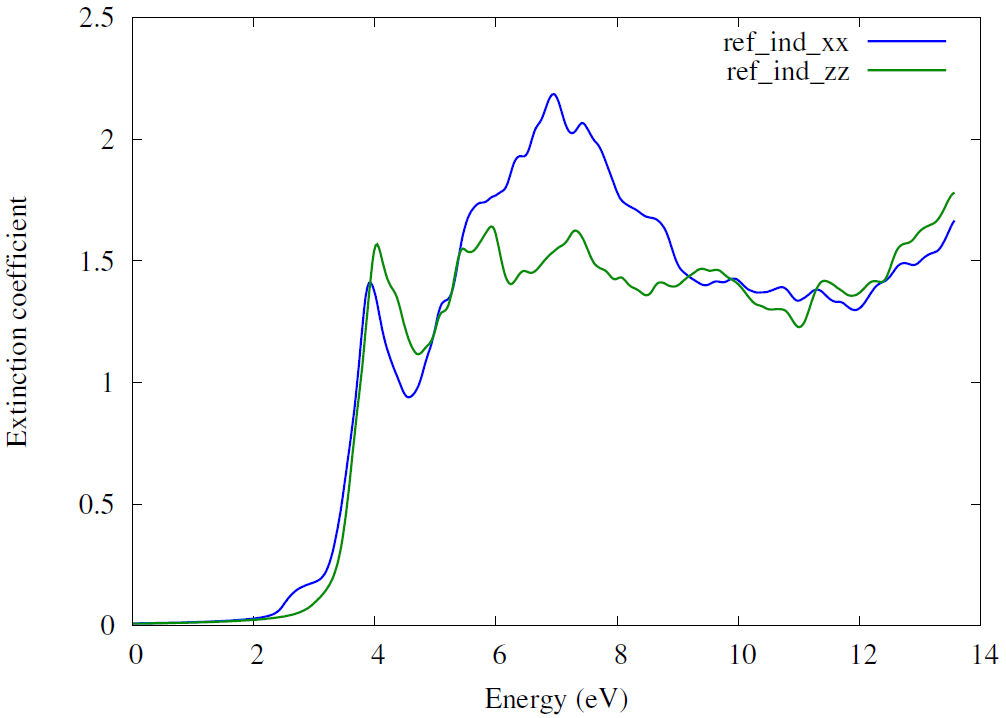
The extinction coefficient shows the amount of radiation absorbed by the material, which explains the similarity between the extinction coefficient and absorption coefficient plots. Extinction coefficient K(ω) can be also calculated using the values of ε1(ω) and ε2(ω) according to following relation ^[32].

K(ω)=ε12(ω)+ε22(ω)2-ε1(ω)2. (7)

Figure 9 shows extinction coefficient spectra. We can see the extinction coefficient close to zero in the energy range from 0.0 to 2.0 eV, which means that the electromagnetic wave can completely pass through the material. The first peak is of the order of 1.5, around 4.0 eV. An important peak of 2.2 occurs at 7.0 eV. Hence, the electromagnetic wave passes difficulty through the material after the energy of 2.0 eV.

Figure 9 Extinction coefficient K(ω).

4 Conclusion

We have computed structural, electronic, and optical properties for Zn₂NbN₃ by applying DFT theory-based FP-LAPW approach. Structural parameters are a = 9.90 Å and b = 5.81 Å and c = 5.43 Å. The electronic calculations obtained from band structure using both (GGA) and (TB-mBJ) approximations prove direct bandgap and semiconductor behavior. From total and partial DOS performed by employing (GGA) and TB-mBJ approximations, we have concluded that the main contribution is from Nb-d and N-p orbitals, in good agreement with the imaginary part of the dielectric function. The absorption of Zn₂NbN₃ appears after 3.1 eV, consistent with results from electronic properties, using (PBE) and (TB-mBJ) approximations. The Zn₂NbN₃ material has a high refractive index and strong optical absorption in the ultraviolet region. So, this compound is suitable for optoelectronic applications.

References

[1] F. Ponce, D. Bour, Nitride-based semiconductors for blue and green light-emitting devices, nature 386 (1997) 351-359. [ Links ]

[2] S. R. Bauers et al., Ternary nitride semiconductors in the rocksalt crystal structure, Proceedings of the National Academy of Sciences 116 (2019) 14829-14834. [ Links ]

[3] U. K. Mishra, P. Parikh, Y.-F. Wu, Algan/gan hemts-an overview of device operation and applications, Proceedings of the IEEE 90 (2002) 1022-1031. [ Links ]

[4] S. Nakamura, The roles of structural imperfections in ingan-based blue light-emitting diodes and laser diodes, Science 281 (1998) 956-961. [ Links ]

[5] R. Trew, M. Shin, V. Gatto, High power applications for gan-based devices, Solid-State Electronics 41 (1997) 1561-1567. [ Links ]

[6] K. Balasubramanian, S. V. Khare, and D. Gall, Valence electron concentration as an indicator for mechanical properties in rocksalt structure nitrides, carbides and carbonitrides, Acta Materialia 152 (2018) 175-185. [ Links ]

[7] X.-J. Chen et al., Hard superconducting nitrides, Proceedings of the National Academy of Sciences 102 (2005) 3198-3201. [ Links ]

[8] I. S. Khan, K. N. Heinselman, A. Zakutayev, Review of znsnn2 semiconductor material, Journal of Physics: Energy 2 (2020) 032007. [ Links ]

[9] M. Wittmer, Properties and microelectronic applications of thin films of refractory metal nitrides, Journal of Vacuum Science & Technology A: Vacuum, Surfaces, and Films 3 (1985) 1797-1803. [ Links ]

[10] Y. Hinuma et al., Discovery of earth-abundant nitride semiconductors by computational screening and highpressure synthesis, Nature communications 7 (2016) 1-10. [ Links ]

[11] A. Yoshikawa, E. Ohshima, T. Fukuda, H. Tsuji, and K. Oshima, Crystal growth of gan by ammonothermal method, Journal of crystal growth 260 (2004) 67-72. [ Links ]

[12] G. Kortüm, W. Braun, and G. Herzog, Principles and techniques of diffuse-reflectance spectroscopy, Angewandte Chemie International Edition in English 2 (1963) 333-341. [ Links ]

[13] M. Mallmann, C. Maak, R. Niklaus, and W. Schnick, Ammonothermal synthesis, optical properties, and dft calculations of mg2pn3 and zn2pn3, Chemistry-A European Journal 24 (2018) 13963-13970. [ Links ]

[14] A. Zakutayev, Synthesis of zn2nbn3 ternary nitride semiconductor with wurtzite-derived crystal structure, Journal of Physics: Condensed Matter 33 (2021) 354003. [ Links ]

[15] A. Zakutayev, S. R. Bauers, and S. Lany, Experimental synthesis of theoretically predicted multivalent ternary nitride materials, Chemistry of Materials 34 (2022) 1418-1438. [ Links ]

[16] M. Debbarma, S. Das, B. Debnath, D. Ghosh, S. Chanda, R. Bhattacharjee, S. Chattopadhyaya, Density functional study of elastic and thermal properties of cubic mercury-zinc-chalcogenide ternary alloys, Bulletin of Materials Science 43 (2020) 1-17. [ Links ]

[17] P. Blaha, K. Schwarz, G. K. Madsen, D. Kvasnicka, and J. Luitz, Computer code wien2k, Vienna University of Technology (2001). [ Links ]

[18] P. Blaha et al., wien2k, An augmented plane wave+ local orbitals program for calculating crystal properties 60 (2001). [ Links ]

[19] P. Blaha, K. Schwarz, F. Tran, R. Laskowski, G. K. Madsen, L. D. Marks, Wien2k: An apw+ lo program for calculating the properties of solids, The Journal of Chemical Physics 152 (2020) 074101. [ Links ]

[20] O. Farkad, F. Elfatouaki, S. Hassine, Y. Ijdiyaou, E. Ibnouelghazi, D. Abouelaoualim, Structural, electronic and optical properties of ab bilayer graphene intercalated by sr atom: A first principles study, Diamond and Related Materials 126 (2022) 109082. [ Links ]

[21] J. Toulouse, Review of approximations for the exchange-correlation energy in density-functional theory, arXiv preprint arXiv:2103.02645 (2021). [ Links ]

[22] H. Xiao, J. Tahir-Kheli, W. A. Goddard III, Accurate band gaps for semiconductors from density functional theory, The Journal of Physical Chemistry Letters 2 (2011) 212-217. [ Links ]

[23] J. P. Perdew, K. Burke, and M. Ernzerhof, Generalized gradient approximation made simple, Physical review letters 77 (1996) 3865. [ Links ]

[24] F. Elfatouaki et al., A dft study of the structural, electronic and optical properties of csgei 2 br halide perovskite, in: 2020 5th International Conference on Renewable Energies for Developing Countries (REDEC), IEEE, 2020, pp. 1-4. [ Links ]

[25] R. Takassa, O. Farkad, E. Ibnouelghazi, and D. Abouelaoualim, Structural and electronic properties of ndoping ultra-small diameter (3,3) armchair swcnt by using pbe and tb-mbj potentials, Applied Surface Science 563 (2021) 150283. [ Links ]

[26] I. Khare, N. Szymanski, D. Gall, R. Irving, Electronic, optical, and thermoelectric properties of sodium pnictogen chalcogenides: A first principles study, Computational Materials Science 183 (2020) 109818. [ Links ]

[27] N. Szymanski, V. Adhikari, M. Willard, P. Sarin, D. Gall, and S. Khare, Prediction of improved magnetization and stability in fe16n2 through alloying, Journal of Applied Physics 126 (2019) 093903. [ Links ]

[28] G. Rehman et al., Electronic band structures of the highly desirable iii-v semiconductors: Tb-mbj dft studies, Journal of Electronic Materials 45 (2016) 3314-3323. [ Links ]

[29] C. Sifi et al., First principle calculations of structural, electronic, thermodynamic and optical properties of pb1- xcaxs, pb1- xcaxse and pb1- xcaxte ternary alloys, Journal of Physics: Condensed Matter 21 (2009) 195401. [ Links ]

[30] F. Drief, A. Tadjer, D. Mesri, H. Aourag, First principles study of structural, electronic, elastic and optical properties of mgs, mgse and mgte, Catalysis Today 89 (2004) 343-355. [ Links ]

[31] I. Moreels, G. Allan, B. De Geyter, L. Wirtz, C. Delerue, and Z. Hens, Dielectric function of colloidal lead chalcogenide quantum dots obtained by a kramers-krönig analysis of the absorbance spectrum, Physical Review B 81 (2010) 235319. [ Links ]

[32] S. Azam et al., Dft study of the electronic and optical properties of ternary chalcogenides alx2te4, Materials Research Express 6 (2019) 116314. [ Links ]

[33] M. Sotudeh, A. Boochani, S. S. Parhizgar, S. R. Masharian, Optical and electronic properties of zigzag boron nitride nanotube (6, 0): Dft study, International Nano Letters 10 (2020) 293-301. [ Links ]

[34] B. Rameshe, M. Rajagopalan, B. Palanivel, Electronic structure, structural phase stability, optical and thermoelectric properties of sr2alm’o6 (m’= nb and ta) from first principle calculations, Computational Condensed Matter 4 (2015) 13-22. [ Links ]

[35] M. Caid, H. Rached, A. Bentouaf, D. Rached, and Y. Rached, High-throughput study of the structural, electronic, and optical properties of short-period (bese) m/(znse) n superlattices based on dft calculations, Computational Condensed Matter 29 (2021) e00598. [ Links ]

Received: March 15, 2022; Accepted: August 21, 2022

^* e-mail: dr.abouelaoualim@uca.ac.ma

This is an open-access article distributed under the terms of the Creative Commons Attribution License