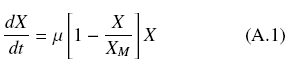
Appendix

Appendix A

Mathematical model of mold growth on solid surfaces

It is assumed that a mycelial fungus grows over a solid surface with area, A, producing quantity, X (grams in dry basis) according to the logistic equation, as follows

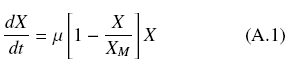
Where, μ (h^-1), is the initial rate of growth when, 0 < X « X_M, and X_M is the maximal biomass quantity to be produced on that solid surface. The limiting substrate, i.e. the carbon source, is distributed evenly within the solid support with volume, V, at initial concentration, S₀. Hence the initial amount of substrate is Q₀ = S₀V. The rate of substrate uptake is given by the following expression.

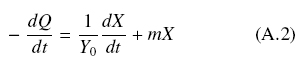
where, Y₀, is the maximal yield (g of X per g of S ) and m (g S/gX*h), is the maintenance coefficient.

Combining Eqs. (A.1) and (A.2) and after integration, the following expression is obtained

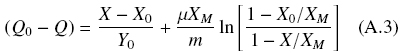
After some rearrangement, assuming that, X₀ « X < X_M, and defining, Φ = X/X_M, it is possible to estimate the decrease of the substrate, -ΔQ = Q₀ - Q, as follows

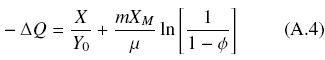
After a very long period of time, Φ → 1, X → X_M, and Q → 0

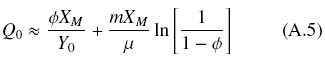
Assuming, Φ = 0.99996, an approximate estimate of 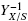= Q₀/X_M , is obtained

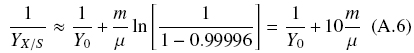
Equation (A6) shows that the inverse of the apparent yield, 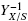, increases with the ratio, m/μ, which is an indication of how much substrate was used to make other products different from biomass. When the ratio, m/μ is very small, the yield is maximal ( 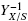→ Y₀)

The experimental evidence shows that the inverse yield is proportional to σ₀, according to Eq. (A7) that can be compared to Eq. (A6)

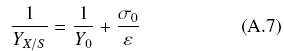
Therefore, 1/ε, is an index of the efficiency of biomass production because it is proportional to the ratio, m/μ. Furthermore, if the volumetric biomass density,_ρV, is almost constant, the total amount of biomass over the surface is given by

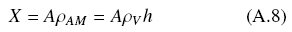
Where, h, is the average thickness of the fungal layer distributed with final average surface density, _ρAM. Again, experimental evidence shows that Eq. (4) holds, and for the sake of clarity is repeated as

When σ₀ » K, the thickness reaches its maximal value h ≈ h_max, and from Eq. (3) and assuming complete substrate utilization (ƒ ≈1), .Eq. (A.10) is obtained

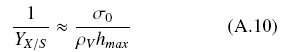
From Eq. (A.7) for large values of σ₀, Eq. (A.11) is obtained

Hence, comparing eqs. (A10) and (A11), the following identification is obtained, ε = _ρVh_MAX. Therefore, the parameter ε is the maximal amount of biomass per unit area. For example, a mutant strain that is diverting most of the substrate to collateral products will be less productive than a wild type that has evolved to be highly productive with little diversion of the substrate in collateral products. Also, a column of packed bed particles could have more hindrance for the growth of the fungal layer than an open surface of a Petri dish. This is analyzed in the Discussion.

Appendix B

Optimal size of supports for solid state fermentation

Fungal cultures growing on the surface of solid support will have optimal dimensions when the initial amount of the substrate, Q₀, is just enough to support a fungal layer that is fully oxygenated. In order to calculate the size of the solid support it is necessary to make an analysis of mass transfer of oxygen through the fungal mat. This should consider the fact that there are two inter-phases, a) A lower inter-phase with the solid support where the nutritive liquor is embedded and b) An upper inter-phase with air from which oxygen diffuses in a passive way following the Fick’s law as follows. The mass resulting mass balance is given in (B1) and is illustrated in Fig. 3.

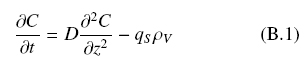
Where, z = 0, corresponds to the aerial inter-phase, and z = h, corresponds to the inter-phase with the solid substrate. The steady-state solution of Eq. (B1) yields the following equation

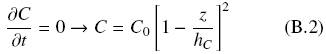
This equation is consistent with the boundary condition, C = C₀, for z = 0, and also with C ≈ 0, for z = h_C, as indicated by Hill (1929) and Pirt (1966, 1967). The value of h_C = 0.006 cm has been reported by Oostra et al. (2001) for Rhizopus oligosporus, and h_C = 0.0082 cm by Rahardjo et al. (2002) for Aspergillus oryzae. Thus, if h > h_C, oxygen will be practically absent (anaerobic layer) as suggested in Fig. 3.

If _ρV is the average volumetric density, the following mass balance holds

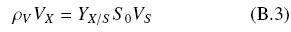
Where, V_X is the volume of the fungal layer and V_S is the volume of the solid support. An important restriction on fungal growth is to assume that the amount of initial substrate, Q₀ = S₀V_S, is just enough to support the growth of an aerobic fungal layer with uniform thickness h_C and Y_X/S = Y₀. Therefore, the optimal ratio, V_x/V_S, can be derived from Eq. (B3) yielding

Restrictions for aflat solid support of fungal cultures

Assuming that the solid support is a slab (agar plate), with area, A, and height H, (V_S = AH) and recalling that the final surface fungal density is _ρAM = _ρVh_C, the following relation holds

Defining, Λ = h_C/H and M = Y₀S₀/_ρV, the following equation is obtained

This simple equation indicates that the optimal height, H_opt, of the solid support is proportional to the product of the oxygen penetration depth, h_C, times the ratio between the average biomass density over the optimal yield as shown by

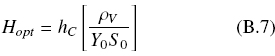
For example, for a fungal culture, with h_C = 0.01 cm, supplied with initial glucose concentration, S₀ = 0.01 gScm^-3, maximal yield, Y₀ = 0.5 gX/gS, and biomass density, _ρV = 0.05 gXcm^-3, the optimal height of the agar plate will be H_opt = 0.1 cm. For cultures with H > H_opt, the apparent yield will be lower than Y₀ because part of the biomass will be anaerobic. This calculation can have implications for the design of culture media with different values of biomass yields, but with the same initial substrate concentrations, by choosing different heights of the agar plate.

Restrictions for solid supports of fungal cultures with cylindrical and spherical geometries

The fungal layer can be considered as a shell with external radius, R + h_C, and with internal radius, R, length, L, and volume, V_X = (4π/3)[(R + hC)² - R²]L. Also, the solid support has a volume V_S = (4π/3)R²L. Hence, the mass balance Eq. (B3) leads to

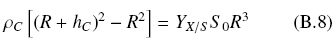
Solving for, Λ = h_C /R, as a function of M, the following equation is obtained.

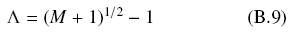
In a similar fashion, the mass balance of Eq. (B3) yields Eq. (B8) for solid support particles with spherical geometry.

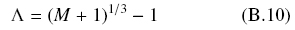
The corresponding optimal radius, R_opt, for cylindrical or spherical particles are given by eqs. (B.9) and (B.10), respectively

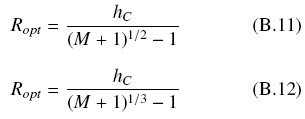
For example, for a fungal culture grown on the surface of small spherical particles, with h_C = 0.01 cm, supplied with initial glucose concentration, S₀ = 0.1 gScm^-3, maximal yield, Y₀ = 0.5 gX/gS, and biomass density, _ρV = 0.05 gXcm^-3, the optimal particle radius will be R_opt = 0.038 cm. This calculation indicates that fungal cultures with hypertonic syrups can have maximal biomass yield if they grow on small solid particles embedded with the hypertonic broth. It is worth noticing that reported values of oxygen penetration depths (h_C < 0.01 cm) and measured biomass density _ρV = 0.05 gcm^-3, give an approximate superficial density, _ρAM = 0.005 gcm^-2, which is lower than the parameter ε = 0.009 gcm^-2 discussed in Appendix A and calculated from data published by Favela-Torres et al. (1998).