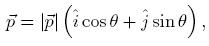
Como ilustracion, encontramos en este apéndice los autoestados de helicidad para el caso en el que el movimiento de la partícula se lleve cabo en el plano xy,
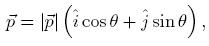
entonces
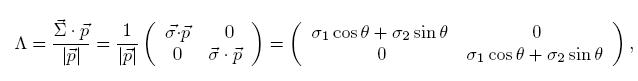
explícitamente
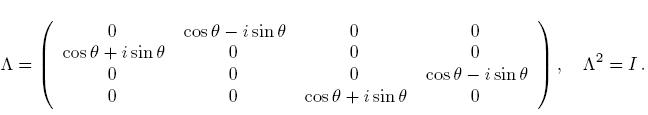
Su cuadrado es la matriz identidad y sus eigenvalores son λ ± 1.
Los eigenestados de helicidad se obtienen considerando la siguiente ecuación:
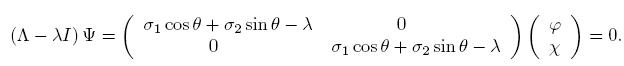
Es decir φ = χ, y para λ = ±1 se obtienen los estados de helicidad positiva y negativa ψ± =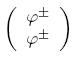
Resulta particularmente para el caso de movimiento en el plano (x,y)
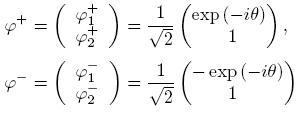
Formalmente, el espín está caracterizado por el operador de Pauli–Lubanski W α
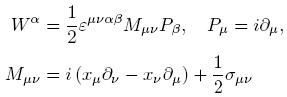
El invariante W αWα que conmuta con todos los generadores del grupo de Poincare, incluye al espín s para partículas masivas.
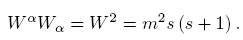
El estado cuíantico de una partícula masiva se describe en términos de la masa y el espín s y éste determina el comportamiento estadístico de la partícula. En este contexto, el operador helicidad se define como
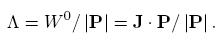
Para partículas sin masa, para las cuales Pµ Pµ = 0, el operador Λ conmuta con todos los generadores del grupo de Poincare y Λ → λ = ±s
Explícitamente
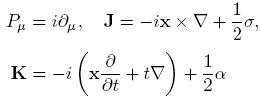
donde operador J es el momento angular y K es el operador de empuje (boost) [4].