7. ANEXOS

7.1. Questionário

1. Explique, por palavras suas, o que entende por função.

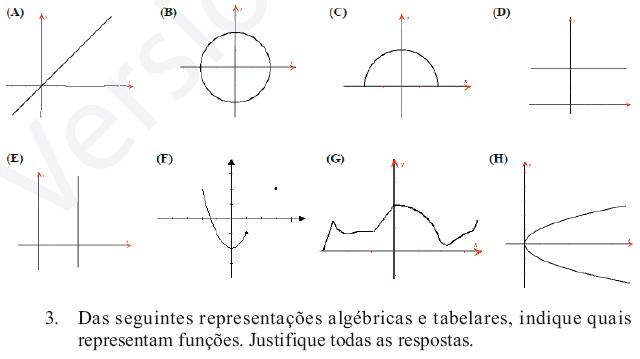
2. Das seguintes representações gráficas, indique quais representam funções e quais não representam funções. Justifique as que considera não se tratarem de uma função.

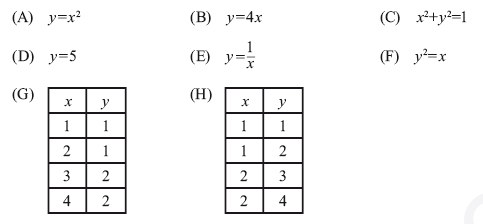
3. Das seguintes representações algébricas e tabelares, indique quais representam funções. Justifique todas as respostas.

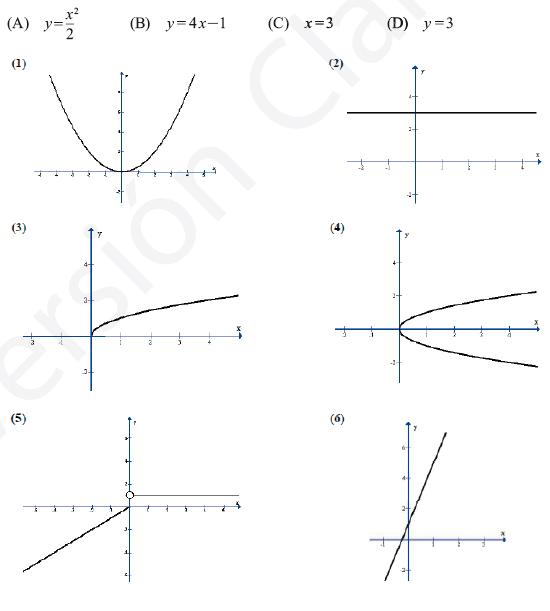
4. Em seguida, encontram-se algumas expressões algébricas e representações gráficas. Estabeleça,justificando, a correspondência entre as que considera que representam a mesma função.

7.2. Transformações de Funções

Partindo de representações gráficas de algumas funções é possível obter a representação gráfica de outras por transformações na expressão algébrica, como teve oportunidade de verificar anteriormente.

Considere a função real de variável real ƒ (x)=x³.

1. Utilizando a calculadora gráfica, visualize a representação gráfica da função e faça um esboço da mesma no papel.

2. Visualize as representações gráficas de funções definidas por expressões do tipo g(x)=ƒ (x)+a, atribuindo a a diferentes valores. Compare as representações gráficas obtidas.

3. Considere a família de funções obtidas a partir da função ƒ através da expressão h (x)=ƒ (x+b), observando a influência do parâmetro b. Visualize as representações gráficas de funções desta família e compare as representações obtidas.

4. Visualize as representações gráficas de funções definidas por expressões do tipo i(x) = cƒ (x), atribuindo a c:

- valores superiores a 1;

- valores positivos, mas inferiores a 1;

- valores iguais ou inferiores a -1;

- valores negativos, mas superiores a -1.

Para cada um destes casos, compare as representações gráficas obtidas e registe as suas conclusões.

7.3. FunçõesPoíinomiais

Considere as funções:

- f (x)=x+3, uma função polinomial de grau um;

- g, uma função polinomial de grau dois, definida por uma expressão da forma.

g(x) = ax²+bx+c (a,b,c ∈ R e a≠0

- h, que resulta do produto dos polinómios que definem as funções ƒ e g.

1. As funções ƒ e g admitem as seguintes representações gráficas, para certos valores de a, b e c:

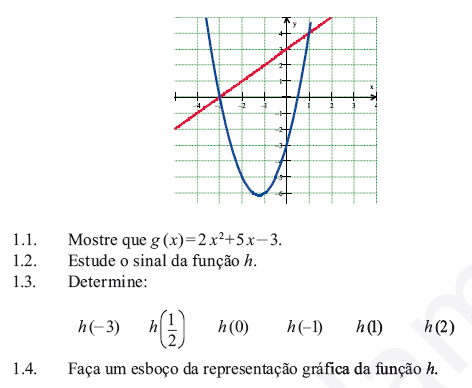
2. Procure novos valores para os parâmetros a, b e c, de modo que:

2.1. a função h tenha apenas um zero real;

2.2. a função h tenha mais do que dois zeros reais e distintos.

Quais as alterações que se podem observar nas representações da função h?