Apéndice

Derivación de la fórmula (32)

Del problema de optimización planteado en (29), las condiciones de primer orden son:

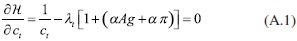
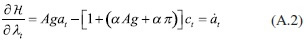
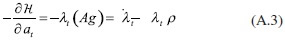
Después de despejar el consumo de (A.1), se obtiene:

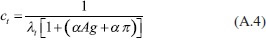
Al factorizar de (A.3) λ_t, y, posteriormente, despejar λ_t, se sigue que

Si x, = αx_t la solución de la ecuación diferencial es de la forma x_t = x₀^αt, entonces las soluciones de las ecuaciones diferenciales (A.2) y (A.5) son respectivamente:

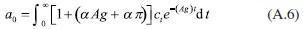
Si se sustituye (A.7) en (A.2), se obtiene:

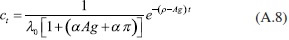
Al sustituir la ecuación (A.8) en (A.6), se tiene:

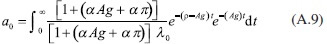
Después de simplificar se produce la siguiente ecuación:

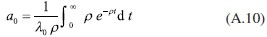
Observe que 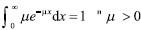entonces

De esta manera, cuando se sustituye la ecuación (A.11) en (A.8), se encuentra la trayectoria del consumo:

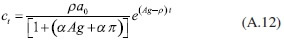
Derivación de la ecuación (33)

Si se sustituye la ecuación (A.12) en (A.2), se obtiene:

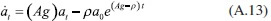
Se sabe que si x^._t = αx_t+f(t) 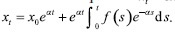, entonces la solución es de la forma ds. Por tanto, se obtiene que:

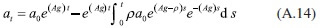
Al resolver, la ecuación anterior, se sigue que:

Derivación de las ecuaciones (42) y (43)

Las condiciones de primer orden del problema planteado en (39) son:

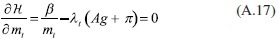
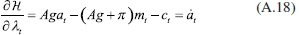
Por tanto, al despejar el consumo de (A.16) y los saldos reales de (A.17), se tiene respectivamente que:

y

Después de despejar λ, de (A.19), resulta:

Una vez determinadas las ecuaciones diferenciales (A.18) y (A.22), si se supone que 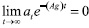se tienen, respectivamente,

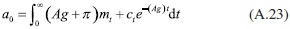
y

Si se sustituye la ecuación (A.24) tanto en (A.20) como en (A.21), se obtienen:

y

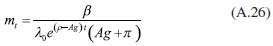
Si se sustituyen ahora las ecuaciones (A.25) y (A.26) en la ecuación (A.23), resulta que:

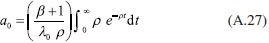
En consecuencia, debido a que 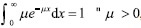si se despejan 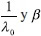se llega a que:

y

Por último, para encontrar la trayectoria del consumo se sustituye la ecuación (A.28) en (A.25), y para hallar la trayectoria de los saldos reales se sustituye la ecuación (A.29) en (A.26), con lo que se obtienen, respectivamente:

y