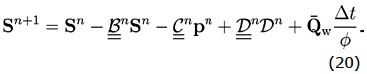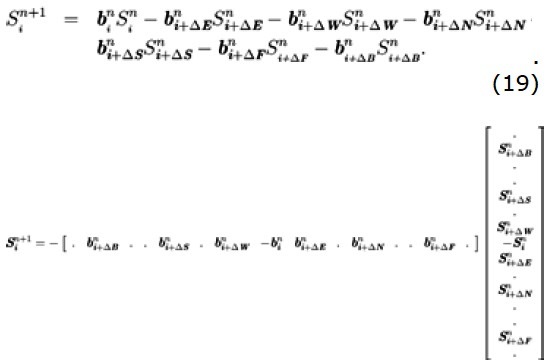
Appendix C

The main idea is to restate the discretized saturation equation (11) in a more convenient, linear algebra representation, to exploit the features of the parallel libraries evaluated. Every element of the N-size mesh can be mapped to an element of a vector of size N. Any arbitrary volume P, with neighbors set NB∈;{E, W, N, S, F, B} must be identified by an index i, with 1<i<N, and the corresponding neighbor set NB_i comes {i+ΔE, i+ΔW, i+ΔN, i+ΔS, i+ΔF, i+ΔB}, where ΔI keeps the distance of the neighbor from the element inside the vector containing them, with I∈{E, W, N, S, F, B}.

Next, applying this notation to every term in equation (11), and showing only terms involving b for simplicity, we get

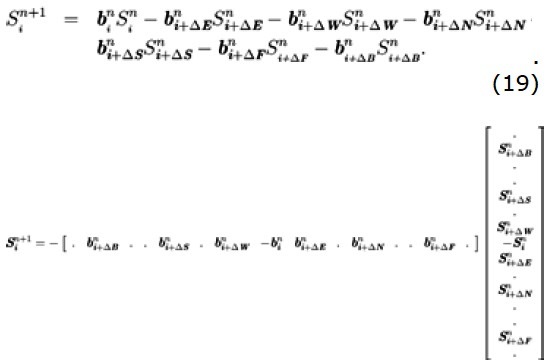
The row vector of the last relation is, indeed, a row of a matrix N × N, in which every row has a corresponding relation of some element of the -size mesh. The N-size column vector contains the saturation in the elements of the mesh at time n. Defining matrices and for the terms related to cⁿ and dⁿ respectively in the equation (11), we get a final linear algebra version of the saturation equation