Anexo metodológico

A.1. Curva de Lorenz

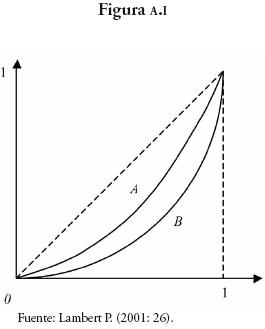
Es uno de los instrumentos de análisis de la desigualdad de la renta más básicos que existen, pero también es uno de los más ilustrativos y prácticos, especialmente cuando se trata de comparar diferentes distribuciones de la renta f(y), ya que estandariza el nivel de renta para su medición.

La idea básica es ordenar las unidades de ingreso por su nivel de magnitud, empezando por el nivel más bajo y graficando contra la proporción acumulativa de la población que le corresponde, en ambos casos, tanto el ingreso como la población han de normalizarse, de forma que tomen valores que van de 0 a 1. Así, si existiese un distribución del ingreso muy desigual, los cuantiles (porciones) poblacionales con mayor ingreso recibirán una renta más que proporcional al tamaño de su población, mientras que los cuantiles menores recibirán una renta menos que proporcional. De esta manera, ante el hipotético caso de una total igualdad en la distribución del ingreso, cada cuantil poblacional recibirá exactamente el mismo cuantil de renta que le corresponde, donde cada individuo tendría el ingreso promedio (µ) y la curva de Lorenz sería una línea de 45°.

Es fácil comparar en la figura A.I dos distribuciones de ingreso familiar, la curva A es menos desigual que la B, ya que está más cerca de la línea de igualdad.

En el caso de que la curva de Lorenz para una función continua sea L(p), 0≤ p≤ 1, el ingreso del primer 100p por ciento de unidades de ingreso es 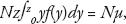de manera que la curva de Lorenz L(p) en el p–valor se define como:

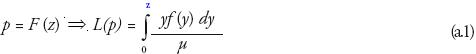
A.2. Curva de concentración

Cuando se grafican porciones de una variable x contra quintiles en la distribución de otra y, se llama curva de concentración y se compara con la curva de Lorenz, por lo que puede situarse por arriba o debajo de ésta, de modo que la diferencia entre ambas captura las diferencias en la clasificación de las distribuciones. Éstas son muy usadas en el análisis de los efectos distributivos de los impuestos y transferencias públicas. Debe decirse que en las curvas de concentración no se ordenan los valores de la variable en cuestión de menor a mayor, sino simplemente se mantiene el orden preestablecido de la variable de referencia, la cual en la mayoría de las veces es el ingreso.

A.3. Coeficiente de concentración

Se le llama al área que se encuentra entre la curva de concentración y la línea de 45°, de manera análoga a como lo hace el coeficiente de Gini. Sus valores se encuentran entre –1 para concentraciones sobre los ingresos más bajos de la variable en cuestión, y +1 cuando la concentración se acentúa en los estratos con más ingresos, mientras que 0 indica una distribución neutral, lo que implica que cada persona o decil presenta una misma participación en la variable. Así, para el caso donde se analizan los efectos que tiene una transferencia determinada sobre el ingreso, el coeficiente de concentración para el ingreso postransferencia es:

Analizando el efecto que una transferencia tiene sobre el ingreso, se define a la curva de Lorenz pretransferencia L_B(p) como:

Lo cual muestra que la curva de Lorenz L_Y del ingreso pretransferencia es un promedio ponderado de las curvas de concentración de transferencias L_B y del ingreso postransferencia L_Y–B. Por tanto,

Esta desigualdad indica que para que el ingreso postransferencia sea más equitativo que el ingreso pretransferencia, la transferencia sobre el ingreso deberá ser más equitativo que el ingreso pretransferencia

A.4. Índice de Kakwani y progresividad

La pregunta que surge ahora es cómo capturar esa nueva desproporcionalidad creada por una transferencia progresiva y su efecto redistributivo en el ingreso. En este sentido, un índice de progresividad tiene la ventaja de capturar en un número la estructura de transferencias b(y) y la distribución de la renta pre f(y) y post f’(y) transferencias.

La desproporcionalidad de un impuesto o transferencia progresiva se aprecia en la distancia existente entre las curvas L_Y y L_B, de manera que a mayor separación entre ellas mayor será el efecto de desproporcionalidad. Esta idea se complementa con lo señalado por Musgrave y Tun (1948), para quienes entre más desigual sea la distribución del ingreso antes de una transferencia progresiva, más fuerte será su efecto ecualizador.

De esta manera surge el índice de Kakwani, el cual mide la progresividad en términos de la separación de las curvas L_Y y L_B, a través de un índice que calcula dos veces el área existente entre ambas curvas.

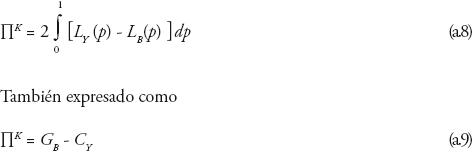
Así, Π^K aumentará si la progresividad de una transferencia se incrementa para cada nivel de ingreso, mientras la distribución del ingreso pretransferencia permanezca constante, aumentando así la progresividad efectiva.

Debe decirse que los límites de este índice dependerán de la desigualdad de la distribución pretransferencia, y es (–1+G_y ) el límite inferior y (1+G_y ) el límite superior.