ANEXO

ACTIVIDADES PRESENTES EN EL PROGRAMA DE MATEMÁTICA PARA PRIMER AÑO DE LAS ESCUELAS MEDIAS DE LA CIUDAD AUTÓNOMA DE BUENOS AIRES, SECRETARÍA DE EDUCACIÓN DEL GOBIERNO DE LA CIUDAD DE BUENOS AIRES

Actividad 1

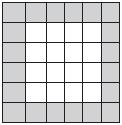
El objetivo final de esta actividad es encontrar una fórmula que permita calcular el número de cuadritos sombreados de una figura como la del modelo, cualquiera que sea el número de cuadritos sobre el lado del cuadrado.

Una posible gestión es la siguiente:

• dar primero un cuadrado dibujado con 5 o 6 cuadritos de lado y pedir su conteo;

• preguntar después cuántos cuadritos habrá en el borde de un cuadrado de 37 cuadritos de lado;

• reunidos en grupos, los alumnos deben confrontar las soluciones y elegir una para hacerla pública;

• se solicita a cada grupo la explicación del método utilizado para contar en el caso 37, de manera que pueda servir para contar en otros casos;

• discusión de los métodos de cálculo (que se supone que estarán dados en lenguaje usual);

• se propone luego a los alumnos que escriban una fórmula que refleje el método que elijan (el propio o alguno de otro grupo que prefieran);

• discusión de las diferentes fórmulas obtenidas (se espera una pluralidad de fórmulas correctas);

• se trabaja sobre la noción de equivalencias de fórmulas;

• se plantean a los alumnos diferentes preguntas que muestren la utilidad de la fórmula para conocer características de la situación que modeliza.

Se trata de un ejemplo en el que la diversidad de maneras de contar los cuadritos sombreados dará origen a diferentes escrituras para la fórmula buscada, permitiendo la discusión en torno a la equivalencia de ellas. En este problema se pone en juego el uso de la propiedad distributiva para expresiones algebraicas.

Una cuestión esencial del trabajo algebraico es la lectura de información en una expresión. En este caso, frente a preguntas del tipo: ¿existe algún valor de n para el cual la cantidad de cuadraditos sombreados sea 587?, los alumnos deberán reconocer en la lectura de la expresión 4n — 4, que eso no es posible, ya que 587 no es múltiplo de 4. ¿Por qué hacemos referencia a la lectura de información en una expresión en el planteo de esta pregunta? Obsérvese que si los alumnos conocen que todo múltiplo de 4 puede expresarse como el producto de 4 por cualquier número entero, al expresar 4n — 4 como 4 (n - 1) podrán percibir que al reemplazar por cualquier valor natural, siempre se obtendrá como resultado un múltiplo de 4 y, por lo tanto, no existirá ningún n para esta fórmula de 587.

Actividad 2

Se propone la siguiente sucesión de figuras, construidas con fósforos y se aclara cómo se continúan armando.

Esquema de tareas para los alumnos:

a)  Se les pide calcular la cantidad necesaria de fósforos para construir la figura que ocuparía el sexto lugar.

b)  Se pregunta por la cantidad de fósforos necesarios para construir la figura del lugar 100 en la sucesión.

c)  Se solicita una fórmula para la cantidad de fósforos de la figura del lugar n y se trabaja la equivalencia de distintas fórmulas si es que aparecen (son probables 3n + 1 y 4 + 3(n - 1)).

d)  Se formulan preguntas para hacer funcionar la fórmula. Por ejemplo: ¿podrá ser que en alguna ubicación la figura tuviera 1 549 fósforos? Si tengo 1 500 fósforos y armo una figura de esta forma lo más grande posible, ¿me sobra alguno?

SITUACIÓN PLANTEADA POR GUSTAVO BARALLOBRES EN SU INVESTIGACIÓN

Parte 1

El profesor dará diez números consecutivos y el equipo que primero encuentre la suma de estos números será el ganador. No es posible usar calculadora.

El docente propone, a continuación, comenzar a jugar con la siguiente lista de números:

1a. partida: 19, 20, 21, 22, 23, 24, 25, 26, 27, 28.

Luego de finalizada esta partida se propone la segunda:

2a. partida: 783, 784, 785, 786, 787, 788, 789, 790, 791, 792.

El docente puede jugar más partidas, si lo cree necesario, con la idea de ir generando en los alumnos la necesidad de buscar métodos económicos. Posteriormente, el docente explica a los alumnos que ahora les dará un tiempo, antes de darles otros diez números consecutivos, para que puedan pensar alguna estrategia que les permita ganar rápidamente.

Cuando todos los grupos manifiesten haber diseñado alguna estrategia, el docente propondrá nuevas partidas:

3a. partida: 6985, 6986, 6987, 6988, 6989, 6990, 6991, 6992, 6993, 6994. (Si es necesario, pueden proponerse más partidas.)

Comentario: Las primeras partidas se juegan sin condicionamientos. El primero que obtiene el resultado lo propone y el docente propone al resto de la clase controlar si es correcto o no. En caso de obtenerse una respuesta incorrecta, el juego continúa hasta que aparezca la primera respuesta correcta.

Como habrá grupos que responderán más rápidamente que otros, se trata de que aquellos que realicen todas las cuentas se vean "forzados" a buscar otros procedimientos. Por esta razón, el docente analizará cuántas partidas se juegan hasta generar esta necesidad de búsqueda para luego proponer la tercera partida. En esta instancia, no hay ningún tipo de discusión sobre la manera de obtener los resultados; cada equipo tendrá que no divulgar la estrategia que supuestamente le permite ganar el juego.

Parte 2

En esta instancia, el docente anuncia a los alumnos que existen fórmulas que permiten, dado el primero de los diez números consecutivos cualesquiera, obtener como resultado la suma de esos diez números, y que ahora se trata de encontrar una de estas fórmulas.

Parte 3

Cada grupo tendrá que buscar razones para que el resto de la clase pueda comprender por qué la fórmula encontrada sirve para cualquier secuencia de diez números consecutivos.

Tendrán un tiempo para trabajar en el grupo y acordar las razones que expondrán posteriormente.

El docente será el encargado de conducir el debate, cuya finalidad es que cada grupo pueda exponer sus razones y que éstas sean discutidas y aceptadas o rechazada por el resto de la clase.

Posteriormente, el docente recupera todas las explicaciones proporcionadas por los diferentes grupos y las presenta al conjunto de la clase (puede ser en hojas fotocopiadas). Cada grupo deberá analizar las diferentes producciones y decidir cuál es la que elegirá para que todos puedan comprender por qué cada fórmula encontrada sirve para cualquier secuencia de diez números consecutivos. Se deberán proporcionar razones por las cuales elige una de estas explicaciones y razones por las cuales descarta las otras.