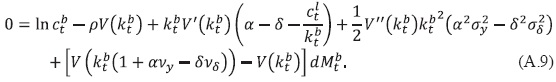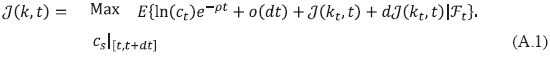
Apéndice matemático

Derivación de la ecuación (9)

El problema de control óptimo planteado por (2) y (8') arroja que:

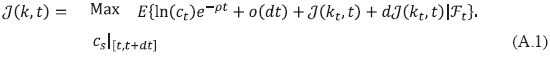
Por su parte, el Lema de íto establece que:

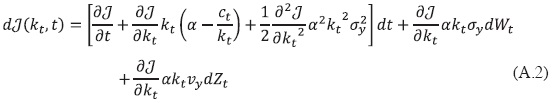
Para encontrar la ecuación (9) se necesita sustituir 𝒥(k_t, t) = V(k_t)e^-ρt y aplicar (A.2) a la ecuación (A.1), posteriormente tomar esperanzas y fijar E(dz) = 0, dividir entre dt y tomar el límite cuando t → 0 , con lo que se obtiene lo siguiente:

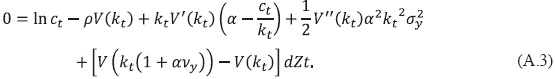
Derivación de la ecuación (34)

El problema de control óptimo planteado por (2) y (32'), arroja que:

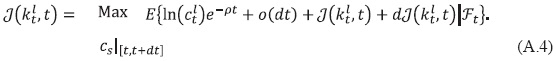
Por su parte, el Lema de íto establece que:

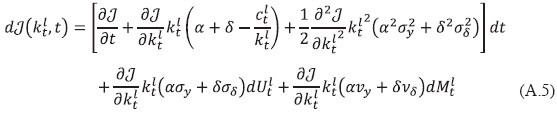
Para encontrar la ecuación (34) se necesita sustituir 𝒥(k^l_t, t) = V(k^l_t)e^-ρt y aplicar (A.5) a la ecuación (A.4), posteriormente tomar esperanzas y fijar E(dM_t) = 0, dividir entre dt y tomar el límite cuando t → 0, con lo que se obtiene lo siguiente:

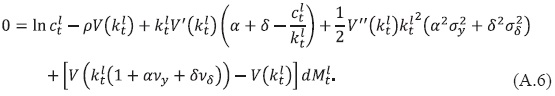
Derivación de la ecuación (54)

El problema de control óptimo planteado por (2) y (33'), arroja que:

Por su parte, el Lema de Îto establece que:

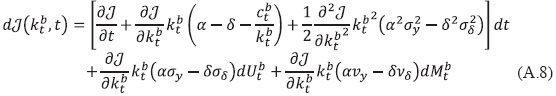
Para encontrar la ecuación (54) se necesita sustituir  𝒥(k^b_t, t) = V(k^b_t)e^-ρt y aplicar (A.8) a la ecuación (A.7), posteriormente tomar esperanzas y fijar E(dM_t) = 0 , dividir entre dt y tomar el límite cuando t → 0, con lo que se obtiene lo siguiente: