
ALM practices, multiple uncertainties and monopolistic behavior: a microeconomic study of banking decisions1
Antonio Ruiz-Porras2
2 Email: antoniop@cucea.udg.mx. Address for correspondence: Departamento de Métodos Cuantitativos. Universidad de Guadalajara, CUCEA. Periférico Norte 799, Núcleo Universitario Los Belenes, 45100, Zapopan, Jalisco, México. Tel: + (52) (33) 3770 3300, Ext. 25291. Fax.: + (52) (33) 3770 3300, Ext. 25227.
Recepción: 11/04/2011 ]]> Aceptación: 16/08/2011
Abstract
We study the decisions that a monopolistic bank takes to achieve risk management and profit objectives. The bank faces liquidity and solvency risks because loans may not be repaid and because unexpected deposit withdrawals may occur. The Asset-Liability-Management (ALM) banking model shows that compromise solutions are necessary to deal with the tradeoffs between liquidity management and profitability. It also shows that asset management practices increase profits. Moreover it shows that liability management practices and market power support profitability. Finally, the model confirms that banks should undertake long-term risky investments when depositors trust the viability of the asset transformation process.
Keywords: Banking, ALM, multiple uncertainties, monopolistic behavior.
Classification JEL: G21, G32, D81, L21.
Resumen
Estudiamos las decisiones tomadas por un banco monopólico para alcanzar objetivos de administración de riesgos y de rentabilidad. El banco enfrenta riesgos de liquidez y solvencia porque los préstamos pueden no ser pagados y porque pueden ocurrir inesperados retiros de depósitos. El modelo bancario de administración de activos y pasivos (ALM) muestra que las soluciones de compromiso son necesarias para manejar los dilemas entre la administración de la liquidez y la rentabilidad. También muestra que las prácticas de administración de activos pueden incrementar las ganancias. Más aún, muestra que las prácticas de administración de pasivos y el poder de mercado sustentan la rentabilidad. Finalmente, el modelo confirma que los bancos deben asumir inversiones riesgosas de largo plazo cuando los depositantes confían en la viabilidad del proceso de transformación de activos.
]]> Introduction
Banks perform essential activities to guarantee an efficient allocation of resources within the economy. Banking activities aim to provide access to liquidity and payment services, to transform assets, to manage risks and to monitor and process information [Freixas and Rochet (2008)]. Such activities involve uncertainties and the management of different types of risks. The management of risks regarding assets, liabilities and liquidity characterizes banking institutions. Indeed, banks can be defined as firms that maximize profits by managing risks. Paradoxically, it has been recognized that "the risk/reward relation has not yet been analysed on an industry level or on a macroeconomic level" [Scholtens and Van Wensveen (2000: p. 1247)].
Banks have specific characteristics that differentiate them from other firms. Banking objectives are multiple and include risk management and profitability ones. Banks need to achieve these objectives because of the existence of default, liquidity and market risks. Furthermore, given the non competitive features of banking markets, profitability becomes a survival condition for the intermediaries. Banks manage their assets to maximize profits by seeking the highest returns possible on loans and securities while at the same time trying to lower risk and making adequate provisions for liquidity. Thus the risks, tradeoffs and outcomes of the intermediation process are defined by risk management and profitability objectives.
Paradoxically, the joint study of risk management and profitability objectives is relatively new in the literature. This situation occurs because they are not necessarily compatible ones. Usually, the management of liquid reserves implies opportunity costs associated to the loss of lending and investment opportunities. Profitability reductions are almost inevitable due to these costs. Furthermore, risk management practices consume resources and cash flows, but they do not increase profitability (they only reduce the variability of expected cash flows). Indeed, the rationales of risk management are not related to banking profitability.3 Such situation explains why banking decisions frequently involve time-consistency dilemmas and tradeoffs.
The complexity of the decision making process explains why, until recently, little economic theory has been developed to explain the behavior of banks. Banking decisions pursue multiple and competing objectives under uncertainties regarding the management of liquidity, assets and liabilities. Such decisions involve risks and value tradeoffs difficult to assess. However, among theorists, there is a consensus that intermediaries behavior may be understood through the analysis of their risk management practices [Scholtens and Van Wensveen (2000) and Allen and Santomero (2001)]. Such situation explains why the study of risk management is one of the most interesting research fields among financial economists.
Here we analyze the behavior of a monopolistic bank that acquires liabilities (deposits) to manage their assets (short-term reserves and long-term loans).4 We build a banking-firm model to study the decisions that a bank takes to achieve risk management and profitability objectives. Banking decisions refer to deposits and reserves. The bank faces liquidity and solvency risks because loans may not be repaid (default risk) and because unexpected deposit withdrawals may occur (liquidity risk). In our model, bankruptcy costs rationalize risk management practices. The existence of uncertainties in both sides of the balance sheet justifies them. We refer to our model as an AssetLiability-Management (ALM) one.
The ALM banking model pursues to explain intermediaries' behavior on the assumption that "compromise solutions" are necessary given the existence of conflicting risk management and profitability objectives. Such solutions are necessary due to the impossibility of optimizing all the objectives at the same time. From a risk management perspective, such solutions are necessary to manage liquidity, assets and liabilities. The uncertain behavior of depositors (liquidity risk) and the risks attached to the banks' portfolio investment (default risk) justify the need of such solutions. From an economic perspective, such solutions are necessary to guarantee the provision of liquidity services, the transformation of assets and the maximization of profits.
We develop the banking analysis in two steps. The first one involves the description and extension of the framework of Bougheas and Ruiz-Porras (2008). We use this framework to define the banking decision-making problem. We define this problem in terms of the existence of uncertainties, the availability of liquidity management strategies and the conditions that guarantee the viability of the asset transformation process. The second step focuses on the resolution of the banking program assuming a monopolistic intermediary. Particularly, the program involves the numerical calibration of solutions using two decision variables: reserves and deposits. Such estimations allow us to study the comparative-static qualitative effects on the banking decisions.
The ALM model seems to explain and justify traditional banking practices. Specifically, the calibration exercises confirm that compromise solutions are necessary to deal with the time-consistency dilemmas and tradeoffs between liquidity risk management and profitability objectives. They also suggest that asset management practices effectively contribute to increase profits through the acquisition of assets with an acceptable level of risk. The model also shows that liability management practices and market power support banking profitability. Furthermore, the ALM model confirms that banks should undertake long-term risky investments when depositors trust the viability of the asset transformation process.
Theoretically, the ALM banking firm model is the counterpart of the traditional liquidity insurance and financial fragility models in which depositors play the main role. Specifically, the model provides further elements to assess the relationships among ALM practices, multiple uncertainties and monopolistic behavior. It complements the study of Gonzalez-Hermosillo and Li (2008) that focuses on the relationships among market, credit and liquidity risks. It also complements the study of Khemraj (2010) that focuses on the effects of liquidity preference on the loan market assuming default risks. Furthermore, the model extends the one of Bougheas and Ruiz-Porras (2008) to study the effects of simultaneous decisions regarding reserves and deposits.5
]]> The paper is divided in nine sections. The second reviews the literature. The third describes the basic ALM framework developed by Bougheas and Ruiz-Porras (2008). The quarter shows the trade-offs and time-consistency dilemmas involving the risk management and profit maximization objectives. The fifth focuses on the conditions necessary to define the inter-temporal liquidity-solvency function. The sixth extends the analysis to the viability of the asset transformation process. The seventh describes the banking regimes that define the optimization problem. The octave solves the problem numerically. The final section concludes. The appendix includes the decision-making banking problem and an explanation of the computational algorithm used for solving it.
Literature review
The industrial organization approach to banking aims at explaining the behavior of banks. Traditionally, the Monti-Klein model is the reference framework under this approach [Freixas and Rochet (2008)]. The main assumption of this model is that the banking system is a monopolistic one. Thus, in the model, the bank is an entity that optimally reacts to its environment. Particularly, the bank confronts a demand for loans and a supply of deposits that are deterministic. We emphasize these assumptions be-cause one of the main results of the model is the separability property: The optimal deposit rate is independent of the characteristics of the loan market, and the optimal loan rate is independent of the characteristics of the deposit market.
The separability property is one of the most controversial results in banking economics. Financial regulators explicitly assume that this property does not hold. Otherwise, many regulations practices would be useless. Theoretically, several banking firm models have been developed to justify why this property may not hold. Among these models are the ones of Dermine (1986) and Prisman Slovin and Sushka (1986). The first model introduces risky portfolio investment. The second model allows for random deposit withdrawals. These models are important because they show that risk and uncertainties can invalidate the separability property. Moreover they provide elements to justify that banking decisions must take into account risks and uncertainties.
Paradoxically, many behavioral banking studies do not necessarily focus on the impacts of risk and uncertainties. Indeed many researchers recognize that further efforts are necessary to explain banking behavior and banking decisions. There is a consensus around the necessity to "move further in constructing a theory of financial intermediation that can explain the day-to-day operations of financial institutions and markets and their role within the real economy" [Scholtens and Van Wensveen (2000: p. 1249)]. Apparently, the main limitations of current theories refer to the difficulties to include banking specificities (associated to the existence of risk, uncertainties and non competitive markets). Some theories simply ignore them for modeling purposes.6
Some recent behavioral studies have analyzed the behavioral implications of banks' specific characteristics. Among them we include the ones of Bougheas and Ruiz-Porras (2008), Gonzalez-Hermosillo and Li (2008) and Khemraj (2010). The first one focuses on how banking decisions must take into account the likelihood of liquidity and solvency risks to guarantee the short and long-term viability of the asset transformation process. The second one focuses on how market, credit and liquidity risks affect banking decisions. The third one studies the effects of liquidity preference on the loan market assuming default risks. These studies are relevant because they analyze banking behavior assuming risk management and profitability objectives.
These theoretical studies are not only complementary, but also share several common features. Theoretically, the three studies analyze banking behavior with variations of the Monti-Klein framework. They assume that banks have simultaneous risk management and profitability objectives that may not be fully compatible. They also assume the existence of certain degree of uncertainties. Moreover, in all cases the final banking outcomes depend on the relationships among risks, measured by certain parameters, and the banking decisions. Methodologically, given the complexity of the decision-making problems, the three models are solved and analyzed with numericallybased algorithms. The economic analysis mainly relies on calibration results.
Here we analyze the behavior of banks with a model that shares the features described above. Specifically, we extend the model of Bougheas and Ruiz-Porras (2008) to study the effects of banking decisions regarding reserves and deposits on the likelihood of liquidity and solvency risks. Our ALM banking model complements the previous studies because it explicitly focuses on the relationships of short and long term among ALM practices, multiple uncertainties and monopolistic behavior. Furthermore, our banking firm model is the counterpart of the traditional liquidity insurance and financial fragility models in which depositors play the main role.7 We believe that these clarifications are important in order to contextualize our research.
]]> The banking model from an ALM perspective
In this section, we describe our microeconomic framework keeping in mind that banking risk management involves several objectives. The first one is to make sure that the bank has enough reserves to pay its depositors when there are deposit withdrawals (liquidity management). The second one relates to the acquisition of assets with an acceptable return and an acceptable low level of risk (asset management). Another objective relates to the acquisition of funds with a low cost (liability management). Here we take into account these risk management objectives to build the structure of the banking model from an ALM perspective. By the moment we will not consider the monopolistic structure prevailing in the banking system.
Assume a three period framework (T=0,1,2). At T=0, the monopolistic bank allocates its deposits D between liquid reserves, R (money), and illiquid portfolio investments, L (loans and securities), to maximize long-term expected profits. The decision variables are deposits and reserves. In making these asset decisions, the bank takes into account elements of uncertainties on both sides of its balance sheet: A liquidity shock will affect the demand for withdrawals by depositors at T=1, while the return on the bank's portfolio investments remains unknown until T=2. On the liabilities side, we assume that the proportion, x, of deposits withdrawn at T=1 is a random variable with support on [0,1] and density function f(x). Those depositors that withdraw at T=1 receive the amount that they have invested, xD, while those depositors that wait until T=2 to withdraw their funds receive (1-x)rD, where r>1.8 On the assets side, we assume that the bank's investment portfolio offers a gross return, y, that is a continuous random variable with support on [0,Y], density function g(y) and E(y)>1. We have set an upper bound on the support of the distribution since the bank's portfolio consists of loans and securities that have the characteristics of debt contracts. In addition, the bank's net return on reserves is zero.
We assume that the bank has available contingent strategies to manage liquidity shortages and surpluses. We introduce costly liquidation to allow the bank to honor its obligations with depositors in the case of unexpected liquidity shortages (xD>R). In such case, at T=1 the liquidation value of a unit of portfolio investment is equal to 1/c (c>1).9 As long as shortages are sufficiently small, the bank will be able to meet the demand for withdrawals at the cost of reducing its long-term profitability. Thus the bank can ensure the viability of the asset transformation process by holding a sufficiently high amount of reserves. When there are surpluses (xD<R), excess reserves yield a low return relative to portfolio investments. Therefore, liquidity surpluses can also threat the asset transformation process because they increase the risk that the value of the final assets will not match the bank's long-term liabilities.
Risk management objectives contribute to explain the behavior of the intermediaries. In order to rationalize such objectives, we introduce bankruptcy costs. More specifically, we assume that when the bank fails, it incurs a loss of size B. Such fixed costs are independent of the specific cause of failure. The bank can fail either because of lack of liquidity at T=1 or because of insolvency at T=2. In the absence of bankruptcy costs, the bank would maximize expected returns ignoring any risk arising by its decisions. However, bankruptcy costs introduce non-convexities in its payoff and, as a result, the bank acts in a risk-averse manner. For simplicity, we assume that both types of bankruptcy costs, short-term and long-term ones, are identical. Thus, we can redefine risk management objectives in terms of the minimization of bankruptcy costs. Finally, we assume that bank owners are protected by limited liability.
Liquidity management: trade-offs and time-consistency dilemmas
Liquidity management refers to the bank's choice of its level of reserves. Reserves (R=D-L) are held to cope with early deposit withdrawals at T=1. As we have indicated, the monopolistic bank faces a trade-off when it makes this choice. A too low level of reserves and the bank risks failure at T=1 because of being unable to meet the demand for early withdrawals. A too high level of reserves and the bank risks insolvency at T=2 because of being unable to meet the demand for late withdrawals. This is the first tradeoff involving risk management and profitability objectives. Let xR denote the threshold level of the proportion of deposits withdrawn at T=1 that exactly matches the ratio of reserves to deposit outflows. The banking threshold level xR is:

If the realized value of x is equal to xR then the levels reserves and payments to early depositors will be identical and long-term banking outcomes will only depend on portfolio investment.
]]> Liquidity decisions and risk management practices are closely related. If the initial reserve provision of the bank does not match the level of early withdrawals (liquidity risk), the availability of contingent liquidity strategies must be considered. Inadequate reserve provisions can be managed through the costly liquidation of illiquid assets while reinvesting remaining reserves is the option for liquidity surpluses. When the realized proportion of early withdrawals is higher than the threshold value, x>xR, there is a liquidity shortage, R-xD<0. In the opposite case, when x<xR there is a liquidity surplus, R-xD>0, and the excess reserves are held until the last period. Let S denote the difference R-xD.The traditional financial fragility literature assumes that deposit withdrawals may cause banking failure. Here we show how this event can occur. Let xL be the value of x such that L-c(xLD-R)=0. In words, when the proportion of deposits withdrawn at T=1 is equal to xL, the liquidation value of the bank's portfolio is equal to the liquidity shortage. Solving for xL we get
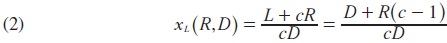
If x>xL the bank will not be able to meet the demand for withdrawals and it will fail because of lack of liquidity. The asset transformation process ends because liquidity requirements exhaust the banking assets (early termination). In this context, the liquidity risk management objective competes against and profitability one and compromise solutions are necessary.
Finally, we should emphasize that liquidity risk management and profit maximization objectives may involve other time-consistency dilemmas. When there is a surplus, revenues at T=2 will be augmented by the corresponding excess reserves. When there is a shortage, the portfolio investment will be reduced by cS. The provision of liquidity for the short-term by holding reserves has a negative effect on future profits because it reduces investment. However, inadequate liquidity provision does not only increase the risk of illiquidity at T=1 but also reduces future profits because of the liquidation of investment. These dilemmas between short-term and long-term banking objectives have been described, among others, by Mishkin (2007).
Profitability, liquidity and solvency
The liquidity management decisions adopted by the bank together with the realized return of its portfolio investment determine the financial status (liquid, illiquid, solvent and insolvent) of the bank and, conditional on being solvent at T=2, its level of profits. From a microeconomic perspective, the maximization of long-term profits is the main objective of the banking firm. Profits are given by:
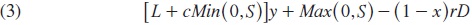
The first-term captures the bank's portfolio return. Notice that in the case of a shortage (S<0), the investment is reduced by the amount of liquidation. The second term shows the level of excess reserves when there is a surplus (S >0) and the last term shows the total promised payments to those depositors that withdraw their funds at T=2.
]]> We should point out that a liquidity management policy that excludes the possibility of financial failure does not exist. If the bank does not make any portfolio investment (R=D) it will never fail because of lack of liquidity but since r>1 it will become insolvent with certainty as long as x<1. It is also clear that insolvency cannot be avoided for any R<D since the probability that y is less than the gross return on reserves, which is equal to 1, is strictly positive.The avoidance of failure due to liquidity problems does not guarantee long-term profitability. Given that x<xL, i.e. the bank did not fail at T=1 because of liquidity problems, it can still fail at T=2 because of insolvency if y is below a threshold level that we refer to as the bank solvency threshold. When at T=2 the return on its portfolio investment is below this threshold, the value of its portfolio will be less than its liabilities. However, given that these liabilities depend on the realization of x, i.e. the demand for early withdrawals, and the bank's liquidity management decisions, we need to evaluate bank solvency threshold values for both liquidity shortages and liquidity surpluses. Let yS-and yS+ denote the corresponding threshold values. These thresholds will depend on R and D, the bank's liquidity management decisions, and x, the proportion of deposits withdrawn at T=1.
To obtain the threshold yS-(x,R,D) that determines the value of y such that bank profits vanish, for given initial deposits and their allocation between reserves and portfolio investment, and conditional on a liquidity shortage and the realized demand for early withdrawals, set (3) equal to zero and solve for y:
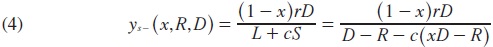
where S=R-xD<0.
In a similar way, we obtain the threshold yS+(x,R,D) that determines the value of y such that bank profits vanish conditional on a liquidity surplus:
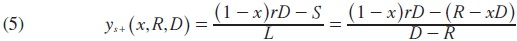
where S=R-xD >0.
Thresholds (4) and (5) jointly define an inter-temporal liquidity-solvency relationship. Given the levels of deposits and reserves there is a threshold value of y such that bank profits vanish for each x. Notice that in the benchmark case where x=xR, i.e. the demand for early withdrawals exactly matches the level of reserves the threshold level is given by the ratio of long-term obligations to portfolio investment. For both thresholds the value is r.
]]> Viability of the asset transformation process
We have found that the bank can fail either because of liquidity problems at T=1 or because of insolvency at T=2. These are the traditional causes of bank failure. Previously, Bougheas and Ruiz-Porras (2008) have identified a third reason. Such reason relates to the viability of the asset transformation process. In the previous section, we have shown the bank solvency thresholds that identify minimum values for the bank's portfolio return that are consistent with bank solvency. These thresholds values depend on the bank's choice of its level of deposits, the bank's liquidity management decisions and the realized early demand for withdrawals and therefore their exact values become known at T=1. However, given that the bank's portfolio return is bounded from above, if these thresholds are larger than the maximum return then at T=1 it will be known with certainty that the bank will be insolvent at T=2. In such cases, the bank fails be-cause the long-term asset transformation process is not viable.
We analyze the viability of the asset transformation process by considering the cases of liquidity shortages and surpluses. We consider first the case of liquidity shortages. Using (4) we find that
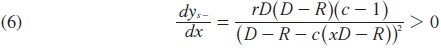
The higher the realized value of the proportion of deposits withdrawn early, the larger the shortage will be that implies a higher proportion of portfolio investment will be liquidated. Then, since both c and r are higher than 1, the higher the return on the bank's portfolio investment needs to be in order for the bank to be able to honor its long-term obligations. By setting the left-hand side of (4) equal to Y, the upper bound of the support of the portfolio return's distribution, we derive a cut-off value for x, denoted by xS-, such that for realized values of the proportion of early withdrawals higher than this cut-off, the asset transformation process fails to be viable.

Notice that the asset viability transformation condition is stricter than the liquidity one when xS-<xL. In other words, a bank that fails at T=1 because of illiquidity problems also fails because its asset transformation process is not viable. This would suggest that we only need to concentrate on the viability of the transformation process since the bank's payoff, when it fails, is independent of the cause of failure. However, we will examine these two cases separately. When the liquidity constraint is not satisfied, the bank's only option is to liquidate its portfolio investment to satisfy the demand for liquidity. In contrast, when only the viability constraint is not satisfied there are two alternatives. The bank can either be liquidated at T=1 and distribute the proceeds to those depositors that were planning to withdraw their funds late or wait until T=2 for its investments to mature and then distribute the proceeds to the same depositors. In both cases, late depositors will receive less than what they were promised and the option followed will depend on the expectations at T=1 about the performance of the bank's portfolio.
Now, we consider the case of surpluses. Using (5) we find that

The lower the realized value of the proportion of deposits withdrawn early, the higher excess reserves will be. But since the gross return on excess reserves is 1, which is less than the gross interest rate offered on deposits, r, the higher the return on the bank's portfolio investment needs to be in order for the bank to be able to honor its long-term obligations. By setting the left-hand side of (5) equal to Y, the upper bound of the support of the portfolio return's distribution, we derive a cut-off value for x, denoted by xS+, such that for realized values of the proportion of early withdrawals lower than this cut-off, the asset transformation process fails to be viable.
]]>
Since Y>r>1 if r is sufficiently close to the 1, i.e. the gross return on reserves then the above ratio will be negative and the transformation process will be viable with certainty.
The above analysis shows that because illiquidity and insolvency are intertemporally linked, these two causes of bank failure must be considered together. Either a too high or a too low level of liquidity provision can cause the bank to fail because they reduce the chances that the bank will be able to meet its obligations to depositors. This third cause of banking failure, as pointed out by Bougheas and Ruiz-Porras (2008), is relatively new in the literature.
Banking regimes
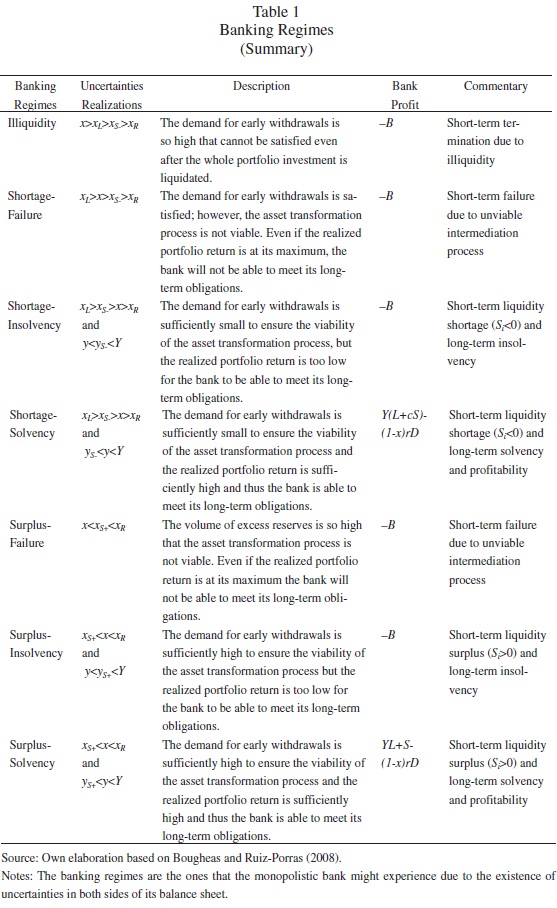
The bank's performance depends on its choice of the level of deposits, on its liquidity management decisions, on the realization of the demand for early withdrawals and, given that at T=1 the viability of the asset transformation process is assured, on the realization of its portfolio return. The various threshold levels derived in the previous sections define 7 banking regimes related to the short-term and long-term status of the bank's balance sheet. The first 4 scenarios correspond to the case of a shortage of reserves at T=1 while the last 3 correspond to the case of a surplus of reserves. Table 1 summarizes the banking regimes.
Optimal banking policies with multiple objectives
]]> The monopolistic bank must make ex-ante choices based on how each possible action affects the risk management and profit maximization objectives. The decision variables are the level of reserves R and total deposits D. Thus, the bank has to choose D and R to maximize the function
The first double integral is equal to expected profits in the Surplus-Solvency regime, the second integral is equal to expected profits in the Shortage-Solvency regime, and the last expression is equal to expected losses given that the bank has failed in the remaining regimes.10
We should point out that the decisions of monopolistic bank are also constrained by the features of the deposit market. The choice of the level of deposits determines the scale of banking activities (measured by total liabilities) and the long-term deposit return r=r(D). The higher the deposit return, the higher level of deposits available for the bank. Thus banking behavior and the decision-making process are constrained by the supply behavior of the depositors. Here we assume a constant-elasticity depositsupply curve,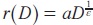 , to describe such behavior. Such assumption allows us to analyze the effects of changes in the sensitivity of the supply of deposits to long-term deposit returns.
, to describe such behavior. Such assumption allows us to analyze the effects of changes in the sensitivity of the supply of deposits to long-term deposit returns.
Mathematically, the banking problem not only requires compromise solutions due to the existence of competing objectives and market constraints, but also a criterion for decision-making under uncertainties. Assets and liabilities are uncertain as long as f(x) and g(y) are unknown. Here we adopt the Laplace criterion to deal with uncertainties in both sides of the balance sheet (i.e. we assume that f(x) and g(y) are uniform density functions). Furthermore, for simplicity, we use the two-dimension Brent-Powell algorithm to find the ex-ante optimal R and D decisions for equation (10).11 We use such algorithm because the first-order derivatives of the banking problem are mathematically complex and difficult to interpret from an economic perspective. Finally, for estimation purposes, we allow the benchmark parameter values to be: a= 1.1, B = 2, c =1.5,ε = 2,Y = 10 .
We investigate the comparative statics of the model with several calibration exercises of the banking decision problem.12 The absence of a closed form solution for the banking problem makes difficult to analyze the qualitative behavior of the model analytically. Particularly, we estimate the optimal banking decisions, the long-term deposit return, the optimal asset allocation and the expected banking profits. The numeric calibrations suggest consistent behavioral patterns on the optimal decisions associated to changes in the parameters. Such patterns allow us to determine the qualitative comparative-static effects. We summarize such effects in Table 2.
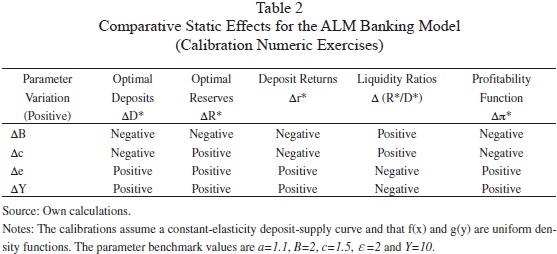
Table 2 shows consistent patterns assuming the existence of ALM practices, multiple uncertainties and monopolistic behavior. Calibrations show that increases in bankruptcy or liquidation costs and decreases in the deposit-supply elasticity or in the quality of investment may increase liquid reserves. They also show that the same variations in the parameters may reduce the availability of deposits, the deposit return and banking profitability. Furthermore, the calibration exercises show tradeoffs between the short-term management of liquidity and long-term profits. Indeed, the parametrical variations show that qualitative effects are the opposite ones for the liquidity ratios and the profitability variable. Thus compromise solutions are always necessary.
]]> The calibrations confirm that asset management practices enhance banking profits. Intuition suggests that as the quality of long-term investment improves, lower reserves will be necessary to defend the bank against random deposit withdrawals. Calibrations reflect this behavior. Notice that as long as the mean quality of the long-term investment portfolio Y increases, long-term investment increases. Moreover, acceptable levels of risk and asset diversification avoid reductions on long-term investment earnings. This intuitively explains why liquidity ratios cannot increase and why profits increase when investment returns increase in the banking models.The exercises also confirm that liability management practices enhance banking profits. The practice of setting targets for asset growth through the expansion of liabilities issue is explained in our models due to the presence of risks. Conventionally, this practice relies on the belief that liability management provides sources of funding and liquidity to support profitability. The models suggest that this makes sense. The models' prediction, that reserve/deposit ratios will decrease when elasticity increases, reflects what happens in practice. In the US banking system, it has been considered that liability management practices have increased the proportion of banking assets held in loans, "from 46 por ciento of bank assets in 1960 to 66 por ciento in 2005" [Mishkin (2007: p. 231)].
The model confirms that non competitive practices may strength the relationship between liability management practices and profitability. Notice that the model predicts that increases in the deposit-supply elasticity increase profits. We can explain this prediction on the basis that the bank recognizes its power over the deposit market. Market power allows the bank to reduce its liability costs and simultaneously to increase its profits.
However, banking decisions are constrained by the supply behavior of the depositors (i.e. by the deposit-supply elasticity). When the sensitivity of depositors is small, the return necessary to increase deposits must be high. High financing costs directly reduce profits. Thus, increases in such elasticity must imply increases in banking profits.
We summarize our findings by indicating that the ALM model seems to explain traditional banking practices. Specifically, the calibration exercises confirm that compromise solutions are necessary to deal with the time-consistency dilemmas and tradeoffs between liquidity risk management and profitability objectives. They also suggest that asset management practices effectively contribute to increase profits through the acquisition of assets with an acceptable level of risk. The model also shows that liability management practices and market power support banking profitability. Finally, the ALM model confirms that banks should undertake long-term risky investments when depositors trust the viability of the asset transformation process.
Conclusions and discussion
We have analyzed the decisions that a monopolistic bank takes to achieve risk management and profitability objectives. The ALM banking model pursues to explain intermediaries' behavior on the assumption that "compromise solutions" are necessary and that contingent liquidity risk management strategies are available. In the model, the bank faces liquidity and solvency risks because loans may not be repaid and be-cause unexpected deposit withdrawals can occur. Furthermore, it is constrained by the features of the deposit market. Thus, banking decisions refer to deposits and reserves. Methodologically, given the complexity of the decision-making problem, the model is solved and analyzed with calibration exercises.
The ALM banking model shows consistent patterns assuming the existence of ALM practices, multiple uncertainties and monopolistic behavior. Calibrations show that in-creases in bankruptcy or liquidation costs and decreases in the deposit-supply elasticity or in the quality of investment may increase liquid reserves. They also show that the same variations in the exogenous parameters may reduce the availability of deposits, the deposit return and banking profitability. Furthermore the calibration exercises show tradeoffs between the short-term management of liquidity and long-term profits. Indeed, the same parametrical variations show that qualitative effects are the opposite ones for the liquidity and profitability variables.
The ALM model seems to explain traditional banking practices. Specifically, the calibration results confirm that compromise solutions are necessary to deal with the time-consistency dilemmas and tradeoffs between liquidity risk management and profitability objectives. They also suggest that asset management practices effectively con-tribute to increase profits through the acquisition of assets with an acceptable level of risk. The model also shows that liability management practices and market power support banking profitability. Finally, the ALM model confirms that banks should undertake long-term risky investments when depositors trust the viability of the asset transformation process.
]]> We believe that the main contributions of the model relate to the behavioral analysis considering banking specific characteristics. Particularly, these contributions focus on the issues related to: (1) The clarification of the nature of risk management and profitability objectives, (2) the analysis of the relationships between liquidity and solvency risks, (3) the identification of optimal solutions for reserves and deposits, and (4) the development of decision-making guidelines. Methodologically and theoretically, as indicated before, our model complements the ones of Bougheas and Ruiz-Porras (2008), Gonzalez-Hermosillo and Li (2008) and Khemraj (2010). Furthermore, it also complements the study of Gamba and Triantis (2010).13Finally, we should point out that further theoretical developments on banking behavior may be achieved by combining economic theory and multi-criteria optimization techniques. Optimization problems characterized by competing objectives, compromise solutions and multiple uncertainties usually are analyzed by specialists in operations research. Banking specialists may take advantage of such techniques to improve their decision-making processes. Thus, further collaborative studies seem necessary.14 We believe that an additional contribution of our study is to justify the necessity of such interdisciplinary work. Collaborations may be necessary to improve our knowledge on the management of financial institutions.
References
Allen, F. and A. M. Santomero (2001). "What do intermediaries do?", Journal of Banking and Finance, 25(2), 271-294. [ Links ]
Allen, F. and A. M. Santomero (1997). "The theory of financial intermediation", Journal of Banking and Finance, 21(11-12), 1461-1485. [ Links ]
Bougheas, S. and A. Ruiz-Porras (2008). "Administración de los problemas financieros de los bancos. Dilema entre los riesgos de liquidez y solvencia", El Trimestre Económico, 75 (Special issue), 215-233. [ Links ]
]]>Dermine, J. (1986). "Deposit rates, credit rate and bank capital: The Klein-Monti model revisited", Journal of Banking and Finance, 10(1), 99-114. [ Links ]
Freixas, X. and J. C. Rochet. (2008). Microeconomics of Banking, Second edition, Cambridge, United States, The MIT Press. [ Links ]
Gamba, A. and A. J. Triantis (2010). "Disintegrating risk management", Maryland, United States, University of Maryland-Robert H. Smith School of Business, Working Paper RH-06-106. [ Links ]
Gonzalez-Hermosillo, B. and J. X. Li (2008). "A banking firm model: The role of market, liquidity and credit risks" in E. J. Kontoghiorghes, B. Rustem and P. Winker (eds), Computational Methods in Financial Engineering, (Springer Verlag, Berlin-Germany), 259-271. [ Links ]
Khemraj, T. (2010). "What does excess bank liquidity say about the loan market in Less Developed Countries?", Oxford Economic Papers, 62(1), 86-113. [ Links ]
]]>Mishkin, F. S. (2007). The Economics of Money, Banking and Financial Markets, 8th edition, Boston, United States, Addison Wesley. [ Links ]
Press, W. H. et al. (1992). Numerical Recipes in C. The Art of Scientific Computing, 2nd ed., New York, United States, Cambridge University Press. [ Links ]
Prisman, E. Z., M. B. Slovin and M. E. Sushka (1986). "A general model of the banking firm under conditions of monopoly, risks and recourse", Journal of Monetary Economics, 17(2), 293-304. [ Links ]
Scholtens, B. and D. van Wensveen (2000). "A critique on the theory of financial intermediation", Journal of Banking and Finance, 24(8), 1243-1251. [ Links ]
Zopounidis, C. (1999). "Multi-criteria decision aid in financial management", Euro-pean Journal of Operational Research, 119(2), 404-415. [ Links ]
]]>Zopounidis, C. and M. Doumpos (2002). "Multi-criteria decision aid in financial decision making: Methodologies and literature review", Journal of Multi-Decision Making Analysis, 11(4-5), 167-186. [ Links ]
1 The author gratefully acknowledges the suggestions and comments by Spiros Bougheas (University of Nottingham), Nancy García-Vázquez (El Colegio de Jalisco) and two anonymous referees of EconoQuantum. Without doubt, their contributions have significantly improved the paper. However, the usual disclaimer applies.
3 The rationales for risk management in the context of intermediaries include bankruptcy costs, managerial self-interest, non-linear taxes and capital market imperfections. See Gamba and Triantis (2010) for a survey.
4 The assumption of perfect competition seems not really appropriate in banking. Usually there are important barriers to entry in the borrowing and lending markets. Here we consider a monopolistic banking system following the traditional Monti-Klein approach for analyzing behavioral issues. However, we should recognize that an oligopolistic competition model may be more appropriate for modeling purposes.
5 Bougheas and Ruiz-Porras (2008) assume that the level of reserves is the only decision variable.
6 Indeed it has been argued that "many current theories of intermediation are too heavily focused on functions of institutions that are not longer crucial" [Allen and Santomero (1997:1461)].
7 See Freixas and Rochet (2008) for a review of the financial fragility literature.
]]> 8 Following the traditional financial crisis literature, we assume that at T=0 when depositors invest their funds at the bank, they are uncertain about when they will need to make withdrawals. Nevertheless, they understand that only if they keep their funds at the bank until T=2 they will receive the higher return.9 These liquidation costs are related to selling securities, calling in loans and selling off loans.
10 Notice that the function of banking preferences (10) has economic interpretation. Assuming that the bank is risk-neutral and that density functions are known, the function is equal to expected profits.
11 The Brent-Powell algorithm locates relative minima of functions with one or more variables. It uses a starting point (initial guess) to search for the path of steepest descent of the function. Here we use such algorithm on the basis that the maximization of π(R,D) is equivalent to the minimization of -π(R,D). We have applied the algorithm at different starting points to verify the consistency of the numeric solutions of each calibration exercise. We have used such procedure to guarantee the robustness of the numerical findings and to distinguish between local and global maxima. See the Appendix for a description of the banking problem and an explanation of the Brent-Powell algorithm.
12 We use the MATHEMATICA software to estimate the calibrations of the microeconomic banking problem.
13 Gamba and Triantis (2010) analyze the effects of coordination, liquidity management, and hedging with derivatives with a dynamic structural model.
14 See Zopouinidis (1999) and Zopouinidis and Doumpos (2002) for literature surveys on applications of multicriteria analysis to financial decisions.
]]>