
Numerical Simulation of the Behaviors of the Bray–Liebhafsky Oscillating Chemical Reaction by a Four–variable Model
Jie Ren, Jinzhang Gao,* and Wu Yang
College of Chemistry & Chemical Engineering, Northwest Normal University, Lanzhon, 730070, PR China. *jzgao@nwnu.edu.cn
Received November 18, 2011. ]]> Accepted February 10, 2012.
Abstract
Based on a ten–step chemical model involving the concentrations of I2(aq), O2(aq), and the intermediates of I– and HIO2, four independent variables and seven irreversible steps, the nonlinear behavior of Bray–Liebhafsky (BL) oscillating reaction was investigated. The results showed that with different values of initial concentrations of reactants in the process of simulation, both periodic oscillation and chaotic behavior could be observed. In addition, at the same initial concentrations and rate constants, the system becomes more and more regular after being chaos. That is to say, the translation from chaos to periodic oscillation at the same initial conditions appeared in the BL system. The nonlinear behavior of system was also investigated briefly.
Key words: Numerical simulation; Bray–Liebhafsky oscillating chemical reaction; chaos.
Resumen
En base a un modelo químico de diez pasos que involucra las concentraciones de I2 (ac), O2 (ac), los intermediarios de I– y HIO2, cuatro variables independientes y siete pasos irreversibles, fue investigado el comportamiento no lineal de la reacción oscilatoria de Bray–Liebhafsky (BL). Los resultados mostraron que con valores diferentes de concentraciones iniciales de los reactantes en el proceso de simulación, tanto la oscilación periódica como el comportamiento caótico pudieron ser observados. Además, a la misma concentración inicial y constantes de velocidad, el sistema se convierte en más regular a partir del caos. Es decir, la traslación del caos a la oscilación regular en las mismas condiciones iniciales aparece en la Reacción BL. El comportamiento no lineal del sistema también fue estudiado resumidamente.
Palabras clave: Simulación numérica, reacción química oscilante Bray–Liebhafsky, caos.
]]> Introduction
In 1921 Bray [1] firstly observed a homogeneous batch oscillating chemical reaction involving the iodate–catalyzed decomposition of hydrogen peroxide in acidic solution. Subsequently, further studies were performed by Liebhafsky so that the system was commonly named as Bray–Liebhafsky (BL) oscillating chemical reaction [2]. The overall chemical change in the BL system can be described below,

This process occurs via the autocatalytic reaction of iodate and peroxide, overall process B and overall process C.

In this system, oscillations in the concentration of iodine, iodide and oxygen existed Edelson and Noyes [3] proposed a detail mechanism including 18 elementary reactions with rate constants, and pointed out theoretically the intermediates such as I2, O2, I–, I•, HOI, HIO2 and HOO•. However, they have not confirmed whether the rate of oxygen escape is proportional to the degree of supersaturation or not. That is to say, the system is very sensitive to change in concentration of dissolved oxygen. Lately, Treindl and Noyes [4] proposed a skeleton reaction mechanism that H2O2 oxidized no other iodine–containing species than iodide ion, even though H2O2 was the only oxidant in the overall stoichiometry for one of the two main processes of the BL reaction. Schmitz [5] considered that oxygen was not a necessary part of the explanation of oscillations in the BL reaction. In addition, the chemical effects of oxygen resulted mainly from the oxidation of iodide by radical processes and the release of oxygen also had physical on the whole process. Recently, some kinetic characteristics of the hydrogen peroxide oxidation of iodine to iodate were studied by Schmitz [6]. In addition, the influences of molybdate on the BL oscillating chemical reaction [7, 8] were qualitatively explained by the mentioned skeleton mechanism, and the production of singlet oxygen (1O2) by the disproportionation of hydrogen peroxide catalyzed by molybdate [9, 10] was also investigated in detail.
Although a large number of works [11–14] devoted to the mechanism of the BL reaction for a long time, the overall mechanism has still not been elucidated, and is complicated by the fact that the system is also sensitive to light [15], pressure and stirring [16, 17], microwaves [18, 19] and oxygen [20, 21]. It seems to be too difficult to obtain enough relevant information on the kinetics of this system. All suggestions reflect that the nonlinear phenomena are so complex that they should be investigated by various ways.
The simulation by mathematics is a simple and effective approach to display the character of nonlinear phenomena for a complex system. In our previous work [22], the concentrations of I2(aq) and O2(aq) were simulated by involving a two variable model. In order to investigate the BL system more detailed, a four–variable model was used, in which the concentrations I2(aq) and O2(aq), and the intermediates such as I– and HIO2 were also calculated by mathematical calculation after proper simplification and modification of the mechanism.
Results and discussion
]]> ResultsAt peculiar conditions, the concentration of HIO2, I–, I2 and O2 change periodically in the batch system showing in Figure 1. The rate constants for calculation are listed in Table 1. Figure 1e (i.e., the trajectory of phase space) and the Largest Lyapu–nov Exponent (λL = 0.1134) showed that simple oscillations are observed. In order to investigate the effect of the initial concentrations on the behavior of the system, different initial concentrations of the system are adopted in the process of simulation. The results show that the behaviors of the system are different at different initial concentrations and chaotic behavior is observed in the BL oscillating chemical system (as shown in Figure 2). The separated trajectories of the phase space in Figure 1e are replaced by trajectories twined in Figure 2e. This indication of chaos is confirmed by the Largest Lyapunov Exponent (λL = 0.7269). The fact makes it clear that with changing of the control parameter, the system translates from one state to another (from periodic oscillation to chaos).

Figure 3 showed comparison the calculated results with the one from experiment [4]. The simulated behaviors were qualitatively consistent with experimental observations basically. However, the inconsistencies exist in the simulation shapes, such as the whole oscillation curve shifts slowly with time. The main reason may lie in that the experimental process is not like theoretical calculation one, effect by many factual operation conditions, such as the temperature fluctuates slightly and major reactants consume slowly but continuously. In consequence, the reaction continuously flows in the direction of decreasing free energy and the overall reaction is always moving inexorably towards the chemical equilibrium state and there is no oscillation appearing.

Discussion
The effect of α on the BL nonlinear behavior
The simulation results show that only when a is ranging from 0.75 to 0.0001, the above differential equations exist periodic solution. That is to say, the periodic oscillation can be observed only as a in this range. In addition, with the increasing of a, the period of the system increased obviously (as shown in Figure 4). As mentioned above,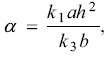 so the effect of a on the system's behavior can be discussed from both rate constants and initial concentrations. All components match each other very well in the complex nonlinear system, once one of them out of a certain range, the whole behavior of the system will change tremendously. Occasionally the system will translate from one state to another. HIO2, a very important intermediate producing from R1 is also the reactant of R3. So k1ah2 is relative to the total producing rate of HIO2. The bigger value of k1ah2, the more HIO2 produces in R3. As the results, the time of the concentration of HIO2 reaching to the critical minimum increases and the period of the system increases accordingly.
so the effect of a on the system's behavior can be discussed from both rate constants and initial concentrations. All components match each other very well in the complex nonlinear system, once one of them out of a certain range, the whole behavior of the system will change tremendously. Occasionally the system will translate from one state to another. HIO2, a very important intermediate producing from R1 is also the reactant of R3. So k1ah2 is relative to the total producing rate of HIO2. The bigger value of k1ah2, the more HIO2 produces in R3. As the results, the time of the concentration of HIO2 reaching to the critical minimum increases and the period of the system increases accordingly.
In fact, the value of β is involved to the concentration of I– between R1 in which I– reacts with IO3– to form HIO2 and R5 that involves the hydrolysis of iodine to yield I–. Although with the decreasing β in the range of 10.00 to 0.015, the oscillating period of the system decreases obviously, the differential equations exists periodic solution. However, when β was in the range of 0.014 to 0.0001, chaotic behavior were observed in the BL oscillating chemical system as shown in Figure 1. So β = 0.015 is the bifurcation point of the BL system from periodic oscillation to chaotic behavior. It can be seen from Figure 5b, with the decreasing of β, the period of the system decreases obviously and the system becomes more and more instable and then reaches to chaos. That is to say, the behavior of the system translates from periodic oscillation to quasi–periodic oscillation. So it can be said that the system get to chaos through the way of quasi–periodic bifurcation.
The effect of γ on the BL nonlinear behavior
In order to appear oscillating phenomena, the value of y should be in the range of 4.0 x 10–6–4.0 x 10–3, further more the oscillation period decreases with the increasing of y in this range. When y is more than 4.0 x 10–2, the oscillating behavior disappeared after 20 min. However, the above differential equations doesn't exist periodic solution with γ ≤1.0 x 10 7. Due to  it can be divided into two parts,
it can be divided into two parts,  So the effect of γ on the system is consistent with that of α.
So the effect of γ on the system is consistent with that of α.
The effect of δ on the BL nonlinear behavior
When δ change in the larger range of 0.90–1.0 x 10–8, the differential equations exist periodic solution. That is to say, the system appears very stable oscillation behavior and the system's behavior changes slightly with the increasing of δ in this range. However, as δ reaches to 0.91, the characteristic of the system alters from periodic oscillation to chaos and chaotic behavior can be observed in the range of 0.91–500 within 20 min. So δ = 0.91 is the critical value of the system from periodic behavior to chaos. As mentioned above, the system's behavior does not change basically with S being in the wider range. Whereas the chaos appears unexpectedly as δ = 0.91. Therefore, another way for the system reaching to chaos is observed in the work. The more important thing is that the system becomes more and more regular after chaos with δ increasing in the range of 0.91–3.0(as shown in Figure 6) and this regular oscillation disappears gradually as δ increases continuously. That is to say, the behavior of the system translates from chaos to periodic oscillation. Figure 6e and 6f show the trajectories of the phase space before and after 20 min respectively. It is obviously that the former is chaos and the later is periodic oscillation. Moreover, the Largest Lyapunov exponent for the former is 0.7359, whereas for the later is only 0.2015. In fact, experimental results in references showed that complex dynamic behavior, including transition from simple periodic oscillations to complex mixed–mode oscillations and chaos were observed by varying different parameters in CSTR [23, 24]. The reason for appearing this complex phenomena in the nonlinear BL system is that although the whole system is far away from equilibrium, the relationship among each elementary reactions are weak and unstable factors are dominant and the behavior of the system is chaos. With the development of the system, these unstable factors becomes smaller and smaller, but some stable factors becomes stronger and dominant the whole system finally, so periodic oscillation is observed. On the other hand, when the nonlinear equations of system exhibit a chaotic phenomena, the inner fluctuations increase based on the exponent law by two times of the Largest Lyapunov exponent [25]. So the inner fluctuations will reach to a large value which can be seen, while one of the unstable trajectories of the strange attractor of system become more and more stable leading to periodic behavior appear. The transition mechanism from one nonlinear behavior to another likes which in life system. So it is helpful to understand the more complex behaviors of life system.
The effect of θ on the BL nonlinear behavior
Compared with the other variables and parameters, a little difference in the oscillation behavior was found when θ changes in the range of 8.0 x 10–4 to 8.0 x 104. The difference is that the period of the system increases slightly with increasing the θ value.
Conclusion
]]> According to the proposed chemical model involving four independent variables and seven irreversible steps, the theoretical calculation showed that the BL oscillating reaction could appear various dynamic behaviors such as regular periodic oscillation and chaos at different initial concentrations. The more important thing is the transition process of chaos to periodic oscillation state is observed in BL system for the first time. That is to say, the inverse Ruelle–Takens–Newhouse way is observed in BL system. The mechanism for appearing phenomena in the nonlinear BL system is very complex. Up to now, no relevant information on the kinetics of this process is available.
Mathematical calculation
Numerical integration for certain parameter values showed oscillations, but the model does not involve a true limited cycle. The 10 individual steps list below:

Based on the above chemical reactions, a model involving four independent variables and seven irreversible steps can be expressed as follows:
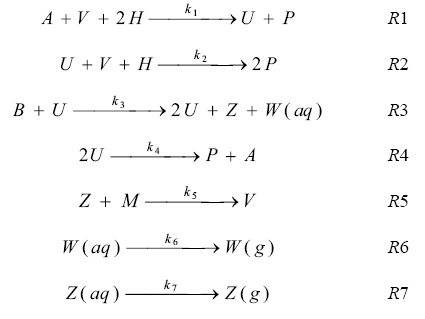

According to the above model the differential equations describing the dynamic behavior of the system are given below.


After the dimensionless transformation, the differential equations become as follows.

Double–precision computations are performed on a personal computer and the Mathematic 5.2 is used in all the simulations. The temporal concentrations of reaction system are calculated by Gear method. The simulation time is 50 minutes. The differential equations are resolved and the graphs of log u–t, log v–t, log z–t and log w–t are obtained.
Acknowledgments
This work was supported in part by the Project of International Cooperation between China and Ukraine (043–05), the National Natural Science Foundation (No. 20873101), the Natural Science Foundation of Gansu (1010RJZA015) and the project LKQN–08–9 of Northwest Normal University, China.
References
]]>1. Bray, W. C. J. Am. Chem. Soc. 1921, 43, 1262–1267. [ Links ]
2. Bray, W. C.; Liebhafsky. H. A. J. Am. Chem. Soc. 1931, 53, 38-44. [ Links ]
3. Edelson, D.; Noyes, R. M. J. Phys. Chem. 1979, 83, 212–220. [ Links ]
4. Sharma, K. R.; Noyes. R. M. J. Am. Chem.Soc. 1976, 98, 4345–4361. [ Links ]
5. Schmitz, G. Phys. Chem. Chem. Phys. 1999, 1, 4605–4608. [ Links ]
]]>6. Schmitz, G. Phys. Chem. Chem. Phys. 2001, 3, 4741–4746. [ Links ]
7. Melichercík, M.; Olexová, A.; Treindl, L. J. Mol. Catal. A: Chem. 1997, 127, 43–47. [ Links ]
8. Genigová, J.; Melichercík, M.; Olexová, A.; Treindl. L. J. Phys. Chem. A 1999, 103, 4690–4692. [ Links ]
9. Nardello, V.; Marko, J.; Vermeersch, G.; Aubry, J. M. Inorg. Chem. 1995, 34, 4950–4957. [ Links ]
10. Aubry, J. M.; Cazin. B. Inorg. Chem. A 1988, 27, 2013–2014. [ Links ]
]]>11. Kolar–Anic, Lj.; Misljenovic, D. M.; Stanisavljev, D. R.; Anic, S. R. J. Phys. Chem. 1990, 94, 8144–8146. [ Links ]
12. Valent, I.; Adamcíková, L.; Sevcík, P. J. Phys. Chem. 1998, 102, 7576–7579. [ Links ]
13. Láñová, B.; Vfesál, J. J. Phys. Chem. A 2002, 106, 1228–1232. [ Links ]
14. Schmitz, G.; Kolar–Anic, L. Z.; Anic, S. R.; Grozdic, T.; Vukojevic, V. J. Phys. Chem. A 2006, 110, 10361–10368. [ Links ]
15. Kéki, S.; Székely, G.; Beck. M. T. J. Phys. Chem. A 2003, 107, 73–75. [ Links ]
]]>16. Sevcík, P.; Adamcíková, L. Chem. Phys. Lett. 1997, 267, 307–312. [ Links ]
17. Sevcík, P.; Adamcíková, L. J. Phys. Chem. A 1998, 102, 1288–1291. [ Links ]
18. Stanisavljev, D. R.; Djordjevic, A. R.; Likar–Smiljanic, V. L. Chem. Phys. Lett. 2005, 412, 420–424. [ Links ]
19. Stanisavljev, D. R.; Djordjevic, A. R.; Likar–Smiljanic, V. L. Chem. Phys. Lett. 2006, 423, 59–62. [ Links ]
20. Sevcík, P.; Kissimonová, K.; Adamcíková, L. J. Phys. Chem. A 2000, 104, 3958–3963. [ Links ]
]]>21. Kissimonová, K.; Valent, I.; Adamcíková, L.; Sevcík, P. Chem. Phys. Lett. 2001, 341, 345–350. [ Links ]
22. Ren, J.; Gao, J. Z.; Yang, W. Portugaliae Electrochim. Acta. 2008, 26, 349–360. [ Links ]
23. Vukojevic, V.; Anic, S., Kolar–Anic, Lj. J. Phys. Chem. A 2000, 104, 10731–10739. [ Links ]
24. Ivanovic, A. Z.; Cupic, Z. D.; Jankovic, M. M.; Kolar–Anic, Lj.; Anic, S. R. Phys. Chem. Chem. Phys. 2008, 10, 5848–5858. [ Links ]
25. Xin, H. W. Nonlinear Chemistry. The University of Science and Technology Press. 1999. [ Links ]
]]>