
Comparison of models for the estimation of variance components for growth traits of registered limousin cattle
Comparación de modelos para la estimación de componentes de varianza de características de crecimiento de bovinos Limousin de registro
Ángel Ríos-Utrera1*, Vicente Eliezer Vega-Murillo2, Guillermo Martínez-Velázquez3, Moisés Montaño-Bermúdez4
1 Campo Experimental La Posta, INIFAP, km 22.5 carretera Veracruz-Córdoba, Paso del Toro, Medellín de Bravo, Veracruz, México, 94277, Tel. (285) 5960111, *Corresponding author. *e-mail: rios.angel@inifap.gob.mx.
]]> 2 Campo Experimental La Posta, LNLFAP, km 22.5 carretera Veracruz-Córdoba, Paso del Toro, Medellín de Bravo, Veracruz, México, 94277, Tel. (285) 5960111.3 Sitio Experimental El Verdineño, LNLFAP, km 17.5 carretera Navarrete-Sauta, Santiago Lxcuintla, Nayarit, México, 63570. Tel. (323) 2347800.
4 CENID Fisiología y Mejoramiento Animal, LNLFAP, km 1 carretera a Colón, Ajuchitlán, Querétaro, México. 76280. Tel. (419) 2920036.
Submitted December 20, 2010
Accepted February 02, 2011
Revised received February 15, 2011
Abstract
Six models to estimate genetic parameters for birth weight (BW), weaning weight adjusted to 205 days (W205), and yearling weight adjusted to 365 days (W365) were compared. Model A included direct genetic effects. Model AP allowed for direct genetic and permanent environmental effect of the dam. Model AM included direct genetic and maternal genetic effects. Models AMC and AMP were the same as Model AM but they also allowed for the covariance between direct and maternal genetic effects, and the common environmental effect due to the dam, respectively; and Model AMCP was fitted for all three random effects plus the covariance between direct and maternal effects. Models were compared using the likelihood ratio text. The AMC model was selected to be the most appropriate for BW and W205, whereas Model A was chosen for W365. When maternal effects were included, direct genetic variance and direct heritability estimates were reduced for BW and W205. Direct heritability estimates with appropriate models were: 0.13, 0.21 and 0.20 for BW, W205 and W365. Heritability of maternal effects with appropriate models was: 0.15 and 0.32 for BW and W205, and direct-maternal genetic correlations with appropriate models were: -0.67 and -0.69 for BW and W205, respectively.
]]> Key Words: Maternal Effects; Birth weight; Weaning weight; Animal Model; Limousin.
Resumen
Se compararon seis modelos para estimar parámetros genéticos para peso al nacimiento (PN), peso ajustado a 205 días (P205) y peso ajustado a 365 días (P365). El Modelo A incluyó el efecto genético directo (A); el Modelo AP incluyó, además del efecto genético directo, el efecto materno ambiental permanente (P); el Modelo AM incluyó el efecto genético materno (M), además de A; los Modelos AMC y AMP fueron iguales al Modelo AM, pero además incluyeron la covarianza entre A y M, y P, respectivamente; y el Modelo AMCP incluyó todos los efectos aleatorios, más la covarianza A-M. Los modelos fueron comparados utilizando la prueba de razón de verosimilitudes. El Modelo AMC fue el más apropiado para PN y P205, mientras que el A lo fue para P365. Cuando se incluyeron efectos maternos, los estimadores de la varianza genética y heredabilidad directas disminuyeron para PN y P205. Los estimadores de heredabilidad directa obtenidos con los modelos seleccionados fueron: 0.13, 0.21 y 0.20 para PN, P205 y P365. La heredabilidad materna obtenida con los modelos seleccionados fue: 0.15 y 0.32 para PN y P205, y la correlación genética entre A y M fue: -0.67 y -0.69 para PNy P205, respectivamente.
Palabras clave: Efectos maternos; Peso al nacer; Peso al destete; Modelo animal; Limousin.
INTRODUCTION
The magnitude of estimates of genetic parameters for growth traits of beef cattle may vary depending on breed group and genetic effects included in the statistical model, among other factors (Meyer, 1992; Ríos-Utrera, 2008). It has been reported that exclusion of maternal effects (maternal genetic and permanent environment) from the statistical model results in overestimation of variance and heritability of direct additive genetic effects for weight at weaning (Khombe et al, 1995; Robinson, 1996). Therefore, before performing the genetic evaluation of any economically important trait, selection of proper statistical model should be of primary interest for geneticists and producers, in order to formulate optimum breeding programs and to evaluate the genetic progress of ongoing programs.
For Simmental (Rosales-Alday et al., 2004), Charoláis (Ríos-Utrera et al., 2007) and Brahman registered cattle (Parra-Bracamonte et al., 2007) under Mexican production conditions, estimates of genetic parameters for growth traits have been reported. Limousin is a beef cattle breed from France; however, the Mexican Limousin originated from multiple importations of Limousin germplasm (semen and cows) from Canada and U.S.A. In the North American Limousin population, a positive genetic trend for several traits (e.g., weaning and yearling weight) has been found (NALF, 2011). In contrast, in spite of Limousin is one of the most important breeds (after Simmental and Charoláis) in beef production systems of Mexico, estimates of genetic parameters for this breed have not been reported. Knowledge of the size of the variances, as well as of the sign and size of the covariances, is necessary to improve beef productivity through selection of Mexican Limousin cattle.
The likelihood ratio test has been extensively used to compare the suitability of different statistical models for the estimation of genetic parameters of beef cattle. In a study carried out in Canada with crossbred bulls (Mwansa et al., 2000), the effect of including concomitant body weight and(or) a random dam effect in genetic evaluation models on variance components estimates for scrotal circumference was evaluated using likelihood ratio tests.
]]> Hoque et al. (2007) reported a comparison of different animal models with direct and including or excluding associated maternal effects for feed intake, feed-conversion ratio, residual feed intake and metabolic body weight in Japanese Black cattle using also such test. In Mexico, the likelihood ratio test has been applied to define proper statistical models for the national genetic evaluations of Salers and Brangus cattle (Domínguez-Viveros et al., 2009). Sometimes, however, it is difficult to make a good choice of the proper model (Swalve, 1993), while some other times researchers have failed to separate direct and maternal additive genetic effects for birth and other weights appropriately due to structure of data, complicating selection of appropriate model (Pelicioni et al., 2003). Based on the aforementioned, the aim of this study was to identify the most suitable model to estimate genetic parameters for weights at birth, weaning and yearling of Mexican registered Limousin cattle.
MATERIALS AND METHODS
Description of data
Field data for birth weight, weaning weight, and yearling weight, as well as pedigree information were supplied by the Mexican Limousin Breeders Association for the period from 1991 to 2006. All weaning and yearling weight records were adjusted to a 205- and 365-d basis, according to the Guidelines for Uniform Beef Improvement Programs (BIF, 2002). Adjusted weaning and yearling weights should be calculated for calves within an age range of 160 to 250 and of 320 to 410 days of age. Records on calves outside these ranges were eliminated from the analysis but not from the pedigree file. After basic edits, 8,910 animals with birth weight, 5,192 animals with weaning weight adjusted to 205 d, and 2,836 animals with yearling weight adjusted to 365 d records were used in the analysis. The number of sires with progeny in the data was 645, 488 and 315 for birth weight, weaning weight adjusted to 205 d and yearling weight adjusted to 365 d, respectively. The pedigree file, which incorporated all pedigree information available, was the same for these traits and consisted of 12,736 animals, including parents without records. Connectivity among different Limousin herds has been established to some extent through the use of common semen of Limousin sires from U.S.A., France and Mexico, and through auction of bulls and heifers among Mexican Limousin breeders. Numbers of records and sires for each trait and further details of the data structure are summarized in Table 1.

Definition of models
Each growth trait was analyzed with six different single trait animal models, like those described by Meyer (1992), to assess the importance of different maternal effects. The first model, Model A, was the basic animal model fitting the animal's direct genetic effect as the only random effect. Model AP included the direct genetic plus the common environmental effect due to the dam, fitted as an additional random effect. In contrast, Model AM attributed all the maternal effects to the genotype, fitting maternal additive genetic effects as a second random effect for each animal. Models AMC and AMP were the same as Model AM but they also allowed for a covariance between direct and maternal genetic effects, and a common environmental effect due to the dam (uncorrelated with the genotype of the dam), respectively. Finally, the most complete model, Model AMCP, was adjusted for all three random effects plus the covariance between direct and maternal genetic effects. All animal models included the same fixed effects, contemporary group and age of dam. Contemporary groups were constructed using herd, year, season, and sex of calf information, while dam age was taken into account by fitting it as a linear covariable.
]]> In matrix notation, the AMCP model was: y = Xβ + Z1a + Z2m + W1p + e, where y is the vector of records, β is a vector of fixed effects, a is an unknown vector of random direct additive genetic effects, a is an unknown vector of random maternal additive genetic effects, p is an unknown vector of random maternal permanent environmental effects, e is an unknown vector of random temporary environmental effects, and X, Z1, Z2, and W1 are known incidence matrices relating records to β, a, m, and p, respectively. The (co)variance matrix for random effects in the AMCP model was:
where A is the matrix of Wright's additive numerator relationships among all animals in the pedigree,  is the direct additive genetic variance,
is the direct additive genetic variance,  is the maternal additive genetic variance, σam is the direct-maternal genetic covariance, σ2pe is the maternal permanent environmental variance,
is the maternal additive genetic variance, σam is the direct-maternal genetic covariance, σ2pe is the maternal permanent environmental variance, 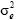 is the temporary environmental variance, and
is the temporary environmental variance, and  and IN are identity matrices with orders the number of dams and the number of observations, respectively.
and IN are identity matrices with orders the number of dams and the number of observations, respectively.
Estimates of genetic parameters
Variance and covariance components were estimated by Derivative-Free Restricted Maximum Likelihood, using the MTDFREML set of programs developed by Boldman et al. (1995). Convergence was assumed to have been reached if the variance of minus twice the logarithm of the likelihood (-2[log likelihood]) in the simplex was less than 10-8. After first convergence, restarts were performed to verify that it was not at a local minimum. Estimates of fraction of total phenotypic variance  due to maternal permanent environmental effects
due to maternal permanent environmental effects  , direct heritability
, direct heritability  , maternal heritability
, maternal heritability  and genetic correlation between direct and maternal additive genetic effects
and genetic correlation between direct and maternal additive genetic effects  were derived from estimates of variance and covariance components.
were derived from estimates of variance and covariance components.
Comparisons between models
Suitability of one model over another to fit significantly better birth, weaning and yearling weight data was determined via the likelihood ratio test (Dobson, 1990) for maternal permanent environmental effects, maternal genetic effects or covariance between direct and maternal genetic effects. Likelihood ratio tests were carried out subtracting the value of -2 [log likelihood] for the model with more parameters from that value corresponding to the model with fewer parameters. After that, the probability of rejecting the null hypothesis (e.g., maternal additive genetic variance is equal to zero) was calculated using the probchi function of SAS (SAS, 2001) with one degree of freedom (number of different parameters estimated for two models), since all comparisons were made for models that differed in only one random factor.
]]> RESULTS AND DISCUSSION
Estimates of (co)variance components and genetic parameters obtained with the six different animal models for birth weight, weaning weight adjusted to 205 days, and yearling weight adjusted to 365 days, together with values for -2 [log likelihood] are summarized in Table 2, while likelihood ratio test statistics for maternal permanent environmental effects, maternal additive genetic effects and direct-maternal genetic covariance for the same traits are in Table 3.
Birth weight
Estimates of direct additive genetic variance and direct heritability for birth weight were substantially reduced when maternal additive genetic effects and (or) maternal permanent environmental effects were added to the basic animal model. In particular, comparison of estimates of direct heritability for Model A and Model AM indicates that there was a decrease from 0.19 to 0.11 (Table 2). It seems that estimates of direct additive genetic variance included at least part of the maternal variance. Therefore, direct heritability estimates decreased when maternal effects were considered in the model. Including maternal additive genetic effects and(or) maternal permanent environmental effects gave similar estimates of direct heritability.
Likelihood ratio tests (Table 3) for maternal additive genetic variance (e.g., when comparing Model AM vs Model A) and direct-maternal genetic covariance (e.g., when contrasting Model AMC vs Model AM or Model AMCP vs Model AMP) indicates that maternal additive genetic effects and the covariance between direct and maternal additive genetic effects contributed to a better adjustment (P < 0.01) of birth weight data. Therefore, using estimates of genetic parameters from Models A and AM, would result in biased estimated breeding values. The maternal permanent environmental variance was only important (P < 0.01) when the permanent environment was fitted as the only maternal effect (Model AP) besides the residual. In addition, the value of -2 [log likelihood] for Model AMCP (24,503.9) was not considerably smaller (P>0.05) than the value of -2[log likelihood] for Model AMC (24,505.9). Therefore, Model AMC was considered the best animal model for birth weight. Estimates of direct and maternal heritability with the AMC animal model were similar.
For Simmental, Boran, Tropicarne, mixed breeds and crosses, and Salers cattle, Swalve (1993), Haile-Mariam and Kassa-Mersha (1995), Domínguez-Viveros et al. (2003), Demeke et al. (2003) and Domínguez-Viveros et al. (2009), assessing a comparable series of six different animal models (Models A, AP, AM, AMC, AMP and AMCP), concluded also that birth weight data were best described by an animal model including both direct and maternal genetic effects and the covariance between them, i.e., the AMC model was the most suitable animal model to analyze birth weight data. The estimates of direct heritability for birth weight (0.12 and 0.14) reported by Domínguez-Viveros et al. (2003) and Demeke et al. (2003) were similar to the current estimate reported here. However, estimates of direct heritability for birth weight by Swalve (1993) and Haile-Mariam and Kassa-Mersha (1995) were larger than corresponding estimate obtained in the present study with the AMC model (0.33 and 0.24 vs 0.13). On the other hand, current estimate of maternal heritability for birth weight was greater than corresponding estimates (0.15 vs 0.10, 0.07, 0.08 and 0.07) obtained by those authors with a model equivalent to Model AMC from our study. In contrast to the present result, Meyer (1992) for Angus, Hereford and Zebu crosses, Meyer (1993) for Polled Hereford, and Maiwashe et al. (2002) for Bonsmara cattle, concluded that the best animal model to fit their birth weight data included effects due to permanent environment of the dam along with direct and maternal additive genetic effects and their covariance, i.e., the best model was a model comparable to the AMCP model from our study. In a previous study (Meyer et al., 1993) conducted in Australia with Polled Hereford and Wokalup cattle, a model that included direct and maternal additive genetic effects, as well as permanent environmental effects of the dam, was chosen as the best animal model to fit birth weight data, contrasting also with our findings.
Weaning weight
As with estimates of direct additive genetic variance and direct heritability for birth weight, corresponding estimates for weaning weight were substantially inflated when ignoring maternal effects. Estimates of direct additive genetic variance for weaning weight ranged from 106 kg2 with Model AM to 209 kg2 with Model A, while estimates of direct heritability ranged from 0.17 to 0.33 with these two different animal models. In a previous study (Waldron et al., 1993) carried out in New Zealand with Angus and Hereford cattle, it was concluded that animal models which ignored maternal effects tended to overestimate direct heritability. In contrast, estimates of direct heritability were similar for each of the five different animal models including maternal effects (Table 2).
]]> Maternal additive genetic effects and the covariance between direct and maternal additive genetic effects contributed to a better adjustment (P < 0.01) of weaning weight data as indicated by likelihood ratio tests. Like the estimate of maternal additive genetic variance for birth weight, the estimate of maternal additive genetic variance for weaning weight remained practically constant after adding maternal permanent environmental effects to the AM model. The estimate of maternal additive genetic variance for Model AM was 96.6 kg2, and the corresponding estimate for Model AMP was 96.7 kg2. With Model AMCP, the value of -2[log likelihood] (31,855.6) did not substantially decrease compared to the corresponding value with Model AMC (31,856.1). Hence, Model AMC fitted weaning weight data better than any other animal model. When fitting the "best" animal model, estimates of maternal heritability were greater than estimates of direct heritability (0.32 vs 0.21), indicating that maternal additive genetic effects are more important than direct additive genetic effects for weaning weight in Mexican Limousin cattle.In agreement with present results, Spanish researchers (Gutierrez et al, 1997), working with Asturiana de los Valles cattle, found that a model fitting direct and maternal additive genetic effects and their covariance was the "best" animal model for weaning weight. For, Nelore, Boran, Bonsmara, Tabapua, Angus, Polled Hereford, Simmental and Limousin cattle, researchers from other countries (Ferraz Filho et al, 2004; Haile-Mariam and Kassa-Mersha, 1995; Maiwashe et al., 2002; Mercadante and Lôbo, 1997; Meyer, 1992; Meyer, 1993; Swalve, 1993; Van Niekerk and Neser, 2006) concluded that the most suitable model to analyze weaning weight data was a comprehensive model, equal to the AMCP model from our study. The estimate of direct heritability for weaning weight from the present study is within the range (0.16 to 0.35) of corresponding estimates reported for those eight breeds of cattle. Current estimate of maternal heritability, however, was greater than corresponding estimates (0.18, 0.14, 0.22, 0.06, 0.18, 0.12, 0.13, 0.10) for such breeds in those studies. In other previous studies (Ap Dewi et al, 1998; Demeke et al, 2003; Meyer et al, 1993), Models AMP, AM and AP were considered the best models to analyze weaning weight records. Estimates of direct heritability for weaning weight obtained with these three models were also low, in agreement with present estimate of direct heritability; however, the estimate of maternal heritability for weaning weight reported here is greater than corresponding estimates obtained in those previous studies with these three models.
Yearling weight
For yearling weight, fitting maternal permanent environmental effects or maternal additive genetic effects along with direct additive genetic effects in the model (Models AP and AM, respectively) did not significantly improved the -2[log likelihood], as indicated by likelihood ratio tests, i.e., estimates of maternal permanent environmental variance and maternal additive genetic variance were not different (P > 0.10) from zero. Therefore, the simplest animal model, Model A, was considered the most appropriate model for genetic evaluation of yearling weight records of Mexican Limousin cattle. Like estimates of heritability for birth and weaning weight, estimates of heritability for yearling weight were low, indicating that response to selection for these traits would be slow.
For Boran, Barca and Horro and their crosses with Holstein Friesian, Jersey and Simmental breeds of cattle in Ethiopia, Demeke et al. (2003) concluded also that an animal model that involved only the animal's direct additive genetic effect was a better fit for yearling weight data. However, the estimate of direct heritability for yearling weight reported by these authors was smaller than the corresponding estimate reported in the present study for Limousin cattle (0.13 vs 0.20). In preceding studies carried out in Australia (Robinson, 1996; Swalve, 1993), Brazil (Ferraz Filho et al, 2004; Mercadante and Lôbo, 1997) and Addis Ababa (Haile-Mariam and Kassa-Mersha, 1995), in which similar models to those used in the present study were compared, researchers concluded that maternal effects were important for yearling weight, and indicated that such effects should be considered in genetic evaluations of this trait. On the contrary, for Charoláis and Angus cattle in Germany, Grotheer et al. (1997) found that fitting maternal permanent environmental effects along with direct additive genetic effects in the model led to robust estimation of genetic variances for yearling weight, concluding that this form of the animal model is appropriate for the estimation of breeding values.
CONCLUSIONS AND IMPLICATIONS
In general, estimates of direct and maternal heritability obtained in the present study for weights of Mexican Limousin cattle at birth, weaning and yearling were low, suggesting that expected genetic progress by single trait selection would not to be high, mainly for birth weight. For birth weight and weaning weight adjusted to 205 d, the AMC model showed better adjustment for (co)variance components of registered Limousin data. When maternal effects were not included in the animal model, estimates of direct heritability were overestimated for birth and weaning weights, and consequently expected progeny differences will be biased, affecting selection efficiency. Maternal effects, genetic as well as permanent environmental, were not important for yearling weight, indicating absence of carry-over effects in Mexican Limousin cattle after weaning. Hence, a simple animal model, including only direct additive genetic effects of the animal as a random effect, besides the residual, is appropriate to analyze yearling weight data.
]]> REFERENCES
Ap Dewi, I., Ulutas, Z., Owen, J.B., Axford, R.F.E., Saatci, M. 1998. Genetic and commercial progress in a group breeding scheme for an upland suckler breed. In: Proceedings of the 6th World Congress on Genetics Applied to Livestock Production. Armidale, NSW, Australia, 11-16 January. 23: 169-172. [ Links ]
Boldman, K.G., Kriese, L.A., Van Vleck, L.D., Van Tassell, C.P., Kachman, S.D. 1995. A manual for use of MTDFREML. A set of programs to obtain estimates of variances and covariances (DRAFT). USDA, ARS, Washington, DC. 114 p. [ Links ]
Demeke, S., Neser, F.W.C., Schoeman, S.J. 2003. Variance components and genetic parameters for early growth traits in a mixed population of purebred Bos indicus and crossbred cattle. Livestock Production Science. 84: 11-21. [ Links ]
Dobson, A.J. 1990. An introduction to Generalized Linear Models. Chapman and Hall, New York. p. 57. [ Links ]
Domínguez-Viveros, I, Núñez-Domínguez, R., Ramirez-Valverde, R., Ruiz-Flores, A. 2003. Evaluación genética de variables de crecimiento en bovinos Tropicarne: I. Selección de modelos. Agrociencia. 37: 323-335. [ Links ]
Domínguez-Viveros, I, Rodríguez-Almeida, F.A., Ortega-Gutiérrez, J.A., Flores-Mariñelarena, A. 2009. Selección de modelos, parámetros genéticos y tendencias genéticas en las evaluaciones genéticas nacionales de bovinos Brangusy Salers. Agrociencia. 43: 107-117. [ Links ]
Ferraz Filho, P.B., Ramos, A. de A., da Silva, L.O.C., de Souza J.C., de Alencar M.M. 2004. Alternative animal models to estimate heritabilities and genetic correlations between direct and maternal effects of pre and post-weaning weights of Tabapua cattle. Archivos Latinoamericanos de Producción Animal. 12: 119-125. [ Links ]
Grotheer, V.V., Róhe, R., Kalm, E. 1997. Entwicklung einer zuchtwertschatzung für fleischrinder in Deutschland. 2. Mitteilung: Schatzung genetischer parameter. Züchtungskunde. 69: 349-365. [ Links ]
Gutiérrez, J.P., Canon, I, Goyache, F. 1997. Estimation of direct and maternal genetic parameters for preweaning traits in the Asturiana de los Valles beef cattle breed through animal and sire models. Journal of Animal Breeding and Genetics. 114: 261-266. [ Links ]
Haile-Mariam, M., Kassa-Mersha, H. 1995. Estimates of direct and maternal (co)variance components of growth traits in Boran cattle. Journal of Animal Breeding and Genetics. 112:43-52. [ Links ]
Hoque, M.A., Arthur, P.F., Hiramoto, K., Gilmour, A.R., Oikawa, T. 2007. Variance components due to direct genetic, maternal genetic and permanent environmental effect for growth and feed efficiency traits in young male Japanese Black cattle. Journal of Animal Breeding and Genetics. 124: 102-107. [ Links ]
Khombe, C.T., Hayes, J.F., Cue, R.I., Wade, K.M. 1995. Estimation of direct additive and maternal additive genetic effects for weaning weight in Mashona cattle of Zimbabwe using an individual animal model. Animal Science. 60: 41-48. [ Links ]
Maiwashe, A.N., Bradfield, M.J., Theron, H.E., van Wyk, J.B. 2002. Genetic parameter estimates for body measurements and growth traits in South African Bonsmara cattle. Livestock Production Science. 75: 293-300. [ Links ]
Mercadante, M.E.Z., Lobo, R.B. 1997. Estimativas de (co)variáncias e parámetros genéticos dos efeitos direto e materno de características de crescimento de fémeas de um rebanho Nelore. Revista Brasileira de Zootecnia. 26: 1124-1133. [ Links ]
Meyer, K. 1992. Variance components due to direct and maternal effects for growth traits of Australian beef cattle. Livestock Production Science. 31: 179-204. [ Links ]
Meyer, K. 1993. Covariance matrices for growth traits of Australian Polled Hereford cattle. Animal Production. 57: 37-45. [ Links ]
Meyer, K., Carrick, M.J., Donnelly, B.J.P. 1993. Genetic parameters for growth traits of Australian beef cattle from a multibreed selection experiment. Journal of Animal Science. 71:2614-2622. [ Links ]
Mwansa, P.B., Kemp, R.A., Crews, D.H., Kastelic, J.P., Bailey, D.R.C., Coulter, G.H. 2000. Comparison of models for genetic evaluation of scrotal circumference in crossbred bulls. Journal of Animal Science. 78: 275-282. [ Links ]
NALF. 2011. Spring 2011 statistics and trends. http://www.nalf.org/pdf/2010/dec22/1101_EPD.pdf. Consulted February 13, 2011. [ Links ]
Parra-Bracamonte, G.M., Martínez-González, J.C., Cienfuegos-Rivas, E.G., Garcia-Esquivel, F.J., Ortega-Rivas, E. 2007. Parámetros genéticos de variables de crecimiento de ganado Brahman de registro en México. Veterinaria México. 38: 217-229. [ Links ]
Pelicioni, L.C., de Queiroz, S.A., Albuquerque, L.G. 2003. Estimativas de parámetros genéticos para pesos ao nascer e mensais até 450 dias em bovinos Guzerá. Archivos Latinoamericanos de Producción Animal. 11: 34-39. [ Links ]
Ríos-Utrera, A. 2008. Estimadores de parámetros genéticos para características de crecimiento predestete de bovinos. Revisión. Técnica Pecuaria en México. 46: 37-67. [ Links ]
Ríos-Utrera, A., Martínez-Velazquez, G., Tsuruta, S., Bertrand, J.K., Vega-Murillo, V.E., Montaño-Bermúdez, M. 2007. Estimates of genetic parameters for growth traits of Mexican Charoláis cattle. Técnica Pecuaria en México. 45: 121-130. [ Links ]
Robinson, D.L. 1996. Estimation and interpretation of direct and maternal genetic parameters for weights of Australian Angus cattle. Livestock Production Science. 45:1-11. [ Links ]
Rosales-Alday, J., Elzo, M.A., Montaño-Bermúdez, M., Vega-Murillo, V.E. 2004. Parámetros y tendencias genéticas para características de crecimiento predestete en la población mexicana de Simmental. Técnica Pecuaria en México. 42: 171-180. [ Links ]
SAS. SAS/STAT User's Guide (Release 8.20). Cary, NC, USA. SAS Inst. Inc. 2001. [ Links ]
Swalve, H.H. 1993. Estimation of direct and maternal (co)variance components for growth traits in Australian Simmental beef cattle. Journal of Animal Breeding and Genetics. 110: 241-252. [ Links ]
Van Niekerk, M., Neser, F.W.C. 2006. Genetic parameters for growth traits in South African Limousin cattle. South African Journal of Animal Science. 36: 6-9. [ Links ]
Waldron, D.F., Morris, C.A., Baker, R.L., Johnson, D.L. 1993. Maternal effects for growth traits in beef cattle. Livestock Production Science. 34:57-70. [ Links ]
]]>