 , where S(t) and S(t–1) the current and previous values of the error derivative. Of course, this new value is only a crude approximation to the optimum value for the weight, but when applied iteratively this method is surprisingly effective.
, where S(t) and S(t–1) the current and previous values of the error derivative. Of course, this new value is only a crude approximation to the optimum value for the weight, but when applied iteratively this method is surprisingly effective.
Estimation of peak ground accelerations for Mexican subduction zone earthquakes using neural networks
Silvia R. García1, Miguel P. Romo1 and Juan M. Mayoral2
1 Instituto de Ingeniería, Universidad Nacional Autónoma de México, Del. Coyoacán 04510 Mexico, D. F., Mexico
2 Instituto de Ingeniería, Universidad Nacional Autónoma de México, Del. Coyoacán 04510 Mexico, D. F., Mexico Email: jmayoralv@ iingen.unam.mx
Received: May 23, 2006 ]]> Accepted: October 11, 2006
Resumen
Un análisis exhaustivo de la base de datos mexicana de sismos fuertes se llevó a cabo utilizando técnicas de cómputo aproximado, SC (soft computing). En particular, una red neuronal, NN, es utilizada para estimar ambos componentes ortogonales de la máxima aceleración horizontal del terreno, PGAh, y la vertical, PGAv, medidas en sitios en roca durante terremotos generados en la zona de subducción de la República Mexicana. El trabajo discute el desarrollo, entrenamiento, y prueba de este modelo neuronal. El fenómeno de atenuación fue caracterizado en términos de la magnitud, la distancia epicentral y la profundidad focal. Aproximaciones neuronales fueron utilizadas en lugar de técnicas de regresión tradicionales por su flexibilidad para tratar con incertidumbre y ruido en los datos. La NN sigue de cerca la respuesta medida exhibiendo capacidades predictivas mejores que las mostradas por muchas de las relaciones de atenuación establecidas para la zona de subducción mexicana. Para profundizar la evaluación de la NN, ésta fue también aplicada a sismos generados en las zonas de subducción de Japón y América del Norte, y para la base de datos usada en este artículo, los residuales de las predicciones de la NN y una regresión obtenida del mejor ajuste a los datos son comparados.
Palabras clave: Red neuronal, subducción, aceleración máxima, atenuación.
Abstract
An extensive analysis of the strong ground motion Mexican data base was conducted using Soft Computing (SC) techniques. A Neural Network NN is used to estimate both orthogonal components of the horizontal (PGAh) and vertical (PGAv) peak ground accelerations measured at rock sites during Mexican subduction zone earthquakes. The work discusses the development, training, and testing of this neural model. Attenuation phenomenon was characterized in terms of magnitude, epicentral distance and focal depth. Neural approximators were used instead of traditional regression techniques due to their flexibility to deal with uncertainty and noise. NN predictions follow closely measured responses exhibiting forecasting capabilities better than those of most established attenuation relations for the Mexican subduction zone. Assessment of the NN, was also applied to subduction zones in Japan and North America. For the database used in this paper the NN and the–better–fitted– regression approach residuals are compared.
Key words: Neuronal network, subduction, PGA's, attenuation.
]]> Introduction
Earthquake ground motions are affected by several factors including source, path, and local site response. These factors should be considered in engineering design practice using seismic hazard analyses that normally use attenuation relations derived from strong motion recordings to define the occurrence of an earthquake with a specific magnitude at a particular distance from the site. These relations are typically obtained from statistical regression of observed ground motion parameters.
Because of the uncertainties inherent in the variables describing the source (e.g. magnitude, epicentral distance, focal depth and fault rupture dimension), the difficulty to define broad categories to classify the site (e.g. rock or soil) and our lack of understanding regarding wave propagation processes and the ray path characteristics from source to site, commonly the predictions from attenuation regression analyses are inaccurate. As an effort to recognize these aspects, multiparametric attenuation relations have been proposed by several researchers (e.g. Youngs et al., 1997, Anderson 1997, Crouse 1991; Singh et al., 1989; Crouse et al., 1988; Singh et al., 1987; Sadigh, 1979). However, most of these authors have concluded that the governing parameters are still source, ray path, and site conditions.
In this paper an empirical neuronal network, NN, formulation that uses the minimal information about magnitude, epicentral distance, and focal depth for subduction–zone earthquakes is developed to predict the three components of peak ground acceleration, PGA's, at rock sites consisting of at most a few meters of stiff soil over weathered or sound rock. The NN model was obtained from existing information compiled in the Mexican strong motion database. Events with poorly defined magnitude or focal mechanism, as well as recordings for which site–source distances are inadequately constrained, or recordings for which problems were detected with one or more components were removed from the data. It uses earthquake moment magnitude, Mw, epicentral distance, ED, and focal depth, FD. The obtained results indicate that the proposed NN is able to capture the overall trend of the recorded PGA's. This approach seems to be a promising alternative to describe earthquake phenomena despite of the limited observations and qualitative knowledge of the recording stations geotechnical site conditions, which leads to a reasoning of a partially defined behavior. Although this paper is aimed at obtaining PGA's, similar techniques can be applied to estimate also spectral ordinates for any particular period.
Fundamental concepts regarding neural networks
Modeling of complex nonlinear systems using first principles is often quite cumbersome. In many cases the resulting model has to be simplified because handling large equations is not feasible or some phenomena (e.g. friction between rock blocks) are mathematically difficult to describe. As the input/output behavior of the system is of interest and the physical meaning of the model parameters is not well understood, universal approximators such as NN constitute a suitable alternative to overcome these problems.
NNs were originated in an attempt to build mathematical models of elementary processing units to represent biological neurons and the fl ow of signals among them. After a period of stagnation, with the discovery of efficient algorithms capable of fitting data sets, NN models have become more popular. Accordingly, NNs have increasingly been applied to build models that can approximate nonlinear functions of several variables and classify objects. A neural net is nothing more than a sophisticated black–box model that allows point to point mapping with nonlinear interpolation in between. Its domain is the approximation of systems, where the input space differs strongly from a linear description.
Mathematical description
]]> An Artificial Neural Network can be described by y(k)=f( (k),w), where y (k) is the output of the neural network,
(k),w), where y (k) is the output of the neural network,  (k) is the input vector and w is the vector containing the parameters (weights) wij that optimize the input–output mapping. A number of units (Figure 1) integrates a NN layer where the single inputs Ii are weighted and summed up (from 1 to the total number of inputs, Nj) to a resulting input via the net–function
(k) is the input vector and w is the vector containing the parameters (weights) wij that optimize the input–output mapping. A number of units (Figure 1) integrates a NN layer where the single inputs Ii are weighted and summed up (from 1 to the total number of inputs, Nj) to a resulting input via the net–function 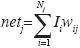 . The result is used to calculate the activation of the unit. In this investigation, the sigmoidal function
. The result is used to calculate the activation of the unit. In this investigation, the sigmoidal function  is chosen. Finally, a unit provides an output function to transform the activation into the output of the unit. A simple and often applied output function is the identity oj = aj.
is chosen. Finally, a unit provides an output function to transform the activation into the output of the unit. A simple and often applied output function is the identity oj = aj. A set of connected units forms a neural network with the capability of nonlinear input/output approximations. If the units are grouped into layers and all units of a layer are connected with the units of the subsequent layer a feedforward network is developed (i.e. static process) (Figure 2). This type of network propagates the input vector xi(k – 1) from the input–layer through one or more hidden layers to the output–layer, i.e. only in one direction. The dynamic process can be carried out by external feedback of delayed outputs and this is referred to as external recurrent networks.
If the number of units and the type of network connections are known, the weights of all units have to be adapted to the given process. This procedure is called identification or learning. Basically, in the identification procedure, the NN parameters have to be calculated such that the error between the measured and the predicted output is minimized. Quickprop (Fahlman, 1988) and the Cascade Correlation (Fahlman and Lebiere, 1991) learning algorithms provide suitable methods to calculate the weights more accurately. The results presented in this work were optimized using both methodologies. In order to make this paper self–contained, a brief description of them is presented below.
The quickprop algorithm, QP
The well known Backpropagation algorithm (Rumelhart, 1986), and subsequent–related works about calculating the partial first derivative of the overall error with respect to each weight can be improved through gradient descent optimization. If infinitesimal steps down the gradient are taken, reaching a local minimum is guaranteed, and it has been empirically determined that for many problems this local minimum will be a global minimum or at least a "good enough" solution for most purposes (Fahlman, 1988). This is the basis of the QP approximation.
Of course, if finding a solution in the shortest possible time is the objective, it is not recommended to take infinitesimal steps; it is desirable to select the largest steps possible without overshooting the solution. Unfortunately, a set of partial first derivatives collected at a single point tells very little about how large a step can be safely taken in weight space.
Fahlman (1988) developed a second–order method based loosely on Newton's method but in spirit more heuristic than formal. Everything proceeds as in standard backpropagation, but for each weight a copy of the error derivative computed during the previous training epoch (step) is kept, along with the difference between the current and previous values of this weight. The copied value for the current training epoch is also available at weight–update time. Then, two assumptions are made: i) the error versus weight curve for each weight can be approximated by a parabola the arms of which open upward; ii) the change in the slope of the error curve, indicated by each weight, is not affected by all the other weights that are changing at the same time. For each weight, independently, the previous and current error slopes and the weight–change between the points at which these slopes were measured to determine a parabola are used to find directly the minimum point of this parabola. The computation is very simple, and it uses only the local information to the weight being updated  , where S(t) and S(t–1) the current and previous values of the error derivative. Of course, this new value is only a crude approximation to the optimum value for the weight, but when applied iteratively this method is surprisingly effective.
, where S(t) and S(t–1) the current and previous values of the error derivative. Of course, this new value is only a crude approximation to the optimum value for the weight, but when applied iteratively this method is surprisingly effective.
The cascade correlation Algorithm, CC
]]> Cascade Correlation combines two key ideas: The first is the cascade architecture, in which hidden units are added to the network one at a time and remain unchanged thereafter.The second is the CC learning algorithm, which generates and installs the new hidden units. For each new hidden unit, the objective is to maximize the magnitude of the correlation between the new unit's output and the residual error signal that is being eliminated.
The cascade architecture is illustrated in Figure 3. It begins with some inputs and one or more output units, but with no hidden units. The number of inputs and outputs is dictated by the problem and by the Input/Output representation the experimenter has chosen. Every input is connected to every output unit by a connection with an adjustable weight. There is also a bias input, permanently set to +1. The output units may just produce a linear sum of their weighted inputs, or they may employ some non–linear activation function. In this investigation a sigmoidal activation function (output range from –1.0 to +1.0) has been used.
Hidden units are added to the network one by one. Each new hidden unit receives a connection from each of the network's original inputs and also from every pre–existing hidden unit. The hidden unit's input weights are frozen at the time the unit is added to the net; only the output connections are trained repeatedly. Each new unit therefore adds a new one–unit "layer" to the network, unless some of its incoming weights happen to be zero. This leads to the creation of very powerful high–order feature detectors; it also may lead to very deep networks and high fan–in to the hidden units.
As the learning algorithm begins with no hidden units, the direct input–output connections are trained as well as possible over the entire training set. To train the outputs weights (to back–propagate through hidden units) the QP algorithm, described earlier, is used. With no hidden units, QP acts essentially like the delta rule (interested readers could consult Pomerleau, D., 1987), except that it converges much faster. At some point, this training will approach an asymptote. When no significant error reduction has occurred after a certain number of training cycles controlled by a convergence parameter (mean square error is adopted in the proposed models), the network is run one last time over the entire training set to measure the error. If the network's performance is satisfactory, the training is stopped; if not, there must be some residual error that must be reduced further. Adding a new hidden unit to the network, using the unit–creation algorithm described, minor differences can be achieved. The new unit is added to the net, its input weights are frozen, and all the output weights are once again trained using QP. This cycle repeats until the error is acceptably small.
Data base
The database used in this study consists of 1058 records. These events were recorded at rock and rock–like sites during Mexican subduction earthquakes (Figure 4). Event dates range from 1964 to 1999. Events with poorly defined magnitude or focal mechanism, as well as recordings for which site–source distances are inadequately constrained, or recordings for which problems were detected with one or more components were removed from the data. To test the predicting capabilities of the neuronal model, 186 records were excluded from the data set used in the learning phase. One was the September 19, 1985, Mw=8.1 earthquake and the other 185 events were randomly selected, making sure that a broad spectrum of cases were included in the testing database.
The moment magnitude scale Mw is used to describe the earthquakes size, resulting in a uniform scale for all intensity ranges. If the user has another magnitude scale, the empirical relations proposed by Scordilis (2005) can be used.
In this paper the epicentral distance, ED, given in the database is considered to be the length from the point where fault–rupture starts to the recording site, as indicated in Figure 5. The third input parameter, FD, does not express mechanism classes; it is declared as a nominal variable which means that the NN identifies the event type through the FD crisp value. Some studies have led to consider that subduction–induced–earthquakes may be classified as interface events (FD < 50 km) and intraslab events (FD > 50 km) (Tichelaar and Ruff 1993, Youngs et al., 1997). This is a rough classification because crustal and interface earthquakes would be mixed (Atkinson and Boore, 2003), therefore it was considered that was not relevant for this work.
]]> The dynamic range of variables in the whole database is depicted in Figure 6. As can be seen, the interval of Mw goes from 3 to 8.1 approximately and the events were recorded at near (a few km) and far field stations (about 690 km). The depth of the zone of energy release ranged from very shallow to about 360 km.
Neural attenuation analysis
NN approximation
Modeling of the data base has been performed using the QP and the CC learning algorithms. Horizontal (mutually orthogonal PGAh1, N–S component, and PGAh2, E–W component) and vertical components (PGAv) are included as outputs for neural mapping. One first attempt was conducted using an average horizontal component PGAh1–h2 and PGAv as outputs (Figure 7). After trying many topologies, the best average–horizontal module yielded large differences for some cases between measured and evaluated ground accelerations, while the PGAv module behavior was quite acceptable using a simple alternative (QP, 2 layers/15 units or nodes each). In an attempt to improve the forecasting capabilities of the NN model, the individual horizontal PGA modules shown in Figure 8 were proposed.
Because of the failed attempt to find an efficient QP structure, the modules corresponding to PGAh1 and PGAh2 were developed using a CC structure, where nodes were added according to the relations discovered between the training patterns. The CC procedure is more time consuming than QP, but it guarantees an optimal topology. Using a 3.2 GHz processing speed computer it takes approximately 10 minutes and 2 hrs to run the QP and CC algorithms, respectively. The neural modules that met the convergence criterion (mean square error < 10%) have a total of 72 and 126 hidden nodes for PGAh1 and PGAh2, respectively. Details of the topology–selection process can be found in García et al. (2002).
NN results
The neuronal attenuation model for  was evaluated by performing testing analyses. The predictive capabilities of the NNs were verified by comparing the PGAs estimated to those induced by the 186 events excluded from the original database that was used to develop the NN architectures (training stage). In Figure 9 are compared the PGA's computed during the training and testing stages to the measured values. The relative correlation factors (R2≈0.99), obtained in the training phase, indicate that those topologies selected as optimal behave consistently within the full range of intensity, distances and focal depths depicted by the patterns. Once the networks converge to the selected stop criterion, learning is finished and each of these black–boxes become a nonlinear multidimensional functional. Every functional is then assessed (testing stage) by comparing their predictions to the unseen PGA (186) values of the database. As new conditions of Mw, ED, and FD are presented to the neural functional, R2 decreases, as shown in Figure 9 for the prediction of the excluded (unseen) data from the original dataset. This drop is more appreciable for the horizontal components. Nonetheless, as indicated by the upper and lower boundaries included in the fi gures on the right, forecasting of all three seismic components are reliable enough for practical applications.
was evaluated by performing testing analyses. The predictive capabilities of the NNs were verified by comparing the PGAs estimated to those induced by the 186 events excluded from the original database that was used to develop the NN architectures (training stage). In Figure 9 are compared the PGA's computed during the training and testing stages to the measured values. The relative correlation factors (R2≈0.99), obtained in the training phase, indicate that those topologies selected as optimal behave consistently within the full range of intensity, distances and focal depths depicted by the patterns. Once the networks converge to the selected stop criterion, learning is finished and each of these black–boxes become a nonlinear multidimensional functional. Every functional is then assessed (testing stage) by comparing their predictions to the unseen PGA (186) values of the database. As new conditions of Mw, ED, and FD are presented to the neural functional, R2 decreases, as shown in Figure 9 for the prediction of the excluded (unseen) data from the original dataset. This drop is more appreciable for the horizontal components. Nonetheless, as indicated by the upper and lower boundaries included in the fi gures on the right, forecasting of all three seismic components are reliable enough for practical applications.
]]> Neuronal Attenuation Parameters
A sensitivity study for the input variables was conducted for the three neuronal modules. Figure 10 shows the results from this revision. The results are strictly valid only for the data base utilized. Nevertheless, after several sensitivity analyses conducted changing the database composition, it was found that the following trend prevails; the Mw would be the most relevant parameter (presents larger relevance) then would follow the epicentral distance, ED, and the less infl uential parameter was the focal depth, FD. However, for near site events the epicentral distance could become as relevant as the magnitude, particularly, for the vertical component.
The selected functional forms incorporate the results of analyses into specific features of the data, such as the PGAh dependence of the geometrical ED–FD description. The NN for the horizontal components are complex topologies that provide almost the same weights to the three input variables. In the case of PGAv the functional offers superior attributes to Mw, describing PGAv as more dependent on Mw than on distances measures and focal depths. Through  mapping, this neuronal approach offers the flexibility to fit arbitrarily complex trends in magnitude and distance dependence and to recognize and select among the tradeoffs that are present in fitting the observed parameters within the range of magnitudes and distances present in data.
mapping, this neuronal approach offers the flexibility to fit arbitrarily complex trends in magnitude and distance dependence and to recognize and select among the tradeoffs that are present in fitting the observed parameters within the range of magnitudes and distances present in data.
Comparison of NN with traditional ground motion simulations
At this stage is convenient to note that traditionally the PGA's that are used to develop attenuation relationships are defined as randomly oriented (e.g. Crouse et al., 1988), mean (e.g. Campbell, 1988), and the larger value from the two horizontal components (e.g. Sabetta and Pugliese, 1987). Accordingly, considering the variety of PGA definitions used in most existing attenuation relations, it was deemed fairer to use the PGAh1–h2 prediction module shown in Figure 7 for comparison purposes. (It should be recalled that the PGAh1 and PGAh2 modules yield more reliable predictions than the PGAh1–h2 module.)
Figure 11 compares five fitted relationships to PGA data from interface earthquakes recorded on rock and rock–like sites. The two case histories correspond to a large and a medium size event are: 1) The September 19, 1985 Michoacán earthquake and 2) The July 4, 1994 event, respectively. Table 1 summarizes key information regarding these earthquakes. The estimated values obtained for these events using the relationships proposed by Gómez, Ordaz y Tena (2005), Youngs et al. (1997), Atkinson and Boore (2003) –proposed for rock sites– and Crouse et al. (1991) –proposed for stiff soil sites– and the predictions obtained with the PGAh1-h2 module are shown in Figure 11. It can be seen that the estimation obtained with Gómez, Ordaz y Tena (2005) seems to underestimate the response for the large magnitude event. However, for the lower magnitude event follows closely both the measured responses and NN predictions. Youngs et al. (1997) attenuation relationship follows closely the overall trend but tends to fall sharply for long epicentral distances. Although, as mentioned previously, the PGAh1–h2 module yielded important differences in the testing phase, its predictions follow closely the trends and yield a better behavior, in the full range of epicentral distances included in the data base, than traditional attenuation relations applied to the Mexican subduction zone. Furthermore, it should be stressed the fact that the September 18, 1985 earthquake was not included in the database used in the development of the neural networks and that this event falls well outside the range of values in such database, hence it is an example of the extrapolation capabilities of the networks developed in this paper. It is worth to note that while the NN trend follows the general behavior of the measure data, the traditional functional approaches have predefined extreme boundaries. Notice that for short distances the NN is closer to measured values than the traditional functional predictions, as indicated by Caleta de Campos station (Figure 11). On the other hand, when the intensity of the earthquake is moderate, most of the PGA's measured in rock sites are within a narrow band, thus generally the NN and traditional functionals follow similar patterns.
The generalization capabilities of the PGAh1–h2 module can be explored even more by simulating other subduction zones events. Measured random horizontal PGA's taken from Youngs et al. (1997) belonging to Japan and North America for two magnitude intervals (Mw: 7.8 – 8.2 and Mw: 5.8 –6.2) were compared to the NN predictions. These results are plotted in Figure 12. It can be seen that the NN prediction agrees well with the general trend even considering averages of both earthquake magnitude and focal depth.
As can be seen in Figures 11 to 12, the NN approach allows great flexibility with respect to the magnitude and distances dependencies, as it is demonstrated by the good agreement between estimations and data recordings in the total dynamic range tested. This neural network module can be extrapolated beyond the range of available data, and this proves that the model is capturing the physical attenuation mechanisms of the Mexican subduction zone and even the deep continental earthquakes not related to any specific geologic structure.
As a final testing of the potential advantages of NN over traditional regression procedures, the residuals of both methods (log residual = log of the observed value – log of the predicted value) for the same database are compared in Figure 13. The residuals for test patterns (horizontal component, HI) are presented as a function of magnitude Mw, distance ED and focal depth FD. The residuals were calculated for a multilinear regression equation obtained using a similar functional as the proposed by Crouse (Crouse et al., 1991), but the data base utilized in the training phase of the neuronal network. Crouse type functional was used because it yielded the best approximation for Mexican Subduction type events. The regression equation is presented below.
]]>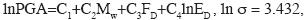

The standard deviation associated to the above functional is appreciably large; this is due to the significant scatter observed in the database used. The magnitude of the standard deviation can be reduced by eliminating further seemingly confl icting data. This was not done because the main purpose of the paper was to show the flexibility and forecasting capabilities of NN, not to develop an attenuation relationship based on traditional techniques. Therefore, the same database was used for both methods. As can be seen in Figure 13, the average residuals for the NN model are near to zero over all magnitudes, distances and depths tested. The standard deviation of the residuals for the NN model was 0.20, 0.23 and 0.28 for the vertical (PGAv) and the two horizontal components (PGAh1 and PGAh2) respectively.
Conclusions
This paper presents the application of two neural network models to estimate horizontal and vertical PGA at rock sites for Mexican Subduction Earthquakes. The neural models were developed from a set of known parameters (i.e. Mw, ED and FD). Comparisons shown that NN is capable of predicting the recorded values collected from the Mexican subduction zone. Furthermore, the experimental knowledge–based method is able to forecast the peak ground acceleration of events not even included in the database and registered in other world subduction zones. It is worthwhile to notice the powerful prediction capabilities of neural models developed in this paper. This work was aimed at developing neural network modules for practical applications that with a limited number of parameters would be able to describe the trends observed in measured peak ground accelerations. Ongoing research oriented to include both soil site conditions and seismogenic zone type using a neurofuzzy or neurogenetic systems is being conducted. This research is also oriented to obtain pseudo–spectral accelerations, PSA, and synthetic time histories.
Bibliography
AMBRASEYS, N. N. and R. SIGBJÖRNSSON, 2000. Reappraisal of the seismicity of Iceland. In: Polytechnica–Engineering Seismology. Earthquake Engineering Research Centre, University of Iceland. [ Links ]
ANDERSON, J. G., 1997. Nonparametric description of peak acceleration above a subduction thrust. Seismol. Res. Lett., (68) 1, 86–94. [ Links ]
ANDERSON, J. G. and Y. LEI, 1994. Nonparametric description of peak acceleration as function of magnitude, distance and site in Guerrero, Mexico. Bull. Seism. Soc. Am., 84, 1003–1017. [ Links ]
ATKINSON, G. M. and D. M. BOORE, 2003. Empirical ground–motion Relations for Subduction–Zone Earthquakes and Their Applications to Cascadia and other regions. Bull. Seism. Soc. Am., 93, 4, 1703–1729 [ Links ]
BRILLINGER, D. R. and H. K. PREISLER, 1985. Further analysis of the Joyner–Boore attenuation data. Bull. Seism. Soc. Amer., 75, 611–614 [ Links ]
CAMPBELL, K. W. 1988. Predicting strong ground motions in Utah, given in the paper Measurement, characterization, and prediction of strong ground motion by Joyner, W. B. and Boore D. M. In: Earthquake Engineering and Soil Dynamics II–Recent Advances in Ground–Motion Evaluation. 1988, 43–102. [ Links ]
CROUSE, C. B., Y. K. VYAS and B. A. SCHELL, 1988. Ground motions from subduction–zone earthquakes. Bull. Seism. Soc. Am.,78, 1–25. [ Links ]
CROUSE, C. B., 1991. Ground motion attenuation equations for earthquakes on the Cascadia subduction zone. Earth. Spectra, 7, 210–236. [ Links ]
FAHLMAN, S. E., 1988. Fast Learning Variations on Back–Propagation: An Empirical Study. Proceedings of the 1988 Connectionist Models Summer School, D. Touretzky, G. Hinton and T. Sejnowski, Ed. San Mateo, CA: Morgan Kaufmann, 38–51. [ Links ]
FAHLMAN, S. E. and C. LEBIERE, 1991. The cascade–correlation learning architecture, CUV–CS–90–100. School of Computer Science, Carnegie Mellon University, Pittsburgh, PA. [ Links ]
GARCÍA, S. R., M. P. ROMO, M. J. MENDOZA and V. M. TABOADA–URTUZUÁSTEGUI, 2002. Sand behavior modeling using static and dynamic artificial neural networks. Series de Investigación y Desarrollo del Instituto de Ingeniería SID/631, 32 p. [ Links ]
GOMÉZ, S. C., M. ORDAZ and C. TENA, 2005. Leyes de atenuación en desplazamiento y aceleración para el diseño sísmico de estructuras con aislamiento en la costa del Pacífico. Memorias del XV Congreso Nacional de Ingeniería Sísimica, México, Nov. A–II–02 [ Links ]
POMERLEAU, D., 1987. The meta–generalized delta rule: A new algorithm for learning in connectionist networks, tech. report CMU–CS–87–165, Robotics Institute, Carnegie Mellon University, September. [ Links ]
RUMELHART, D. E., G. E. HINTON and R. J. WILLIAMS, 1986. Learning internal representations by error propagation, Parallel Distributed Processing: Explorations in the Microstructure of Cognition, Rumelhart and McClelland, MIT Press, Cambridge, 1, 318–362. [ Links ]
SABETTA, F. and A. PUGLIESE, 1987. Attenuation of peak horizontal acceleration and velocity from Italian strong–motion records. Bull. Seis. Soc. Am. 77, 1491–1513. [ Links ]
SADIGH, K., 1979. Ground motion characteristics for earthquakes originating in subduction zones and in the western United States. Proc. Sixth Pan Amer. Conf., Lima, Peru. [ Links ]
SINGH, S. K., E. MENA, R. CASTRO and C. CARMONA, 1987. Empirical prediction of ground motion in Mexico City from coastal earthquakes. Bull. Seism. Soc. Am., 77, 1862–1867. [ Links ]
SINGH, S. K., M. ORDAZ, M. RODRÍGUEZ, R. QUAAS, V. MENA, M. OTTAVIANI, J. G. ANDERSON and D. ALMORA, 1989. Analysis of near–source strong motion recordings along the Mexican subduction zone. Bull. Seism. Soc. Am., 79, 1697–1717. [ Links ]
SCORDILIS, E. M., 2005. Empirical global relations for MS, mb, ML and moment magnitude. J. Seismology, (accepted for publication). [ Links ]
TICHELAAR, B.F., and L. J. RUFF, 1993. Depth of seismic coupling along subduction zones. J. Geophys. Res., 98, 2017–2037. [ Links ]
YOUNGS, R. R., S. M. DAY and J. P. STEVENS, 1988. Near field motions on rock for large subduction zone earthquakes. Earthquake Engineering and Soil Dynamics II – Recent Advances in Ground Motion Evaluation, ASCE, Geotechnical Special Publication, 20, 445–462. [ Links ]
YOUNGS, R. R., S. J. CHIOU, W. J. SILVA and J. R. HUMPHREY, 1997. Strong ground motion attenuation relationships for subduction zone earthquakes. Seismol. Res. Lett., (68) 1, 58–75. [ Links ] ]]>