Introducción
El apartado de análisis estadístico es básico en el protocolo de investigación, por lo que siempre debe estar presente. Este apartado se puede dividir en 2 grandes componentes: el análisis descriptivo y el análisis inferencial. Si bien el análisis estadístico sirve al investigador para la comprobación de sus hipótesis, debe ser utilizado de manera apropiada de acuerdo con los objetivos y el diseño del estudio.
El análisis descriptivo ya ha sido revisado en un artículo de esta misma serie1 y, como se comentó, forma parte de todos los protocolos de investigación. En contraste, el análisis inferencial solamente debe ser usado en los estudios donde se trata de comparar los resultados entre 2 o más grupos, o bien, se quiere establecer los cambios en un mismo grupo (después de una intervención terapéutica o evento).
Una inferencia es la elaboración de conclusiones a partir de las pruebas que se realizan con los datos obtenidos de una muestra de la población. Las pruebas estadísticas se emplean con la finalidad de establecer la probabilidad de que una conclusión obtenida a partir de una muestra sea aplicable a la población de la cual se obtuvo. Sin embargo, la elección de la prueba estadística apropiada representa un reto para los investigadores principiantes.
Existen diferentes pruebas estadísticas dentro del análisis inferencial, por lo que el objetivo de este artículo es de dar a conocer, de manera simplificada, la forma de seleccionar la prueba estadística acorde con los objetivos del estudio.
Bases para la elección de una prueba estadística
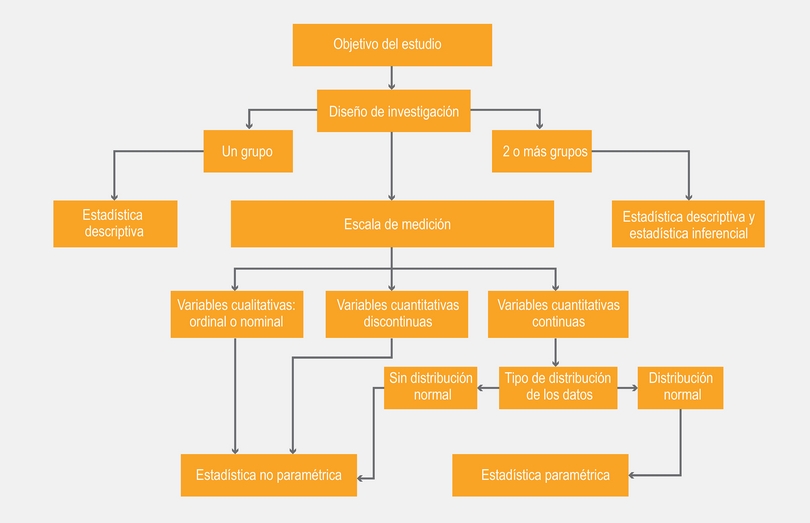
En la Figura 1 se establece una secuencia práctica para elegir la prueba estadística apropiada de acuerdo con cada protocolo de investigación. Los primeros 3 aspectos se describen a continuación.
Diseño de la investigación
El primer aspecto para la selección de una prueba estadística es el diseño de investigación. En el artículo de esta serie en el que se describen los diferentes diseños de investigación se comenta que cuando solamente existe un grupo y el objetivo de la investigación únicamente es especificar una o más características de dicha población, el tipo de estudio se denomina descriptivo, por lo que, como su nombre lo indica, solo es necesario emplear estadística descriptiva.2
Por su parte, los estudios comparativos se llevan a cabo con más de 2 grupos, como ejemplo podemos mencionar los que tratan de evaluar la utilidad de una intervención, como los ensayos clínicos controlados o aquellos en los que se buscan factores de riesgo (o estudios de causalidad), como el diseño de casos y controles.2
Se debe tomar en cuenta que en los estudios comparativos pueden existir 2 o más grupos. Existen protocolos que comparan 2 tratamientos diferentes; en otros se contrastan 3 o más dosis de un mismo fármaco; así, a los pacientes que se les da un tratamiento o una dosis determinada constituyen un grupo diferente o independiente.
Por otro lado, también es necesario identificar si en el estudio se trata de determinar los cambios de las variables de resultado, antes y después de una maniobra. Por ejemplo, si en una investigación se desea conocer la modificación de la saturación de oxígeno a un grupo de pacientes con crisis asmática después de administrar un broncodilatador, entonces, el valor previo al tratamiento es el valor basal de la saturación y la medición después de 15 minutos de administrado el broncodilatador constituirá el valor posterior. En este tipo de diseños, la comparación del valor antes y después se denomina dependiente o relacionada, lo cual indica que el cambio observado después del tratamiento depende del valor que el grupo tenía de manera basal.
Número de mediciones
El segundo aspecto por considerar en la selección de una prueba estadística es el número de mediciones de las variables de resultado. Los investigadores pueden analizar de diferentes formas los cambios de una variable a lo largo de un periodo. Por ejemplo, la respuesta al tratamiento con corticosteroides inhalados después de 4 meses en pacientes con asma se puede efectuar con un análisis del valor inicial previo al tratamiento y el valor final obtenido a los 4 meses, o bien, evaluar el cambio mensual durante los 4 meses. En el primer escenario se efectúa una medición antes y otra después; en el segundo escenario se llean a cabo 5 evaluaciones, incluida la basal, es decir, existen varias mediciones, las cuales se encuentran relacionadas.
Escala de medición de las variables
El tercer aspecto trascendente cuando se planea un análisis estadístico es la escala de medición de las variables, la cual ya ha sido explicada en otros 2 artículos de esta serie.1,3 En resumen, es necesario definir la naturaleza de cada uno de los datos o las mediciones que se realizan durante el desarrollo de una investigación; en general se pueden dividir en cualitativos o cuantitativos. A su vez, las variables cualitativas se clasifican en nominales y ordinales; las nominales agrupan las características similares entre sí en las que no hay diferencia entre una y otra, tales como el sexo (masculino/femenino) o el estado civil (soltero/casado/unión libre). Por su parte, las variables cualitativas ordinales ya tienen cierta dimensión, como el estadio o gravedad de una enfermedad (leve/moderada/grave).
Por su parte, las variables cuantitativas pueden ser de 2 tipos: cuantitativas continuas y cuantitativas discontinuas (también conocidas como finitas o de intervalo). Las cuantitativas continuas son 4: peso, longitud, volumen y tiempo (por ejemplo, kilogramos de peso corporal, estatura en centímetros, mililitros de orina y edad de una persona, respectivamente). Las discontinuas con variables numéricas que de alguna manera no se pueden dividir (número de hijos, número de embarazos, etcétera).
Estadística paramétrica y estadística no paramétrica
Siguiendo la secuencia de la Figura 1 se debe conocer que las diferentes pruebas estadísticas se dividen en 2 grandes conjuntos: las paramétricas y las no paramétricas. Una vez que se definió con claridad los 3 aspectos señalados se deberá establecer a cuál de estos 2 conjuntos pertenece la prueba. Tomando en cuenta la escala de medición de las variables, al conjunto de pruebas estadísticas paramétricas les corresponde las cuantitativas continuas; mientras que para las variables cualitativas (ya sean nominales u ordinales) y las cuantitativas discontinuas se incluyen las pruebas estadísticas no paramétricas.
Además, un requisito indispensable para seleccionar una prueba paramétrica es la distribución de los datos; en este sentido, solamente se debe utilizar este tipo de prueba cuando los datos muestran una distribución normal (es decir, semejante a una curva de Gauss). Se debe recordar que para determinar el tipo de distribución existen diferentes pruebas estadísticas, tales como Kolmogorov-Smirnov, Shapiro-Wilk o sesgo y curtosis.1,4
Como se observa en el Figura 1, de comprobarse que los datos no siguen una distribución normal, los investigadores deberán elegir una de las pruebas no paramétricas.
Elección de la prueba estadística
En el Cuadro 1 se resume la manera de selección de las pruebas estadísticas, tomando en cuenta el objetivo, número de grupos y la escala de medición de las variables. Como parte del análisis global de los datos nunca debe omitirse la inclusión del análisis descriptivo de los datos, es decir, es necesario que los investigadores resuman cada una de las variables estudiadas en medidas de tendencia central y de dispersión, tomando en cuenta la escala de medición de las variables y su distribución. De esta forma, las variables cualitativas habitualmente se presentan como frecuencia simples y proporciones (o porcentajes). El promedio como medida de tendencia central y la desviación estándar (o desviación típica) como medida de dispersión solo aplica con variables cuantitativas continuas y que tengan distribución normal; en variables cuantitativas discontinuas o continuas que no tienen dispersión normal se deben expresar como mediana y rango intercuartilar (también es correcto el valor mínimo y el valor máximo), respectivamente.1,4
Cuadro 1 Prueba estadística de acuerdo con los objetivos del estudio y la escala de medición de las variables
| Objetivos del estudio | Variables y distribución | Tipo de muestra | Prueba recomendada |
|---|---|---|---|
| Comparar 2 promedios | Cuantitativas, distribución normal | Muestras relacionadas Muestras independientes |
t de Student t de Student |
| Cuantitativas discontinuas y continuas sin distribución normal | Muestras
relacionadas Muestras independientes |
Wilcoxon U Mann Whitney |
|
| Comparar ≥ 3 grupos | Cuantitativas, distribución normal | Muestras relacionadas Muestras independientes |
Análisis de varianza (ANOVA) de 2 vías ANOVA de una vía |
| Cuantitativas discontinuas y continuas sin distribución normal | Muestras
relacionadas Muestras independientes |
Friedman Kruskal-Wallis |
|
| Comparar 2 grupos | Cualitativas nominales y ordinales | Muestras relacionadas Muestras independientes |
McNemar Chi-cuadrada* |
| Comparar ≥ 3 grupos | Cualitativas nominales y ordinales | Muestras
relacionadas Muestras independientes |
Q de Co
chran Chi cuadrada |
| Correlación de 2 variables | Cuantitativas, distribución normal | Muestras independientes | Coeficiente de correlación de Pearson |
| Cuantitativas discontinuas y continuas sin distribución normal | Muestras independientes | Coeficiente de correlación de Spearman |
*Utilizar prueba exacta de Fisher si algún grupo tiene valor < 5
Pruebas estadísticas paramétricas
Las pruebas disponibles para la comparación de grupos son numerosas; a continuación se comentan algunas de las más utilizadas.5,6,7 Si el investigador quiere comparar 2 grupos con variables cuantitativas continuas y con distribución normal, (dicho de otra forma, comparación de promedios entre 2 grupos), se puede elegir una prueba t (hay diferentes, la más conocida es la denominada t de Student). Tomando en cuenta lo descrito, esta prueba puede utilizarse en 2 escenarios diferentes:
Muestras relacionadas (un solo grupo antes y después).
Muestras independientes (comparación de 2 grupos).
A continuación un ejemplo: al evaluar el efecto de inmunoglobulina G sintética en un grupo de pacientes con hipogammaglobulinemia se mide la IgG posterior a la administración de la inmunoglobulina. Para hacer la comparación se toman los promedios del nivel sérico de IgG, primero administrando el compuesto en un grupo comparando contra la inmunoglobulina humana (grupo experimental versus grupo control). En el escenario 1, análisis de muestras relacionadas, se utiliza la prueba t para comparar la muestra basal de IgG (antes de la administración de la inmunoglobulina sintética) con la tomada 21 días después. Para el escenario 2, grupos independientes, se comparan los promedios de la IgG sérica en el grupo que recibe la inmunoglobulina sintética y el grupo que recibe inmunoglobulina humana.
Ahora bien, si lo que se desea es comparar más de 3 grupos (comparación de 3 o más promedios) se debe seleccionar una prueba denominada análisis de varianza o ANOVA. De esta última prueba se pueden distinguir al menos 2 variantes: ANOVA de una vía, cuando se comparan los promedios de 3 o más grupos independientes, y ANOVA de 2 vías, que se emplea cuando se pretende comparar los promedios de muestras relacionadas medidas 3 o más veces. Continuando con el ejemplo: los investigadores pueden ampliar el estudio de los niveles séricos de IgG, es decir, medición basal y a los 21 y 45 días después de la administración de la inmunoglobulina.
Pruebas estadísticas no paramétricas
Variables cuantitativas
Cuando la distribución de datos cuantitativos no sigue una distribución normal también hay diferentes pruebas estadísticas con las que se comparan las medianas. La prueba de Wilcoxon se utiliza para comparar un grupo antes y después, es decir, muestras relacionadas. Para la comparación de grupos independientes se debe emplear U de Mann-Withney.
En el caso de 3 o más grupos independientes se debe utilizar la prueba de Kruskal-Wallis (la cual es equivalente a ANOVA de una vía). La prueba Friedman es la que se recomienda cuando se comparan 3 o más muestras relacionadas (equivalente a ANOVA de 2 vías).
Variables cualitativas
Como se señala en el Cuadro 1 existen pruebas específicas para la comparación de grupos cuando la escala de medición de las variables es cualitativa. Retomando el mismo ejemplo, si tomamos solo a los pacientes que alcancen un nivel sérico de IgG > 400 mg/dL, en 2 grupos independientes se puede comparar el porcentaje de pacientes que alcanzan el nivel establecido de IgG utilizando la prueba de chi cuadrada, pero si las muestras son relacionadas deberá emplearse la prueba de McNemar. En caso de comparar 3 o más grupos independientes también se utiliza chi-cuadrada; en caso de muestras relacionadas, Q de Cochran.
Un punto a destacar cuando se emplean las pruebas de comparación de proporciones es que se deben cumplir ciertas condiciones: cuando el número de datos sea menor a 30 se aplicará la corrección de Yates, mientras que la prueba exacta de Fisher debe ser utilizada en lugar de χ2 cuando se comparan 2 grupos independientes si en algunas de las casillas de la tabla de contingencia se encuentra algún valor menor de 5.
Análisis de correlación
Cuando se desea establecer la relación de 2 variables cuantitativas continuas con distribución normal (por ejemplo, dosis de inmunoglobulina administrada con el nivel de IgG sérica) se utilizará el coeficiente de correlación de Pearson (r de Pearson). Sin embargo, cuando alguna de las 2 variables por correlacionar no siguen una distribución normal, la prueba que corresponde es el coeficiente de correlación de Spearman (rho de Spearman). Esta última es la que se aplica si se trata de analizar variables ordinales (ejemplo, el grado de desnutrición y su correlación con el grado de anemia).
Otras pruebas estadísticas
Si bien existen otras pruebas estadísticas, en este artículo hemos descrito las más utilizadas en los estudios de investigación médica publicados.8 Se recomienda la lectura de otras fuentes si los lectores desean conocer la forma de analizar estudios de causalidad para la identificación de factores de riesgo, con la estimación del riesgo relativo (RR) o razón de momios (OR).9 O bien, utilizar análisis multivariables como la regresión logística si en el protocolo de investigación se incluyen variables de confusión.10











 text new page (beta)
text new page (beta)