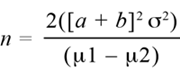Introducción

En toda investigación, clínica o básica, los datos obtenidos de las mediciones dan el sustento para realizar inferencias sobre la realidad. Además de la calidad de estas mediciones, el tamaño de la muestra, es decir, el número de sujetos de investigación a incluir en un estudio es uno los elementos más trascendentes. Así, cuando la evidencia disponible es limitada o escasa para apoyar una hipótesis, un estudio adicional con pocos sujetos sería insuficiente y no permitiría emitir conclusiones sólidas.¹ Por el contrario, aunque un exceso en el tamaño de la muestra facilita las inferencias, esto conlleva a un gasto injustificado en tiempo, dinero y esfuerzo.^1,2 Ambas situaciones tienen implicaciones éticas, dado que después del estudio con escasa muestra, la incertidumbre continuará al final de la investigación, y no habrá beneficio ni para los sujetos de investigación incluidos, ni para la población potencialmente susceptible. Tampoco es razonable (particularmente en estudios dónde se hará alguna intervención) someter a los participantes a riesgos, cuando con un número menor es posible lograr los objetivos de la investigación.^2,3

En general, para quienes están elaborando su protocolo de investigación, especialmente cuando se tiene poca experiencia, el cálculo del tamaño puede resultar una tarea complicada. El objetivo de este artículo es dar a conocer los aspectos más importantes para calcular de manera juiciosa, el número necesario de participantes en un estudio de investigación clínica, tomando como base a otros autores que han escrito extensamente sobre el tema.^1,4,5,6

Tamaño de la muestra en estudios clínicos

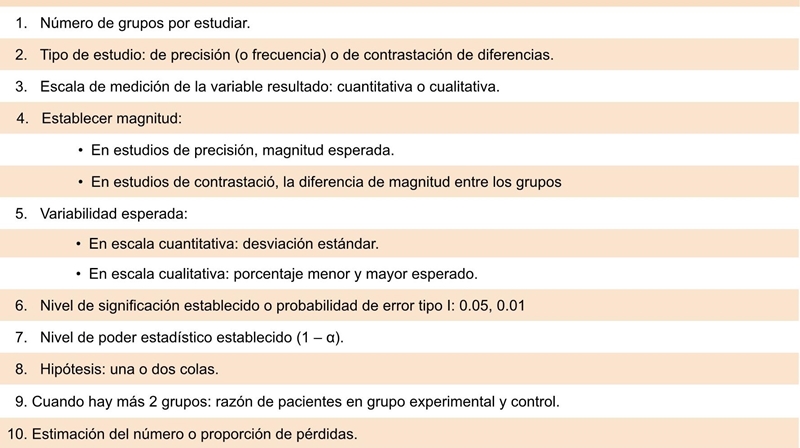
A continuación se describen los pasos iniciales para realizar el cálculo del tamaño de la muestra para un estudio clínico.^1,3,7 la información necesaria se encuentra sintetizada en el Cuadro 1. Con el propósito de hacerlo más práctico, en este artículo nos enfocaremos a tres tipos de investigación clínica de acuerdo con su propósito:⁸

Cuadro 1 Información necesaria para realizar el cálculo del tamaño de una muestra 

Enunciar el objetivo del estudio

Es fundamental recordar que una investigación es una propuesta sobre la dinámica de la naturaleza. Por ejemplo, el tratamiento A (nuevo broncodilatador) otorgado a pacientes con espasmo bronquial causa dilatación de su musculatura lisa y mejora el flujo de aire a través de la vía aérea. Este conocimiento surge con base a evidencias tanto biológicas, químicas, físicas y fisiológicas realizadas previamente, pero aún no confirmadas en humanos. Por ello, un investigador ejecutará un ensayo clínico para dar evidencia de la veracidad que el nuevo broncodilatador es eficaz en seres humanos. En ese momento surge la pregunta: ¿Cuántos pacientes se requieren para establecer que, con los datos obtenidos, la evidencia es suficiente para apoyar que el broncodilatador es eficaz? Aunque es imposible asegurar siempre un mismo comportamiento en cada ensayo (en este caso el resultado de la aplicación del broncodilatador), dado el número de posibles factores involucrados en un fenómeno, se puede estimar un margen estrecho de la probabilidad de que así suceda.^1,3 Este nivel de predicción es lo que nos permite hacer inferencias para futuros pacientes.

En una prueba diagnóstica, la pregunta de investigación pudiera ser ¿cuántos pacientes con neumopatía crónica necesito estudiar, para determinar la validez de la broncoscopia para establecer una causa infecciosa?; por su parte, para un estudio pronóstico, ¿cuántos pacientes con intolerancia a las proteínas de soya tengo que seguir para estimar la tasa de recuperación espontánea relacionada con la edad?

En estas tres interrogantes, el investigador debe tener una propuesta lógica y coherente con los conocimientos disponibles sobre la dinámica de la naturaleza, es decir, la formulación de los objetivos.⁹ Si no se disponen, entonces no es posible calcular el tamaño de la muestra para su estudio.

Estimar el efecto esperado y la variabilidad del mismo: estableciendo hipótesis

Una vez reconocido los objetivos del estudio es indispensable que el investigador elabore la o las respuestas o propuestas explicativas del fenómeno a estudiar, lo cual forma parte sustantiva del protocolo de investigación y se denomina hipótesis de trabajo.⁹

Tres aspectos son fundamentales para elaborar las hipótesis: el grado de cambio o la magnitud esperada del efecto, la escala de medición de las variables y la variabilidad del efecto. Las bases para determinar la magnitud esperada incluyen la información previa obtenida de estudios similares, así como lo que realmente sea útil en el ámbito clínico; en otras palabras, aunque un broncodilatador “incremente estadísticamente” el diámetro de los bronquiolos, no tendría utilidad clínica si los pacientes no perciben mejoría en su capacidad respiratoria. En este aspecto es conveniente mencionar que cambios notorios hablan de efectos fuertes y viceversa, por ello la regla es que entre más grande es el efecto esperado (magnitud), se requiere menor número de ensayos u observaciones (es decir, menor el tamaño de la muestra).

El segundo aspecto por considerar es que la medición de una variable puede ser evaluada con distintos instrumentos y, por tanto, generar datos en diferentes escalas de medición.¹⁰ Las escalas que usan medidas cuantitativas (por ejemplo, kilogramos, centímetros, litros), suelen permitir discriminar mejor los fenómenos que las escalas cualitativas (ejemplos: mejoría clínica en grados, o bien, muerte/ supervivencia).

Para poner en práctica ambos aspectos, primero regresamos al ejemplo del estudio de tratamiento para determinar la eficacia del broncodilatador para el broncoespasmo. Para lograr ese objetivo tenemos dos propuestas: en una se contrasta antes y después de utilizar el broncodilatador, la diferencia absoluta en milímetros del promedio del diámetro de la luz bronquial. La hipótesis es que el broncodilatador incrementará ≥ 50 % la luz bronquial (es decir, pasará de 0.2 a 0.3 mm). En la otra opción se comparan dos grupos: con y sin el broncodilatador y empleamos una variable de resultado en escala cualitativa, registrando la proporción o porcentaje de pacientes que incrementan ≥ 50 % el diámetro bronquial a partir del valor basal. La hipótesis describe que en 80 % de los pacientes que usan el nuevo broncodilatador se logrará este incremento, en comparación con 60 % del grupo de pacientes con el tratamiento habitual; así, la diferencia entre uno y otro grupo es de 20 %; esto último representa la magnitud esperada.

Si bien, ambos diseños son correctos, se debe tener en cuenta que las variables cualitativas tienen menor poder de discriminación por ser menos precisas en comparación con las mediciones cuantitativas. Por lo anterior, considerando la escala de medición existe otra regla en cuanto al cálculo del tamaño de la muestra: “las escalas con mayor poder de discriminación (cuantitativas versus cualitativas) siempre requerirán menor tamaño de la muestra y viceversa, a menor discriminación mayor tamaño de la muestra”.^1,3,7

Respecto al estudio de prueba diagnóstica, los autores apuestan a que la broncoscopia será útil si es capaz de confirmar un diagnóstico de infección (lo cual también se conoce como sensibilidad) en al menos 80 % de los pacientes con esta condición (magnitud esperada).

Mientras que para el estudio de pronóstico, los autores prevén que 75 % de los pacientes menores de 3 meses de edad con intolerancia a proteínas de la soya se recuperarán espontáneamente en un periodo 6 a 8 semanas, en comparación con 60 % que se recuperará en el mismo periodo, pero cuya edad de inicio de intolerancia es mayor a los 6 meses de edad. Entonces, la magnitud esperada de la edad como factor de buen pronóstico será de 15 %. Esto es lo mismo que asumir que a menor edad se incrementará al menos 2 veces (valor que también se conoce como riesgo relativo o hazard ratio) la probabilidad de un desenlace favorable, lo cual es otra manera de expresar la magnitud esperada.

El tercer aspecto cuando se elaboran las hipótesis es la variabilidad de la variable de desenlace, lo cual hace referencia a la diferencia observada en los resultados cada vez que se mide un fenómeno. Cuando un fenómeno es totalmente controlado y el factor de interés es el único involucrado en el resultado, basta con hacer un ensayo para demostrar su relación.

Lo anterior es la excepción; en la realidad los fenómenos en la naturaleza no pueden ser controlados totalmente, por ello se espera que en cada ensayo la respuesta (variable por medir) pueda cambiar en intensidad (cantidad) o en sentido (respuesta o no respuesta). Cuanto más precisas las respuestas, entonces la señal del fenómeno es más notoria. De esta forma se establece otra regla en el cálculo del tamaño de la muestra: “entre menos variabilidad de la variable de desenlace será menor el tamaño de muestra y viceversa, entre más variabilidad mayor será el número”.^1,5,6

Regresando a nuestros ejemplos, para calcular el tamaño de la muestra también es necesario establecer la variabilidad que pensamos encontrar. En el estudio de la eficacia de un broncodilatador, los investigadores identificaron dos estudios previos: en el primero, el diámetro interno bronquial fue en promedio de 0.2 mm con desviación estándar (DE) de 0.05 mm; mientras que en el segundo estudio, el promedio también fue de 0.2 mm pero la DE fue de 0.10 mm. En ambos, la DE representa la variabilidad, así que al elegir el resultado del primero para el cálculo del tamaño muestral, entonces el número de participantes será menor que si se eligiera el segundo estudio, ya que el primero mostró menor variabilidad.

Para el caso del estudio donde se evalúa la eficacia del nuevo broncodilatador cuando la variable de desenlace es con escala de medición cualitativa, y tomando como referencia estudios publicados, se considera que con el tratamiento habitual la eficacia tiene una variación de 10 % a partir del 60 % descrito previamente, es decir, la eficacia estimada irá de 50 a 70 %; la misma variación es esperada con el nuevo broncodilatador, o sea, de 70 a 90 %.

Para el estudio de la broncoscopia, el estimado deseado es de 80 %, pero los investigadores pudieran aceptar que esta sensibilidad cambie no más de 2 %, por lo tanto, la variación será de 4 %, es decir, de 78 a 82 %.

Especificar si se desea estimar la precisión de un efecto o diferencias entre grupos

Como parte de los elementos para el cálculo del tamaño de la muestra se requiere también tomar en cuenta el número de grupos por estudiar de acuerdo con el propósito del estudio.⁸ Como se describe en el Cuadro 1 existen dos opciones:

Los estudios de precisión por lo general son descriptivos para determinar el valor o la frecuencia (o bien, prevalencia o incidencia) de un dato, lo cual es aplicable también en los estudios de validación de una prueba de diagnóstico, lo cual ya fue mencionado en párrafos anteriores.^1,5,6

En estudios en los cuales se pretende contrastar los valores de la variable de resultado entre dos o más grupos, es mejor determinar el tamaño de la muestra bajo el concepto de pruebas de hipótesis estadísticas y buscar diferencias entre los grupos de estudio. Los enunciados se formulan con dos posibles respuestas: que los resultados entre los grupos de comparación en realidad son similares (hipótesis nula) o que son diferentes (hipótesis alterna); estas hipótesis tendrán significado y relevancia al momento de realizar el análisis estadístico e interpretar los resultados. En este sentido, al rechazar la hipótesis nula estaremos asumiendo que hay diferencia entre los grupos y, por lo tanto, aceptando la hipótesis alterna.

Como ejemplos para este tipo de cálculo del tamaño muestral aplican los estudios que hemos utilizado: para medir el efecto del broncodilatador y el de pronóstico de niños con intolerancia a la soya.

Errores tipos I y II

Cuando se realiza un cálculo del tamaño de la muestra existe la posibilidad de cometer 2 errores al momento de obtener e interpretar los resultados. Esto ocurre principalmente en los estudios donde se comparan dos o más grupos. El error tipo I consiste en rechazar la hipótesis nula cuando en realidad no hay diferencias entre los grupos analizados, lo cual, regresando a uno de nuestros ejemplos, implicaría que el nuevo broncodilatador es mejor que el control para aliviar el broncoespasmo. A la probabilidad de cometer este error se le conoce como alfa (α) o valor de p.

Por su parte, el error tipo II sucede cuando no se rechaza la hipótesis nula a pesar de que sí hay diferencia entre los grupos; a la probabilidad de cometer este error se conoce como beta (β). En el cálculo del tamaño de la muestra hay que considerar que el error alfa es más grave, por lo que la probabilidad de cometerlo debe ser baja; por consenso se ha delimitado que el nivel aceptable sea de 5 % o menor. Este valor en general es más conocido como p ≤ 0.05. Asimismo, es necesario tener en cuenta que entre más bajo se establezca este nivel será mejor (por ejemplo, 1 %, es decir, p ≤ 0.01). Sin embargo, hay que considerar que entre menor es el nivel, el tamaño de la muestra aumenta.¹

Respecto al error beta se acepta la posibilidad de cometerlo hasta en 20 %. Nuevamente, si se desea mayor seguridad en la decisión, esta probabilidad puede ser fijada en un valor menor (por ejemplo, 10 %). Si se decide esto, la implicación será que se incrementará el número de pacientes requeridos en el estudio. Ahora bien, el término poder o potencia se utiliza para la probabilidad de rechazar la hipó- tesis nula de una investigación con un determinado número de participantes incluidos en el estudio, dicho de otro modo: la probabilidad de que un estudio con un determinado tamaño de la muestra sea estadísticamente significativo cuando una diferencia realmente existe. Desde el punto de vista estadístico se expresa como:

De tal forma que si beta es igual a 20 %, entonces el poder es de 80 % o 0.80.

Una o dos colas

Otro elemento más que debe considerarse para calcular el tamaño de la muestra es la dirección de las hipótesis planteadas (Cuadro 1). No es suficiente que en las hipótesis se describa la magnitud, también se debe expresar hacia dónde se considera que se dirige el fenómeno. Para explicarlo tomaremos el ejemplo sobre la eficacia del nuevo broncodilatador: la descripción de la hipótesis que hemos utilizado indica que habrá mayor número de pacientes con incremento significativo del diámetro bronquial en comparación con el tratamiento habitual; sin embargo, los investigadores pudieran expresarlo en la siguiente forma: …el diámetro bronquial con el uso del broncodilatador será diferente en comparación con el otro grupo… De esta forma, en la primera hipótesis existe dirección, por lo tanto, el cálculo del tamaño de la muestra corresponde a “una cola”; mientras que para la segunda hipótesis no existe dirección, entonces el cálculo será a “dos colas”. La implicación de incluir la dirección en las hipótesis tendrá como consecuencia que un estudio a una cola requerirá menor tamaño de la muestra que un estudio a dos colas.

Pérdidas

Siempre es recomendable agregar 5 a 10 % del número de participantes al cálculo original del tamaño de la muestra, para asegurar la compensación de las pérdidas. Lo anterior es porque en cualquier estudio siempre existe una probabilidad de no participación de las personas o de abandono después de haberlos incluido en un estudio.

Ejecutando cálculos del tamaño de la muestra

Con el objetivo de poner en práctica esta lectura, a continuación, se describen los cálculos del tamaño de la muestra utilizando los ejemplos de los estudios descritos, tomando como referencia los datos de Cuadro 1. Para el cálculo con dichos datos se pueden utilizar programas libres en internet (http://www.sample-size.net/), aplicaciones (app) para equipos de telefonía móvil y tabletas (Medcal, EpiCal), o bien, tablas y nomogramas disponibles en libros de texto o artículos.¹¹ Asimismo, se pueden hacer los cálculos mediante fórmulas (algunas de las cuales se presentan en el apéndice de este artículo).

Otros aspectos por considerar