Introducción

Existen muchas investigaciones sobre el fenómeno de memoria en índices bursátiles, entre los cuales se encuentran el trabajo pionero de ^{Hurst (1951)}, el cual dio origen a modelos econométricos con memoria (corta o larga), o bien como el propuesto por ^{Granger y Joyeux (1980)} y ^{Hosking (1981)}, llamado modelo autorregresivo fraccionalmente integrado de medias móviles (ARFIMA o FARIMA), o el ^{Baillie et al. (1996)}, llamado modelo autorregresivo generalizado de heterocedasticidad condicional fraccionalmente integrado (FIGARCH), y todas sus variantes. Por otro lado, la manera de probar la existencia de memoria en una serie de tiempo ha ido cambiando, ya sea por la eliminación o introducción de nuevos argumentos o por la forma en que se estima el coeficiente de Hurst, lo cual conlleva a enfoques paramétricos, no paramétricos o semiparamétricos. Las pruebas más comunes son las propuestas por ^{Geweke y Porter-Hudak (GPH) (1983)}, ^{Higuchi (1988)} y ^{Robinson (1995)}, y algunas otras de tipo heurístico como el método del correlograma y el método de la varianza agregada (^{Taqqu et al., 1995}).

La importancia de probar la existencia de memoria, ya sea corta o larga, en una serie de tiempo, proviene de dos aspectos. Primero, hay que escoger el modelo adecuado que logre captar el fenómeno, ya que los modelos tradicionales basados en la hipótesis de mercado eficiente de ^{Malkiel y Fama 1970} (caminata aleatoria), en donde el dato relevante es el inmediato anterior, no permite retener en la memoria eventos muy remotos. En contraste, los modelos que captan la memoria suponen que toda la serie es importante, dado que el último dato de la serie de tiempo también impacta al primero en diferente proporción. En segundo lugar, hay que generar mejores pronósticos para la toma de decisiones, sean de carácter económico o financiero.

Los resultados de los trabajos que tratan de probar la existencia de memoria en índices bursátiles han sido marginales; por ejemplo, ^{Cheung y Lai (1995)} analizan dieciocho índices de mercado con frecuencia mensual en el periodo 1970-1992, y encuentran memoria larga en Austria, España, Italia y Japón. Estos autores destacan que hay que distinguir entre memoria en los rendimientos y memoria en la volatilidad. ^{Sadique y Silvapulle (2001)} analizan siete índices de mercado con frecuencia semanal entre 1993 y 1998. Estos autores encuentran memoria larga en Corea del Sur, Malasia, Singapur y Nueva Zelanda. Ellos también introducen la diferencia de estimar el coeficiente de Hurst en el dominio temporal y en el de frecuencias. ^{Henry Olan (2002)} analiza el índice de mercado con frecuencia mensual, en 1982-1998, de nueve países, y encuentra memoria larga en Corea del Sur. Este autor encuentra que existe poca evidencia de memoria larga en el resto de los índices, y que se debe más bien a burbujas especulativas y costos de transacción. ^{Hiremath y Kamaiah (2011)} analizan veinte índices de mercado con frecuencia mensual entre 1990 y 2000, y encuentran memoria larga en Brasil, Chile y Estados Unidos, haciendo diferencia entre mercados emergentes y consolidados. Otros trabajos que analizan índices y sus componentes son los de ^{Anoruo y Gil-Alana (2011)}, quienes analizan once índices de mercado de países africanos con datos de frecuencia diaria, con intervalos de estudio distintos en 1993-2006, y encuentran memoria larga en Egipto, Marruecos, Nigeria y Túnez. Asimismo, ^{Bhattacharya y Bhattacharya (2012)} estudian diez índices de mercado con frecuencia diaria en 2005-2011, y encuentran que Brasil, Chile, China, Corea del Sur, Hungría, India, Malasia, México, Rusia y Taiwán tienen memoria larga. Por otro lado, algunos estudios analizan índices y hacen hincapié en mercados en vías de desarrollo, como se muestra en el trabajo de ^{Barkoulas et al. (2000)}, donde se analiza el índice de Grecia en 1981-1990 con frecuencia mensual, hallando memoria larga en dicho índice. ^{Tolvi (2003)} estudia el índice de Helsinki Stock Exchange y veinte activos de empresas, con datos diarios de 1987-2001, y encuentra memoria larga en índices y en activos, destacando que es común la memoria larga en pequeños mercados. ^{Granger y Hyung (2004)} examinan el índice S&P500 con frecuencia diaria en 1928-2002. El análisis lo realizan por sub-periodos y encuentran fuerte evidencia de memoria larga en el índice, en términos absolutos; también encuentran que cuando existe rompimiento estructural en el modelo de estimación, no se distingue qué tipo de memoria tiene la serie. Por su lado, ^{Oh et al. (2006)}, analizan siete índices, dos de los cuales los examinan en frecuencia intradía (S&P500 y KOSDAQ). Estos autores normalizan los rendimientos por medio de la varianza, y encuentran que Alemania, Corea del Sur, Estados Unidos, Hong Kong, Francia, Japón y Reino Unido presentan eficiencia del mercado y que todas las series tienen memoria larga, con excepción de los dos índices analizados intradía. También muestran que los mercados emergentes presentan más volatilidad que los maduros. De igual forma, ^{Danilenko (2009)} examina el índice OMX Baltic durante 2000-2008. Este índice contiene a los sectores comunicaciones, energía, consumo, salud, financiero y tecnología, hallando memoria larga en dicho índice. ^{Mukherjee et al. (2011)}, estudia el índice Sensex, un aproximado del índice de la India, con frecuencia diaria de 1997-2009 en términos de rendimientos y niveles. Estos autores no encuentran memoria larga. ^{Saleem (2014)} analiza el índice de mercado y la eficiencia del mercado financiero de Rusia, y otros mercados como el petróleo, energía, bienes de consumo y telecomunicaciones, con frecuencia diaria, en 2004-2013, en forma de rendimientos, encontrando en los índices una alta correlación y memoria larga.

Este trabajo examina el fenómeno de memoria, ya sea corta o larga, de veinte índices de mercados de países en vías de desarrollo y desarrollados, con frecuencias diaria, semanal y mensual, para analizar si afecta el hecho de que un índice presente o no algún tipo de memoria debido a su periodicidad. En la segunda sección, se presenta de manera breve el concepto de memoria y su modelado; en la tercera, se mencionan las pruebas que detectan memoria; en la cuarta, se realiza un análisis estadístico de los índices de mercado y se aplican las pruebas de detección de memoria. Por último, se presentan las conclusiones.

1. Definición de memoria larga

Existen diversas definiciones de procesos estacionarios con memoria larga, cada una referida a un aspecto de la serie de tiempo, como puede ser la autocorrelación, varianza y densidad espectral. Los primeros que definieron un proceso estacionario con memoria larga fueron ^{Himpel y McLeod (1978)}, con base en el comportamiento de las autocovarianzas. Estos autores encontraron en su estudio que algunas series de tiempo tenían una caída lenta.¹ En esta investigación, se retoma la definición de memoria larga de ^{Beran (1994)}, la cual es como sigue: Si yt es un proceso estacionario, entonces existe un número real α0,1 una constante c>0 que satisfacen:

donde ρk son las autocorrelaciones de la serie yt. Otras definiciones alternativas se pueden encontrar en ^{Beran (1994)}, ^{Granger y Hyung (2004)} y ^{Palma (2007)}. Por ejemplo, vary-t≈cT-α cuando T→∞ y fω≈cω-β

cuando ω→0, donde fω es la densidad espectral y c es una constante positiva. En cada caso, α, β satisfacen 0<α<1 y 0<β<1. Como puede observarse, la primera definición se refiere a la varianza y la segunda a la densidad espectral.

Un modelo que puede capturar este tipo de fenómeno fue propuesto por ^{Granger y Joyeux (1980}) y ^{Hosking (1981)}. Por su parte, Hosking estableció una extensión del modelo ARIMA bajo la metodología Box-Jenkins (1976), en el que se propone que el modelo tuviera dos comportamientos. El primero trata con un modelo ARIMA 0,d,0 y el segundo con p≠0 y q≠0. El modelo ARFIMA o FARIMA p,d,q está representado por la siguiente ecuación:

donde yt es la variable de estudio, αL=1-α1L-⋯-αpLp, βL=1-β1L-⋯-βqLq y son los polinomios del operador rezago L, 1-Ld es el operador rezago fraccional² y εt es un proceso ruido blanco con media cero y varianza constante. El parámetro d es un número real que puede tomar valores en el intervalo cerrado -0.5,0.5. Si d<0.5, entonces yt es estacionaria y todas las raíces de ARp están fuera del círculo unitario. Si d>-0.5, entonces yt es invertible y todas las raíces MAq están fuera del círculo unitario. Si -0.5<d<0.5[xref ref-type="fn" rid="fn3" label="3"] ³, entonces yt es estacionaria e invertible, de tal manera que la función de autocorrelación ρk existe y es finita cuando k→∞ ( lim⁡k1-2dρk existe cuando k→∞).

El método para estimar el orden de integración ( d) de la serie yt se obtiene fuera del método propuesto por ^{Hosking (1981)}, ya que calcula por medio del rango reescalado ( R/s). Asimismo, ^{Sowell (1992)} obtiene el orden de integración ( d) dentro del proceso a través de la estimación exacta máxima verosímil en el dominio del tiempo, y supone que yt se distribuye normal con media y varianza constante ( y~Nμ,Ω), entonces, la función de verosimilitud está dada por:

donde Ω es la matriz de varianzas-covarianzas de y-μ y μ=Xβ, y es la media. Para obtener los parámetros del modelo se debe maximizar l con respecto al vector θd,α,β,σε2, como lo indican ^{Sowell (1992}), ^{Beran (1994)} y Doornik y Ooms (2003).

En el modelo clásico ARIMA p,d,q, el análisis de memoria larga se refiere al comportamiento de la correlación, varianza y densidad espectral. Mientras que en el modelo ARFIMA p,d,q, se presenta una caída exponencial de las correlaciones, y se observa también una caída lenta a la tasa k-α. La varianza tiene una caída igual a T-α y la densidad espectral tiene un polo que tiende a cero, igual a la tasa ω-β.

2. Pruebas de memoria larga

Existen diversos métodos para detectar memoria larga en una serie de tiempo yt, aunque el primer método fue propuesto por ^{Hurst (1951)}.⁴ El coeficiente de Hurst se obtiene por medio de la estimación de la siguiente ecuación a través del método de máxima verosimilitud:

donde RT/sT es la notación utilizada para el estadístico de rango reescalado RT es el rango ajustado, sT es la desviación estándar, c es la constante de proporcionalidad, T es el número de datos por intervalo y H es el coeficiente de Hurst.

El coeficiente de Hurst puede tomar valores en 0≤H≤1 , de tal manera que se pueden presentar los siguientes casos. Si 0<H<0.5 , la serie de tiempo yt presenta memoria corta, es antipersistente y los valores medios en el largo plazo regresan a su condicion inicial. Si 0.5<H<1.0 , la serie de tiempo yt  presenta memoria larga, es persistente y se espera que la media en el largo plazo nunca regrese a su condición inicial. Si H=0.5 , entonces es una caminata aleatoria, donde los eventos presentes no influyen en el futuro.

El coeficiente de hurst ( H ) se relaciona con el orden de integración ( d ) de una serie yt  , por medio de la siguiente ecuación: d=H-0.5 . Por otro lado, ^{Beran (1994)}, ^{Taqqu et al. (1995)}, y ^{Palma (2007)} realizan un resumen de los métodos más utilizados para detectar memoria larga, entre los cuales se pueden mencionar el correlograma, el gráfico de la varianza, la prueba de ^{Geweke y Porter-Hudak (1983)}, la prueba de ^{Higuchi (1988)} y el método de estimación semi-paramétrica de ^{Robinson (1995)} o el estimador local de Whittle.

Con el método del correlograma, derivado de la definición de memoria larga, se puede examinar la autocorrelación y a la autocorrelación parcial.⁵ Aunque este método es gráfico, también se puede obtener un orden de integración de la serie de tiempo, por medio de la estimación del valor de H , a través del método de máxima verosimilitud con la siguiente ecuación, para obtener la pendiente α1 :

la cual es utilizada para obtener el coeficiente de Hurst como H=α1/2+1 .

El método de la varianza agregada⁶ proviene de la definición de memoria larga en una serie y este se relaciona con el anterior método, ya que cuando se observa una caída lenta en la autocorrelación, se incrementa la varianza de la media de la muestra (^{Beran, 1994}). Si yt  es un proceso estacionario con memoria larga, entonces vary-t≈cT-α , donde c>0 y α=2H-2 . Para obtener el valor estimado de H , se estima la siguiente ecuación:

donde s2 es el valor de la varianza de cada corte y, x es el número de cortes. La pendiente de la regresión, la cual es negativa, es α1=2H-2 .

^{Higuchi (1988)} propuso un método para calcular la dimensión fractal d=2-H , que se describe como el índice de irregularidad de las serie de tiempo, pero supone que el total de observación se comporta de manera similar a una de sus partes. Considere

donde X es la variable de estudio, m , k y t son números enteros. El primero representa el inicio de la serie; el segundo, el corte de la serie y, por ende, el avance progresivo de la serie, y por último, t es el total de observaciones, de tal manera que satisfaga m≤k≤t .

Para obtener la dimensión fractal y, por ende, el coeficiente de Hurst, se realiza una estimación por medio del método de máxima verosimilitud de la ecuación (8).

donde Lmk representa el resultado obtenido en la expresión (7) y k el número de bloques realizados.

La prueba de ^{Geweke y Porter-Hudak (1983)} o GPH, también se conoce como método del periodograma. Considere la ecuación:

donde

es el periodograma, ωk=2πkT , son las frecuencias con su respectiva transformación con ωk=(-π,π) , β0 es la parte autónoma y β1 es la pendiente. La estimación de la ecuación (9) se realiza por el método de máxima verosimilitud, el cual proporciona el orden de integración -d=β1 e indirectamente el coeficiente de Hurst H=1-β1/2 de la serie yt .⁷

El estimador local de Whittle, propuesto por Robinson (1995), es un método semiparamétrico que se basa en el periodograma y que solo especifica la densidad espectral en su forma paramétrica cuando ω→0 . Es decir, se trata con frecuencias cercanas a cero.

La función discreta del estimador local de Whittle está dada por

donde m es un número entero menor a T/2 y satisface las siguientes condiciones: T→∞ , 1/m+m/T →0 y

es el periodograma. La frecuencia está dada por, ωk=2πkT con ωk=(-π,π) . En este caso, se remplaza G por su estimador, el cual se define como

y se obtiene finalmente,

La ventaja que presentan las pruebas de ^{Geweke y Porter-Hudak (1983)} y ^{Robinson (1995)}, es que adicionalmente se pueden hacer simulaciones con los valores que puede tomar el coeficiente de Hurst H , por medio de la variación del número de cortes representado por el parámetro α dentro de la regla m=Tα (con α=0.5 ).

3. Análisis empírico

El periodo de estudio considera de 1997.12 a 2014.2.⁸ Este trabajo analiza los principales índices del mercado accionario con diferente frecuencia: diaria, semanal y mensual. Los datos diarios solo coinciden en el inicio y el final, no así en cantidad, debido a días festivos o días donde hubo cierre de la bolsa por alta volatilidad. Los índices de mercado que se examinan, son: MERVAL-AR, ATX-AT, EURONEXT BEL-20-BE, IBOVESPA-BR, S&P/TSX Composite-CA, SMI-CH, SSE Composite Index-CN, DAX-DE, CAC 40-FR, FTSE 100-GB, HANG SENG Index-HM, Composite Index-ID, Nikkei 225-JP, KOSPI COMPOSITE Index-KR, IPC-MX, FTSE Bursa Malaysia KLCI-MY, STRAITS TIMES Index-SG, TSEC WEIGHTED Index-TW, NASDAQ Composite-US1 y S&P 500-US2.

La Gráfica 1 muestra los datos con frecuencia diaria, semanal y mensual, los cuales se presentan a escala logarítmica base 2, y en unidades de cientos. Se observan movimientos similares de todas las series y el rompimiento más importante se da en 2008, debido a la crisis de hipotecas en los Estados Unidos que contagia a todos los índices de manera instantánea. Aunque también se observan otros cambios como los de 1998 y 2001, los cuales coinciden con la crisis asiática y la crisis de la burbuja.com, pero no fueron tan fuertes y contagiosas como se observa en la de 2008. La debacle de 2008, sin duda, afectó los tipos de cambio y los rendimientos en los indicadores accionarios de muchas economías. Para incorporar el impacto de la crisis financiera de 2008 en los índices bursátiles bajo estudio, se requeriría analizar la influencia de muchas otras variables de tipo cualitativo y cuantitativo, por ejemplo: la regulación del mercado financiero en los Estados Unidos de América, los tipos de cambio, la tasa de interés de EUA, etc., lo que va más allá del alcance de esta investigación. Un análisis de la crisis económica de 2008, en el contexto de la presente investigación, se puede consultar en ^{Mian y Sufi (2008)} y ^{Machinea (2009)}.

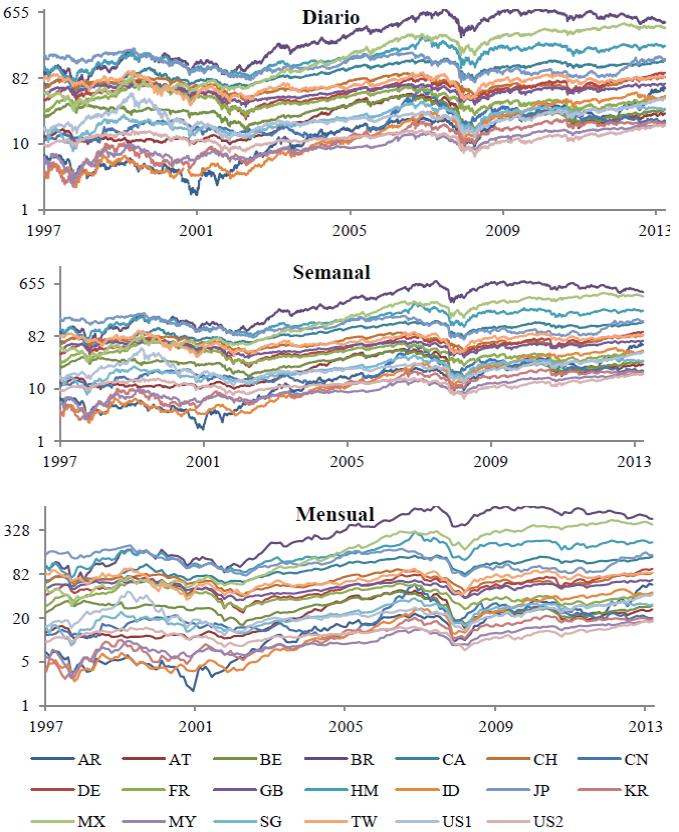
Nota: Elaboración propia con datos de finanzas yahoo.

Grafica 1 Índices del mercado accionario, diario, semanal y mensual  

Los días que, en promedio, las bolsas de valores del mundo podrían cotizar en un año son 261; de los cuales, los índices de mercado de países asiáticos y latinos son los países que menos días cotizan en promedio, ya sea que se tengan más días festivos o de alta volatilidad. En 1998, los índices de Argentina, Brasil, Hong Kong, Japón y Corea del Sur estuvieron cerradas al menos 15 días. En 2001, el índice de Yakarta estuvo 44 días cerrado, y el resto de índices como mínimo no cotizaron 10 días, con excepción del índice de China (el cual cotiza los 261 días al año, en promedio, hasta 2006). Los índices más estables en el año son el Dow Jones, S&P 500 y FTSE 100. En el periodo 2011- 2013 se observa que todos los índices de mercado empiezan a tener problemas similares a los observados en 2001, incluyendo China, que no cotizó 24 días en el año 2013.

El Cuadro 1 muestra los estadísticos de los diferentes índices de mercado con frecuencia diaria, los cuales fueron transformados a rendimientos logarítmicos, mostrando en general que los rendimientos son nulos. Los cambios en los rendimientos provienen de la volatilidad y estos normalmente son negativos, vistos por el sesgo; es decir, que solo los índices de Bélgica, Brasil, Hong Kong, Malaysia y México presentaron en este periodo más cotizaciones positivas que negativas. Por otro lado, se rechazó una distribución normal de los rendimientos en todos los índices, y todos se concentraron alrededor de la media, con puntos extremos, de ahí que la campana sea de tipo leptocúrtica y sesgada. Esto lo comprueba la prueba de Jarque-Bera, la cual rechaza la hipótesis de normalidad en todos los casos. La prueba aumentada de ^{Dickey-Fuller (1979)} muestra que —en todos los casos— ningún índice de mercado tiene una raíz unitaria, lo cual es indicio de estacionariedad, pero no de memoria larga. En este caso, y de acuerdo con ^{Lee y Schmidt (1996)}, la prueba KPSS puede mostrar indicios de este fenómeno, con una hipótesis nula de estacionariedad contra la de integración fraccional; para ello, se realizaron pruebas con constante, y constante y tendencia.

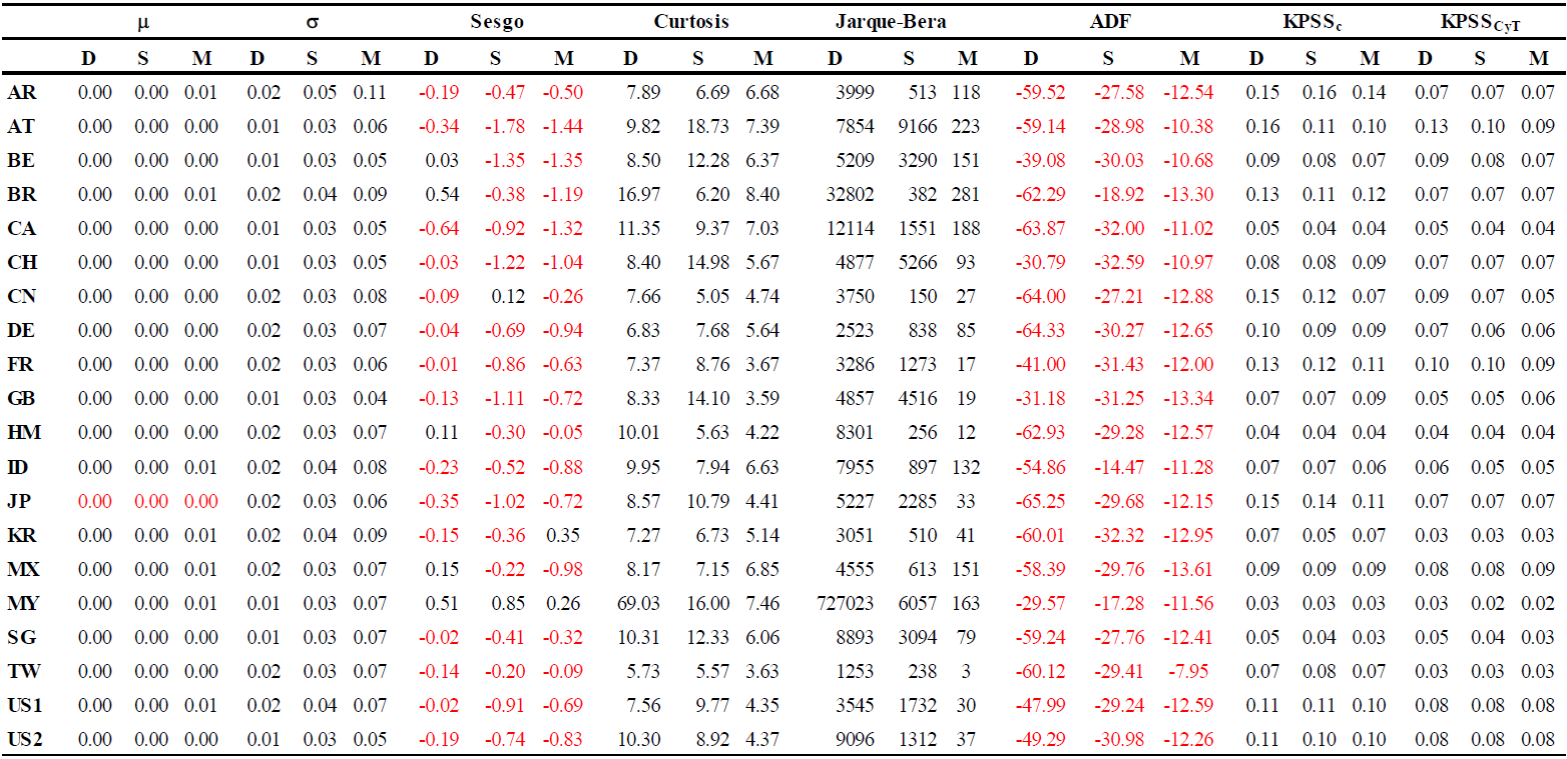
Nota: DS desviación estándar, J-B Jarque-Bera, ADF prueba aumentada de Dickey-Fuller, P es la probabilidad, KPSS es la prueba de ^{Kwiatkowski, Phillips, Schmidt y Shin (1992)}, D diario, S semanal y M mensual.

Cuadro 1 Estadísticos básicos de los índices del mercado accionario (diario) 

Por otro lado, también el Cuadro 1 muestra los estadísticos de los índices de mercado con frecuencia semanal, los cuales coinciden con la media a nivel diario, pero hay una disminución de la volatilidad en el sentido de que si sumamos la volatilidad diaria esta sería superior a la semanal; por eso, en general, solo hay un aumento alrededor de un 60%. En cuanto al sesgo y la curtosis, se muestra que el primero solo aparece en los índices de Malaysia y China, los cuales generaron rendimientos positivos para el periodo de estudio con cotizaciones de frecuencia semanal, y estos fueron marginales debido a que la mayoría se concentró alrededor de la media y a que en pocas ocasiones las cotizaciones fueron extremas, lo cual da origen a una distribución de tipo leptocúrtica, y comprobada por la prueba de distribución normal que en todos los casos son rechazados. El resto de los índices de mercado tienen un sesgo negativo. La prueba Dickey-Fuller aumentada rechaza la hipótesis nula de raíz unitaria; en consecuencia, el polinomio de raíces tiene invertibilidad y, por lo tanto, se está en presencia de series estacionarias. Por último, la prueba de estacionariedad KPSS en ambas versiones acepta la hipótesis nula de estacionariedad. Por lo tanto, al igual que el cuadro anterior, no existe memoria larga en las series de tiempo.

Finalmente, en el Cuadro 1, se observan los estadísticos de las series de tiempo con frecuencia mensual, en donde se observa que los rendimientos de Argentina, Brasil, Yakarta, Corea del Sur, México, Malaysia y el NASDAQ composite de Estados Unidos de América son diferentes de cero, en contraste con la periodicidad diaria y semanal. La volatilidad es estable si se compara con la diaria y semanal. El sesgo que presentan las series en su mayoría son negativas, con excepción de Corea del Sur y Malaysia, que tienen sesgo positivo, siendo este último índice el que en las tres frecuencia mostró un comportamiento positivo, lo cual quiere decir que, dentro del periodo de estudio, el índice de Malaysia en la mayoría de los casos tuvo rendimientos positivos por encima de la media. La distribución de los índices en su mayoría es del tipo leptocúrtico. Por lo tanto, la mayoría de los casos están cerca de la media con cotizaciones extremas, la excepción fue el índice de Francia y Taiwán, los cuales no rechazan normalidad. Esto se comprueba con la prueba de distribución normal Jarque-Bera, la cual dice que los rendimientos de Taiwán se distribuyeron normalmente, no así los de Francia. La prueba de estacionariedad KPSS acepta la hipótesis nula, por lo tanto, no todas las series muestran indicios de memoria larga.

En el Cuadro 1, se muestra que la mayoría de los índices son volátiles y que su distribución no es normal, ya que estos se concentran alrededor de la media con algunos puntos extremos, dando origen a colas pesadas, este hecho se debió a diferentes crisis financieras, como por ejemplo las del 2001 y 2008, ya que en ambos casos se tienen picos pronunciados, como se observa en la Gráfica 1.

En el Cuadro 2, se muestra el orden de integración estimado por los diferentes métodos mencionados en la sección 3, con el método del correlograma y rango reescalado. Todos los índices de mercado tienen memoria larga, la cual varía según la periodicidad. El método del correlograma se distingue de las demás estimaciones, porque el orden de integración en la serie es mayor cuando se toma la frecuencia diaria, y menor cuando es mensual. En contraste con el método del rango reescalado, el orden de integración superior se presenta con datos semanales; las otras dos frecuencias son similares.

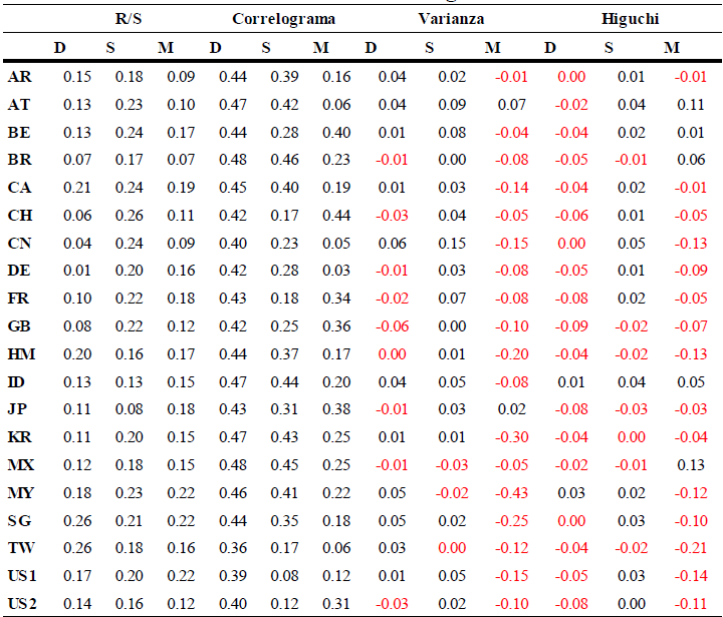
Nota: D-diario, S-semanal, M-mensual, d-orden de integración d=H-1⁄2.

Cuadro 2 Estimación del orden de integración d 

Con el método de la varianza, se observan varios hechos relevantes. Por ejemplo, con frecuencia mensual, las series se comportan con reversión a la media, es decir, ruido rosa; y con frecuencia diaria, los resultados son mixtos; en el caso semanal, es ruido negro en su mayoría. El método de Higuchi arroja resultados un tanto similares al anterior método, aunque —en este caso— las frecuencias mensual y diaria presentan comportamientos semejantes; el orden de integración en los índices sugeriría que —en el largo plazo— estos regresan a sus rendimientos medios. En el Cuadro 2, también se observan varios resultados. Primero, el orden de integración de los índices de mercado cambia cuando varía la frecuencia. Segundo, esta variación depende del método que se utilice para su estimación; por ejemplo, la Gráfica 2 muestra los cuatro métodos utilizados para la obtención del orden de integración, se observa que con el método de rango reescalado y del correlograma, todos los índices tienen memoria larga.

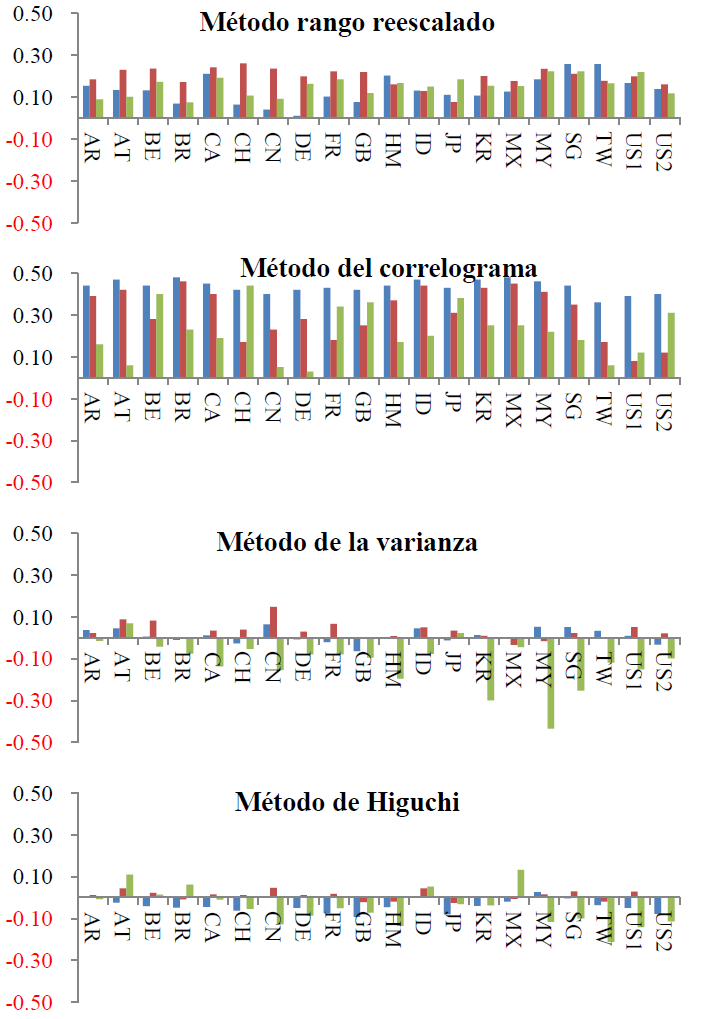
Nota: frecuencia, azul-diario, rojo-semanal y verde-mensual.

Gráfica 2 Orden de integración de acuerdo con el método utilizado 

Con el método de la varianza y rango reescalado, los resultados son mixtos; es decir, con frecuencia mensual se obtiene un orden de integración negativo de los índices de mercado, lo cual indica memoria corta o de reversión a la media, significativa.

En el Cuadro 3, se muestra la prueba de Geweke y Porter-Hudak para las frecuencias diaria, semanal y mensual. En primer lugar, la prueba se realizó utilizando diferentes cantidades de datos con T0.45 , T0.50 y T0.55 , donde T es el número de datos; para analizar si el orden de integración varía cuando se cambia la cantidad de datos utilizados en su obtención. El Cuadro 5 muestra las estimaciones del orden de integración de cada uno de los índices de mercado, de los cuales solo los de Austria, Bélgica, Canadá, China, Corea del Sur, Indonesia, Malaysia, Singapur y Taiwán son estadísticamente diferentes de cero. De estos nueve índices de mercado, el orden de integración cambia de signo de positivo a negativo dentro de la misma frecuencia, lo cual es signo de volatilidad variante en los bloques que se utilizaron para la obtención del orden de integración. Por ejemplo, en Indonesia cambia de -0.07 a 0.16, Corea del Sur de -0.09 a 0.08, Malaysia de -0.08 a 0.07 y Singapur de -0.2 a 0.09, con frecuencia diaria. Por otro lado, en los índices también se observa que el orden de integración, aunque no cambia de signo, varía demasiado. Por ejemplo, el índice de mercado de Canadá con frecuencia diaria cambia de 0.01 a 0.12; es decir, primero se comporta como una caminata aleatoria y después como una serie que posee memoria larga. Por último, el orden de integración varía de acuerdo con la periodicidad de que se trate; Taiwán con frecuencia diaria tiene indicios de memoria larga, y con mensual, como índice de memoria corta.

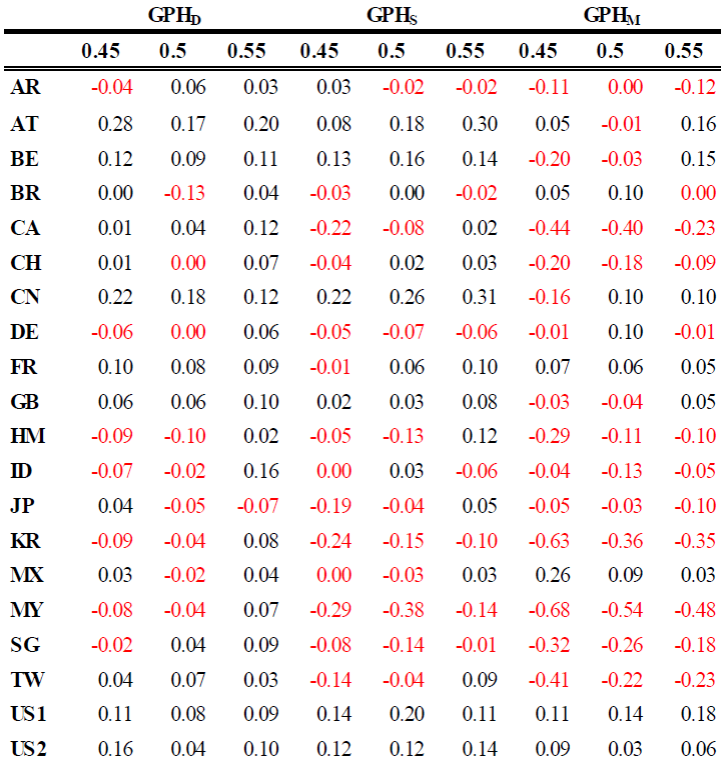
Nota: Elaboración propia con software Gretl, donde GPH_D Diario, GPH_S Semanal y GPH_M Mensual.

Cuadro 3 Prueba de Geweke y Porter-Hudak, Diario, Semanal y Mensual 

En el Cuadro 4, se muestran los resultados obtenidos de aplicar la prueba del estimador local Whittle propuesto por ^{Robinson (1995)}, los cuales son similares a los obtenidos con la prueba de Geweke y Porter-Hudak, ya que en los mismos índices de mercado, los cambios de signo de positivo a negativo y la variabilidad del orden de integración son parecidos.

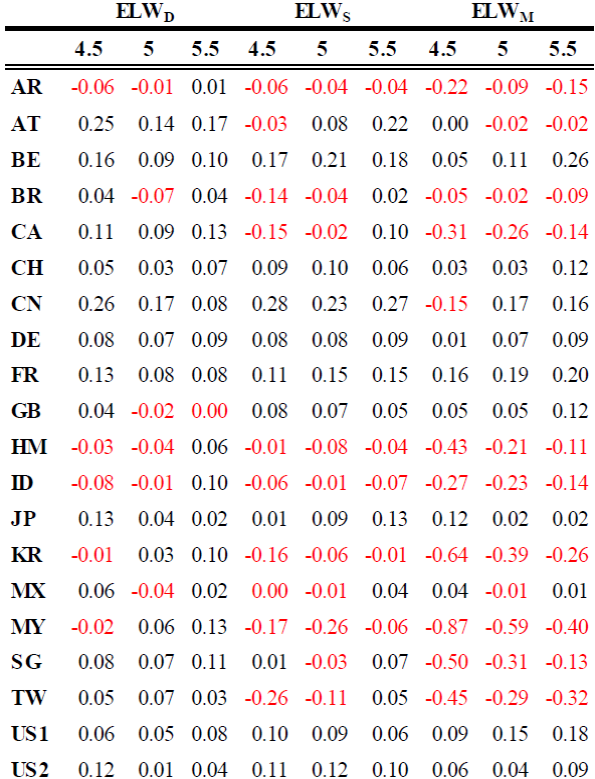
Nota: Elaboración propia con software Gretl, donde ELW_D Diario, ELW_S Semanal y ELW_M Mensual,

Cuadro 4 Estimador local de Whittle, Diario, Semanal y Mensual 

Los resultados obtenidos en los Cuadros 3 y 4 muestran que cada índice tiene un comportamiento diferente en cada periodicidad, aunque el intervalo de estudio no varía. Teniendo en cuenta este hecho, cada índice de mercado tiene que ser analizado y pronosticado. Por ejemplo, los inversionistas todos los días ven movimientos erráticos de varios índices de mercado, dado que no todos ellos invierten al mismo tiempo sino por etapas, los movimientos observados se desvanecen regresando a sus rendimientos medios mensuales.

El Cuadro 5 muestra los resultados de la estimación del modelo ARFIMA para cada uno de los índices de mercado que presentaron algún grado de memoria. Por medio del método propuesto por ^{Sowell (1992)}, se realizó la estimación exacta con el método de máxima verosimilitud. Primero, con periodicidad diaria, se observa que todos los índices presentan memoria larga, aunque es marginal; solo China, Singapur y Yakarta presentan considerable memoria larga. Por otro lado, se muestra la prueba ARCH, la cual tiene un valor alrededor de 2; por lo observado, la hipótesis nula debería ser rechazada. De esta manera, los resultados no son consistentes dado la relación no lineal de la varianza condicional y la variable independiente.

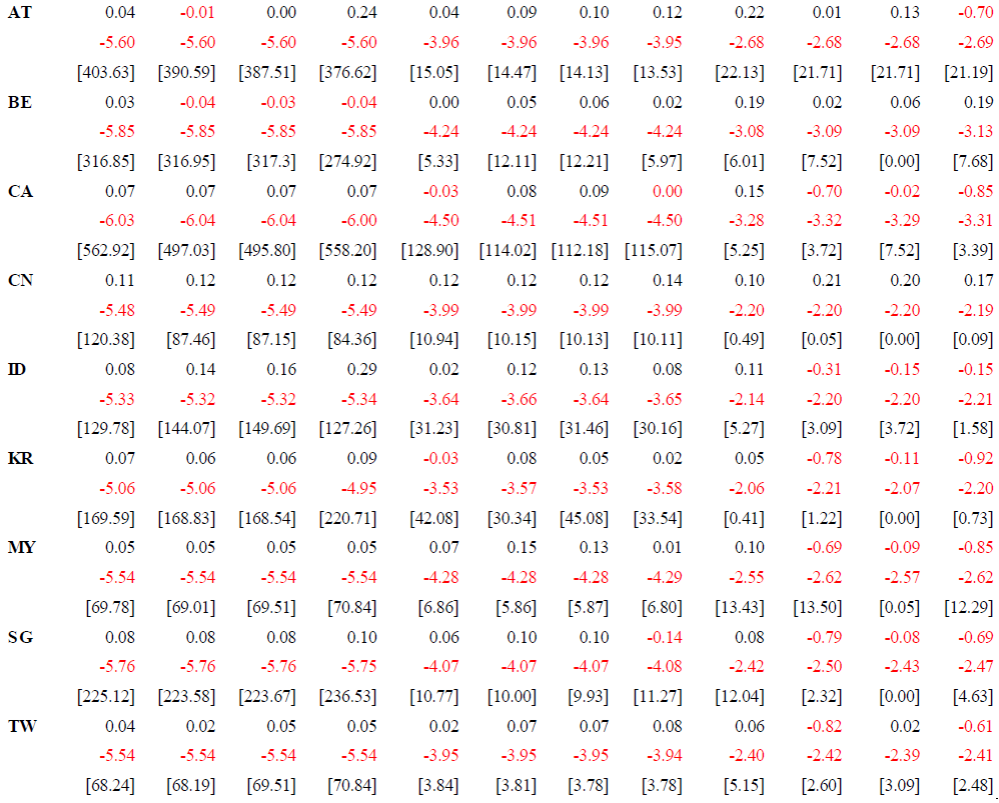
Nota: Elaboración propia con software Matrixer, entre corchetes se encuentra la prueba ARCH con rezago de primer orden.

Cuadro 5 Estimación del modelo ARFIMA 

Por otro lado, el Cuadro 5 muestra también, según se puede observar, las estimaciones para los índices de mercado con frecuencia semanal, que arrojan resultados similares, es decir, presentan memoria larga los índices de los países de Austria, China, Singapur y Yakarta; pero, también presentan indicios de ARCH, al menos de primer orden, aunque esto disminuye considerablemente al transcurrir el tiempo. Finalmente, también en el Cuadro 5, se muestran los resultados obtenidos de la estimación del parámetro de integración ( d ), junto con la prueba ARCH de primer orden, con periodicidad mensual, y de acuerdo con los resultados obtenidos, el índice de mercado de China es el único que presenta memoria larga sin problemas de ARCH, al igual que Corea del sur, aunque en su caso es memoria corta. En los demás índices, se observa una clara influencia por los problemas de ARCH, lo que genera variaciones que van de un memoria corta a larga, y viceversa. En este contexto, se esperaría que las cotizaciones del índice bursátil de China tuvieran cambios bruscos a la alza y a la baja, sin regreso al rendimiento medio y viceversa; mientras que para el índice bursátil de Corea del Sur, se esperaran cambios y, en un periodo largo, regresaría a su rendimiento medio.

Después de haber realizado el análisis estadístico y las pruebas de memoria, el índice de China y Corea del Sur, son los únicos que presentan el fenómeno de memoria. En el primer caso, se tiene memoria larga, y en el segundo, corta. El resto de los índices están influenciados por la volatilidad, típicas de series de corte financiero y, por lo tanto, la mejor forma de estimarlos es por medio el modelo GARCH, propuesto por ^{Bollerslev (1986)}.

3. Conclusiones

En este trabajo, se aplicaron diferentes métodos para estimar el orden de integración de una serie de tiempo, partiendo del método seminal del rango reescalado y concluyendo con uno de los más recientes, el estimador local de Whittle, propuesto por ^{Robinson (1995)}. Se observó que el orden de integración varía de acuerdo con el método que se utilice. Por ejemplo, con el método de rango reescalado y correlograma, todos los índices bursátiles tienen memoria larga, mientras que con el método de la varianza y Higuchi, los resultados son mixtos; es decir, pueden tener memoria corta con datos mensuales, y memoria larga con datos diarios, y viceversa. Con los métodos de Geweke y Porte-Hudak y el estimador local de Whittle, varios de los órdenes de integración de los diferentes índices de mercado no pasaron la prueba de significancia estadística, dejando solo a los índices de Austria, Bélgica, Canadá, China, Corea del Sur, Indonesia, Malaysia, Singapur y Taiwán, como candidatos a poseer algún tipo de memoria. Al analizar estos índices de mercado, se llegó a la conclusión de que varios de ellos eran sensibles a la información que los genera, observado un cambio de signo de positivo a negativo. Por otro lado, el orden de integración cambia cuando se modifica la periodicidad, sin modificar el intervalo de estudio, lo cual es indicio de que la estimación del orden de integración se ve contaminada por la volatilidad que presentan los índices diariamente, o porque los diferentes métodos de estimación del orden de integración no discriminan el fenómeno de la volatilidad. Por último, el índice de mercado de China presenta memoria larga con un orden de integración de 0.20 y un criterio de Akaike de -2.20, mientras que el índice de mercado de Corea del Sur es un proceso con reversión a la media, con un orden de integración de -0.11 y un criterio de Akaike de -2.07, ambos con frecuencia mensual. El principal mensaje de esta investigación es que debe tomarse en cuenta, para estudios futuros, que la periodicidad de una serie de tiempo cualquiera es relevante en el resultado, en virtud de los resultados mixtos que aquí se presentan.

Por último, es importante mencionar que en un proyecto futuro de investigación se realizará un análisis comparativo de diversas técnicas, con fundamentos financieros, distinguiendo sobre memoria larga y equilibrio de largo plazo; la tarea será monumental por el número de países estudiados; alrededor de 20.