INTRODUCCIÓN
En este artículo nos proponemos compartir algunas reflexiones en torno a ciertos debates surgidos en las primeras clases de un Seminario de geometría donde se abordan conocimientos geométricos, didácticos y aquellos otros que abonan a un análisis de las prácticas de enseñanza desplegadas por los y las docentes-estudiantes3 participantes del curso. En este Seminario se incluye el uso de un programa de geometría dinámica (GeoGebra), recurso novedoso para muchos de los y las cursantes, que promueve ciertas tensiones entre los conocimientos geométricos disponibles, producto de su experiencia de trabajo con lápiz, papel e instrumentos de geometría, y los que demanda el uso del software. Dicho seminario es el tercero de la Licenciatura en Enseñanza de la Matemática para la Educación Primaria, carrera que se brinda en la Universidad Pedagógica Nacional-Argentina (UNIPE). En consecuencia, cuando inician esta asignatura, los y las docentes-estudiantes han tenido una experiencia vinculada a la problematización de algunos objetos de enseñanza que intervienen activamente en la producción de conocimientos, a partir de preguntas que intencionalmente se proponen en la formación para promover el análisis de sus propias prácticas.
En el trayecto formativo mencionado, asumimos que las construcciones geométricas ofrecen la posibilidad de poner en juego las propias conceptualizaciones sobre las figuras geométricas y problematizan aspectos de la enseñanza de la geometría en la escuela primaria. Entendemos que la exigencia de construir la representación de una figura dada requiere analizarla, inspeccionar sus elementos para seleccionar algunos que se consideren relevantes para concretar la construcción en función de los datos que se ofrecen, establecer relaciones con los otros para imaginar la sucesión de pasos que lleven a “completarla”. Estos procedimientos, en diferente medida según las condiciones en las que se realicen, ponen en funcionamiento una estructuración de relaciones, favoreciendo que se entablen dependencias, jerarquías y equivalencias que contribuyan a internarse en prácticas deductivas (Sadovsky et al., 1998).
Dos supuestos orientan la concepción del Seminario de geometría: el papel productivo de las construcciones geométricas y el de las relaciones geométricas que se van explicitando al tomar en cuenta las herramientas que se utilizan. Nuestra intención didáctica es que los y las docentes-estudiantes puedan concebir una representación -el dibujo- como el conjunto de las relaciones de los elementos que caracterizan a la figura. A su vez, la utilización del programa GeoGebra permite movilizar algunos aspectos conceptuales, diferentes de los que se ponen de manifiesto en un entorno de lápiz y papel. Se considera didácticamente productivo detenerse en las relaciones entre ambos entornos.
En este artículo presentamos y analizamos dos episodios acontecidos en las primeras clases que interpretamos en términos de tensiones entre las prácticas geométricas usuales de los y las docentes-estudiantes bajo el entorno del lápiz y papel y las demandadas por el uso de un software de geometría dinámica; en particular, aquellas referidas a la inclusión del arrastre de los elementos que forman parte de un dibujo elaborado con GeoGebra. En el primero de ellos se muestra el modo en que se caracteriza en la clase un dibujo realizado con GeoGebra -cuando se considera la posibilidad de mover sus elementos y aún no se ha establecido algún criterio para corroborar si un dibujo resulta o no pertinente como representante de una figura- a partir de la discusión colectiva.
En el segundo episodio se analiza una posición crítica de una docente-estudiante poniendo en tela de juicio los fines didácticos del movimiento que, en la perspectiva de los profesores del Seminario, trae aparejado el uso del programa GeoGebra. Nos interesa destacar principalmente los modos en que es posible concebir el arrastre en las primeras clases donde se incluye el movimiento de los dibujos elaborados con GeoGebra, como asunto de negociación necesaria con los y las docentes-estudiantes. Se espera poder atribuirle un sentido al movimiento asociado a la producción de propiedades de las figuras y, al mismo tiempo, a las condiciones de funcionamiento del programa.
CONTEXTO Y METODOLOGÍA
Las clases del Seminario involucraron el planteamiento de diversas tareas y la resolución de diferentes problemas geométricos utilizando GeoGebra. Estos problemas fueron seleccionados en función de los conocimientos geométricos que hipotéticamente contribuirían a movilizar.
En la tabla 1 donde se presentan los enunciados de los primeros problemas del Seminario junto a los objetivos de cada uno a fin de explicitar este primer recorrido transitado por los y las docentes-estudiantes.
Tabla 1 Tabla con el enunciado y los propósitos de los 5 primeros problemas del Seminario
| N° | Enunciado | Objetivos |
|---|---|---|
| 1 | Construyan una recta y un punto que no pertenezca a ella. Tracen una recta paralela y una perpendicular a la recta que pasen por ese punto. Analicen qué ocurre al mover alguna de las rectas o alguno de los puntos. | − Indagar sobre cuáles son los conocimientos disponibles de los y las docentes-estudiantes sobre el uso del programa GeoGebra y en particular de la noción de arrastre. − Estudiar las diferencias entre las construcciones que mantienen invariante el paralelismo y la perpendicularidad y las que no. |
| 2 | Dibujen tres circunferencias usando, en cada caso, las herramientas Circunferencia (centro, punto), Circunferencia (centro, radio) y Compás. Posteriormente analicen qué se puede mover en cada caso y por qué. | − Estudiar las similitudes y diferencias -frente al movimiento- de las tres herramientas mencionadas, que permiten trazar circunferencias. |
| 3 | Dibujen un segmento. Dibujen luego otro segmento que mida el doble que el primero de manera tal que al mover alguno se preserve la relación “ser el doble”, sin usar la opción de medir. Entreguen por grupos todos los ensayos realizados. | − Analizar la dependencia entre dos objetos con la finalidad de que la relación “ser el doble” se mantenga invariante al mover cualquier punto libre de la construcción. |
| 4 | Construyan un cuadrado. Entreguen por grupos todos los ensayos realizados. | − Indagar sobre si los y las docentes-estudiantes creen necesario que la construcción soporte el arrastre para luego discutir en la puesta en común las diferentes posturas. − Trabajar en torno a la argumentación sobre por qué la figura construida resultó ser un cuadrado. |
| 5 | Construyan un rectángulo de manera tal que al mover cualquiera de sus elementos, siga siendo rectángulo. | − Plantear explícitamente el desafío de construir un rectángulo que soporte el arrastre. − Trabajar en torno a la argumentación sobre por qué la figura construida resultó ser un rectángulo. |
El Seminario transcurrió durante un cuatrimestre. Las clases fueron semanales, de tres horas de duración cada una de ellas. En todo momento había dos profesores a cargo, sin ninguna diferenciación en sus roles. Dichos encuentros se grabaron en audios y/o videos y luego se transcribieron en archivos de texto. Además, los y las docentes-estudiantes les entregaron a los docentes todas las producciones realizadas tanto en GeoGebra como con lápiz y papel.
En cuanto al desarrollo de las clases, en general, había un primer momento de trabajo grupal y luego una puesta en común en torno al trabajo realizado. Para esta segunda instancia, mediante un proyector, a veces los y las docentes-estudiantes les dictaban el proceso de construcción a los profesores y ellos iban reproduciendo en la pantalla los pasos; otras veces, directamente un representante de cada grupo conectaba su computadora en el cañón para mostrar su producción.4 Al finalizar cada clase, una pareja realizaba una síntesis de esta cuya lectura colectiva iniciaba la clase siguiente. Esta síntesis constituía un punto de partida para identificar las ideas sostenidas, eventualmente ampliarlas y retomarlas para continuar el trabajo o reformularlas en función de nuevas relaciones identificadas. Las sucesivas síntesis permitían hilvanar una historia de las ideas del grupo que constituía una referencia para volver a consultar.
A raíz de los problemas trabajados en el Seminario se desarrolló un conjunto de interacciones tanto entre los y las docentes-estudiantes, como entre ellos y los profesores. Hemos seleccionado algunas de dichas interacciones, que denominamos episodios, para su análisis. Tenemos como fin compartir las tensiones emergidas, el sentido que fue adquiriendo el arrastre y los procesos de negociación sobre el mismo. La selección se realizó en función de los intercambios a partir de los cuales se promovió la elaboración de un criterio que permita considerar pertinente la construcción de un dibujo -representante de una figura- asociado con la idea de “soportar el arrastre” (Arzarello et al., 2002; Laborde y Capponi, 1994; Restrepo, 2008).
Algunos y algunas docentes-estudiantes plantearon cierta resistencia a la consideración del movimiento como una nueva condición de trabajo para el estudio de propiedades de las figuras en el marco del uso de GeoGebra. Sobre estas tensiones, el análisis de algunas construcciones que se deforman al mover algunos de sus puntos libres, el estudio de ciertas propiedades puestas en juego y los debates que se desarrollaron en las discusiones colectivas donde se definieron -para nosotros- nuevos conceptos, se basa este artículo.
REFERENCIAS TEÓRICAS
Hemos considerado diferentes referencias para llevar a cabo la selección y el análisis de los episodios originados en la clase del Seminario.
En primer lugar, tomamos en consideración algunos trabajos que dan cuenta de la complejidad de los procesos de enseñanza y aprendizaje de contenidos geométricos (Berthelot y Salin, 1993; Sadovsky, et al., 1998). En particular nos centramos en aquellos que intentan recuperar para el ámbito escolar algunas prácticas centrales de los modos que históricamente han caracterizado la producción de conocimiento geométrico, entre otros: el desarrollo de procesos deductivos para dar cuenta de la validez de las relaciones que se establecen, la articulación entre el trabajo empírico y el deductivo, el papel que juegan los dibujos como promotor del análisis de las propiedades de las figuras, etc. (Duval et al., 2004; Perrin-Glorian y Godin, 2014).
En segundo lugar, nos nutrimos de diferentes trabajos donde se estudian las limitaciones que encuentran muchos docentes para lograr otorgar sentido a la enseñanza de la geometría (Alatorre y Sáiz, 2009; Itzcovich, 2005). Tanto en su experiencia escolar como en su formación inicial, la perspectiva que elaboran los maestros y las maestras de escuelas primarias sobre la enseñanza de esta rama de la matemática, en general, queda asociada principalmente a un con-junto de definiciones, afirmaciones y vocabulario que se aplican a ciertas figuras, sin haber tenido la oportunidad de analizar el valor formativo que podría tener su enseñanza en la escuela primaria (Fregona, 2005; Sadovsky et al., 1998). Asimismo, según nuestra propia experiencia en el trabajo con maestros y maestras en formación docente continua, el sentido dado a las construcciones geométricas remite más a procedimientos a seguir que a identificar las relaciones entre los elementos de la configuración geométrica. Desde esta perspectiva se suele privilegiar entonces un trabajo empírico sobre los dibujos en desmedro del acceso a la validez de las relaciones mediante un razonamiento deductivo. Esta última consideración pone en el centro la complejidad de las relaciones entre dibujos y figuras. Consideramos que un dibujo es una marca, un trazo, en tanto que la figura es el objeto abstracto, teórico que resulta representado por dicho dibujo (Parzysz, 1988).
Por otro lado, compartimos la idea de que un trabajo vinculado a las construcciones geométricas, a partir de ciertos elementos, favorece el pasaje desde una posición perceptiva -apoyada fundamentalmente en la observación- a una posición productiva apoyada en el análisis y el establecimiento de relaciones que caracterizan a las figuras geométricas representadas (Duval et al., 2004; Sadovsky et al., 1998). Entendemos por construcción geométrica a la representación que cada sujeto elabora de una figura geométrica que se propone construir, en la que usa instrumentos para hacer ostensivas propiedades de la figura. Esta representación está condicionada por los conocimientos que disponga quien la produce.
En esta misma perspectiva, adoptamos la idea de que el trabajo alrededor de las construcciones geométricas puede favorecer la puesta en juego -explícita o implícita- de algunas de las relaciones que caracterizan a las figuras asumiendo que las diferentes maneras de gestionar las construcciones en la clase supondrán distintas formas de desplegar el conocimiento geométrico (Sadovsky, et al., 1998).
También hemos considerado algunas investigaciones que estudian la inclusión de programas de geometría dinámica para la enseñanza de la geometría. A lo largo de los años, la noción de arrastre se ha ido profundizando y resignificando. Algunos investigadores (Arzarello et al., 2002; Olivero, 2003; Restrepo, 2008) plantearon diferentes usos y sentidos del desplazamiento, por ejemplo, el arrastre para validar o invalidar una construcción (prueba del arrastre).
Al mover un dibujo -que representa a cierta figura- realizado en un programa de geometría dinámica, a partir de sus puntos libres, interviene una nueva variable que no está presente en lápiz y papel: el tiempo. En consecuencia, es posible considerar sólo la posición inicial o final, o toda una familia de dibujos resultante del movimiento. En el primer caso se involucra una mirada discreta. Esta perspectiva, que Olivero (2003) denomina foto-desplazamiento, no focaliza en el proceso de cambio del dibujo original. Por otro lado, al segundo caso Olivero lo llama cine-desplazamiento. Esta mirada continua, creemos, potencia el análisis de los invariantes de la figura, en función de cierta intencionalidad docente. Posteriormente, Restrepo (2008) estudiando la génesis del desplazamiento utiliza estas caracterizaciones del movimiento en su proyecto de investigación y las relaciona con el desplazamiento para validar o invalidar una construcción. Según la investigadora, el movimiento para validar una construcción debe observarse continuamente y, por lo tanto, debe utilizarse una visión de cine-desplazamiento. Por el contrario, cuando se pone en juego un desplazamiento para invalidar una construcción, como el objetivo es encontrar una configuración particular de la construcción, el desplazamiento se utiliza de manera discreta, por lo tanto se involucra un foto-desplazamiento.
La posibilidad de movimiento o arrastre genera una expectativa sobre el resultado de las decisiones tomadas: si el dibujo se deforma o no, si sigue siendo lo que se intentaba dibujar o se desarma. Hipotetizamos que la “sorpresa” (Arcavi y Hadas, 2003) abona al análisis de las relaciones entre las propiedades de la figura, las herramientas utilizadas y las relaciones geométricas subyacentes.
Episodio 1 “Siempre” o “a veces”, esa es la cuestión: reflexiones y análisis a partir de las interacciones sucedidas en un espacio de discusión colectiva.
Cuando los y las docentes-estudiantes ingresan al aula del Seminario de Geometría, saben que su desarrollo trata sobre problemas de geometría y de su enseñanza. Desde la primera actividad se propicia el uso de GeoGebra, que algunos y algunas docentes-estudiantes nunca han utilizado. En consecuencia, las primeras interacciones con el software conjugan el aprendizaje de este recurso con el de algunas relaciones geométricas.
Como se ha mencionado en el apartado Contexto y Metodología, el primer problema del Seminario tiene por finalidad revisar las nociones de paralelismo y perpendicularidad y al mismo tiempo comenzar a explorar el funcionamiento del programa.
Problema 1
Construyan una recta y un punto que no pertenezca a ella. Tracen una recta paralela y una perpendicular a la recta que pasen por ese punto. Analicen qué ocurre al mover alguna de las rectas o alguno de los puntos.
Las resoluciones que algunos y algunas docentes-estudiantes elaboraron se apoyaron en el uso de las herramientas que GeoGebra habilita (Recta Paralela y Recta Perpendicular) y que garantizan que, al mover la recta original, se preserva el paralelismo y la perpendicularidad, tal como esperábamos. El docente-estudiante Vito, cuando abrió el programa, obtuvo en la pantalla una representación de ejes cartesianos y una cuadrícula. En esa ventana trazó una recta con la herramienta Recta por dos puntos (A y B) apoyándose en una de las líneas horizontales de la cuadrícula. Luego ubicó dos puntos C y D, fuera de la recta, pero sobre “vértices de la cuadrícula”, formando un “cuadrado”. Después, trazó una recta “paralela” por D y C usando la herramienta Recta, como se observa en la figura 1.

Figura 1 Construcción de Vito tomando como referencia la cuadrícula. https://www.geogebra.org/m/qknusad6
Analicemos el procedimiento de Vito y los conocimientos puestos en juego. Sabiendo que la cuadrícula está conformada por rectas paralelas y perpendiculares, la utilizó como referencia. En consecuencia, no recurrió únicamente a su percepción para trazar la paralela, sino que apeló a una relación reconocida por él, disponible en el programa GeoGebra. Es decir, al no soportar el arrastre, podemos considerarla una construcción blanda (Healy, 2000). Sin embargo, no fue realizada “a ojo” sino sostenida en propiedades de la cuadrícula.
Este procedimiento se puso en cuestionamiento con toda la clase y se confrontó con la construcción de su compañera Jésica, quien usó la herramienta Paralela. Una vez que Vito compartió su estrategia, se generó el siguiente diálogo:5
| Profesor 1: | ¿Las rectas [que construyó Vito] son paralelas? |
| Jesica: | Sí, son paralelas porque coinciden con los ejes, coinciden con la cuadrícula. Pero lo que tiene [mi construcción] es que después, cuando vos pinchás y movés las primeras [rectas que dibujé] siempre siguen siendo paralelas. |
| Profesor 1: | (Señala las rectas dibujadas por Jésica) ¿Éstas? |
| Jesica: | Claro. Y en el segundo caso [en la construcción de Vito], cuando vos muevas una [recta]… |
| Profesor 1: | (Explora la construcción de Jésica moviendo los puntos libres) Este punto las rota…este otro punto también las rota. (Luego el profesor muestra en la pantalla la construcción de Vito) ¿Y a estas rectas que les tendría que pasar al mover los puntos libres? |
| Jesica: | Y en estas no tendría que pasar. |
| Vito: | Creo que tendría que tener una opción para medir qué distancia de acá (señala el punto A) a acá (señala el punto C) y de acá (señala el punto B) a acá (señala el punto D). |
| Profesor 2: | (El profesor 2 se dirige al profesor 1) Sí. ¿Por qué no les mostrás cómo se hace [para encontrar la distancia entre dos puntos usando GeoGebra]? |
Si bien Jésica es una de las docentes-estudiantes que había realizado la construcción apelando a la herramienta Paralela, admite que la construcción de Vitose apoya en la cuadrícula; es decir, entiende que hay una cierta relación puesta en juego, pero que, al no haberse planteado explícitamente, no ha de conservarse.
En esta confrontación entre la estrategia de Jésica y la de Vito se puede ver la diferencia entre los conocimientos que pusieron en juego cada uno en su construcción, teniendo en cuenta su vínculo con el trabajo geométrico tanto en lápiz y papel como con el GeoGebra. Jésica, al ya tener un contacto con el programa, estaba pensando en el movimiento y anticipando que la construcción de Vito no iba a preservar el paralelismo. En cambio, Vito, necesitaba apoyarse en la medición para ver si se verificaba una propiedad que él conoce y que debía cumplirse. Esto lo podemos inferir a partir de su última intervención cuando quiso comprobar el paralelismo de las rectas midiendo las distancias entre A y C y entre B y D.
Es decir, mientras Jésica había incorporado el arrastre como una forma para verificar que las rectas siempre eran paralelas (Restrepo, 2008), Vito recurrió a la medición para garantizar que las distancias CA y DB eran iguales. Esto le permitió inferir que las rectas debían ser paralelas. Enfatizamos en el término “siempre” porque es la primera vez que aparece en la clase y va a tener un rol importante en el acercamiento al entorno de la geometría dinámica.
Coincidimos con Suory-Lavergne (2011) en la importancia de poner a discusión las construcciones blandas que realizan los y las estudiantes para luego analizar las propiedades involucradas en ellas e interpretar por qué se desarman y así poder confrontarlas con las construcciones que soportan el arrastre -denominadas robustas- (Healy, 2000).
El diálogo continuó del siguiente modo:
| Laura: | (La docente-estudiante se dirige al profesor 1 y hace referencia a la construcción de Vito). ¿Y podés mover una de las paralelas a ver si se mantiene eso? |
| Profesor 1: | (El docente le pregunta al resto de la clase) Y si muevo los puntos libres, ¿se va a mantener o no el paralelismo? |
| Jésica: | Y no… |
| Sandra: | Seguro que no. |
| (El profesor 1 mueve los puntos de la construcción de Vito y se visualiza que no se preserva el paralelismo entre las rectas). | |
| Eugenia: | Porque no tiene la función “paralela”. |
| Jésica: | No le diste la orden de ser paralela. |
| Julia: | [En la construcción de Vito] La condición paralela está…Lo que pasa es que no estás usando el botón que hace que de la primera recta [se pueda construir la segunda]. No fuiste a buscar una aplicación que se llamaba “paralela”. [En cambio en la de Jésica], buscaste una función paralela a esa, entonces ya después el programa toma en función a todo ese… te sigue manteniendo el sistema desde la primera recta base. |
En este último fragmento queremos destacar dos cuestiones. Por un lado, la acción del docente que invitó a anticipar qué iba a ocurrir con la construcción de Vito al mover los puntos. Entendemos que esta anticipación resulta un recurso que podría favorecer cierta conceptualización (Sadovsky, et al, 1998). Al mismo tiempo abona a la discusión sobre la conservación de las propiedades a través del movimiento (Gómes, 1999). Por otro lado, se destaca la noción de independencia y dependencia, aspecto que genera una ruptura con relación al trabajo usando lápiz, papel e instrumentos de geometría. Es decir, si se construye la paralela recurriendo a la herramienta Paralela, debe interpretarse que el dibujo que se genera tiene elementos independientes (puntos libres) y otros dependientes (que pueden ser puntos semilibres6 -sobre objetos- o puntos fijos -que se mueven al mover otros elementos de la construcción). En este caso, Julia habla de la “recta base”, identificando a la misma como la recta de la cual dependen los objetos construidos a continuación.
Luego se abrió la discusión sobre si las rectas “de Vito” eran o no paralelas:
| Profesor 2: | Pero entonces hay una cosa ahí que es medio rara para la historia del trabajo geométrico nuestro. ¿Podés Rodo (haciendo referencia al profesor 1) volver esta recta acá a su lugar original? Que Vito había armado…Ahí está: serían paralelas esas dos, así como están… ¿En función de qué? |
| Sandra: | De las distancias. |
| Vito: | Falta algo, medimos la distancia entre dos puntos y se tendría que mantener la distancia entre esos otros dos puntos. |
| Profesor 2: | Vos hiciste algo extra: la máquina me las toma sobre los ejes, sobre la grilla. Por lo cual, para la máquina la grilla son líneas paralelas. ¿Por qué uno podría decir que esas dos [rectas] que sugirió Vito no son paralelas? |
| Profesor 1: | (Narra lo que hace en GeoGebra) Ahí lo medí. AC mide 1 y BD… |
| Eugenia: | Sí, mediste. Y da uno y uno y la distancia siempre es uno… |
| Profesor 2: | Y, pero ellas están diciendo que si movés una… |
| Eugenia: | Ah, bueno, pero yo no...pero sin mover. |
| Profesor 2: | Rompe el paralelismo. |
| Eugenia: | Así como está [la configuración] digo… |
| Jésica: | Claro, no es que no es paralela… |
| Eugenia: | Así como está podés comprobar que son paralelas, si las querés mover es otra cosa. |
| Jésica: | Para mí no es que no es paralela, sino que no mantiene la condición…después. O sea, ahí son paralelas, pero después… |
| Profesor 2: | Entonces, ¿son paralelas o no son paralelas? |
Nuevamente aquí se produce una diferencia entre los conocimientos de Eugenia y los de Jésica. Las docentes-estudiantes interpretaron de manera distinta la invitación del profesor sobre cómo asegurar que las rectas en cuestión eran paralelas. Al igual que Vito, Eugenia apeló a sus conocimientos geométricos dentro del entorno del lápiz y papel argumentando el paralelismo mediante las distancias iguales. Cuando el profesor mencionó el desplazamiento, su respuesta fue “si las querés mover es otra cosa”. Mientras que Jésica nuevamente estaba pensando en el movimiento; esto se infiere de la frase “sino que no se mantiene la condición...después”. Lo interesante de la palabra “después” es que trae aparejada la noción del tiempo. Jésica no dudó del paralelismo de las rectas, pero para ella lo eran en ese momento, luego no necesariamente lo serían. El sentido que le otorga cada una al “después” provienen de diferentes conocimientos.
Con este episodio queremos mostrar un debate que se generó en torno al movimiento, sobre la conservación -incluso parcial- o no del paralelismo al trabajar con un programa de geometría dinámica, negociando ciertas condiciones de su funcionamiento. Producto de las interacciones tanto entre pares como con los docentes, se produjo una confrontación entre dos estrategias: una que soportaba el arrastre y otra que no.
En la clase no se aceptó de entrada la estrategia de Jésica ni se invalidó la de Vito. Se hizo una comparación entre las mismas teniendo en cuenta los conocimientos puestos en juego (en ambas hay propiedades que las sostienen) y las cuestiones tecnológicas involucradas en cada una. Finalmente se resaltó la de Jésica por sobre la de Vito en términos del “siempre”, es decir, las rectas son siempre paralelas para todo movimiento que se le impregne a la construcción.
En el aula emergieron diferentes características de las construcciones realizadas en GeoGebra que, en la síntesis de la clase elaborada por Vito y Sandra, describieron de la siguiente manera:
“Se establece la diferencia entre ser y estar en relación con un comentario respecto de las dos rectas paralelas construidas con la cuadrícula en la primera clase.
SER: habla de siempre, se preservan las propiedades frente al movimiento.
ESTAR: hace referencia a un momento determinado como si fuera una ilusión óptica donde no funcionan las relaciones.
En el ensayo de Vito, las rectas están paralelas, no son paralelas.”
Notemos la función de la síntesis a la que hicimos referencia en el apartado Contexto y metodología. Efectivamente, al enfrentarse con la necesidad de elaborar un texto que dé cuenta de lo sucedido en clase en términos conceptuales, Vito y Sandra ponen en juego los términos ser y estar -utilizados en el aula- para distinguir las dos construcciones y los ponen en relación con el siempre y a veces. Aquí podemos ver cómo tuvo que ser necesario recurrir a textos que involucran el movimiento. La interacción entre el uso de las palabras, el arrastre, los gestos y los dibujos ocupa un rol importante en la comunicación matemática de las y los estudiantes cuando se trabaja en un entorno de geometría dinámica (Ng, 2014).
Episodio 2 “¿Y qué importa que se mueva?” Reflexiones y análisis a partir de las interacciones sucedidas en un espacio de discusión colectiva.
En el cuarto problema del Seminario se propone la construcción de un cuadrado con GeoGebra donde intencionalmente no se hace referencia al movimiento, de manera tal que cada docente-estudiante le dé, al mismo, el sentido que considere en este trayecto de la cursada.
Laura y Eugenia desarrollaron una construcción, que se observa en la figura 2.
Como se puede notar accediendo al link, el paralelismo y la perpendicularidad se preservan, pero al mover algunos de los vértices, el cuadrado se deforma formando un rectángulo.
En un debate colectivo sobre esta construcción se desarrolló el siguiente diálogo:
| Eugenia: | A mí lo que me pasa es que, por ejemplo, con lo que hacíamos el otro día ¿no? Armar un cuadrado… Bueno, podés armar un cuadrado, de manera que se te desarme cuando lo movés. Pero es un cuadrado. |
| Profesor 2: | Está cuadrado, no es un cuadrado. |
| Eugenia: | Para el GeoGebra, porque si yo le saco una foto ahí, decimos todos que es una representación de un cuadrado ¿o no? |
| Profesor 2: | Sí |
| Eugenia: | GeoGebra viene a poner otra condición que es: bueno, lo tenés que poder mover sin que se desarme. Lo que me hace ruido es que rompe... |
| Profesor 1: | Sí, sí. Es un contrato nuevo… |
| Eugenia: | ¡Claro! Eso. |
En este extracto se pone en evidencia la tensión entre las condiciones de trabajo con lápiz, papel e instrumentos de geometría y las que, de alguna manera, propician el uso de GeoGebra, a partir del movimiento. Entendemos que esta docente-estudiante, está acostumbrada a un tipo de trabajo en donde lo perceptivo sigue primando, aunque identifique ciertas propiedades. Si bien en el discurso se manifiesta la necesidad de hacer explícitas las relaciones que se ponen en juego al realizar una construcción, ella destaca que, visualmente, se está representando un cuadrado, sin importar el movimiento. En términos de Olivero (2003), tuvieron en cuenta un foto-desplazamiento. Es decir, a esta pareja de docentes-estudiantes le importa el estado inicial y el estado final del dibujo, con la intención de lograr una figura determinada.
Este diálogo continuó del siguiente modo:
| Eugenia: | Porque cuando dibujás un cuadrado a la manera: segmentito, segmentito, ángulo, también estás poniendo en juego propiedades…Estás eligiendo ángulos rectos, estás eligiendo segmentos iguales… Pero ese se desarma. Es otro código en Geo-Gebra |
| Jésica: | Pero para que no se te desarme, vos tenés que seguir poniendo otras propiedades; o sea, por ejemplo… |
| Eugenia: | Claro, más propiedades… |
| Jésica: | No te puede faltar ninguna propiedad para que ese cuadrado no se desarme, si te falta una, ya se desarma. Lo tocás en alguno de los vértices y se desarma. Tenés que poner en juego sí o sí que estén todas las propiedades presentes... |
Eugenia hace un comentario que nos interesa destacar y que parafraseamos así: una construcción que se deforma puede estar apoyada en propiedades geométricas. Para ella, el hecho de no soportar el arrastre está vinculado a un código de GeoGebra, a una cuestión tecnológica y no geométrica. En relación con este asunto, notemos que tanto Eugenia como Jésica mencionan que para lograr que una construcción no se “desarme” hay que usar más propiedades o poner en juego todas las propiedades presentes en la figura, afirmación que refleja la necesidad de generar condiciones para trabajar la noción de “definición de figura”, en este caso del cuadrado. Compartimos con Zazkis y Leikin (2008) en este punto que “las definiciones de conceptos matemáticos, las estructuras subyacentes de las definiciones y el proceso de definir resultan componentes fundamentales del conocimiento de la materia de los profesores de matemáticas” (p. 133).
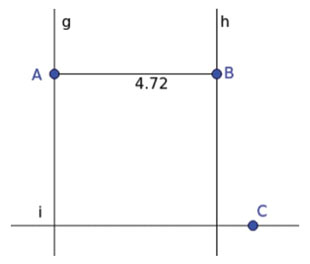
Analicemos la construcción de las docentes-estudiantes. Primero construyeron un segmento AB utilizando la herramienta Segmento. Es decir, tanto A como B son puntos libres. Luego, utilizando la herramienta Perpendicular, trazaron dos rectas perpendiculares (g y h) al segmento, una que pasa por A y otra por B, como se muestra en la figura 3.
Se puede observar que utilizaron la herramienta Distancia para medir la longitud del segmento AB. Hasta aquí, se tiene una construcción que no se deforma frente al movimiento, ya que al mover A, B, g o h, las propiedades involucradas se siguen preservando. Veamos qué ocurre a continuación.
En el siguiente paso trazaron una recta perpendicular a g, utilizando nuevamente la herramienta Perpendicular, que pasa por un punto C. Este punto C no está ubicado en ninguna de las rectas perpendiculares al segmento AB; es un punto libre que puede moverse por toda la pantalla, como se puede apreciar en la figura 4.
Pareciera ser que querían garantizar los cuatro ángulos rectos (o la perpendicularidad) vía las herramientas.
A continuación, recurrieron a la siguiente idea, que nos parece muy interesante: usando la herramienta Segmento de longitud dada trazaron un segmento con un extremo en A y luego ingresaron en la casilla que abre el programa la leyenda “AB”. Es decir, lograron un vínculo entre el segmento AB y el nuevo segmento AE (figura 5).

Figura 5 trazado del segmento AE mediante la herramienta Segmento de longitud dada. Al mover A o B, las longitudes de AE y AB se mantienen iguales.
Finalmente, ubicaron a “ojo” el punto E sobre la recta g, y luego movieron C para que la recta i (paralela a AB que pasa por C) pasara por E.
Extraigamos algunas conclusiones de esta construcción. Al mover los puntos A, B o C (o el mismo segmento AB) se preserva la perpendicularidad y el paralelismo entre las rectas. Es decir, los ángulos marcados en la figura 6 son siempre rectos, o lo que es lo mismo, ABFD es un rectángulo que soporta el arrastre.
Las docentes-estudiantes usaron herramientas para asegurarse que ABFD sea siempre un rectángulo. Aunque luego, para tener el caso particular del cuadrado no apelaron a las herramientas pertinentes, sino que movieron algunos puntos de la construcción, primero E y luego C para obtener dicha figura. Sin embargo, como pudimos observar, el dibujo no soporta el arrastre, es por esto que se considera una construcción blanda (Healy, 2000). Aquí el desplazamiento es usado en el proceso de construcción a diferencia de las robustas -las que soportan el arrastre- donde el desplazamiento generalmente es utilizado para verificar que se hayan utilizado las herramientas pertinentes (Soury-Lavergne, 2011).
Al igual que en el episodio 1 destacamos la importancia de poner a discusión las construcciones blandas (Healy, 2000) como medio para analizar las propiedades involucradas. Ahora bien, resulta interesante el planteamiento que realizan Arnal-Bairela y Oller-Marcén (2020) sobre su validez matemática:
los ajustes que se realizan a mano vienen permitidos por el entorno tecnológico, es decir no se pueden realizar cuando se realiza la construcción con lápiz y papel. Se estaría dando validez matemática a aquello que el programa es capaz de hacer. En ambos casos podría haber parejas que hacen ajustes porque el programa lo permite, sin plantearse la validez matemática una vez que es posible (y por tanto válido) tecnológicamente. (p. 94)
A nuestro entender, Laura y Eugenia tuvieron presentes las relaciones que definen al cuadrado. Primero garantizaron los cuatro ángulos rectos (aunque por las características de la construcción, finalmente algunos ángulos interiores no terminaron midiendo 90°). Luego, construyeron un segmento AE de la misma longitud que AB (es más, lograron que esta relación se preserve al mover A o B) y después lo ubicaron sobre la recta g. Finalmente movieron C para que recta i pase por E. Estos últimos dos pasos los hicieron a “ojo”. Por lo tanto, al no hacer explícitas, mediante las herramientas del programa, estas nuevas condiciones de la construcción, el cuadrado se deforma. Parafraseando a Eugenia, nos podemos preguntar: ¿las docentes-estudiantes no conocían todavía el “código” del GeoGebra? ¿O directamente no les importaba que se “desarmara” porque ellas querían lograr que fuera un cuadrado “en la foto”?
CONCLUSIONES
A lo largo de este artículo hemos intentado poner de manifiesto -así como advertir- ciertas tensiones que se pueden generar cuando se decide incluir un programa de geometría dinámica, en este caso, en el marco de un Seminario de geometría destinado a docentes de escuelas primarias que, en general, se enfrentan por primera vez a su uso.
Un primer aspecto se refiere a la cuestión del movimiento y la necesidad de negociar el sentido de preservar las relaciones mediante el arrastre, a propósito de la tarea de hacer construcciones geométricas. La posibilidad de mover los puntos que se consideraron para elaborar un dibujo con GeoGebra pone en evidencia la existencia del “tiempo” como variable; es decir, al pasar el tiempo, cambia el dibujo. Este análisis les permitió a los y las docentes-estudiantes concebir la idea de que un dibujo puede “estar” representando a una figura en un momento determinado, pero tal vez no “siempre” resulte un buen representante. Al profundizar sobre estas cuestiones en las clases del Seminario se establecieron relaciones entre las herramientas con las que se desarrolla una construcción, las propiedades -consideradas en directa relación con dichas herramientas- y la posibilidad de que efectivamente un dibujo “sea” un representante de una figura determinada.
Los conceptos “ser” y “estar” tuvieron un lugar protagónico durante el transcurso de todo el Seminario y además, los incorporamos en las discusiones con nuestros y nuestras docentes-estudiantes de las siguientes cohortes. En este sentido, creemos que estas categorías pueden ser un aporte a la enseñanza cuando se incluye un software de geometría dinámica y se problematiza la noción de arrastre.
Estos debates pusieron en el centro de la discusión la necesidad de establecer nuevas condiciones, nuevas exigencias a la hora de realizar construcciones con GeoGebra y la posibilidad de negociarlas en el aula. Como hemos visto, estas condiciones al principio pueden no ser aceptadas. A medida que se fueron identificando las potencialidades que podría adquirir el movimiento de los dibujos realizados con GeoGebra, y su relación con las propiedades que verifican ciertas figuras, la cuestión del arrastre fue “ganando terreno” en los problemas de construcción.
Un segundo aspecto que circuló a lo largo de todas las clases del Seminario es la relación entre dibujo y figura y cómo se juegan estos dos conceptos en un entorno de geometría dinámica. Este es un asunto central cuando se piensa en la enseñanza de la Geometría. En este sentido, un dibujo realizado en GeoGebra genera toda una familia de posibles representaciones de una figura identificadas mediante el arrastre. En este marco, queremos resaltar lo significativa que nos resultó la frase “con GeoGebra, estamos más cerca de la figura que del dibujo”, expresada por una docente-estudiante del Seminario. Sin embargo, es necesario relativizar la idea de “distancia” que subyace a esta afirmación ya que esta “cercanía” a la figura depende de los conocimientos disponibles del sujeto que haya realizado la construcción.
Entendemos que las características y la modalidad que adquirió el desarrollo del Seminario, los conocimientos con que contaban los y las docentes-estudiantes, su vínculo con un cierto tipo de trabajo geométrico y las interacciones que se propiciaron a raíz de la resolución de los diferentes problemas fueron algunas de las condiciones que posibilitaron la emergencia de estos asuntos que compartimos.











 nueva página del texto (beta)
nueva página del texto (beta)