1. INTRODUCCIÓN
El Estudio de Clases (EC) comenzó a desarrollarse como práctica pedagógica en la era Meiji del Japon. Su objetivo es mejorar progresivamente los métodos de enseñanza, trabajando con otros profesores para examinarse y criticarse mutua-mente las técnicas de enseñanza, pero, además, que los docentes aporten como investigadores al desarrollo de la educación de su pais (Isoda et al., 2007), por lo que se pone de manifiesto la importancia del profesor en su rol como científico. En el EC que se reporta en esta investigación se validó un diseño de clase que promueve la construcción del infinito actual. Este EC se realiza dentro del Programa de Magíster en Didáctica de la Matemática de la Pontificia Universidad Católica de Valparaíso y dada la condición mundial de pandemia, se llevó a cabo de manera virtual; esto implicó que las sesiones con los informantes acontecieran de forma sincrónicas por medio de plataformas virtuales y fueron grabadas para su posterior análisis.
Respecto al objeto matemático del EC, se tiene que la noción de infinito tiene orígenes filosóficos; el término en si, lejos de pretender cuantificar, aspiraba a calificar cualquier ente inaccesible o proceso indefinido. Esto aún ocurre en determinados contextos, pero las diversas inspiraciones racionalistas permitieron dar con la definición matemática de este concepto a finales del siglo XIX. De igual forma, la comprensión del infinito ha permitido el desarrollo de técnicas y teorías trascendentales en la evolución de la matemática.
Por añadidura, este concepto tiene un trato peculiar en el currículo y textos escolares, frente a otros conceptos matemáticos: tiene un abordaje desde una noción paramatemática y es difícil hallar referencias explícitas sobre su significado en un contexto educativo. Sin embargo, este concepto está ligado con la enseñanza de diversos tópicos habituales y obligatorios del currículo, tales como número decimal periódico, número irracional, número real, sucesión, asíntota, resolución numérica de ecuaciones, sistemas de ecuaciones y su significado geométrico, cardinal de un conjunto, inducción, etc. Aún más, este concepto comprende una variedad de dificultades y obstáculos, originados generalmente por parte de nuestra naturaleza finita que genera fuertes concepciones sobre el infinito asociadas con lo potencial, lo que conlleva en muchas ocasiones a su incomprensión (Villabona y Roa-Fuentes, 2016). Este carácter singular del infinito, y el inevitable interés que despierta en los estudiantes, ha sido la razón principal para abordar un estudio que tiene como directriz este concepto matemático.
En relación con lo anterior nos hemos preguntado, ¿Cómo abordar una situación de enseñanza virtual que promueva la construcción del infinito actual?
Además, desde una perspectiva cognitiva, Dubinsky, Weller, McDonald y Brown (2005a) plantean que el infinito actual es el objeto mental que se obtiene de la encapsulación de un determinado proceso infinito. Este objeto mental se denomina objeto trascendente ya que es el objeto que trasciende del proceso iterativo infinito del cual proviene (Brown et al., 2010). Entonces, para entender cómo los estudiantes construyen el concepto de infinito actual nace la siguiente pregunta de investigación: ¿Que estructuras mentales se evidencian en estudiantes de cuarto medio y primer año de universidad cuando se enfrentan a una actividad de enseñanza que involucra el infinito actual?
El interés de este estudio es promover la construcción de la estructura de Totalidad por medio de la operacionalización de un EC y, analizar cómo los estudiantes de educación media y primer año de universidad construyen Totalidades a partir de Procesos Iterativos.
2. PROBLEMÁTICA
Por un lado, la comprensión del infinito es compleja en cuanto es un obstáculo epistemológico y genera cierta resistencia en los aprendices (Mena-Lorca et al., 2015). Más aún, diversas investigaciones concluyen que las concepciones que tienen los estudiantes acerca del infinito son de carácter netamente potencial, es decir, generalmente están asociadas a esta idea de repetir sin fin (D’Amore et al., 2006; Montoro et al., 2016). Además, dichas concepciones son fortalecidas en los primeros años de vida escolar (Fischbein, 1978; Fischbein et al., 1979; Tall, 1980; Fischbein, 2001; Belmonte y Sierra, 2011).
Por otra parte, el currículo chileno incorporó recientemente, a los planes electivos de formación media, una asignatura electiva denominada Límites, derivadas e integrales. En dicha asignatura, se espera que los estudiantes comprendan conceptos vinculados al dominio del análisis y parte de la teoría de conjuntos; para esto, es fundamental que primero comprendan la noción de infinito actual. Pero, la asignatura en ningún momento aborda de manera explícita el concepto infinito actual, es más, este tiene un tratamiento paramatemático, por lo que las ideas que presentan los estudiantes en torno a él son asumidas a través de nociones intuitivas que desarrollan en contextos no formales de educación y podrían estar asociadas a las ideas de infinito potencial, es decir, a la noción de infinito como estructura de proceso (Dubinsky et al., 2005a).
Con relación a lo anterior, es de suma importancia que los docentes de educación media, que dictan la asignatura mencionada, se impregnen de cono-cimiento que les permita llevar a cabo una enseñanza que fomente la construcción del concepto de infinito actual. Probablemente, quienes utilizan el concepto de infinito en el proceso de enseñanza, no se detienen en su construcción, pero, “analizar situaciones relacionadas con el infinito a partir de procesos iterativos infinitos y sus objetos trascendentes, puede darle a un estudiante una herramienta formal que le permita confrontar sus propias creencias sobre el infinito” (Roa-Fuentes y Oktaç, 2014, p. 98).
Todavía más, Tirosh (1991) plantea que los estudiantes deben trabajar con situaciones de enseñanza no tradicionales acerca del infinito, que les permita cuestionarse y reflexionar sobre este concepto. Además, Villabona y Roa-Fuentes (2016) mencionan que, para comprender el concepto de límite y otros conceptos del cálculo infinitesimal, se requiere una concepción actual del infinito. En efecto, este trabajo puede ser orientador al momento de planificar una enseñanza que asuma los desafíos de los cambios curriculares actuales.
3. ANTECEDENTES DIDÁCTICOS DEL INFINITO
Debemos considerar que la idea de infinito potencial aborda el infinito como un proceso, mientras que el infinito actual es el objeto mental que se obtiene de la encapsulación de este proceso (Lakoff et al., 2000; Dubinsky et al., 2005a; 2005b). Las ideas construidas fuera y dentro del aula de matemáticas suelen suscitar inconsistencias cuando una situación requiere que los estudiantes vean este proceso como un todo terminado, pensando en las colecciones formadas por una infinidad de elementos (Roa-Fuentes y Oktaç, 2014). Además, las situaciones que involucran el infinito suelen relacionarse con paradojas, en función del contexto o de la tarea (Fischbein et al., 1979; Garbin, 1998; Garbin y Azcárate, 2000; Mantica et al, 2013; Waldegg, 1993b).
El concepto de infinito matemático ha estado concebido desde la percepción y basado en la experiencia con el mundo físico, lo que conlleva a paradojas, pues se abordan desde un mundo finito, generando una serie de confusiones y contradicciones (Ortiz, 1994). Por otra parte, D’Amore et al. (2006), proponen varias situaciones que permiten confrontar el infinito actual y el infinito potencial en estudiantes de Europa y América Central, cuyos resultados muestran que “normalmente el sentido del infinito no existe o es fuertemente obstaculizado por la intuición basada en modelos precognitivos” (D’Amore et al., 2006, p. 27).
Igualmente, Fedriani y Torino (2010) estudian la noción de infinito en la sociedad y la evolución histórica del concepto matemático, y señalan que existen muchas nociones ingenuas e intuitivas del infinito, las cuales dependerán del contexto en el que se usa.
Así también, Montoro et al. (2016), analizan las concepciones sobre la cardinalidad infinita de conjuntos numéricos, de estudiantes con distinta formación matemática (secundaria y universitaria). Esta investigación concluye que los estudiantes tienen visiones finitas muy arraigadas; dentro de ellas señalan que las justificaciones, al momento de comparar los conjuntos de los naturales, enteros y racionales, hacen referencia a que un conjunto esta incluido en el otro o que abarca más números que el otro, lo cual es válido desde un punto de vista finitista. Además, emanan fuertemente argumentos del tipo “ambos son infinitos”, haciendo alusión a una unicidad de infinito al momento de comparar un infinito numerable con uno continuo. Así mismo el infinito como cardinal esta muy lejos de ser una noción que los estudiantes adquieren por el solo hecho de estar en contacto con conjuntos infinitos de números (Montoro et al., 2016). Otros estudios, que también abordan el estudio de cardinales transfinitos, afirman que la demostración de Cantor de que hay la misma cantidad de números naturales, enteros y racionales enfrenta ideas contraintuitivas debido a que entre dos racionales siempre podremos encontrar otro racional, a diferencia del caso de los naturales y los enteros (Dehaene, 1997; Pérez-Echeverria et al., 2005). Por otra parte, Waldegg (1993a; 1996), argumenta que el hecho de establecer una correspondencia biunívoca entre un conjunto infinito y una parte propia de él, genera un obstáculo para la comprensión de los conjuntos infinitos y coincide con Mena-Lorca et al. (2015) en relación con la resistencia que se genera en los aprendices.
Además, desde la socioepistemología, Crespo y Lestón (2010) mencionan que el concepto de infinito se construye fuera de la escuela, pero una vez que ingresa al aula matemática lo hace de manera conflictiva ya que se ve influido por ideas intuitivas y extraescolares que generan obstáculos epistemológicos.
Bajo una mirada de la enseñanza, Montes et al. (2017) exploran el conocimiento del profesor acerca del infinito desde la óptica del conocimiento profesional que usan para tratarlo en el aula y mencionan que, conocer el infinito en un sentido especializado (desde el marco teórico MTSK) implica conocerlo desde una perspectiva matemática y didáctica. En la investigación, realizan un estudio de caso con un docente de educación media y superior. Concluyen que el docente no logra la comprensión del infinito actual, y que, por tanto, es muy probable que dentro de las aulas existan obstáculos didácticos. Además, mencionan que existen dos fuentes de complejidad involucradas en este concepto: la primera está asociada a la comprensión del objeto desde una perspectiva matemática, y una segunda deriva de las reflexiones que el docente establece en torno a este concepto.
Los antecedentes presentados son los aportes más relevantes encontrados; ellos generan una base de conocimiento científico, que permite visualizar el estado de avance, desde la didáctica asociados a estos temas.
Por otro lado, existen otros significativos estudios sobre el concepto infinito desde una mirada cognitiva, particularmente desde la teoría APOE, los cuales serán detallados dentro del marco teórico. Las investigaciones estudiadas, desde esta teoría, darán la perspectiva teórica del presente estudio.
4. MARCO TEÓRICO Y CONSIDERACIONES DEL ESTUDIO DE CLASES (EC)
4.1 Infinito desde la Teoría APOE
En la teoría APOE, la Descomposición Genética (DG) es un modelo de construcción de un concepto o noción matemática. La DG es un modelo cognitivo (hipotético) que se entiende, metafóricamente, como una ruta topográfica que se plantea con base en las estructuras y mecanismos mentales que están inmersos en la comprensión de un concepto matemático. En esta sección trabajaremos particularmente el modelo asociado a la construcción del infinito.
Respecto al infinito, Dubinsky et al. (2005a) relacionan el infinito potencial con una estructura mental de proceso y el infinito actual a la estructura mental de objeto, en este sentido:
El infinito potencial es la concepción de infinito como un proceso. Este proceso se construye empezando por los primeros pasos (por ejemplo 1, 2, 3 en la construcción del conjunto de los números naturales) que se refieren a una concepción acción. Repetir estos pasos (por la adición de 1 repetidamente) al infinito, requiere de la interiorización de estas acciones en un proceso. El infinito actual es el objeto mental que se obtiene de la encapsulación de este proceso. (2005a, p. 346)
Además, Dubinsky et al. (2008) recalca la importancia del trabajo con iteraciones infinitas para alcanzar la estructura de objeto del infinito, menciona que se debe dar la coordinación de procesos de iteración, y que el éxito se obtendrá cuando al menos uno de los procesos se visualice como un objeto. Por ende, lo que permitiría a un individuo pensar en un proceso iterativo infinito como un todo es aceptar la idea de que el proceso ha alcanzado a todos los números naturales, es decir, el proceso de iteración “termina”.
Asimismo, “las estructuras y mecanismos tradicionales no han sido suficientes para explicar la manera cómo los individuos intentan comprender situaciones matemáticas que involucran el infinito” (Roa-Fuentes y Oktaç, 2014, p. 74). Es así como el estudio del infinito matemático en la teoría APOE es de suma importancia, ya que han emanado nuevas estructuras y mecanismos mentales para poder explicar el proceso constructivo que implica este concepto. Específicamente, Dubinsky et al. (2013) plantearon una nueva estructura independiente, la cual se encuentra entre las estructuras de proceso y objeto; esta estructura permite que el estudiante pueda ver el proceso iterativo infinito como un todo terminado; a esta nueva estructura la denominaron Totality, que aquí se llamará totalidad.
Además, Brown et al. (2010) definen los procesos iterativos infinitos y los objetos trascendentes. Una estructura dinámica del infinito será definida como proceso iterativo infinito (entre el conjunto de los números naturales y otro conjunto cualquiera) y, los objetos trascendentes serán aquellos objetos que se abstraen de dicho proceso, “podemos pensar en el objeto trascendente como el estado al infinito del proceso iterativo que lo origino” (Villabona y Roa-Fuentes, 2016, p. 127).
Considerando la estructura de totalidad, Villabona y Roa-Fuentes (2016) plantean que, para alcanzar esta estructura, se debe considerar un nuevo mecanismo: uno que presente la particularidad de descentralizar la mirada de los elementos del proceso y enfocarla en ver el proceso como un todo terminado; es decir, este mecanismo tiene una característica distintiva, de abstracción del proceso para poder visualizarlo como una estructura estática. A este mecanismo, que normalmente se definiría como encapsulación, lo denominaron: completez. Villabona (2020) define el mecanismo completez de la siguiente manera:
Completez: Es un mecanismo mental que le permite al individuo imaginar las características que tiene la Totalidad de un Proceso infinito. El establecimiento de este mecanismo requiere de una construcción consciente de elementos fundamentales relacionados con la teoría de conjuntos: la relación entre un conjunto infinito y sus subconjuntos propios, los conceptos de cardinal y ordinal y la construcción de con-juntos infinitos con diferentes cardinalidades, específicamente, la construcción de concepciones Objeto del conjunto de los números naturales (para las totalidades de procesos iterativos infinitos) y del conjunto de los números reales (para las totalidades de procesos continuos). Estos elementos permiten la aplicación de un proceso infinito como una única transformación sobre todo ℕ o ℝ (o subconjunto de ℝ). (Villabona, 2020, p. 66)
Por otro lado, si el individuo logra encapsular el objeto trascendente podría generar acciones sobre este, por el contrario, la estructura totalidad no asegura que el individuo pueda aplicar acciones sobre ella (Villabona y Roa-Fuentes, 2016).
Para sintetizar estas ideas, se puede observar la figura 1 que se muestra a continuación:
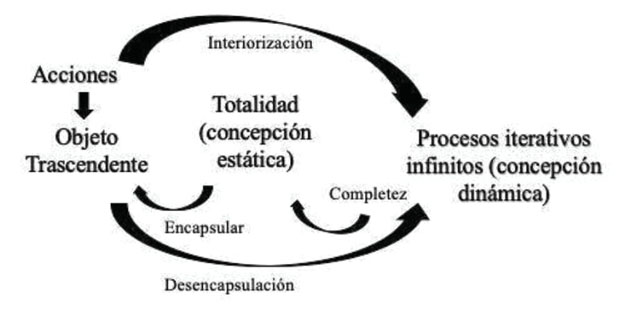
Figura 1 Estructuras y mecanismos mentales en la construcción del infinito actual. Basado en Villabona y Roa-Fuentes (2016).
4.2 Descomposición genética preliminar particular: Paradoja de las pelotas
En este apartado se analizará el modelo cognitivo para la particularidad de la actividad a trabajar. Para esto, se considerarán los trabajos de Mamolo et al. (2008) y de Roa-Fuentes y Oktaç (2014).
Roa-Fuentes y Oktaç (2014) mencionan que toda situación matemática relacionada con el infinito puede modelarse con un proceso iterativo infinito, y que, el contexto de la situación es fundamental pues determina la manera en que el individuo la aborda. Es por esto, que en esta sección se interpelará la particularidad de la actividad utilizada en esta investigación. Dicha actividad se denomina paradoja de las pelotas y es una adaptación de la paradoja de las pelotas de ping-pong presentada por Mamolo et al. (2008). A continuación, se presenta la actividad paradoja de las pelotas:
Estás a punto de realizar un experimento que durará exactamente 1 minuto, no más, no menos. Imagina que tienes un número infinito de pelotas numeradas 1, 2, 3…, y un recipiente muy grande. Tu misión será introducir las primeras 10 pelotas en el recipiente y retirar la pelota 1 en la mitad del tiempo del experimento. En la mitad del tiempo restante, introduces las pelotas de la 11 a la 20 y retiras la pelota 2.
Luego, en la mitad del tiempo restante, ingresas las pelotas de la 21 a la 30 y retiras la pelota.
Así sucesivamente, debes continuar tu tarea hasta el infinito. ¿Cuántas pelotas que-dan en el recipiente al finalizar el experimento?
En síntesis, en cada iteración se ingresan 10 pelotas y se saca una. Así, en la iteración habrán salido pelotas del recipiente; además, dicha iteración será en el tiempo
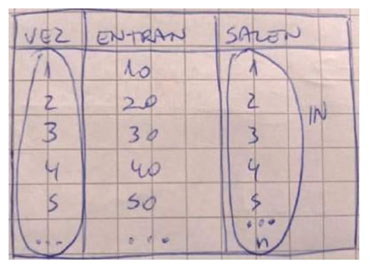
Un individuo debe comenzar realizando un número pequeño de iteraciones; una cantidad finita, de tal modo que logre establecer la manera en que se asigna un estado a cada número natural. En el primer movimiento n = 1, han transcurrido 30 segundos (o sea, aún queda la mitad del tiempo del experimento), han entrado 10 pelotas y ha salido una pelota. Ahora, para la siguiente iteración han entrado 20 pelotas y han salido 2. Con base en la realización de estas acciones, el estudiante podría interiorizarlas en procesos iterativos infinitos, desde una concepción dinámica (Dubinsky et al., 2008). Para esto, el estudiante debe construir los procesos iterativos infinitos involucrados, vale decir, la sucesión sobre los números naturales
Tabla 1 Sucesiones involucradas en la actividad Paradoja de las pelotas
| Número de iteración |
Tiempo restante para terminar el experimento |
Número de pelotas que han ingresado |
Número de pelotas que ha salido |
|---|---|---|---|
| 1 |
|
10 | 1 |
| 2 |
|
20 | 2 |
| 3 |
|
30 | 3 |
| . | . | . | . |
| . | . | . | . |
| . | . | . | . |
| n |
|
10n | n |
Con estos procesos iterativos infinitos identificados, el individuo puede establecer una coordinación entre ellos. Se puede observar que,
El mecanismo que permitirá al individuo ver al proceso como un todo terminado, es decir, como una estructura de totalidad, será el mecanismo completez. Alcanzar la totalidad dependerá de ver al menos a una de las sucesiones
4.3 Conceptos del Estudio de Clases (EC)
A continuación, se describen roles y consideraciones que deben seguir los docentes durante el desarrollo de una clase.
“Hatsumon significa hacer una pregunta clave para atraer el pensamiento del alumno sobre un punto particular en una clase” (Isoda et al., 2007, p. 88). Con la finalidad de promover o comprobar la comprensión de la tarea de la clase por parte de los estudiantes, el docente va realizando preguntas. En esta parte, se presenta la actividad paradoja de las pelotas y se realizan preguntas para asegurar el entendimiento de la actividad y para la realización de las primeras acciones.
“El Kikan-shido, que significa una instrucción en el escritorio del alumno incluye un reconocimiento deliberado que realiza el profesor de la resolución de la actividad que hacen los alumnos por si solos” (Isoda et al., 2007, p. 88). Mientras los estudiantes desarrollan la tarea propuesta, el profesor va evaluando el progreso de la resolución de la tarea de cada estudiante. Así, el docente ordena la manera en que los estudiantes exponen sus desarrollos y de cómo dirige la discusión (Isoda et al., 2007). Aquí, el docente debe reconocer las estructuras mentales que han alcanzado los estudiantes.
“Neriage se refiere a la construcción de objetos de porcelana o arcilla, e incluye los conceptos de amasar y pulir” (Isoda et al., 2007, p. 89). Entonces, en el contexto de enseñanza, este es un término metafórico que describe el proceso de pulir las ideas trabajadas por los estudiantes y obtener una idea matemática que permita generalizar la discusión de la clase. Depende del avance de los estudiantes, el docente puede hacer preguntas en relación con los procesos iterativos involucrados o la coordinación de estos o, si es que es prudente, hacia la explicación de la estructura de totalidad.
“Matome en japonés significa recapitular. Los profesores japoneses piensan que esta etapa es indispensable para cualquier clase exitosa” (Isoda et al., 2007, p. 90). Durante esta instancia el profesor retoma las ideas generales y recapitula lo aprendido en la clase. Aquí, es importante que no se fuerce la estructura de totalidad y que se resuman las estructuras efectivamente construidas por los estudiantes. En esta etapa se espera que los estudiantes expongan y defiendan sus soluciones a través de argumentos que están relacionados con las estructuras cognitivas evidenciadas previamente.
Esta es una técnica para mantener la propiedad de cada una de las resoluciones de los estudiantes. “Durante la discusión, cada método de solución es rotulado con el nombre del alumno que lo presento originalmente: ese nombre se escribe en la pizarra” (Isoda et al., 2007, p. 90). De esta manera, cada resolución es aludida usando el nombre de quien la originó.
Bansho se le denomina a la pizarra inspiradora. En la pizarra se mantiene todo lo que se ha escrito durante la clase, sin borrar si es posible. Esta idea se funda en que, para quien aprende, visualizar diferentes estrategias de forma simultánea le permite comparar de manera más fácil las resoluciones de un problema. Lo principal acá es que queden plasmadas las estructuras mentales que construyeron los estudiantes.
5. METODOLOGÍA
Esta investigación utiliza un ensamblaje entre la metodología ofrecida por el Estudio de Clase (EC) y el ciclo metodológico propuesto por la teoría APOE; a ello se acopla un diseño metodológico de estudio de caso (Stake, 2010), pues se busca comprender la particularidad y complejidad de un caso singular, particularmente las evidencias del modelo cognitivo planteado para la actividad particular propuesta (paradojas de las pelotas).
El método utilizado en este EC virtual es el método de resolución de problemas. El problema central de la clase deriva de una adaptación de la actividad paradoja de las pelotas de ping-pong trabajada en Mamolo (2008).
El proceso tomó como base el diagrama de flujo propuesto por Stigler y Hiebert (1999), pero considerando que las tres grandes fases metodológicas: kyozai kenkyu (diseno), koukai/kenkyu jyugyo (implementación) y jyugyo ken-toukai (revision) se pueden repetir tantas veces como se estime conveniente, decidimos aplicar estas fases metodológicas una vez más de lo que contiene el diagrama de Stigler y Hiebert (1999). A este proceso, se acoplaron las tres componentes del ciclo metodológico que sugiere la teoría APOE: el análisis teórico, el diseño y aplicación de enseñanza y el análisis y verificación de los datos (figura 2).
Así, el diagrama utilizado queda de la siguiente forma (figura 2):

Figura 2 Diagrama de flujo planteado para este EC. Basado en Stigler y Hiebert (1999) y en las componentes del Ciclo metodológico de investigación de la teoría APOE (Asiala et al., 1996).
En el análisis teórico se realizó un estudio histórico-epistemológico acerca de los conceptos asociados al infinito, y se estudiaron algunas descomposiciones genéticas asociadas a la noción de infinito (Roa-Fuentes y Oktaç, 2014; Dubinsky et al., 2013; Brown et al., 2010; Stenger et al., 2008; Dubinsky et al., 2005a; Villabona, 2020), las cuales se resumen en el apartado 4.1; esto permitió generar la descomposición genética de la actividad paradoja de las pelotas.
En el diseño (puntos 1, 5 y 8 del EC) y aplicación de los instrumentos (puntos 3, 6 y 9 del EC). Se llevaron a cabo las tres implementaciones
En la componente Análisis y verificación de los datos (puntos 4, 7 y 10 del EC), se llevó a cabo el análisis de las discusiones, explicaciones, argumentaciones y producciones de los estudiantes, obtenidas de las tres implementaciones. El propósito fue identificar aquellos elementos presentes de la DG preliminar particular, cuáles no se pudieron identificar, y cuáles no estaban considerados por la DG, si es que los hubo. Aquí, la DG se ejemplificará con las producciones de los estudiantes, es decir, se evidenciará la DG mostrando explícitamente los mecanismos y estructuras mentales que se evidencian en los estudiantes, para observar si se alcanza la estructura de totalidad.
Respecto de las implementaciones, todas fueron sesiones virtuales a través de la plataforma Meet, tuvieron una duración de 60 minutos y su gestión fue realizada por dos profesoras (se les denominará P1 y P2), las cuales además son investigadoras de este trabajo.
5.1 De la primera implementación
Se presentó la actividad paradoja de las pelotas tal y como fue descrita en el apartado 4.2. Se trabajo con un grupo de 6 estudiantes de cuarto año de educación media (E1, E2, …, E6).
Los estudiantes pertenecen a un colegio particular subvencionado de la región de Valparaíso. El grupo es mixto, de mujeres y hombres, cuyas edades son 18 años. Además, todos los estudiantes pertenecen a la formación diferenciada humanístico-científica del área de matemáticas y ciencias. Todos presentan conocimientos en los conceptos de límite y continuidad, y han trabajado con funciones discretas y continuas, y con sucesiones.
En relación con la gestión, ingresaron todos a una misma sala y realizaron una lectura individual de la actividad, se aclararon dudas y luego se conformaron salas grupales para llevar a cabo un trabajo colectivo (2 grupos de 3 estudiantes cada uno). Finalmente, se realizó una exposición de las ideas centrales de cada grupo y para ello se utilizó la pizarra Jamboard de Meet.
5.2 De la segunda implementación
La actividad paradoja de las pelotas sufrió una modificación en el abordaje de la variable tiempo que será explicada más adelante.
Se trabajo con un grupo compuesto por 5 estudiantes de universidad (U1, U2, …, U5) y 3 de cuarto año de educación media (Es1, Es2 y Es3). Los estudian-tes universitarios pertenecen a una universidad del norte del país y cursan primer año de licenciatura en Física. Los estudiantes escolares pertenecen a un colegio particular de la región de Antofagasta. El grupo es mixto, de mujeres y hombres, cuyas edades fluctúan entre los 18 y 20 años. Además, todos pertenecen a la formación diferenciada humanístico-científica del área de matemáticas y ciencias. Todos los estudiantes presentan conocimientos en los conceptos de límite y continuidad, y han trabajado con funciones discretas y continuas, y con sucesiones. Es justamente por este punto que la investigación abarca tanto a estudiantes de educación media como de primer año de universidad; ambos presentan los mismos conocimientos previos.
En relación con la gestión, ingresaron todos a una misma sala y realizaron una lectura individual de la actividad, se aclararon dudas y luego se conformaron salas grupales para llevar a cabo un trabajo colectivo. Un grupo lo conformaron los estudiantes universitarios y otro los estudiantes de educación media. Finalmente, se realizó una exposición de las ideas centrales de cada grupo y para ello se proyectó un archivo PowerPoint.
5.3 De la tercera implementación
La actividad paradoja de las pelotas se abordó de la misma manera que la segunda implementación. Pero, previo a preguntar por cuántas pelotas quedan en el recipiente, se solicitó a los estudiantes que establecieran una representación de la situación, el porqué de esto será explicado más adelante.
Se trabajó con un grupo compuesto por 4 estudiantes de cuarto año de educación media (Est1, Est2, Est3 y Est4). Los estudiantes pertenecen a un colegio particular de la región metropolitana. El grupo es mixto, de mujeres y hombres cuyas edades son de 18 años. Además, todos pertenecen a la formación diferenciada humanístico-científica del área de matemáticas y ciencias. Asimismo, han trabajado con funciones discretas y continuas, y con sucesiones; pero, en este caso, no han trabajado con límites.
En relación con la gestión, ingresaron todos a una misma sala y realizaron una lectura individual de la actividad, se aclararon dudas y luego se conforma-ron salas individuales de trabajo. Finalmente, se realizó una exposición de las ideas centrales de los estudiantes y para ello se proyectó un archivo PowerPoint.
6. RESULTADOS
6.1 Del Estudio de Clases y su gestión
Respecto de los roles, una vez que los estudiantes comprendieron la actividad, las Hatsumon estuvieron enfocadas, como lo decía el plan de clases, en cuestionar las pelotas que quedan dentro del recipiente. En un inicio, las preguntas estuvieron pensadas para que los estudiantes establecieran acciones: ¿Cuáles son las variables del problema? ¿Cuál es el tiempo en el primer movimiento? ¿Y en el segundo? ¿Y en el tercero? ¿Qué pelota sale en el segundo movimiento? ¿Y en el tercero?, ¿Qué valores han tomado las variables en el primer movimiento? ¿Y en el segundo movimiento?, por ejemplo. Luego, las preguntas intentan guiar a los procesos iterativos involucrados y la coordinación de estos: ¿Cómo se pueden generalizar los comportamientos? ¿De qué manera se relacionan? Finalmente, ¿Salen todas las pelotas del recipiente?, para promover la estructura totalidad.
Se pudo observar que siempre estuvo presente la resistencia en los aprendices (Mena-Lorca et al., 2015) a aceptar la idea de infinito actual, en este sentido, no aceptan que han salido todas las pelotas. Se buscó durante toda la clase la Neriage, pero siempre estuvo presente el pensamiento de infinito potencial, y considerando que “el rol del profesor no es indicar la mejor solución, sino guiar la discusión de los alumnos hacia una idea integrada” (Isoda et al., 2007, p. 90) la Matome de la clase, no llegó a ser la solución esperada de la actividad.
Por otro lado, el Kikan-shido fue muy complejo de llevar a cabo, ya que las salas de trabajo eran grupales por lo que en ningún momento se tuvo la instancia de trabajar de manera personalizada con cada estudiante. Esto produjo que ciertas maneras de abordar la actividad planteada, por parte de algunos estudiantes, influyeran más de lo necesario en otros que aún no llegaban al fondo de su reflexión personal.
Por otra parte, la organización de la Bansho fue muy compleja, los estudiantes no se familiarizaban con la pizarra Jamboard de Meet por lo que se les acomodó enviar sus producciones vía WhatsApp ya que esta es una plataforma de uso cotidiano para ellos. Este cambio produjo tardanza en la recolección y organización de las mismas. Lamentablemente, no se alcanzó a presentar una Bansho que resumiera las producciones principales de los estudiantes. Por consecuencia, la propiedad de cada una de las resoluciones de los estudiantes no se pudo realizar de manera visual, pero se intentó recalcar de manera verbal en todo momento.
Respecto de la gestión de los tiempos, estos se cumplieron a cabalidad.
Consideramos que las Hatsumon deben hacer más énfasis en las pelotas que
salen, y una vez que los estudiantes consideren esta sucesión (
Respecto a la Bansho, decidimos simplemente recolectar las producciones de los estudiantes vía WhatsApp ya que es una aplicación cercana a ellos. Pero, para agilizar la recolección y organización de las producciones, descargaremos WhatsApp Web ya que este programa permite contar con las imágenes de inmediato en el computador. Esto creemos que nos permitirá poder organizar de mejor manera la Bansho.
Respecto de los roles, esta vez las Hatsumon estuvieron pensadas para que los estudiantes noten que
Durante el trabajo grupal, los estudiantes se separaron en dos grupos: uno compuesto por los estudiantes universitarios y el otro por los estudiantes de educación media. En el momento de realizar las exposiciones de los grupos, el primer grupo que expuso fue el de los estudiantes universitarios; sus participantes mencionaron que la expresión algebraica que representa el ingreso de las pelotas es 9n y que, como el experimento dura infinitamente, se debe calcular el límite, cuando n tiende a infinito, de la expresión 9n. Por lo que concluyen que la cantidad de pelotas que hay en el recipiente al finalizar el experimento es infinita. Para dar a conocer la resolución del grupo, un estudiante proyectó su pantalla para detallar los cálculos realizados. Esta situación produjo que los estudiantes de educación media se convencieran de ese argumento, pese a que su conclusión central había sido que el recipiente quedaba vacío al finalizar el experimento.
En esta implementación, nuevamente estuvo presente la resistencia en los aprendices (Mena- Lorca et al., 2015) en aceptar la idea de infinito actual, en el sentido que son capaces de responder que salen todas las pelotas, pero igual quedan infinitas porque el proceso continúa infinitamente y son más las que han entrado que las que han salido.
De nuevo durante la Neriage se abordaron preguntas para que los estudiantes reflexionaran en torno a los cuantificadores involucrados, es decir, que concluyeran que si todas las pelotas han salido entonces ninguna queda dentro, pero en la mayoría estuvo presente el pensamiento de infinito potencial, aunque esta vez se observó la excepción de un estudiante. Específicamente, un estudiante de educación media defendió la noción de infinito actual, es decir, concluye que todas las pelotas han salido por lo que el recipiente queda vacío.
Considerando el contexto de virtualidad, el Kikan-shido fue muy complejo de llevar a cabo; solamente se lograron discusiones grupales, pero en ningún momento se tuvo la instancia de trabajar de manera personalizada con cada estudiante. Esto produjo que ciertas maneras de abordar la actividad planteada, por parte de algunos estudiantes, influyeran más de lo necesario en otros que aún no llegaban al fondo de su reflexión personal. Esto sucede principalmente en el momento en que deben dar a conocer la comprensión de la actividad; en ese momento, además de resumir la tarea que deben realizar, se aventuran a dar respuestas de la actividad, pero siempre están asociadas a nociones de infinito potencial, y, posteriormente, estas ideas quedan instaladas para el resto de la clase, pese al trabajo del Neriage.
Por otro lado, pese a tener instalado el programa para reunir las producciones de los estudiantes, la selección de las imágenes para la Bansho fue compleja ya que enviaron demasiadas imágenes, esto impidió generar una Bansho que visualizara las diferentes estrategias de forma simultánea.
Respecto de la gestión de los tiempos, estos se cumplieron nuevamente a cabalidad, por lo que consideramos están bien considerados en la planificación.
Para llevar a cabo un buen proceso de Kikan-shido decidimos hacer salas de trabajo individuales que permitan llevar un diálogo personalizado con cada estudiante, y por consecuencia poder evaluar el progreso de cada uno. Creemos que esto nos permitirá conocer cada una de las resoluciones y, con esta información, ordenar la Neriage que se dará posteriormente en la discusión grupal. Nos parece estratégico que expongan solo dos estudiantes: uno que visualice la actividad desde una mirada potencial y uno que presente nociones de infinito actual. Con esto, esperamos que se confronten estas dos miradas y que, desde el protagonismo de la sucesión de las pelotas que salen, los estudiantes puedan concluir que el recipiente queda vacío al terminar el experimento. Al mismo tiempo, para contar con solo dos producciones que representen las estrategias, estas las escogeremos previamente en la instancia de los diálogos personalizados. Creemos que nos facilitará el orden de la Bansho y para el uso de la técnica de la propiedad de cada una de las resoluciones de los estudiantes. Entonces, pese a que los tiempos de cada momento en las implementaciones anteriores se cumplieron a cabalidad, los tiempos se ajustarán en la tercera implementación. Esto, con la intención de que los estudiantes tengan más tiempo para llevar a cabo su propia resolución hacia la actividad central de la clase y, luego realizar las discusiones en conjunto.
El trabajar con salas individuales facilitó el Kikan-shido. Esta vez se pudo atender de manera personalizada a cada estudiante, según sus propias resoluciones de la actividad. Asimismo, se pudo levantar información acerca de los estudiantes que expondrían en el momento grupal. La elección de los estudiantes fue estratégica ya que se logró poner en controversia los pensamientos de infinito potencial y actual, luego, con base en esta dualidad, se dieron las discusiones grupales.
Respecto al Bansho, como se tenía claridad de los estudiantes que expondrían, se pudieron recopilar sus producciones, las cuales fueron consideradas al momento de ordenar la Bansho. Así, esta vez la Bansho sintetizó las resoluciones más significativas para la clase. Al mismo tiempo, se pudo llevar a cabo la técnica de la propiedad de las resoluciones de cada estudiante.
Respecto de la gestión de los tiempos, estos se cumplieron nuevamente a cabalidad, por lo que reafirmamos que están bien considerados en la planificación.
Se observa, en la tercera implementación, que la mayoría de los estudiantes logra una resolución correcta de la actividad propuesta para la clase. Esto nos hace pensar que las reconsideraciones tomadas: tanto para la actividad (que serán presentadas más adelante), como para la gestión, contribuyen para alcanzar el objetivo de la actividad.
Además, el trabajo en salas personalizadas, posibilitó atender de mejor manera el Kikan-shido, y esto a su vez, permitió retroalimentar a cada estudiante y organizar óptimamente su exposición. Lo expuesto, sumado a la experiencia de las primeras implementaciones, permitió que se culminara con una Bansho que resume las estrategias principales de forma simultánea, en conjunto de la propiedad del estudiante. A continuación, se presenta la Bansho resultante de la tercera implementación (figura 3):
6.2 Del Estudio de Clases y precisiones cognitivas
Una de las ideas intuitivas de los estudiantes que perduró durante la implementación, y que coincide con los estudios de Mamolo et al. (2008) acerca de la premisa que manifiestan los individuos al tratar con una paradoja similar, es que, al finalizar el experimento, hay una cantidad infinita de pelotas dentro, pues el infinito de pelotas que ingresan es más grande que el infinito de pelotas que salen. Esto se ejemplifica con lo mencionado por el estudiante E5:
| E5: | salen infinitas, pero sigue siendo menor al infinito que entra, por lo que quedan infinitas dentro. El infinito que hay dentro es más grande que el infinito que sale. |
Para que un individuo inicie con la construcción estática del infinito, es fundamental que logre diferenciar sus ideas intuitivas del conocimiento formal (Mamolo et al., 2008). En relación con esto, se pudo observar que los estudiantes se mueven entre pensamientos intuitivos y, a ratos emananargumentos formales basados en la lógica, pero finalmente los pensamientos intuitivos son los que se ven arraigados en los estudiantes al momento de concluir la implementación. Los estudiantes mencionan que el infinito de pelotas que ingresa es más gran-de al infinito de pelotas que sale.
Por otro lado, en reiteradas ocasiones, consideran la imposibilidad de completar los 60 segundos. Quine (1966, citado en Mamolo y Zazkis, 2008) plantea que, los individuos, al tratar con situaciones infinitas que involucran el tiempo, cometen el error de pensar que infinitos intervalos de tiempo implican un proceso sin fin. Estos argumentos son presentados por varios estudiantes, quienes plantean que la subdivisión del tiempo no tendrá un final y que, por tanto, el experimento no acabará. Es así el ejemplo de E2:
| E2: | pero a la vez siento que cuando el tiempo se parte en dos, esa fragmentación no se puede acabar, ¿o sí? Se hará una y otra vez, pero no se llegará a un final. |
Como se mencionó, la actividad involucra la subdivisión iterativa de un intervalo de tiempo; los individuos deben aceptar que trascurren los 60 segundos y que el experimento termina. Ante este contexto, Roa-Fuentes y Oktaç (2014) plantean que la idea de aceptar lo infinito en lo pequeño es más difícil de aceptar que el infinito en lo grande.
Por esta dificultad, hemos realizado un cambio de condiciones en la actividad propuesta; decidimos cambiar el abordaje del tiempo para la siguiente implementación. Para la implementación 2, se planteó que el experimento durará infinitamente.
Pese a que los estudiantes realizan acciones, las cuales son interiorizadas en procesos iterativos infinitos, y a que un estudiante logra dar argumentos que evidencian la comprensión del infinito desde una estructura de totalidad, al finalizar la implementación, los estudiantes retoman las ideas intuitivas que emanan en el comienzo de la implementación.
Al finalizar, el estudiante U3 resume las ideas de varios estudiantes de la siguiente forma:
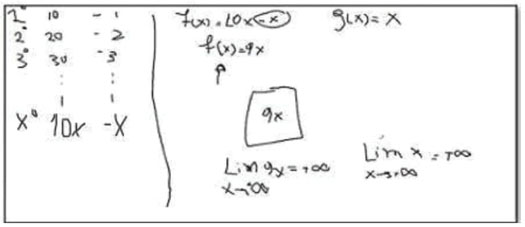
| U3: | Cada 10 pelotitas se perdía una, cuando hay 20 pelotitas ingresadas se pierden 2, cuando hay 30 se pierden 3, y así infinitamente. Entonces, si se dan cuenta siempre se cumple que para el ciclo 1, vamos a llamarle ciclo a este proceso de agregar 10 quitar 1, se pierde el equivalente al ciclo, es decir, si estamos en el ciclo 2, perdieron 2, si estamos en el ciclo 3, se perdieron 3. Por tanto, para el x-ésimo ciclo se han ingresado 10 pelotas y han salido . Entonces, podríamos llevar esto a una función, es decir, la función agregamos 10 por ciclo, 10x y le restamos una por cada ciclo, es decir, x, nos queda finalmente la función |
Se puede apreciar que los estudiantes tienen claridad de las acciones que hay en juego, y que pueden interiorizarlas en procesos iterativos infinitos, además, coordinan los procesos iterativos infinitos involucrados en la actividad. Luego, al momento de buscar los argumentos para dar respuesta con la actividad, calculan los límites de las expresiones algebraicas encontradas. Para los estudiantes, las pelotas que hay dentro se calculan por medio del límite cuando x tiende a infinito de 9x y, el cálculo de las pelotas que hay fuera, viene dado por el límite cuando tiende a infinito de x. Concluyen, después de realizar los cálculos, que hay infinitas pelotas dentro e infinitas pelotas fuera.
Los estudiantes no argumentan desde la iteración de las pelotas que salen del recipiente, por lo que no aceptan que todos los elementos del conjunto de los números naturales han sido alcanzados mediante el proceso y, por tanto, no concluyen que todas las pelotas han salido.
En esta implementación, vuelve a apreciarse la premisa de que, al finalizar el experimento, hay una cantidad infinita de pelotas dentro, pues consideran que el infinito de pelotas que ingresan es más grande que el infinito de pelotas que salen. Mamolo et al. (2008) plantean que este tipo de reflexiones se dan en los primeros momentos que los individuos afrontan situaciones similares, pero en este caso, perduran a lo largo de la implementación.
Se aprecia, al concluir la implementación, que los estudiantes generan una resistencia a aceptar que, al finalizar el experimento, salen todas las pelotas. Por lo anteriormente expuesto, para la siguiente implementación, se presenta la misma actividad a los estudiantes, pero se les solicitará que realicen una representación de la actividad y luego que respondan a la pregunta ¿cuántas pelotas quedan en el recipiente al finalizar el experimento? Adicionalmente, decidimos trabajar con el software Excel para mostrar un gran número de iteraciones. El objetivo es que, por medio de funciones de Excel, se muestre la coordinación de los procesos que hay en juego y se itere un gran número de veces
Se pudo observar también, que con el cambio de las condiciones de la variable tiempo, los estudiantes no tienen problemas para hablar del término del experimento. Ahora bien, tal y como se detalló; solo un estudiante alcanza una construcción exitosa del infinito, y esto le permite concluir que salen todas las pelotas del recipiente; el resto de los estudiantes, concluyen que al finalizar el experimento habrá infinitas pelotas dentro.
Tener una cantidad más reducida de estudiantes permitió tener más tiempo para discutir en profundidad los argumentos de cada uno de ellos. Asimismo, las sesiones individuales permitieron tener discusiones más personalizadas.
Además, promover la representación de la situación permitió que comprendieran de manera más rápida las acciones, que las interiorizaran en procesos iterativos infinitos y que los coordinaran. Asimismo, creemos que hacer hincapié en las preguntas relacionadas a las pelotas que salen y que hay dentro permiten resaltar los cuantificadores involucrados en la situación y ayudan a que el estudiante reflexione respecto a qué sucede al terminar el experimento. Esta reflexión permitió, que la mayoría, visualizaran el experimento como un todo y concluyeron que todas las pelotas salen de recipiente. A continuación, se presenta el discurso del Est3 que da cuenta de la estructura de totalidad:
| Est3: | Cuando miro las pelotas que salen del recipiente, veo que primero sale la pelota 1, después la 2 y sigo así, finalmente, puedo encontrar un instante en que va a salir la pelota 𝑛 cualquiera, entonces… salen todas! |
| P1: | ¿Y cuántas pelotas quedan dentro del recipiente? |
| Est3: | ¡No quedan pelotas en el recipiente! [risas] por ejemplo, si pienso en una pelota, siempre va a haber un instante en que va a poder salir, y no importa cuán grande sea, siempre va a haber un instante en que sale porque esa vez se relaciona con el número de la pelota que sale. Si pienso en el final de experimento, al final salen todos los números naturales, ¡o sea, todas! |
Se puede apreciar en el diálogo y en la producción del estudiante que es capaz de coordinar los procesos iterativos infinitos involucrados ya que asocia a cada pelota un instante en que ella sale del recipiente. Además, segun Dubinsky et al. (2013), esto permite que el proceso pueda verse como una transformación completa. En este caso, el Est3 observa la estructura de totalidad ya que puede ver la transformación como un todo, es decir, acepta que la convergencia de la sucesión puede ser alcanzada y esa convergencia implica que todas las pelotas han salido del recipiente.
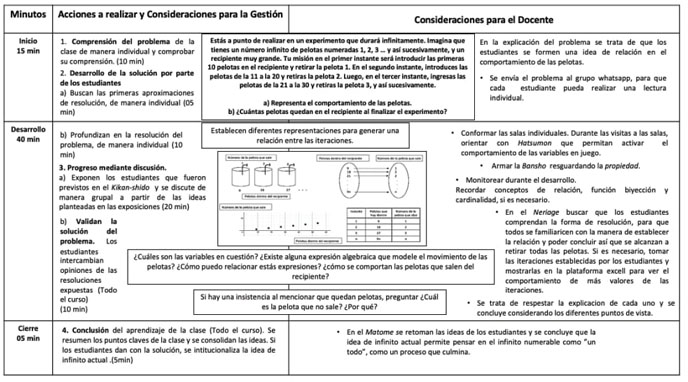
En suma, tomando en cuenta todas las reconsideraciones y los aprendizajes del proceso llevado a cabo, la propuesta final del plan de clase es la siguiente (figura 6):
7. CONCLUSIONES
Respecto a cómo abordar una situación de enseñanza virtual que promueva la construcción de infinito actual, podemos concluir que las Hatsumon deben incentivar la estructura de acción en los estudiantes y deben hacer énfasis en las pelotas que salen del recipiente, pues luego deben notar que
Adicionalmente, las modificaciones realizadas a la actividad del Estudio de Clase virtual, basadas en la teoría APOE, propiciaron que los estudiantes desarrollaran el mecanismo completez y luego lleven a cabo argumentos desde la estructura de totalidad. Para diversos autores alcanzar la estructura de totalidad significa alcanzar una construcción exitosa del infinito pues se logran construir los procesos iterativos infinitos y verlos como una totalidad (Dubinsky et al., 2005a, Dubinsky et al., 2005b; Brown et al., 2010), en este sentido, la clase propuesta promueve la construcción del infinito y así se cumple el objetivo propuesto en este estudio.
Por añadidura, el plan de clases le brinda a los estudiantes herramientas para argumentar acerca de la existencia de límites de funciones en el infinito y en un punto, ya que guarda relación con las expresiones tiende a y es, que se utilizan en relación con los límites y también, para determinar convergencia y continuidad en contextos matemáticos ya que el estudiante se enfrenta con una actividad en la que debe observar las transformaciones como un todo, es decir, debe aceptar que la convergencia de la sucesión puede ser alcanzada.
Además, este Estudio de Clases es un aporte para la comunidad de educadores matemáticos que tenemos el desafío de incorporar herramientas tecnológicas que faciliten el proceso de enseñanza y aprendizaje, con el propósito de mejorar la calidad de la educación matemática y en particular, la enseñanza del infinito.
Asimismo, se presenta un plan de clases innovador, puesto que fue realizado en un contexto de virtualidad y se pueden apreciar consideraciones técnicas y metodológicas que podrían ser de ayuda para la comunidad educativa.
A modo de proyección, nos proponemos diseñar una clase que permita mostrar evidencias de la estructura de objeto trascendente, pues es un trabajo poco explorado en el campo de la didáctica de la matemática.











 nueva página del texto (beta)
nueva página del texto (beta)