1. INTRODUCCIÓN
Los documentos curriculares y los materiales o libros de texto componen objetos de investigación en el campo de la didáctica. Los primeros porque, evidentemente, constituyen la normativa sobre lo que se debe enseñar y aprender en cada nivel educativo. Los segundos porque, en muchas ocasiones, establecen el currículo “de facto”, tal y como han señalado algunos autores (Rodríguez, 2006). Por esta razón, su análisis constituye un reflejo de los significados que se trabajan en las aulas, y por tanto, es necesario desarrollar herramientas metodológicas que lo faciliten (González y Sierra, 2004; Occelli y Valeiras, 2013; Ruiz de Gauna et al., 2013). Estos
autores señalan diversas debilidades de las propuestas editoriales. Por ejemplo, existencia de errores e imprecisiones, exceso de carácter expositivo, transmisión de una imagen positivista, sobreabundancia de tareas mecanicistas, etcétera.
La probabilidad, como parte de la matemática y base de otras disciplinas, es esencial para preparar a los estudiantes de cara a tomar decisiones adecuadas en situaciones aleatorias. Estas situaciones aparecen continuamente en la vida cotidiana del ciudadano del siglo XXI, por lo que es esencial lograr una adecuada alfabetización probabilística, entendida como conjunto de conocimientos, capacidades y actitudes que permitan al ciudadano desenvolverse frente a los fenómenos aleatorios (Gal, 2005). Esto justifica el interés y la necesidad de incluir específica-mente la estadística y la probabilidad como contenido curricular, evidenciados en diversas orientaciones internacionales (NCTM, 2000) y en muchos de los currículos escolares de los últimos años (Batanero, 2014; Jones, 2005). Estos currículos destacan, además, la importancia de la modelización, de la experimentación y de la recogida y análisis de datos, en el aprendizaje de la probabilidad (Batanero, 2005; Jones, 2005; Ortiz y Serrano, 2008). Resulta esencial que el alumnado disponga de un bagaje experiencial adecuado sobre el cual construir los contenidos, especialmente, en probabilidad, donde muchos resultados son contraintuitivos.
En esta misma línea, diversas investigaciones señalan la necesidad de tratar desde las propuestas curriculares los significados intuitivo, subjetivo, frecuencial y clásico de la probabilidad, de manera articulada y acorde a la edad de los estudian-tes y sus conocimientos previos (Batanero, 2005; Batanero et al., 2016; Batanero y Borovcnik, 2016; Jones, 2005). Cada significado da lugar a diferentes interpretaciones de la probabilidad, que, obviamente, presentan también características comunes que deben ser consideradas e incorporadas de manera gradual para lograr la construcción y comprensión de la probabilidad. Alcanzar una comprensión lo más plena posible evita, entre otras cosas, la formación de sesgos de razonamiento probabilístico. La modelización y simulación, con ayuda de software, permiten integrar y articular dichos significados en el proceso educativo, complementando la experimentación física que pueda llevarse a cabo con diversas situaciones (Batanero y Borovcnik, 2016; Ortiz y Serrano, 2008; Prodromou, 2014).
Teniendo en cuenta estas consideraciones, surge la necesidad de examinar si las directrices actuales hacen eco de las recomendaciones surgidas en el seno de la didáctica de la matemática con relación a los significados de la probabilidad. A pesar de que los estudios sobre el tratamiento de los contenidos de probabilidad en el currículo y en los libros de texto son escasos, trabajos como los de Gómez-Torres (2014), Sánchez (2009) y Vásquez y Alsina (2015), determinan que una mayoría presenta objetos matemáticos relacionados a los diferentes significados de la probabilidad, pero con limitaciones respecto a los contenidos ligados a los significados frecuencial y subjetivo. Los autores sugieren que, para una enseñanza y aprendizaje adecuado, se debería proponer una muestra representativa y equilibrada de situaciones contextualizadas a cada significado de la probabilidad.
Con base en las nociones del Enfoque Ontosemiótico (EOS) del conocimiento y la instrucción matemáticos (Godino, 2002; Godino et al., 2007), en este trabajo desarrollamos un método para analizar el tratamiento de la probabilidad en la normativa curricular, en particular, la representatividad y articulación de los diferentes significados de la probabilidad, que aplicamos en los documentos curriculares de nivel educativo secundaria en Perú (estudiantes de 12-13 años).
2. Marco teórico y antecedentes
Para llevar a cabo un análisis sistemático de los documentos curriculares, emplearemos las nociones de significado institucional y personal, configuración epistémica y configuración didáctica desarrolladas en el marco del EOS (Godino y Batanero, 1994; Godino et al., 2007) cuya potencialidad para el análisis de materiales curriculares ha sido puesta de manifiesto en trabajos previos (Font et al., 2010; Gómez et al., 2015). Estas se describen brevemente a continuación.
2.1. Significado de un objeto matemático
En el EOS se considera práctica matemática a “toda actuación o expresión (verbal, gráfica, etc.) realizada por alguien para resolver problemas matemáticos, comunicar a otros la solución obtenida, validarla o generalizarla a distintos contextos y problemas” (Godino y Batanero, 1994, p. 334). Así, el significado (institucional) de un objeto matemático queda determinado por el “sistema de prácticas (operativas y discursivas) institucionales asociadas al campo de problemas de las que emerge el objeto en un momento dado” (p. 338). En los sistemas de prácticas intervienen diversos objetos matemáticos que son clasificados según su naturaleza en: situaciones-problemas, lenguajes, conceptos-definiciones, proposiciones-propiedades, procedimientos y argumentos (Godino et al., 2007). Estos objetos no se encuentran aislados en las prácticas matemáticas, sino interrelacionados formando configuraciones ontosemióticas, pudiéndose distinguir entre configuraciones cognitivas y epistémicas, según se trate de significados personales (de los estudiantes, de profesores en formación o en ejercicio, etc.) o institucionales, respectivamente. El reconocimiento de la trama de objetos interrelacionados que interviene en dichas prácticas es necesario para gestionar los procesos de estudio matemáticos e identificar conflictos semióticos potenciales.
La noción de conflicto semiótico en el EOS es entendida como cualquier “disparidad o desajuste entre los significados atribuidos a una misma expresión por dos sujetos -personas o instituciones-” (Godino, 2002, p. 258). Si la disparidad se produce entre significados de tipo institucional (por ejemplo, entre el significado de referencia y el implementado en un libro de texto o por un profesor) se trata de un conflicto epistémico, mientras que si la disparidad se produce entre prácticas que forman el significado personal de un mismo sujeto se produce un conflicto cognitivo. Cuando la disparidad se produce entre las prácticas de dos sujetos diferentes en interacción comunicativa (por ejemplo, alumno-alumno o alumno-profesor) hablaremos de conflicto interaccional.
El análisis operativo y detallado de un proceso de estudio, en nuestro caso, el planificado en los documentos y materiales textuales curriculares, requiere ser dividido en unidades de análisis o configuraciones didácticas (Godino et al., 2014). Una configuración didáctica es “un segmento de actividad didáctica (enseñanza y aprendizaje) que se distribuye entre los momentos de inicio y finalización de una tarea o situación-problema diseñada” (Godino et al., 2014, pp. 172-173) e incluye tanto la descripción de las acciones de los estudiantes y del profesor, como de los medios planificados o usados para abordar la tarea. Permite identificar: a) el progresivo despliegue de los significados instituciona-les implementados; b) los aprendizajes y de su dependencia de los formatos de interacción que efectivamente tienen lugar; c) del uso de los recursos y del tiempo asignado (Godino et al., 2006). En Godino et al. (2006), Godino et al. (2014) o Rivas y Godino (2015) se muestra la utilidad de la noción de configuración didáctica para analizar los diseños instruccionales o describir procesos formativos.
2.2 Significados de la probabilidad
Según Hacking (1975), la probabilidad ha tenido desde su origen una doble concepción, pues se relaciona con el grado de creencia personal y con la tendencia mostrada por sucesos aleatorios al producir frecuencias relativas estables. Estas dos perspectivas principales, que se reflejan en los trabajos de los autores que han contribuido al progreso de la probabilidad, han evolucionado a lo largo de la historia en diferentes interpretaciones o significados de la probabilidad (Batanero 2005; Batanero et al., 2016; Batanero y Díaz 2007; Borovcnik y Kapadia, 2014). Actualmente, los principales significados de la probabilidad utilizados en la escuela, o en la enseñanza universitaria no especializada, son los significados intuitivo, clásico, frecuencial, subjetivo y axiomático. Cada uno de estos implican diferencias específicas, no solo en la propia definición de probabilidad, sino también en los conceptos, propiedades y procedimientos que se le relacionan y han surgido para resolver o modelar problemas o fenómenos del mundo real (Batanero, 2005; Batanero y Díaz, 2007; Batanero et al., 2016; Borovcnik y Kapadia, 2014).
En este trabajo nos limitamos a los significados intuitivo, clásico, frecuencial y subjetivo de la probabilidad, debido a su importancia en los currículos actuales de nivel educativo secundaria, citado por los anteriores autores y por Beltrán-Pellicer et al. (2018).
El significado intuitivo, que apareció en la historia antes del estudio mate-mático de la probabilidad (Batanero y Díaz, 2007), se corresponde con las ideas intuitivas que pueden tener los niños pequeños o personas sin formación acerca de los fenómenos aleatorios. No en vano, nuestro lenguaje verbal está lleno de expresiones cualitativas (como los términos imposible, probable, seguro) que permiten indicar nuestro grado de creencia personal sobre la ocurrencia de ciertos acontecimientos.
La primera definición matemática de probabilidad viene asociada al significado clásico, dada por Moivre en 1718 y refinada por Laplace en 1814 como “la proporción del número de casos favorables al número de casos posibles, siempre que todos los resultados sean igualmente probables” (Batanero, 2005; Borovcnik y Kapadia, 2014). Esta definición, válida solo para espacios muestrales con un número finito de sucesos elementales y equiprobables, es además circular, y dio lugar a la regla de Laplace y al cálculo de la probabilidad en situaciones de juegos de azar, donde se suele aplicar el razonamiento combinatorio (Batanero y Borovcnik, 2016; Jones, 2005).
En el significado frecuencial, que se origina a partir de la publicación por Bernoulli de la primera ley de los grandes números, se define la probabilidad como el valor hipotético hacia el cual tiende a estabilizarse la frecuencia relativa de un suceso al repetir el experimento un número grande de veces. Tiene la dificultad de que nunca se llega a calcular el valor verdadero de la probabilidad, sino que solo se logra estimar mediante la frecuencia relativa, y tiene el peligro de generar una confusión entre frecuencia relativa y probabilidad (Batanero, 2005; Borovcnik y Kapadia, 2014). Sin embargo, frente al enfoque clásico, tiene la ventaja de poder aplicarse a experimentos con sucesos no equiprobables.
El significado subjetivo surge a partir del teorema de Bayes, que permite transformar probabilidades a priori, de algunas causas, en probabilidades a posteriori, que incorporan la información de los datos observados. Por ejemplo, permite averiguar la probabilidad de tener cierta enfermedad dados algunos síntomas a partir del conocimiento de la probabilidad de tener esa enfermedad y la probabilidad (a priori) de tener esos síntomas dada esa enfermedad. Por tanto, matemáticos como Finetti o Ramsey conciben la probabilidad como grado de creencia personal (Borovcnik y Kapadia, 2014). Este significado amplía mucho el campo de aplicación, pero no se suele tratar en el currículo hasta que se introduce la probabilidad condicional (Batanero, 2005).
La controversia sobre los diversos significados de la probabilidad se resolvió con la axiomática de Kolmogorov. Al considerar los sucesos como conjuntos, podemos pensar en el espacio muestral como el conjunto total y en los sucesos como subconjuntos de este. De esta manera, la axiomática permite emplear el rigor de la teoría de conjuntos y, al interpretar la probabilidad como una medida, aplicar la teoría de la medida (Batanero y Díaz, 2007; Batanero et al., 2005). Aunque algunos textos de final de la secundaria incorporan los axiomas de Kolmogorov, en general, no es necesario utilizar el significado axiomático en la educación primaria o secundaria, por ser demasiado formal y solo adecuado para quienes siguen estudios universitarios o las matemáticas puras (Batanero et al., 2016).
2.3. Antecedentes sobre análisis de materiales curriculares
La inclusión y tratamiento de la probabilidad desde los primeros niveles educativos se relaciona tanto con su utilidad para la vida diaria como con su papel instrumental en otras disciplinas (Gal, 2005; Jones, 2005). A pesar de esta importancia, no encontramos muchos estudios sobre el tratamiento de los contenidos de probabilidad en el currículo y en los libros de texto y, en general, aquellos encontrados concluyen que predominan los aspectos procedimentales por sobre la comprensión conceptual o el desarrollo de razonamiento probabilístico (Azcárate y Serradó, 2006; Barragués y Guisasola, 2006). Ortiz (2002) estudia los tipos de objetos matemáticos definidos en el EOS, incluidos en los libros de texto de secundaria españoles, y pone de manifiesto la complejidad de la tarea de desarrollo curricular y planificación de las acciones didácticas en este campo. Su análisis revela que los libros analizados muestran una clara presentación de los significados clásico y frecuencial, y que una parte importante también incluye la definición axiomática; sin embargo, el significado subjetivo aparece en pocas ocasiones. Además, una vez introducidos estos significados, las actividades se asocian de forma muy clara al significado clásico (experimentos aleatorios donde se aplica el principio de indiferencia y razonamiento combinatorio) y cuando se plantea la recogida de datos es para comprobar que el resultado coincide con el que se obtiene mediante la regla de Laplace. Esto conduce a que las situaciones que se presentan al alumno estén sesgadas hacia el campo de los juegos de azar, sin mostrar otros contextos y aplicaciones reales. También, muestra la existencia de conflictos semióticos de tipo epistémico, por ejemplo, al estudiar la probabilidad condicional se define el “suceso condicionado”, un concepto que no existe en matemáticas.
Gómez-Torres (2014), en el marco de una investigación sobre la evaluación y el desarrollo del conocimiento matemático para enseñar la probabilidad en futuros profesores de educación primaria, basándose también en el EOS, puso en práctica un método para delimitar cada significado de la probabilidad mediante la descripción de configuraciones epistémicas, donde se desgranan todos los objetos matemáticos que emergen de cada uno de los significados de la probabilidad. De esta manera, explora qué objetos se relacionan con cada significado en el currículo español y en una muestra de libros de texto españoles, lo que permite identificar su representatividad. Esta autora analiza los objetos matemáticos separadamente, uno a uno, sin considerar las configuraciones didácticas en los libros de texto. Este es un punto en que nuestro trabajo aporta información original.
3. MÉTODO
El propósito de esta investigación es analizar la representatividad y articulación de los diferentes significados de la probabilidad en los documentos curriculares peruanos del ciclo VI de la educación secundaria (estudiantes de 12-13 años). Con esa orientación, aplicaremos el análisis de contenido (Krippendorff, 2013) al caso de un texto normativo curricular escolar de Perú y los materiales didácticos en probabilidad que le acompañan. Dicho análisis se apoya en las categorías y herramientas del EOS, en concreto, en las nociones de configuración epistémica y configuración didáctica. De esta forma, la investigación tiene un carácter cualitativo (Fraenkel et al., 2011).
En primer lugar, examinamos la organización del programa curricular de matemática. Se distinguen cuatro bloques: resuelve problemas de cantidad; resuelve problemas de regularidad, equivalencia y cambio; resuelve problemas de forma, movimiento y localización; y resuelve problemas de gestión de datos e incertidumbre. Cada una de estos representa una competencia y está precisado mediante capacidades, descripción de nivel de competencia y desempeños (descripciones más específicas de la competencia) por grado.
Centramos nuestro interés en el bloque de resolución de problemas de incertidumbre (probabilidad) para estudiantes de primer y segundo grado (ciclo VI) de educación secundaria (estudiantes de 12 y 13 años, respectivamente).
En la tabla 1, describimos los desempeños que tratan sobre probabilidad en primer y segundo grado. Nos referiremos a cada uno de estos desempeños por sus abreviaturas (DGx.y). Por ejemplo, DG1.3 es el código abreviado para el tercer desempeño del primer grado, y DG2.1 hace referencia al primer desempeño de segundo grado de educación secundaria.
Tabla 1 Desempeños del ciclo VI de educación secundaria
| Desempeños de primer grado de secundaria | Desempeños de segundo grado de secundaria |
| DG1.1 Determina las condiciones de una situación aleatoria, compara la frecuencia de sus sucesos y representa su probabilidad a través de la regla de Laplace (valor decimal) o representa su probabilidad mediante su frecuencia dada en porcentajes. A partir de este valor, determina si un suceso es más o menos probable que otro. | DG2.1 Determina las condiciones y el espacio muestral de una situación aleatoria, y compara la frecuencia de sus sucesos. Representa la probabilidad de un suceso a través de la regla de Laplace (valor decimal) o representa su probabilidad mediante su frecuencia relativa expresada como decimal o porcentaje. A partir de este valor determina si un suceso es seguro, probable o imposible de suceder. |
| DG1.2 Expresa con diversas representaciones y lenguaje matemático su comprensión sobre (…) el valor de la probabilidad para caracterizar como más o menos probable la ocurrencia de sucesos de una situación aleatoria. | DG2.2 Expresa con diversas representaciones y lenguaje matemático su comprensión sobre (…) el significado del valor de la probabilidad para caracterizar como segura o imposible la ocurrencia de sucesos de una situación aleatoria |
| DG1.3 Lee tablas y gráficos de barras o circulares, así como diversos textos que contengan valores (…), o descripciones de situaciones aleatorias, para comparar e interpretar la información que contienen. A partir de ello, produce nueva información | DG2.3 Lee tablas y gráficos como histogramas, polígonos de frecuencia, así como diversos textos que contengan valores (…) de situaciones aleatorias, para comparar e interpretar la información que contienen y deducir nuevos datos. A partir de ello, produce nueva información. |
| DG1.4 Selecciona y emplea procedimientos para determinar (…) la probabilidad de sucesos simples de una situación aleatoria mediante la regla de Laplace o el cálculo de su frecuencia relativa expresada en porcentaje. Revisa sus procedimientos y resultados. | DG2.4 Selecciona y emplea procedimientos para determinar (…) la probabilidad de sucesos de una situación aleatoria mediante la regla de Laplace o el cálculo de su frecuencia relativa expresada como porcentaje. Revisa sus procedimientos y resultados |
| DG1.5 Plantea afirmaciones o conclusiones sobre (…) la probabilidad de ocurrencia de sucesos. Reconoce errores en sus justificaciones y los corrige. | DG2.5 Plantea afirmaciones o conclusiones sobre (…) la probabilidad de ocurrencia de sucesos en estudio. Las justifica usando la información obtenida, y sus conocimientos estadísticos y probabilísticos. Reconoce errores en sus justificaciones y en las de otros, y los corrige. |
De igual forma, abreviaremos la descripción de nivel de competencia esperado al finalizar el ciclo VI con el código NC6.
Dado que, en la perspectiva del EOS, el significado institucional queda delimitado a partir de la configuración epistémica de objetos, para analizar los desempeños y el nivel de competencia se ha procedido, en primer lugar, a asociar los términos y expresiones según la tipología de objetos (situaciones-problema, lenguajes, procedimientos, argumentos y conceptos-definición), con los significados intuitivo, frecuencial y clásico (no habiéndose encontrado el significado subjetivo; posiblemente debido al nivel escolar, donde aún no se estudia la probabilidad condicional).
En segundo lugar, se seleccionan y analizan los cuadernos de trabajo de matemática de secundaria, facilitados por el Ministerio de Educación: Resolvamos Problemas de primer grado (MINEDU, 2019a) y Resolvamos Problemas de segundo grado (MINEDU, 2019b); cada uno contiene 20 fichas que abordan diferentes temas de matemática. En el cuaderno de trabajo de primer grado se identifican dos fichas (n.º 9 y n.º 13) que abordan la probabilidad, de las cuales se ha examinado la primera por contener la mayor cantidad de situaciones-problemas. En lo que respecta al cuaderno de segundo grado, se identificó una sola ficha (n.º 13), que también es analizada.
Todas las fichas están organizadas en tres secciones: (1) aplicación, (2) comprobación y (3) evaluación de aprendizajes, cada una con un propósito relacionado con los desempeños prescritos en el programa curricular y concretada mediante diferentes situaciones-problemas. Así, la sección de aplicación introduce una situación-problema siguiendo los pasos resolutivos de Polya (1945) y sus enunciados específicos, la de comprobación expone tres situaciones-problemas con sus respectivos procedimientos de resolución predeterminadas, y la de evaluación de aprendizajes propone 10 situaciones-problemas que el estudiante debe resolver.
Para el análisis didáctico, se ha considerado cada sección de la ficha como una unidad o configuración didáctica. Las configuraciones 1, 2 y 3 corresponden a la ficha n.º 9 de primer grado y la configuración 4, 5 y 6 a la ficha n.º 13 de segundo grado. Así mismo, en cada configuración didáctica se describen las prácticas y objetos matemáticos que intervienen, así como los conflictos semióticos potenciales que se van manifestando.
4. ANÁLISIS DEL PROGRAMA CURRICULAR DE EDUCACIÓN SECUNDARIA EN PROBABILIDAD
En esta sección se muestran los términos y expresiones incluidos en el programa curricular que hacen referencia a los diferentes significados de la probabilidad, así como los objetos matemáticos relacionados con los mismos.
El currículo señala que el estudiante, al finalizar el ciclo VI de educación secundaria, debe haber adquirido la siguiente competencia:
Expresa la probabilidad de un evento aleatorio como decimal o fracción, así como su espacio muestral; e interpreta que un suceso seguro, probable e imposible se asocia a los valores entre 0 y 1. Hace predicciones sobre la ocurrencia de eventos y las justifica (NC6) (MINEDU, 2016, p. 172).
Por tanto, los registros lingüísticos en los que se espera que los estudiantes se desenvuelvan son el verbal y el simbólico-numérico (representación fraccionaria, decimal y enteros). La competencia del NC6 implica los econcptos-definiciones: evento o situación aleatoria, probabilidad, espacio muestral, suceso, suceso seguro, suceso probable, suceso imposible, decimal y fracción. También, aparecen involucradas proposiciones como “el suceso seguro siempre ocurre”, “el suceso imposible nunca se verifica” y “la probabilidad de un suceso se asocia a un número entre 0 y 1”. Para justificar las proposiciones esperadas del NC6, se pide que el estudiante emplee argumentos que apoyen en demostrar la ocurrencia de eventos, así como la asignación de valores entre 0 y 1 a un suceso seguro, probable e imposible.
En la descripción del NC6 no se identifican claramente los significados de la probabilidad por medio de objetos asimilables a cada uno de ellos, por lo cual podría relacionarse tanto con el significado clásico como con el frecuencial, teniendo algunos elementos del intuitivo (valoración cualitativa del grado de probabilidad, predicciones). Como veremos a continuación, la delimitación de los significados de la probabilidad en el programa curricular se consigue con el análisis de los desempeños de primer y segundo grado de educación secundaria, puesto que son mucho más específicos que las descripciones de los niveles competenciales.
4.1 Desempeños de primer y segundo grado de educación secundaria
En el currículo escolar peruano los desempeños son “descripciones específicas de lo que hacen los estudiantes” (MINEDU, 2016, p. 193) respecto al nivel de desarrollo de la competencia (NC6) y, en algunas ocasiones, son iguales en primer y segundo grado, debido a que requieren mayor tiempo para su desarrollo (MINEDU, 2016). En tal sentido, como se describe en la sección de metodología, se han identificado y codificado cinco desempeños tanto para primer grado (DG1.1 a DG1.5) como segundo grado (DG2.1 a DG2.5). Entre ellos, los desempeños DG1.1, DG1.4, DG2.1 y DG2.4 explicitan términos y expresiones que hacen referencia al significado clásico y frecuencial, como es el uso de la regla de Laplace y el cálculo de frecuencias o frecuencia relativa dentro de sus procedimientos. Mientras que los desempeños DG1.2, DG1.3 y DG1.5, así como DG2.2, DG2.3 y DG2.5, no determinan claramente un significado concreto de la probabilidad. Esta falta de precisión puede conllevar su orientación al significado clásico y significado frecuencial, incluso al intuitivo, observado en indicios de valoración cualitativa de la probabilidad.
En la tabla 2 se desglosan los objetos matemáticos característicos de los significados de la probabilidad (Batanero, 2005; Beltrán-Pellicer et al., 2018; Vásquez y Alsina, 2015) mostrando en qué caso han sido identificados en los desempeños de cada grado.
Tabla 2 Objetos matemáticos relacionados a los significados de la probabilidad y los desempeños por grado
| Objetos matemáticos | Significados | Desempeños | |||
|---|---|---|---|---|---|
| Clásico | Frecuencial | Intuitivo | 1° | 2° | |
| Situaciones-problema | |||||
| Reconocer las condiciones que definen una situación aleatoria | X | X | X | X | X |
| Expresar el valor (decimal o porcentajes) de la probabilidad como más o menos probable | X | X | X | ||
| Determinar el espacio muestral | X | X | X | X | |
| Expresar el valor (decimal o porcentajes) de la probabilidad como seguro, probable o imposible | X | X | X | ||
| Determinar la probabilidad de sucesos con regla de Laplace o cálculo de su frecuencia relativa | X | X | X | X | |
| Interpretar información de diversos textos con valores o descripciones de situaciones aleatorias | X | X | X | X | X |
| Plantear afirmaciones o conclusiones sobre la probabilidad de ocurrencia de sucesos | X | X | X | X | X |
| Lenguajes | |||||
| Verbal | X | X | X | X | X |
| Simbólico - numérico | X | X | X | X | X |
| Gráfico | X | X | X | X | X |
| Tabular | X | X | X | X | |
| Conceptos-definición | |||||
| Situación aleatoria | X | X | X | X | X |
| Espacio muestral | X | X | X | X | |
| Sucesos, sucesos simples | X | X | X | X | X |
| Suceso más o menos probable | X | X | X | X | |
| Suceso seguro, probable e imposible | X | X | X | X | |
| Probabilidad | X | X | X | X | X |
| Frecuencia, frecuencia relativa | X | X | X | ||
| Procedimientos | |||||
| Identificación de las condiciones de una situación aleatoria | X | X | X | X | X |
| Comparación de la probabilidad expresada en decimales o porcentajes | X | X | X | X | |
| Enumeración de sucesos elementales | X | X | X | X | |
| Aplicación de la regla de Laplace | X | X | X | ||
| Representación simbólica o gráfica | X | X | X | X | X |
| Lectura de tablas, gráficos y textos con situaciones aleatorias | X | X | X | X | X |
| Cálculo de la frecuencia relativa y porcentaje | X | X | X | ||
| Revisar procedimientos | X | X | X | X | X |
| Extraer conclusiones y corregir errores | X | X | X | X | X |
| Proposiciones | |||||
| Regla de Laplace | X | X | X | ||
| La frecuencia relativa de un suceso varía entre 0 y 1 | X | X | X | ||
| La probabilidad de un suceso es un valor calculable | X | X | X | X | |
| Argumentos | |||||
| Plantear afirmaciones y extraer conclusiones | X | X | X | X | X |
| Reconocer errores en sus justificaciones | X | X | X | X | X |
| Deducción a partir de datos | X | X | X | X | |
Casi todos los desempeños pueden asociarse tanto al enfoque clásico como al frecuencial, salvo aquellos que mencionan explícitamente la regla de Laplace. En lo que respecta al significado frecuencial, se incluyen procedimientos de naturaleza estadística, pero no procedimientos de experimentación y simulación. El significado intuitivo está muy presente, ya que en casi todos los objetos se alude a la probabilidad como grado de creencia personal. Finalmente, cabe observar que no se hace mención de revisar estos grados de creencia con base a la nueva información disponible, por lo que no aparece representado el significado subjetivo de la probabilidad.
5. Análisis de las fichas del cuaderno de trabajo “Resolvamos problemas”
El análisis que realizamos a continuación sobre los materiales curriculares proporcionados para cada grado, y que además se llevan al trabajo de aula, permitirá determinar el tratamiento efectivo de los desempeños con relación a los significados de la probabilidad.
5.1 Material curricular de primer grado de educación secundaria
La ficha dedicada a probabilidad (ficha n.º 9) consta de tres secciones: aplicación, comprobación y evaluación. De cada una de estas secciones, emerge una configuración didáctica, como mostramos a continuación:
Configuración didáctica 1 (sección de aplicación)
En esta configuración se contemplan tres desempeños: expresar el valor de la probabilidad como más o menos probable (DG1.2), aplicar la regla de Laplace (DG1.4) y justificar con ejemplos la probabilidad de ocurrencia de sucesos (DG1.5).
Prácticas y objetos matemáticos
Introduce una situación-problema vinculada al significado clásico y contextualizada al juego de la ruleta, donde se debe calcular la probabilidad de ciertos sucesos (premio, descuento o agradecimiento). Si bien la ruleta es un dispositivo que permitiría abordar el significado frecuencial considerando sucesos elementales no equiprobables, al estar dividida en sectores de igual amplitud (figura 1), la situación se relaciona con el significado clásico.
Conflictos semióticos potenciales
- A pesar de que en la ruleta se indica claramente qué sectores otorgan premio, se observan también iconos (caracoles y estrellas) que no están directamente relacionados con los dos enunciados del problema. Esto puede generar confusión en la interpretación de datos y en la enumeración correcta de todos los sucesos elementales (Bryant y Nunes, 2012).
- En el texto de la actividad (ver figura 1) se utilizan términos relacionados con situaciones aleatorias como resultados posibles y favorables, sucesos y probabilidad. Si la secuencia global no lo tiene en cuenta, podrían darse por supuestos estos objetos y provocar un conflicto de interpretación.
- Podría haber una confusión del espacio muestral, considerando solo dos casos equiprobables (aceptar y perder), pues el primero tiene de hecho probabilidad 1/3. Si el profesor no reflexiona sobre la no equiprobabilidad del suceso compuesto (aunque los sucesos elementales sean equiprobables) y no articula esta con otras situaciones donde no tenga sentido esta suposición, estaría fomentando el sesgo de equiprobabilidad y la creencia de que sucesos elementales de cualquier experimento son equiprobables (Lecoutre, 1992).
Configuración didáctica 2 (sección de comprobación)
Esta configuración contempla dos desempeños: determinar las condiciones de una situación aleatoria, aplicar la regla de Laplace, determinar si un suceso es más o menos probable (DG1.2) y justificar con ejemplos la probabilidad de ocurrencia de sucesos (DG1.5). Se desarrollan mediante tres situaciones, A, B y C, que giran en torno a la aplicación de la regla de Laplace.
Prácticas y objetos matemáticos
La situación-problema A, contextualizada en un juego de dados, pide determinar si los sucesos del enunciado resultan ser seguros, imposibles o probables. Dado que en el enunciado no se pide al estudiante un valor numérico de la probabilidad, sino una asignación cualitativa de la ocurrencia de los sucesos asociado a expresiones verbales (imposible, seguro o probable), podría abordarse desde el significado intuitivo. No obstante, como hay una cierta cuantificación latente y el espacio muestral consta de un número finito de sucesos elementales y equiprobables, la situación aleatoria corresponde al significado clásico.
La situación-problema B, cuyo contexto es el lanzamiento simultáneo de dos dados, requiere determinar el espacio muestral, identificar la suma más probable y calcular la probabilidad de la suma más probable. Como se trata de asignar un valor numérico usando la regla de Laplace, la situación se relaciona directamente con el significado clásico.
La situación-problema C, planteada en un contexto biológico, pide calcular la probabilidad de que mellizos sean de distinto sexo. El espacio muestral consta de un número finito de sucesos y el valor numérico de la probabilidad se obtiene mediante la regla de Laplace, por lo que la situación corresponde al significado clásico.
Conflictos semióticos potenciales
- En la situación A, se define espacio muestral como el conjunto de todos los posibles resultados de un experimento aleatorio. “Resultado” es un término poco preciso que alude a cualquier suceso que pueda ocurrir en el experimento, por lo que es más adecuado hablar de sucesos elementales (Serradó, Cardeñoso y Azcárate, 2005). También se emplea, al enunciar la regla de Laplace, el término “caso”, cuando se podría haber unificado al hablar de sucesos elementales. Este uso diverso de términos puede conducir a conflictos semióticos a la hora de asignar el significado (Gómez-Torres, 2014; Serradó et al., 2005). Otro conflicto se produce al expresar la probabilidad como porcentaje también puede haber un conflicto, pues se indica “Para expresar la probabilidad en porcentajes, multiplicamos por 100 %”, lo cual es un procedimiento carente de significado.
- En la situación B, se utiliza la tabla de doble entrada sin abordar por qué o en qué situación aleatoria es necesario o pertinente su uso.
- En la situación C, no queda claro cuál es el método, la forma de componer cada elemento del espacio muestral, ni si el orden de los sexos de los mellizos importa. Sería conveniente justificar el uso de la enumeración sistemática, que consiste en formar la lista de los sucesos elementales organizados en grupos.
- En la situación de los dos dados, puede ocurrir que no se tenga en cuenta el orden y se construya un espacio muestral formado por 21 sucesos elementales, en lugar de 36.
En las tres situaciones del bloque de comprobación se aplica la regla de Laplace, pero se omite la justificación de las condiciones de su uso; lo mismo sucede con la escala de la probabilidad, es decir, hay ausencia de argumentación y justificación en los procedimientos de resolución. Además, se suponen conocidos los conceptos de situación aleatoria, casos favorables, casos posibles, tipos de suceso, suceso simple, experimento compuesto, suceso seguro, suceso imposible, probabilidad, métodos combinatorios, fracciones y porcentajes. Es posible que sea debido a que se consideran conceptos básicos y argumentaciones triviales. De hecho, experimento aleatorio, casos favorables, posibles, suceso seguro e imposible son conceptos que se espera que los estudiantes dominen al acabar el ciclo V (MINEDU, 2016, p. 171). Por último, al tratarse de una situación desde el significado clásico, al igual que se comentó en la configuración didáctica 1, tenemos el conflicto potencial asociado a la equiprobabilidad.
Configuración didáctica 3 (sección de evaluación)
Esta sección pretende lograr cuatro desempeños: determinar las condiciones de una situación aleatoria, aplicar la regla de Laplace y determinar si un suceso es más o menos probable que otro (DG1.1); expresar el valor de la probabilidad como más o menos probable (DG1.2); determinar la probabilidad de sucesos simples con la regla de Laplace (DG1.4); y justificar mediante ejemplos la probabilidad de la ocurrencia de sucesos (DG1.5). Para tales objetivos, se proponen diez situaciones-problemas, de las cuales nueve (1, 2, 4, 5, 6, 7, 8, 9 y 10) se plantean en el contexto de juegos de azar relacionados al significado clásico, mientras que en la situación aleatoria 3 subyace el significado frecuencial.
Prácticas y objetos matemáticos
Del grupo de situaciones-problemas vinculadas al significado clásico, en seis (1, 2, 5, 6, 7 y 10) se requiere comparar y valorar los resultados de las probabilidades de los sucesos simples. En las situaciones-problemas 4, 8 y 9 se pide calcular la probabilidad de sucesos compuestos, lo que requiere el uso de estrategias combinatorias. Por otro lado, en la situación-problema 3, de significado frecuencial y planteada en el contexto de las disciplinas deportivas que practican los estudiantes, se pide calcular la probabilidad del suceso complementario (no practican básquet) a partir de los datos expuestos en un gráfico de sector circular.
Conflictos semióticos potenciales
- En la situación-problema 3 no se incluye el título en el gráfico de sector circular. Como señalan Arteaga y Díaz-Levicoy (2016) o Vidal-Henry et al. (2020) la omisión de títulos en los gráficos estadísticos puede causar conflicto en la interpretación de la información.
- Para resolver las situaciones-problemas de esta sección, se suponen conocidos los conceptos de situación aleatoria simple y compuesta.
- Al igual que en la situación 2, puede haber conflictos al no tener en cuenta el orden en la formación de los sucesos elementales del experimento compuesto.
En la tabla 3, expresamos los objetos matemáticos mencionados y su intervención en cada una de las configuraciones referidas.
Tabla 3 Objetos matemáticos identificados en las configuraciones 1, 2 y 3
| Objetos matemáticos | Configuración didáctica | ||
|---|---|---|---|
| 1 | 2 | 3 | |
| Lenguajes | |||
| Expresión verbal | X | X | X |
| Expresiones simbólico-numéricos (desigualdad, enteros, decimales, fracciones, porcentajes) | X | X | X |
| Gráficos (diagrama de árbol y sector circular) | X | X | |
| Tabulares (tabla de doble entrada y de frecuencias) | X | X | |
| Conceptos-definiciones | |||
| Situación aleatoria, experimento aleatorio simple y compuesto | X | X | X |
| Sucesos; suceso simple y compuesto; suceso más o menos probable; suceso seguro e imposible | X | X | X |
| Casos posibles y favorables | X | X | X |
| Espacio muestral | X | X | X |
| Probabilidad | X | X | X |
| Frecuencia, frecuencia relativa y absoluta, población | X | ||
| Procedimientos | |||
| Lectura y análisis de textos y gráficos de la situación aleatoria | X | X | X |
| Enumeración de sucesos elementales | X | X | X |
| Construir tablas o diagramas de árbol para contar casos posibles y favorables | X | X | |
| Diferenciación de casos posibles y favorables | X | X | X |
| Aplicación de la regla de Laplace | X | X | X |
| Comparación del valor de la probabilidad | X | X | X |
| Ordenar el valor de la probabilidad para caracterizar como más o menos probable y como seguro, probable o imposible de ocurrir | X | X | X |
| Elaboración de una tabla y cálculo de frecuencias relativas | X | ||
| Procedimiento combinatorio | X | X | |
| Proposiciones | |||
| El espacio muestral es finito y numerable | X | X | |
| Equiprobabilidad | X | X | X |
| Regla de Laplace | X | X | |
| La probabilidad es un valor entre 0 y 1 | X | X | |
| La frecuencia relativa de un suceso varía entre 0 y 1 | X | ||
| Probabilidad del suceso compuesto como suma de la probabilidad de los simples | X | X | |
| El número de sucesos elementales del experimento compuesto es el producto del número de elementos de los experimentos simples que lo componen | X | ||
| Argumentos | |||
| Uso de gráficas y ejemplos | X | ||
Teniendo en cuenta que la mayoría de las situaciones-problemas incluidas en la ficha 9 corresponden al significado clásico (solo una está vinculada al significado frecuencial), no es extraño que la mayoría de los objetos recogidos en la tabla 3 correspondan en las tres configuraciones a dicho enfoque. No existen diferencias significativas entre las tres configuraciones, salvo en lo relativo a las proposiciones que apenas se identifican en la configuración de evaluación. También es significativa la ausencia de argumentos (solo en la configuración de comprobación y únicamente en base a gráficas o ejemplos).
5.2 Material curricular de segundo grado de educación secundaria
En la ficha n.º 13 se exponen catorce situaciones agrupadas en tres secciones: aplicación, comprobación y evaluación. A continuación, analizamos estas configuraciones.
Configuración didáctica 4 (sección de aplicación)
En esta sección se desarrollan dos desempeños: determinar la probabilidad de sucesos mediante la regla de Laplace (DG2.4) y expresar con lenguaje matemático el valor de la probabilidad (DG2.2).
Prácticas y objetos matemáticos
Para introducir el significado frecuencial, la sección comienza con la situación-problema incluida en la figura 2.

Figura 2 Situación introductoria en la sección de aplicación de la Ficha 13 de primer grado. Fuente: MINEDU, 2019b, p. 171.
En ella se pide determinar a partir de los datos de una tabla el número de pasajeros que puede esperar la empresa. Además, solicita imaginar 10 fines de semana para estimar la demanda de pasajeros por escenario y calcular la frecuencia absoluta de los fines de semana. La situación no es suficientemente representativa del significado frecuencial, puesto que para ello se debieran dar datos de sucesivas repeticiones de un experimento, donde se pudiese observar la convergencia.
Conflictos semióticos potenciales
- El propósito de esta sección es la aplicación de la regla de Laplace, tal y como indica en el encabezado:
- Empleamos procedimientos para determinar la probabilidad de sucesos de una situación aleatoria mediante la regla de Laplace. Asimismo, expresamos con lenguaje matemático nuestra comprensión sobre el valor de la probabilidad en una situación aleatoria (MINEDU, 2019b, p. 171).
- Sin embargo, la situación-problema planteada no lo permite, dado que los sucesos (cada uno de los escenarios) no son equiprobables (figura 2).
- La tabla adjunta a la situación aleatoria no lleva un título, hecho que puede confundir a la hora de la interpretación de la información.
- En el enunciado del problema (ver figura 2) no queda claro si se trata de cal-cular el número de pasajeros por cada escenario o en el total de escenarios.
- Para resolver la situación-problema, se suponen conocidos los términos estimación, probabilidad, frecuencia absoluta y relativa y media aritmética. Si el docente no ha trabajado con anterioridad los conceptos-definiciones mencionados, es posible que requiera introducirlos en la resolución del problema.
Configuración didáctica 5 (sección de comprobación)
En esta configuración se persiguen dos desempeños: determinar el espacio muestral de una situación aleatoria y calcular probabilidades mediante la regla de Laplace (DG2.1); justificar con conocimientos estadísticos la probabilidad de ocurrencia (DG2.5). Para esto, expone tres situaciones, A, B y C, que buscan la aplicación de la regla de Laplace.
Prácticas y objetos matemáticos
La situación-problema A que trata sobre el lanzamiento de dos monedas y un dado, pide calcular la probabilidad de obtener solo una cara y un número impar. Para responder al enunciado, en la ficha se predefine unos pasos de resolución que involucran objetos matemáticos relacionados al significado clásico de la probabilidad, mientras que la situación-problema B incorpora una situación en la que sería posible introducir elementos del significado frecuencial, ya que presenta los datos recogidos en una encuesta demográfica. Asimismo, pide calcular la probabilidad de tres sucesos (practicar natación, practicar algún deporte y practicar vóley) a partir de la información dada en un gráfico de barras (ver Figura 3). Sin embargo, la resolución que se muestra se realiza exclusivamente desde el significado clásico, puesto que no hay ninguna actividad relacionada con la repetición de un experimento y estimación de la probabilidad mediante la frecuencia relativa.

Figura 3 Gráfico de barras en una actividad de la segunda sección de la Ficha 13 de segundo grado. Fuente: MINEDU, 2019b, p. 171.
La situación-problema C corresponde al contexto geométrico, en el que se debe calcular la probabilidad de la caída del dardo en la zona X de la figura 4.
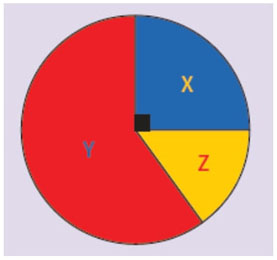
Figura 4 Diana propuesta en una actividad de la segunda sección de la Ficha 13 de segundo grado. Fuente: MINEDU, 2019b, p. 177.
En esta situación, al estudiante se le reta a señalar si el procedimiento establecido en la ficha es correcto o incorrecto, con su respectiva justificación. Si el estudiante identifica el error, tiene la posibilidad de proponer que la situación aleatoria puede ser abordada desde el significado frecuencial, realizando el experimento y recogiendo datos, ya que los sucesos elementales no son equiprobables. En la ficha se sugiere que esta situación se resuelve dividiendo el círculo en sectores apropiados, posiblemente para poder aplicar la regla de Laplace. No obstante, es una situación que también puede ser abordada de forma teórica a partir de consideraciones geométricas, teniendo en cuenta la relación entre las medidas de las áreas.
Conflictos semióticos potenciales
- En el propósito de la situación A se indica “Determinamos el espacio muestral de una situación aleatoria mediante la regla de Laplace (valor decimal) y a partir de este valor identificamos si un suceso es seguro, probable o imposible” (MINEDU, 2019b, p. 174). Esto es confuso, pues la regla de Laplace no se utiliza para determinar el espacio muestral, sino para calcular la probabilidad de sucesos. Cuando se utiliza, se emplea un simbolismo abreviado n(A)/n(Ω) que puede resultar innecesario e inadecuado en esta etapa escolar.
- En la situación A se utiliza el diagrama de árbol sin justificar en qué casos de experimentos aleatorios es conveniente su uso. Convendría aclarar que el conjunto de todos los casos posibles listados, son generados mediante un proceso combinatorio a partir del producto de los sucesos elementales de dos experimentos aleatorios simples (Bryant y Nunes, 2012).
- En la situación B se omite el título del gráfico de barras, lo que nuevamente puede causar conflictos en la lectura e interpretación de la información expuesta (Díaz-Levicoy y Arteaga, 2017).
- En el procedimiento de resolución que se describe en B, se presenta algorítmicamente el uso de la regla de Laplace obviando el hecho de que los datos se han obtenido mediante la repetición del mismo experimento cierto número de veces (aplicación de la encuesta a cada estudiante) y que se presenta un diagrama de barras que se corresponde con el diagrama de frecuencias. En la resolución del cuadernillo, el espacio muestral ya no es “practica vóley”, “practica fútbol” y “practica básquet”, sino que está formado por todos y cada uno de los estudiantes. En caso de hacerlo así, sería necesario indicar que estamos considerando como sucesos elementales “estudiante 1 que practica básquet”, “estudiante 2 que practica básquet”, etc.
- En esta configuración se suponen conocidos algunos conceptos y procedimientos, que pueden ser desconocidos para el estudiante, por ejemplo, los diagramas en árbol, la probabilidad en el contexto geométrico y el cálculo de áreas de sectores, que no están contemplados en el currículo de segundo grado.
- Respecto a la regla de Laplace, al igual que en las configuraciones anteriores, se puede producir un conflicto si no se exige una reflexión antes de asumir el modelo de equiprobabilidad.
Configuración didáctica 6 (sección de evaluación)
En esta configuración se persigue: determinar el espacio muestral de una situación mediante la regla de Laplace e identificar si el suceso es seguro, probable o imposible (DG2.1); expresar con lenguaje matemático el valor de la probabilidad de una situación aleatoria (DG2.2); determinar la probabilidad de sucesos mediante la regla de Laplace (DG2.4); y justificar con conocimientos estadísticos la probabilidad de ocurrencia de sucesos en estudio y corregir errores si los hubiera (DG2.5).
Prácticas y objetos matemáticos
Se proponen diez situaciones-problemas, de las cuales nueve responden al significado clásico y solo una (n.º 7) a una primera aproximación al significado frecuencial. Del grupo de situaciones-problemas asociadas al significado clásico planteadas en el contexto de juegos de azar, cuatro (1, 3, 4 y 9) involucran la comparación de las probabilidades de los sucesos de una situación aleatoria simple, mientras que las situaciones-problemas 2, 5, 6 y 8 implican el cálculo de la probabilidad de sucesos en situaciones aleatorias compuestas. El contexto de la situación-problema 10 es la lectura de una revista entre hombres y mujeres que trabajan en una empresa, y trata de una situación aleatoria compuesta que involucra el cálculo de la probabilidad a partir de la dependencia de sucesos. La situación-problema 7, asociada al significado frecuencial y planteada en el contexto de uso de las redes sociales, requiere el cálculo de la frecuencia relativa y porcentaje a partir de la información disponible en una tabla de frecuencias. En ambos casos, se introducen elementos que se necesitan para una introducción posterior de un enfoque frecuencial completo.
Conflictos semióticos potenciales
- En la situación 7 se omite el título de la tabla de frecuencias, lo que puede causar conflictos en la interpretación de la información.
- Es posible que el estudiante de segundo grado de educación secundaria tenga conflictos durante el proceso de resolución de las situaciones aleatorias 6, 8 y 9, dado que el tratamiento de la probabilidad con sucesos independientes y dependientes no está considerado en los desempeños de segundo grado, ni ha sido tratada en las secciones anteriores de la ficha.
En la tabla 4, expresamos los objetos matemáticos mencionados y su intervención en cada una de las configuraciones referidas.
Tabla 4 Objetos matemáticos identificados en la configuración 4, 5 y 6
| Objetos matemáticos | Configuración didáctica | ||
|---|---|---|---|
| 4 | 5 | 6 | |
| Lenguajes | |||
| Expresión verbal | X | X | X |
| Expresiones simbólico-numéricos (desigualdad, enteros, decimales, fracciones, porcentajes) | X | X | X |
| Gráficos (diagrama de árbol y sector circular) | X | X | |
| Tabulares (tabla de doble entrada y de frecuencias) | X | X | |
| Conceptos-definiciones | |||
| Situación aleatoria, experimento aleatorio simple y compuesto | X | X | X |
| Sucesos, sucesos independientes y dependientes | X | X | X |
| Resultados/Casos posibles y favorables | X | X | |
| Espacio muestral | X | X | X |
| Probabilidad | X | X | X |
| Frecuencia, frecuencia relativa y absoluta, población, estimación | X | X | |
| Sector circular | X | ||
| Procedimientos | |||
| Lectura y análisis de textos y gráficos de la situación aleatoria | X | X | X |
| Enumeración de sucesos elementales | X | X | |
| Construir tablas o diagramas de árbol para contar casos posibles y favorables | X | X | |
| Diferenciación de casos posibles y favorables | X | X | |
| Aplicación de la regla de Laplace | X | X | |
| Comparación del valor de la probabilidad | X | X | |
| Elaboración de una tabla y cálculo de frecuencias relativas | X | X | |
| Proposiciones | |||
| El espacio muestral es finito y numerable | X | X | |
| Equiprobabilidad | X | X | |
| Regla de Laplace | X | X | |
| La probabilidad es un valor entre 0 y 1 | X | X | |
| La frecuencia relativa de un suceso varía entre 0 y 1 | X | X | |
| Argumentos | |||
| Ejemplos | X | ||
Se observa gran riqueza en los registros lingüísticos en las tres configuraciones, el predominio de los objetos referidos al significado clásico frente al frecuencial y una casi ausencia de procedimientos y proposiciones en la configuración 4 respecto a la 5 y 6. Además, los únicos argumentos encontrados en la configuración 5 se basan en ejemplos.
6. CONCLUSIONES
El análisis conjunto del programa curricular y las fichas de trabajo, con las herramientas del EOS, nos ha permitido concluir la preferencia del significado clásico en detrimento del significado frecuencial e intuitivo de la probabilidad. Este resultado coincide con las investigaciones previas de análisis de texto en probabilidad (Gómez-Torres, 2014; Sánchez, 2009; Serradó et al., 2005; Vásquez y Alsina, 2015) y puede explicarse por la complejidad que tiene una introducción completa al significado frecuencial, pues implicaría la organización de experimentos y recogida sucesiva de datos para observar la convergencia de la frecuencia relativa a la probabilidad; para esto, consideramos como una alternativa, la simulación computacional y el uso de recursos disponibles de Internet.
Al examinar el programa curricular, se evidenció mayor representatividad de objetos matemáticos relacionados a los significados clásico y frecuencial sobre el intuitivo, aun cuando la descripción de NC6 y los desempeños de ambos grados no explicitaban su relación con algún significado de la probabilidad. Esto invita a pensar que se tiene una visión predeterminada de la probabilidad desde el enfoque clásico y frecuencial que obvia la conexión con el intuitivo. Para complementar este análisis y determinar el tratamiento efectivo de los desempeños con relación a los significados de la probabilidad, se tomó la decisión de examinar los materiales curriculares que proponen actividades de probabilidad.
Las actividades del material curricular se dividieron en seis configuraciones didácticas, en las que se identificaron las prácticas y objetos matemáticos que permiten identificar el significado de la probabilidad con el que cada una se vincula, así como los conflictos semióticos potenciales. De las catorce situaciones-problemas expuestas en la ficha 9 de primer grado, trece corresponde al significado clásico y solo en una subyace el significado frecuencial; mientras que, en la ficha 13 de segundo grado, de las catorce situaciones-problemas, once están relacionadas al significado clásico, dos al significado frecuencial y una contempla criterios geométricos en probabilidad. En las configuraciones se suponen conocidos los conceptos-definiciones de situación aleatoria, espacio muestral, sucesos, suceso simple, suceso seguro, probable e imposible, probabilidad, frecuencia y frecuencia relativa, que además están predeterminados en el programa curricular. Por otro lado, las nociones de situación aleatoria simple y compuesta, equiprobabilidad y sucesos dependientes, o contenidos como tablas de doble entrada, diagramas de árbol, la regla de la multiplicación, criterios geométricos en probabilidad, no están contemplados en el programa curricular para ciclo VI y se suponen conocidos. Podría ocurrir, por ejemplo, que al no explicitar cómo justificar las condiciones de equiprobabilidad que tiene que cumplir cierto experimento aleatorio se incurra con mayor facilidad en el sesgo de equiprobabilidad, o que, al no trabajar las tablas de doble entrada, no se desarrolle la competencia necesaria para interpretarlas. No trabajar con experimentos aleatorios compuestos y su representación en tablas de doble entrada puede ocasionar que los estudiantes traten los experimentos compuestos y calculen algunas probabilidades conjuntas de manera imprecisa o errónea, sin considerar la dependencia o independencia de los sucesos. Estas y otras dificultades pueden soslayarse planificando un andamiaje adecuado en un entorno enfocado hacia la resolución de problemas.
El análisis también nos ha permitido identificar conflictos semióticos potenciales, en particular, se observa un uso diverso y poco preciso de términos y expresiones que definen el significado de espacio muestral y sucesos y una ausencia de distinción de los conceptos-definiciones de suceso elemental y compuesto, así como experimento simple y compuesto. No se clarifican las condiciones de uso de la regla de Laplace, de la escala de la probabilidad, ni de los diferentes tipos de representaciones y métodos combinatorios que facilitan la enumeración del espacio muestral en experimentos compuestos; e incluso se observa una aplicación inadecuada de la regla de Laplace cuando las situaciones-problemas no lo permiten, ya que los sucesos elementales no son equiprobables, hecho que fomenta la aparición del sesgo de la equiprobabilidad. Además, no se introducen situaciones-problemas que den sentido al significado frecuencial, permitiendo observar la convergencia, y tan solo se reducen al cálculo de la frecuencia relativa y porcentual a partir de un gráfico o tabla estadística que recogen las frecuencias absolutas. No se pretende experimentación, ni simulación por parte de los estudiantes, hecho que puede generar conflictos de comprensión del significado frecuencial y estabilidad de frecuencias relativas (Serradó et al., 2005).
Teniendo en cuenta los resultados de nuestra investigación y las habituales recomendaciones surgidas en el área de la didáctica de la matemática sobre la enseñanza y aprendizaje de la probabilidad, el profesor que recurra al programa curricular y las fichas de trabajo debería considerar: replantear las actividades propuestas en las fichas de trabajo y conectarlas con el programa curricular; aclarar los conceptos que no han sido trabajados con anterioridad para evitar conflictos semióticos potenciales durante el desarrollo de la ficha de trabajo; desarrollar la competencia sobre el uso de los diferentes tipos de representaciones; contemplar el aprendizaje de métodos combinatorios (tabla de doble entrada, esquemas, enumeración sistemática, diagrama de árbol) que facilitan la enumeración del espacio muestral de experimentos compuestos (no previstos en la normativa curricular); y finalmente, plantear suficientes experiencias físicas con fenómenos aleatorios, simulaciones informáticas y actividades desde el enfoque frecuencial, con interés en sí mismas.
Consideramos que la realización del análisis ontosemiótico de materiales curriculares debería ser una competencia del profesor de matemáticas como parte de una capacidad más general de planificación de lecciones. Por ello es un tema de investigación abierto el diseño e implementación de intervenciones formativas específicas para capacitar a los futuros docentes en el análisis crítico de materiales curriculares (programas, libros de texto, cuadernos para el estudiante) de forma que la gestión de aula cubra los conflictos potenciales.











 nueva página del texto (beta)
nueva página del texto (beta)




