1. ANTECEDENTES
La investigación sobre la introducción de ideas algebraicas en los currículos de educación básica (estudiantes de 6 a 12 años), ha sido por más de dos décadas uno de los principales ejes de análisis para la comunidad educativa internacional. Lo anterior, surgió como una medida que buscaba subsanar lo que, a finales del siglo XX, un gran número de estudios revelaron sobre las dificultades involucradas cuando los estudiantes (12 - 15 años) debían pasar de una forma aritmética a una forma algebraica de razonamiento (e.g., Kieran, 1992; Linchevski, 1995; Rojano y Sutherland, 2001; Wagner y Kieran, 1989). Este movimiento, conocido actualmente como Early Algebra -o álgebra temprana-, tiene por objetivo introducir ideas algebraicas en el currículo escolar elemental, además de construir una base que permita el acceso de los estudiantes a conceptos algebraicos más avanzados en los cursos siguientes (Cai y Knuth, 2011; Carraher y Schliemann, 2007; Kieran et al., 2016).
A partir del evento Algebra Initiative Colloquium (Lacampagne et al., 1995), los estándares para la educación matemática del National Council of Teachers of Mathematics (NCTM, 2000) y los Common Core State Standards (CCSSI, 2010), han incluido temas y recomendaciones para fomentar la inclusión del álgebra desde los primeros niveles educativos (Carraher y Schliemann, 2019). En el año 2000, Kaput sugirió promover el álgebra como facilitadora -más que como inhibidora- de una mejor comprensión de las matemáticas, en una propuesta denominada algebra for all, que tiene como finalidad la algebrización del currículo elemental.
En el marco del álgebra temprana existe un gran número de investigaciones basadas en el análisis del currículo, las cuales evidencian las formas en que son introducidas algunas nociones clave tales como relaciones funcionales, generalización de patrones; además, relacionan el desarrollo del razonamiento algebraico a partir del trabajo con algunas nociones de la aritmética (Aké y Godino, 2018; Cai, 2004; Castro et al., 2017; Fong, 2004; Lew, 2004; NCTM, 2000). Por ejemplo, Watanabe (2008), señala que, en Japón, “el estudio del álgebra en la escuela primaria pretende no sólo desarrollar competencia algebraica sino también promover una comprensión más profunda de otros contenidos en el currículo de matemáticas” (p. 192); para ello, dividen el contenido asociado al álgebra en tres categorías: ideas acerca de las funciones, escritura e interpretación de expresiones matemáticas.
Actualmente, las Bases Curriculares (Ministerio de Educación de Chile [MINEDUC], 2018) vigentes para los niveles de primero a sexto básico en Chile, manifiestan la introducción de ideas o conceptos de naturaleza algebraica. No obstante, fue en el año 2012 que el MINEDUC hizo efectiva la integración del álgebra desde primer año básico. Mejías (2019), con base en los documentos curriculares del año 2012, identifica la manera en que los objetos algebraicos son introducidos al currículo de educación básica en Chile. No obstante, el trabajo de este autor no aborda cómo los objetos y procesos de naturaleza aritmética pueden promover algún Nivel de Algebrización en el currículo de educación básica.
El objetivo de este artículo es, por un lado, identificar Niveles de Algebrización (en términos de objetos y procesos matemáticos, aritméticos y algebraicos) pretendidos por el currículo chileno de matemáticas para enseñanza básica (1° a 6° Básico), entendiendo currículo como la dupla <plan de estudios, libros de texto>, tal como sugieren Pino-Fan et al. (2013); y, por otro lado, caracterizar tipos de problemas que ponen en juego prácticas matemáticas que permiten promover determinados niveles del razonamiento algebraico en la enseñanza básica chilena.
2. NIVELES DE RAZONAMIENTO ALGEBRAICO EN EL CONTEXTO ONTOSEMIÓTICO
La presente investigación se sustenta en nociones teóricas desarrolladas por el Enfoque Ontosemiótico (EOS) del Conocimiento y la Instrucción Matemáticos (Godino et al., 2007), específicamente en la propuesta de Niveles de Algebrización (Godino et al., 2014). Los Niveles de esta herramienta teórico-metodológica “se definen teniendo en cuenta los tipos de representaciones usadas, los procesos de generalización implicados y el cálculo analítico que se pone en juego en la actividad matemática correspondiente (Godino et al., 2015, p. 117).
Actualmente, la propuesta del EOS de Niveles de Algebrización distingue siete niveles para el desarrollo progresivo del razonamiento algebraico, los primeros cuatro se asocian a la educación básica, y los restantes se asocian a la educación secundaria y bachillerato (Godino et al., 2015).
En este trabajo se consideran los niveles propuestos para la educación básica (Nivel 0 al Nivel 3). El Nivel 0 indica ausencia de razonamiento algebraico en las prácticas desarrolladas, y los dos Niveles siguientes (1 y 2), considerados como proto-algebraicos, sugieren indicios de ideas algebraicas durante el desarrollo de las prácticas matemáticas. Finalmente, el Nivel 3 indica una actividad matemática propiamente algebraica. A continuación, se presenta un resumen de estos Niveles y sus descriptores (Godino et al., 2014):
Nivel 0: Intervienen objetos extensivos (particulares) expresados mediante lenguaje natural, numérico, icónico o gestual. Pueden intervenir símbolos que refieren a un valor desconocido, obtenido como resultado de operaciones sobre objetos particulares. En tareas de generalización, el mero reconocimiento de la regla recursiva que relaciona un término con el siguiente, en casos particulares, no es indicativa de generalización.
Nivel 1: Intervienen objetos intensivos (generales) cuya generalidad se reconoce de manera explícita mediante lenguaje natural, numérico, icónico o gestual. Pueden intervenir símbolos que refieren a los intensivos reconocidos, pero sin operar con dichos objetos. Se identifican propiedades, equivalencias numéricas y relaciones a partir de tareas estructurales, mientras que en tareas funcionales se reconoce la generalidad expresada en un lenguaje diferente al simbólico-literal.
Nivel 2: Intervienen cantidades indeterminadas o variables expresadas con lenguaje simbólico o simbólico-literal para referir a los intensivos reconocidos, aunque ligados a la información del contexto espacio-temporal. En tareas estructurales, las ecuaciones son de la forma Ax±B =C . En tareas funcionales se reconoce la generalidad expresada en un lenguaje diferente al simbólico-literal.
Nivel 3: Son generados objetos intensivos representados de manera simbólica-literal y se opera con ellos; se elaboran transformaciones en la forma simbólica de las expresiones, conservando la equivalencia. Se realizan tratamientos con las incógnitas para resolver ecuaciones del tipo Ax±B = Cx±D , y la formulación simbólica y descontextualizada de reglas canónicas de expresión de funciones y patrones.
En esta investigación se concibe al razonamiento algebraico como aquél que “implica representar, generalizar y formalizar patrones y regularidades en cualquier aspecto de las matemáticas” (Godino y Font, 2003, p. 774). Para el caso de la educación básica, se puntualiza como Razonamiento Algebraico Elemental (RAE), definido como el “sistema de prácticas operativas y discursivas puestas en juego en la resolución de tareas abordables en la educación primaria en las cuales intervienen objetos y procesos algebraicos (simbolización, relación, variables, incógnitas, ecuaciones, patrones, generalización, modelación, etc.)” (Castro et al., 2011, p. 75).
Cabe señalar que en el EOS se entiende por práctica matemática “toda actuación o expresión (verbal, gráfica, etc.) realizada por alguien para resolver problemas matemáticos, comunicar a otros la solución obtenida, validarla o generalizarla a otros contextos y problemas (Godino y Batanero, 1994, p. 182). Por su parte, se consideran objetos algebraicos a las “relaciones binarias, operaciones y sus propiedades, funciones y estructura y sus tipos (semi grupo, monoide, semi módulo, grupo, módulo, cuerpo, espacio vectorial, etc.) propias del álgebra superior o abstracta” (Godino et al., 2012, p. 493).
Todo lo que se ha descrito, permite analizar de manera pormenorizada las prácticas desarrolladas o susceptibles de desarrollarse en torno a una tipología de tareas algebraicas. Conviene subrayar que,
Si bien los niveles proponen una gradación de las características algebraicas que pueden surgir en la solución de las tareas matemáticas escolares, se ha encontrado que es posible valorar una tarea como de un nivel u otro, en función del tipo de solución que se proponga, con lo cual la posible actividad matemática, de carácter algebraico, que un estudiante puede desarrollar, se predice en un rango aproximado. (Castro et al., 2017, p. 186)
3. CONTEXTO DE ESTUDIO Y METODOLOGÍA
Según lo señalado en el Art. 19 de la Ley General de Educación (N.º 20.370), la Educación Básica en Chile es el nivel orientado hacia la formación integral de los alumnos en diversas dimensiones, desarrollando sus capacidades de acuerdo a los conocimientos, habilidades y actitudes definidos en las Bases Curriculares. Estas últimas se determinan como el documento principal del currículo chileno, cuyo objetivo es que todos los estudiantes sean partícipes de una experiencia educativa similar, asentando una base cultural común (MINEDUC, 2018). Ellas establecen los Objetivos de Aprendizaje, que dan cuenta de los conocimientos, las habilidades y las actitudes que se deben aprender para satisfacer los objetivos generales de este nivel educacional. En particular, se establece para la asignatura Matemática que su propósito es
Enriquecer la comprensión de la realidad, facilitar la selección de estrategias para resolver problemas y contribuir al desarrollo del pensamiento crítico y autónomo en todos los estudiantes, sean cuales sean sus opciones de vida y de estudios al final de la experiencia escolar. (MINEDUC, 2018, p. 214)
La organización curricular de esta asignatura se presenta a través de: a) Habilidades, b) Ejes y c) Actitudes. Con respecto al apartado de Habilidades, se establece que cada una de estas (resolver problemas, representar, modelar, argumentar y comunicar) tiene un rol importante en la adquisición de nuevas destrezas y conceptos, así como en la aplicación de conocimientos para resolver las tareas matemáticas y de otros ámbitos. Los conceptos matemáticos se presentan en cinco ejes temáticos: Números y operaciones (Nyo), Patrones y álgebra (Pya), Geometría (Geo), Medición (Med), y Datos y probabilidades (Dyp).
En este artículo enfocamos nuestra atención en dos de los ejes, Nyo y Pya, en los cuales se presentan conceptos asociados al desarrollo del razonamiento algebraico. El eje Nyo, “abarca el desarrollo del concepto número como la destreza en el cálculo mental y el uso de algoritmos” (MINEDUC, 2018, p. 218). En el eje Pya, “se espera que los estudiantes establezcan relaciones entre números, formas, objetos y conceptos, con la finalidad de que sean capaces de indagar sobre las formas, las cantidades y el cambio de una cantidad en relación con otra” (MINEDUC, 2018, p. 219). Se señala que desarrollando una base sólida del concepto patrón se facilitaría el desarrollo de un pensamiento matemático más abstracto en los niveles superiores, como es el pensamiento algebraico.
A diferencia de las Bases Curriculares que rigen la educación de 7° básico a 2° medio (estudiantes de 12 a 15 años), donde se establece que los ejes de ‘Números’ y ‘Álgebra y funciones’ se relacionan fuertemente, en las Bases Curriculares de 1° a 6° básico no se hace alusión a ningún tipo de relación entre los ejes Nyo y Pya, lo que podría implicar que, en el caso del currículo chileno para la educación básica, la aritmética no se considere como una característica del RAE, y se considere solo a los objetos de naturaleza algebraica como elementos promotores de este.
Por otra parte, el MINEDUC pone a disposición de la comunidad educativa actividades complementarias, libros de actividades (cuadernillos de ejercicios), textos oficiales (guía didáctica del docente y texto del estudiante), imágenes, documentos interactivos, presentaciones de videos, entre otros, para cada uno de los niveles de la educación básica. En el caso de los textos del estudiante oficiales, se proponen seis (uno por cada nivel educativo) desde 1° a 6° básico (estudiantes 6 a 12 años), teniendo por objetivo exhibir los contenidos y requerimientos para cada uno de los niveles según lo planteado en las Bases Curriculares. La tabla 1 presenta algunos datos generales sobre los textos del estudiante distribuidos por el MINEDUC para seis de los ocho niveles de la Educación Básica en Chile. Cabe destacar que los textos no se estructuran en el mismo número de unidades y que estas pueden abordar más de un eje cada una.
Tabla 1 Organización de libros de texto chilenos por unidad y eje
| Nivel educativo | Autor(es) | Organización del texto por unidades y ejes | |||||
|---|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | ||
| 1° básico | Cortés (2018) | Nyo |
Geo Med |
Nyo | Pya | Dyp | Nyo |
| 2° básico | Ayala et al. (2017) |
Nyo Med |
Nyo Med Geo |
Nyo Pya Geo Dyp |
Nyo Med Dyp |
||
| 3° básico | Urra et al. (2017) | Nyo |
Nyo Pya Med Geo |
Nyo Pya Med Dyp |
Nyo Geo Med |
||
| 4º básico | Rodríguez et al. (2018) |
Nyo Pya |
Geo | Nyo | Med | Dyp | |
| 5º básico | Kheong et al. (2015/2017) |
Nyo Pya |
Geo Med |
Nyo Pya |
Dyp | ||
| 6° básico | Maldonado y Castro (2016) | Nyo | Pya |
Geo Med |
Dyp | ||
Fuente: Elaborado por los autores
3.1. METODOLOGÍA
La investigación se ha desarrollado bajo las características del paradigma cualitativo (Creswell, 2009; León y Montero, 2003). La técnica de investigación es el análisis de contenido (Gil, 1994), específicamente de las prácticas matemáticas institucionales (propuestas en los textos oficiales). Es pertinente señalar que, actualmente, la práctica de la enseñanza se sigue apoyando mayoritariamente en el libro de texto, teniendo una gran influencia en el aula, ya que sigue considerándose como uno de los referentes exclusivos del saber científico, influenciando las concepciones curriculares y siendo una de las principales fuentes que proporciona actividades de instrucción para los profesores (Espinoza et al, 2013; García-Mateos y Caballero-García, 2005; Pino-Fan et al, 2013). Asimismo, se considera que los análisis didácticos de libros de texto permiten, entre otras cosas,
caracterizar la calidad de la organización matemática textualizada, su grado de completitud, pertinencia, adecuación e idoneidad epistémica y didáctica, y en tal sentido, orientar al profesor para sostener un trabajo de gestión de la clase o rediseño de actividades científicamente sustentable y fundamentado. (Espinoza et al., 2013, pp. 5051-5052)
Es por lo anterior que se considera llevar a cabo un estudio didáctico a los textos de educación básica de Chile, propuestos para la asignatura de Matemática, con la finalidad de caracterizar, con base en las prácticas matemáticas de referencia (i.e., que los textos realizan y que se espera que realicen los estudiantes), los Niveles de algebrización pretendidos en el currículo de educación básica chileno.
Para efectos metodológicos, este trabajo adopta el modelo de Niveles de Algebrización (Godino et al., 2014) como herramienta de análisis. El análisis de los textos se desarrolla en las siguientes fases: 1) estudio preliminar y selección de los problemas asociados a los ejes Números y operaciones (Nyo) y Patrones y álgebra (Pya) del currículo escolar chileno; 2) resolución de los problemas seleccionados y análisis pormenorizado de las prácticas matemáticas de referencia; 3) generación de las categorías de problemas. Se analizan los seis textos del estudiante presentados en la tabla 1.
4. RESULTADOS DEL ANÁLISIS DE LOS LIBROS DE TEXTO
Los análisis realizados permitieron identificar que los Niveles de Algebrización pretendidos en el currículo chileno de matemática para la educación básica, van desde el Nivel 0 (ausencia del razonamiento algebraico) hasta un Nivel consolidado de Algebrización (Nivel 3). Se presentan con profundidad los análisis y resultados sobre los libros de texto utilizados en los cursos 1º (sección 4.1) y 4º año básico (sección 4.2). La elección de los libros de tales niveles se debe a que la diferencia es mínima entre 1º y 2º básico en lo que respecta al tipo de problemas y Niveles de Algebrización identificados y, además, porque de acuerdo al currículo de matemáticas en Chile, es en 4º básico cuando se introduce formalmente la notación algebraica. No obstante, antes de finalizar este apartado, se presentan de manera resumida los resultados para los libros de texto correspondientes a los cursos 2º, 3º, 5º y 6º básico (sección 4.3).
Para los cursos de 1º y 4º básico se describen con detalle las prácticas matemáticas de referencia, es decir, aquellas prácticas propuestas tal como aparecen en los libros de texto. mediante la identificación de los objetos matemáticos primarios que emergen o intervienen en estas prácticas, incluyendo ejemplos significativos de la caracterización de problemas que se ha realizado. Al final de cada sección, se establecen las características principales de los Niveles de Algebrización identificados. Esta misma estructura se sigue, de manera más resumida, con los cursos 2º, 3º, 5º y 6º básico.
4.1. PRIMERO BÁSICO: OBJETOS MATEMÁTICOS Y NIVELES DEL ALGEBRIZACIÓN IDENTIFICADOS
En este nivel se han caracterizado 14 tipos de situaciones-problema (rotuladas como SP) asociados a prácticas matemáticas promotoras del RAE donde cada una de estas prácticas se vinculan a un solo Nivel de Algebrización. La tabla 2 presenta, en la primera columna, los ejes temáticos de interés (Nyo, Pya) de la asignatura Matemática; en la segunda, se asigna un número a cada SP del libro de texto de 1º básico; en la tercera, las tipologías de problemas y, en la cuarta, el número de SP presentes en el libro de texto.
Tabla 2 Categorización de tipos de problemas en 1º básico
| Eje | SP | Tipo de problema | Número de SP contenidos en el texto |
|---|---|---|---|
| Número y operaciones | 1 | Aplicar el algoritmo de “componer y descomponer” cantidades numéricas para resolver problemas | 36 |
| 2 | Comparar cantidades (mayor que, menor que o igual que, es más que, es menos que) | 27 | |
| 3 | Determinar la cardinalidad de conjuntos | 29 | |
| 4 | Identificar a la suma y la resta como operaciones inversas | 4 | |
| 5 | Identificar el antecesor o sucesor de un número | 5 | |
| 6 | Identificar la condición para saber cuándo un elemento pertenece a un conjunto | 1 | |
| 7 | Identificar la función ordinal de los números naturales | 6 | |
| 8 | Identificar y representar mediante un número la cardinalidad de un conjunto | 11 | |
| 9 | Operar cantidades numéricas (suma o resta) | 34 | |
| 10 | Utilizar el algoritmo “abreviado” para sumar y restar | 7 | |
| Patrones y álgebra | 11 | Determinar los elementos de una secuencia dada la regla de formación | 5 |
| 12 | Identificar la regla (patrón) de formación | 16 | |
| 13 | Identificar la regla (patrón) de formación y completar la sucesión | 37 | |
| 14 | Resolver (implícitamente) ecuaciones de la forma 𝑥 ± 𝐵 = 𝐶 con 𝑥, 𝐵 y 𝐶 ∈ ℕ | 16 | |
| Total | 234 |
Fuente: Elaborado por los autores
4.1.1. Prácticas matemáticas asociadas al Nivel 0 de Algebrización
Los objetos matemáticos identificados en las prácticas matemáticas son:
Lenguaje. Predomina el lenguaje natural y representaciones numéricas e icónicas. Intervienen símbolos, como “⎕”, que representan a un valor desconocido (por ejemplo, en la expresión 7 = ⎕ + 2), pero dicho valor se obtiene como resultado de operaciones sobre objetos particulares. Los símbolos que intervienen se refieren a ejemplos o casos particulares (extensivos).
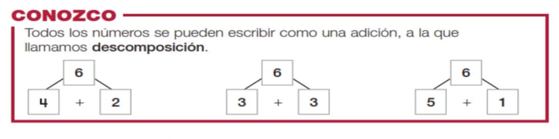
Definiciones-conceptos. Las definiciones se presentan mediante lenguaje materno o natural, apoyados además por figuras o íconos (ver figura 1), o lenguaje numérico-simbólico (números o signos, como +, -, =, entre otros). El concepto de número se asocia a la cardinalidad de un conjunto, o bien, con definiciones expresadas en lenguaje natural, “Los números tienen diferentes funciones, una de ellas es ordenar. A estos números se les llama números ordinales. 1º, 2º, 3º, 4º, 5º, 6º, 7º, 8º, 9º, 10º” (Cortés, 2018, p. 38).
Proposiciones. Las proposiciones se enuncian mediante el lenguaje natural, acompañadas de representaciones icónicas que apoyan de manera visual a las proposiciones dadas (ver figura 2).
Procedimientos. Los procedimientos son de naturaleza aritmética. Para obtener un valor desconocido, por ejemplo 5 + 4 = ⎕, se sugiere hacer uso de una cinta numerada y comenzar a contar, para este caso comenzando del 5 y contar 4 hacia adelante. La acción de contar es una técnica que prevalece a lo largo del libro de texto (contar los elementos en colecciones) para establecer la cardinalidad de los conjuntos, o bien, para comparar colecciones de elementos.
Argumentos. Los argumentos se valen de la observación y de la aplicación de estrategia o su verificación para establecer resultados. La figura 3 ejemplifica este tipo de argumentos.
Lo anterior permite concluir que las prácticas matemáticas son desarrolladas en un contexto puramente aritmético, donde los objetos matemáticos son expresados, principalmente, mediante los lenguajes natural, numérico e icónico y los cuales son ejemplos particulares de tipologías más amplias (por ejemplo, trabajar en el contexto de los números naturales). Además, los símbolos que refieren a valores desconocidos se obtienen como resultado de operaciones sobre objetos particulares (por ejemplo, la acción de agregar, que se traduce en lenguaje matemático como la operación suma 2 + 4 = ⎕).
4.1.2. Prácticas matemáticas asociadas al Nivel 1 de Algebrización
Para este nivel educativo se han caracterizado 4 tipos de problemas etiquetados en la segunda columna de la tabla 2 como SP11, SP12, SP13 y SP14, e identificados en la unidad dedicada al eje Pya. Las prácticas matemáticas promovidas en el texto, asociadas a la tipología de problemas antes mencionadas, permitieron identificar aspectos característicos del Early Algebra tales como la generalización de patrones, el desarrollo y manipulación del simbolismo en un lenguaje diferente al algebraico, así como el concepto de igualdad. Los objetos identificados en las prácticas matemáticas analizadas son:
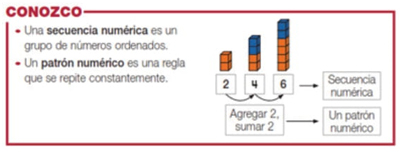
Lenguaje. Los patrones, secuencias y ecuaciones, se representan principalmente mediante lenguaje icónico, numérico y lenguaje natural. Los patrones y secuencias pueden encontrarse a partir de representaciones icónicas o bien representadas mediante lenguaje numérico (ver figura 4). Por otra parte, la idea de ecuación (de manera implícita) comienza a introducirse a través de representaciones icónicas, principalmente usando el concepto de balanza.
Definiciones-conceptos. Las definiciones o conceptos se enuncian a través de lenguaje natural, con apoyo de representaciones icónicas para dar explicaciones sobre estos (ver figura 5).
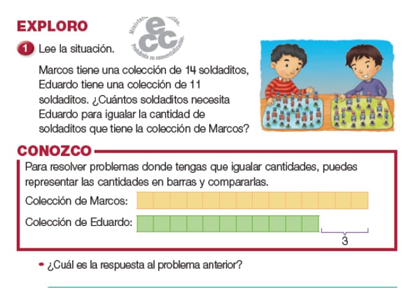
Proposiciones. Las proposiciones generalmente se enuncian mediante el lenguaje natural. Por ejemplo “Para resolver problemas donde tengas que igualar cantidades, puedes representar las cantidades en barras y compararlas” (Cortés, 2018, p. 160).
Procedimientos. Los procedimientos permiten identificar propiedades o equivalencias numéricas. La identificación de patrones numéricos, así como la determinación de los elementos de una secuencia, dada la regla de formación, se asocia a las acciones de agregar o quitar elementos (sumar o restar, respectivamente). El concepto de igualdad (o desigualdad) se aborda recurriendo a las técnicas de conteo (determinar la cardinalidad de conjuntos y compararlos). Implícitamente se trabaja con la noción de lo desconocido, para ello se recurre a equilibrar balanzas agregando o quitando elementos para lograr el equilibrio.
Argumentos. Los argumentos se valen de la observación y la aplicación de algunas estrategias o su verificación (ver Figura 6).
Para este nivel se han identificado en las prácticas matemáticas equivalencias numéricas (que se trabajan mediante el uso de balanzas) y relaciones a partir de tareas estructurales (mediante la composición y descomposición de los números, por ejemplo, descomponer el 7 como la suma de dos números diferentes, 5+2 o 2 + 5). Para el caso de las tareas de generalización de patrones (generación de secuencias o identificación de reglas de formación) se reconoce la generalidad, aunque expresada en un lenguaje diferente al simbólico-literal, etiquetados en la tabla 2 (columna SP con los números 11, 12 y 13).
4.2. CUARTO BÁSICO: OBJETOS MATEMÁTICOS Y NIVELES DE ALGEBRIZACIÓN IDENTIFICADOS
Para este nivel educativo se han caracterizado 14 tipos de situaciones-problema (SP) asociados a prácticas matemáticas promotoras del RAE. A diferencia del texto para 1º básico (ver tabla 2), estas prácticas se vinculan a más de un Nivel de Algebrización, por ejemplo, un problema del tipo ‘identificar la regla o patrón de formación’, puede resolverse mediante prácticas del Nivel 1 o 2 de Algebrización; lo mismo sucede cuando se resuelven ecuaciones de las formas x±B = C , B±x = C (con x, B, C ∈ ℕ). Otra diferencia es que, en este libro de texto, se han agrupado algunos de los problemas en ‘grandes categorías’, referidas a aquellas SP particulares que buscan el mismo objetivo. Por ejemplo, un problema de tipo ‘aplicar estrategias de cálculo mental’, puede ser ‘aplicar e identificar las propiedades del 0 y 1 en las operaciones de multiplicación y división’, o bien, ‘aplicar el algoritmo de la división para resolver problemas’.
En la tabla 3 se presentan en una primera columna los ejes temáticos de interés (Nyo, Pya) de la asignatura Matemática; en la segunda, se asigna un número a cada SP del libro de texto de 4º básico; en la tercera, las tipologías de problema y, en la cuarta, el número de SP presentes en el libro de texto.
Tabla 3 Categorización de tipos de problemas en 4º básico
| Eje | SP | Tipo de problema | Número de SP contenidos en el texto |
|---|---|---|---|
| Números y operaciones | 1 | Aplicar estrategias de cálculo mental | 42 |
| 2 | Comparar cantidades (mayor que, menor que o igual que, es más que, es menos que <, >, =) | 16 | |
| 3 | Comparar y ordenar cantidades (mayor que, menor que o igual que, es más que, es menos que, <, >, =) | 9 | |
| 4 | Identificar y representar mediante un número la cardinalidad de un conjunto | 14 | |
| 5 | Operar cantidades numéricas | 10 | |
| 6 | Representar y resolver problemas a través de: números decimales, racionales positivos, decimales y racionales | 42 | |
| 7 | Resolver problemas (suma y/o resta) a través de la aproximación (redondeo) de cifras | 6 | |
| 8 | Resolver problemas haciendo uso de una de las operaciones básicas (suma, resta, multiplicación y división) | 35 | |
| 9 | Resolver problemas haciendo uso de las cuatro operaciones básicas (suma, resta, multiplicación y/o división) | 3 | |
| Patrones y álgebra | 10 | Determinar los elementos de una secuencia dada la regla de formación | 5 |
| 11 | Identificar la regla (patrón) de formación | 3 | |
| 12 | Identificar la regla (patrón) de formación y completar la secuencia | 11 | |
| 13 | Representar y/o resolver ecuaciones de la forma 𝑥 ± 𝐵 = 𝐶, 𝐵 ± 𝑥 = 𝐶, con 𝑥, 𝐵 y 𝐶 ∈ ℕ | 25 | |
| 14 | Representar y/o resolver inecuaciones de la forma , 𝑥 ± 𝐵 < 𝐶, 𝑥 ± 𝐵 > 𝐶, con 𝑥, 𝐵 y 𝐶 ∈ ℕ | 30 | |
| Total | 251 |
Fuente: Elaborado por los autores
4.2.1. Prácticas matemáticas asociadas al Nivel 0 de Algebrización
Las prácticas matemáticas asociadas a este Nivel se caracterizan por el trabajo en el contexto de los números naturales y racionales positivos (fracciones o en su representación decimal). Los objetos matemáticos identificados son:
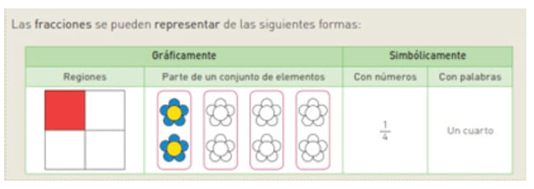
Lenguaje. Predomina el lenguaje numérico (cantidades hasta el 10,000), apoyado de rectas numéricas y tablas de valor posicional, bloques multibase, entre otros. Las fracciones (propias e impropias) se representan en la recta numérica, y por medio de lenguaje gráfico, simbólico, como la parte de un todo y mediante lenguaje natural (ver figura 7). Los números decimales se encuentran en forma numérica y apoyados por representaciones gráficas (por ejemplo, en regiones).
Definiciones-conceptos. Algunas definiciones y conceptos de este libro se encuentran en su glosario; otros, por ejemplo el concepto de descomposición aditiva (estrategia de cálculo), se presentan como un procedimiento (ver figura 8).
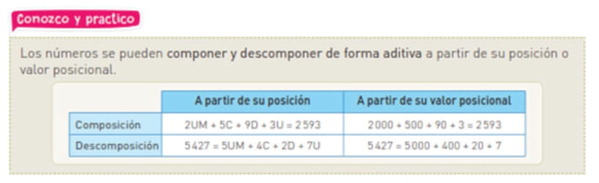
Proposiciones. Estos objetos matemáticos se enuncian en los apartados de Conozco y practico, como expresiones verbales que acompañan a procedimientos o definiciones y conceptos. Por ejemplo, se afirma que “los números se pueden componer y descomponer de forma aditiva a partir de su posición o valor posicional” (Rodríguez et al., 2018, p. 36).
Procedimientos. Al igual que las proposiciones, estos se enuncian frecuentemente en los apartados de Conozco y practico a través de los lenguajes natural o numérico. En su mayoría, los procedimientos se presentan apoyados con tablas, donde se colocan los algoritmos que se espera que los estudiantes repliquen en ejercicios posteriores o bien en representaciones icónicas (pictóricas) de las operaciones a realizar (ver figura 9).

Figura 9 Procedimientos para la adición de fracciones con igual denominador (Rodríguez et al., 2018, p. 215)
Argumentos. Los argumentos también se encuentran en los apartados de Conozco y practico. Se enuncian como ejemplos apoyados en figuras o procedimientos de carácter pictórico. En la figura 9, el argumento que valida el procedimiento corresponde al enunciado “puedes representar las fracciones usando diferentes colores, y el resultado corresponderá a todo lo pintado”. Además, la observación es una de las principales actividades utilizada para argumentar.
Se concluye que los objetos matemáticos se expresan mediante los lenguajes natural, numérico (naturales, fracciones y números decimales), icónico y tabular. Los valores desconocidos se obtienen mediante operaciones (multiplicación y división con cantidades menores a 10,000, o sumas y restas de fracciones o decimales), es decir, operando sobre objetos particulares.
4.2.2. Prácticas matemáticas asociadas al Nivel 1 de Algebrización
En este caso las prácticas matemáticas asociadas al Nivel 1 de Algebrización para este grado educativo se identifican tanto en el eje de Nyo como en el eje de Pya. Los objetos matemáticos identificados en el texto son:
Lenguaje. Se identifica el uso de los lenguajes numérico, verbal, tabular, e icónico. En las tareas de estructura donde se pide identificar o hacer uso de propiedades, los lenguajes numérico y verbal son los predominantes; por otra parte, las prácticas asociadas a SP10, SP11 y SP12 (ver tabla 3) se realizan principalmente a través de los lenguajes numérico y tabular. Las prácticas asociadas a las SP13 y SP14 se trabajan a través de lenguaje icónico (uso de balanzas) y se comienza a hacer uso de símbolos o letras (como x, y y z) para designar lo desconocido, definiéndolos como incógnitas.
Definiciones-conceptos. Se presentan en los apartados de Glosario y Conozco y practico, generalmente mediante lenguaje natural, con apoyo en el uso de ejemplos (tablas, algoritmos, figuras, etc.). Entre las definiciones o conceptos asociados a las prácticas de SP1, se encuentran las propiedades del 0 y el 1 en la multiplicación y división, y la propiedad distributiva. Para las tareas propias del eje Pya (ver tabla 3, números 10, 11 y 12), las prácticas matemáticas movilizan los conceptos de patrón numérico de adición, patrón numérico de sustracción, patrón numérico de multiplicación, patrón numérico de división, secuencia numérica, secuencia de figuras, crecimiento, disminución. Para las prácticas de las SP13 y SP14, los conceptos que se identifican son ecuación, incógnita, símbolo o letra (x, p, r, ℯ, etc.), modelar, balanza equilibrada, operación inversa, lados izquierdo y derecho de la ecuación.
Proposiciones. Las proposiciones se presentan en los apartados de Conozco y practico también mediante lenguaje natural. Generalmente, las proposiciones se enuncian al principio o al final de la sección antes mencionada. Algunas de las proposiciones que se encuentran son: “Al multiplicar cualquier número por 1, el producto es el mismo número, mientras que al multiplicar cualquier número por 0, es producto siempre es 0” (Rodríguez et al., 2018, p. 85); “Para multiplicar por 4 puedes multiplicar por 2 y el resultado multiplicarlo por 2” (Rodríguez et al., 2018, p. 65), entre otros.
Procedimientos. Los procedimientos son numéricos, tabulares y figurales (icónicos). Para las tareas de tipo estructural se hace uso de la propiedad distributiva para obtener el resultado de una multiplicación de un número de tres dígitos (ver figura 10). En tareas funcionales los procedimientos se apoyan en el uso de tablas para determinar características como la disminución o aumento en una sucesión con el objetivo de identificar el patrón de formación, lo cual se reproduce en tareas donde se identifican patrones numéricos de adición, sustracción, división y/o multiplicación.
Argumentos. Estos objetos se apoyan en la observación, se presentan en lenguaje natural, auxiliándose de tablas u operaciones aritméticas, así como en figuras (iconos) que representan a los objetos matemáticos. En la figura 10 los argumentos se representan con ejemplos que afirman las proposiciones que se establecen.
En síntesis, se ha identificado que en las prácticas matemáticas intervienen símbolos ( , y ) que refieren a ejemplos reconocidos (números, principalmente), pero no se opera con dichos objetos. Se identifican propiedades (del 0 y el 1 en la multiplicación y división, propiedad distributiva), equivalencias numéricas usando la balanza, mientras en tareas sobre generalización de patrones se reconoce la generalidad, aunque expresada en un lenguaje diferente al simbólico-literal (identificar la regla o el patrón de formación).
4.2.3. Prácticas matemáticas asociadas al Nivel 2 de Algebrización
Este Nivel de Algebrización se ha identificado solamente en prácticas matemáticas asociadas a las SP11, SP12, SP13 y SP14 (ver tabla 3) presentadas en el eje Pya. Se describen los objetos matemáticos identificados en el texto para este Nivel:
Lenguaje. Se comienza a hacer uso de lenguaje simbólico-literal en situaciones-problema asociadas a la resolución y/o representación de ecuaciones (x ± B = C, B ± x= C con x, B y C ∈ ℕ) e inecuaciones (x ± B< C, x ± B > C, con x, B y C ∈ ℕ). Predomina el lenguaje natural, seguido de los lenguajes numérico y tabular, se observa además el uso de lenguaje icónico (figural) para representar sucesiones o ecuaciones e inecuaciones (ver figura 11).
Definiciones-conceptos. Estos objetos matemáticos se encuentran en las secciones Glosario y Conozco y practico. Se presentan mediante lenguaje natural apoyados por representaciones de tipo simbólico-literal, tablas e iconos que permiten ejemplificarlas. Entre las definiciones se encuentran: ecuación, incógnita, modelar, operación inversa, patrón numérico, secuencia, valor encontrado, inecuación, balanza en desequilibrio, conjunto de números como solución. La figura 12 presenta la definición de inecuación.
Proposiciones. Se presentan en las secciones Conozco y practico. Aparecen mediante lenguaje natural, y se asocian con aspectos referentes a la resolución de ecuaciones o inecuaciones, así como con la identificación de patrones. Un ejemplo asociado a la identificación de patrones es “cuando la diferencia entre 2 números consecutivos de una secuencia numérica no es siempre la misma, puedes identificar un patrón de multiplicación o división” (Rodríguez et al., 2018, p. 97).
Procedimientos. Aquí destacan aquellos donde las estrategias se direccionan a la manipulación de las incógnitas. Estas estrategias son aquellas donde se hace uso de la operación inversa para resolver ecuaciones de la form a 𝑥 ± 𝐵 = 𝐶, 𝐵 ± 𝑥 = 𝐶, con 𝑥, 𝐵, 𝐶 ∈ ℕ (ver figura 13). Otra de estas estrategias versa en la sustitución del valor encontrado para comprobar las soluciones; para el caso de las inecuaciones se encuentran los procedimientos de ensayo y error y el uso de balanzas, mientras que para la comprobación se recurre a la sustitución del conjunto de valores encontrado en la representación simbólico-literal.

Figura 13 Operación inversa como estrategia para resolver ecuaciones (Rodríguez et al., 2018, p. 103)
Argumentos. Se presentan mediante los lenguajes natural, numérico e icónico. Los argumentos se basan en la observación y en las operaciones numéricas para refutar o no los resultados obtenidos. La figura 14 muestra un argumento apoyado en elementos visuales y numéricos.
Sintéticamente, se identificó la intervención de cantidades indeterminadas (lo desconocido) expresadas mediante lenguaje simbólico (x o y) que refiere a los intensivos reconocidos, aunque ligados a contextos específicos. Los procedimientos o estrategias de resolución se comienzan a direccionar a la manipulación de tales incógnitas para resolver ecuaciones e inecuaciones de las formas 𝑥 ± 𝐵 = 𝐶, 𝐵 ± 𝑥 = 𝐶,𝑥 ± 𝐵 < 𝐶, 𝑥 ± 𝐵 > 𝐶, con 𝑥, 𝐵, 𝐶 ∈ ℕ. Se identifican tareas donde se reconoce la generalidad (patrones numéricos), aunque expresada en un lenguaje diferente al simbólico-literal.
4.3. RESULTADOS DE LOS ANÁLISIS REALIZADOS A LOS TEXTOS DE 2º, 3º, 5º Y 6º BÁSICO
Se presentan, grosso modo, los resultados obtenidos del análisis de los textos para los niveles educativos de 2°, 3°, 5° y 6° básico. Para el segundo básico se han identificado 12 tipos de problemas asociados al desarrollo del RAE propuestos tanto en el eje de Nyo como el de Pya. Las prácticas matemáticas analizadas se asocian solo a los Niveles 0 y 1; a diferencia del texto de 1° básico, en el cual existen prácticas matemáticas promovidas, en el eje Nyo, propias del Nivel 1. En las prácticas matemáticas asociadas al Nivel 0, predomina el lenguaje de tipo numérico, seguido del lenguaje natural con el cual se describen conceptos-definiciones, proposiciones, procedimientos y argumentos; el lenguaje icónico sirve como apoyo visual, principalmente para los procedimientos. La noción de lo desconocido se vincula al trabajo aritmético (sentencias numéricas, por ejemplo, 40 + 18 = ⎕) y el valor se obtiene como resultados de operaciones (sumas o restas) sobre objetos particulares (números).
Con respecto a las prácticas matemáticas asociadas al Nivel 1, los objetos matemáticos se presentan mediante lenguajes natural, numérico, icónico y tabular. En tareas estructurales se reconocen propiedades como la conmutativa (por ejemplo, se le solicita al estudiante que observe la sentencia 12 + 5 = 5 + 12 y pinte V si la sentencia es verdadera o F si es falsa, argumentando su respuesta), así como equivalencias numéricas (presentadas generalmente haciendo uso del concepto de balanza). Los patrones se presentan mediante los lenguajes numérico e icónico y la generalidad se reconoce en un lenguaje diferente al simbólico-literal.
En el texto de 3° básico se caracterizaron 15 tipos de problemas, las prácticas vinculadas a éstos se asocian a los Niveles 0, 1 y 2 de Algebrización. Las prácticas matemáticas de los Niveles 0 y 1 comparten características de las antes descritas, pero para este nivel educativo se amplía el estudio a las operaciones de multiplicación y división, los números naturales se trabajan hasta el 1000; se comienza a hacer uso de la recta numérica y se inicia el estudio de las fracciones (representación y comparación, respectivamente).
En las prácticas del Nivel 2 de Algebrización se introducen nociones como ecuación, patrón, igualdad y desigualdad. Las tareas se asocian a la descripción y registro de patrones en secuencias numéricas y figurales, así como en tablas de 100, mediante estas tareas se reconoce la generalidad, aunque expresada en un lenguaje diferente al simbólico-literal. Se representan ecuaciones (mediante balanzas y sentencias del tipo a+ ⎕=b, ⎕ +a =b, donde a y b son números naturales) resueltas mediante la suma y la resta en contextos de resolución de problemas. Las incógnitas se representan mediante figuras (cuadrados, triángulos, círculos, entre otros).
Para 5° básico se han caracterizado 23 tipos de problemas asociados a prácticas matemáticas que movilizan objetos hasta del Nivel 3 de Algebrización, esto implica el trabajo en contextos algebraicos. La actividad aritmética (prácticas del Nivel 0) se desarrolla en contextos con números naturales (hasta el 1.000.000.000) y números racionales positivos (representados mediante fracciones y números decimales). El valor de lo desconocido se obtiene como resultado de operaciones sobre números o representaciones icónicas (para situaciones asociadas a las fracciones). En el caso de las fracciones y números decimales las operaciones se restringen a la suma y resta, mientras que en el contexto de los números naturales se recurre a las cuatro operaciones básicas.
Con respecto a los Niveles proto algebraicos (Niveles 1 y 2), se identifican en ambos ejes. Para el Nivel 1, las prácticas matemáticas vinculadas a tipos de problemas en el eje Nyo versan sobre el trabajo con propiedades de los números y operaciones (por ejemplo, aplicar e identificar las propiedades del 0 y 1 en las operaciones de multiplicación y división, o aplicar las propiedades asociativa y distributiva para calcular productos), y además se identifica la noción de equivalencia numérica (fracciones equivalentes). Para el eje Pya, las tareas consisten en identificar patrones, principalmente numéricos, y completar secuencias numéricas (términos muy próximos al último elemento dado de la secuencia).
El Nivel 2 solo se identifica en prácticas matemáticas propuestas en el contexto del eje Pya. Las prácticas asociadas tratan sobre identificar patrones y completar secuencias, o bien determinar elementos de la secuencia dada la regla de formación, observándose la formulación de la regla general, expresada en un lenguaje diferente al simbólico-literal. Predomina el lenguaje natural, seguido de los lenguajes numérico, icónico y tabular. En tareas de tipo estructural, se identifica el uso de lenguaje simbólico-literal y se realizan tratamientos con las incógnitas para resolver ecuaciones de la forma 𝑥 ± 𝐵 = 𝐶, 𝐵 ± 𝑥 = 𝐶, así como inecuaciones de la forma 𝑥 ± 𝐵 < 𝐶, 𝑥 ± 𝐵 > 𝐶, con 𝑥, 𝐵 y 𝐶 ∈ ℕ.
Finalmente, el Nivel 3 se asocia con el eje Pya, específicamente con situaciones-problema donde la consigna es elaborar transformaciones de expresiones simbólicas, en particular reducirlas conservando la equivalencia (ver figura 15). Predominan los lenguajes simbólico e icónico, los conceptos-definiciones se vinculan con expresiones algebraicas, términos semejantes, variable. Los procedimientos se apoyan en recursos visuales para ejemplificar, entre otros, la reducción de términos algebraicos.
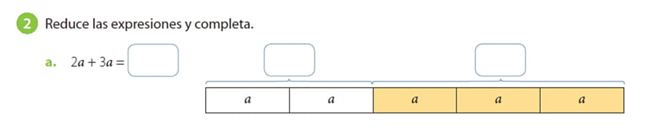
Figura 15 Tipo de problema Representar y transformar expresiones algebraicas (Kheong et al., 2015/2017, p. 259)
Los resultados para el 6° básico son análogos, en términos de los Niveles 0, 1 y 2 de Algebrización, a los obtenidos en el 5° básico. En cuanto a la caracterización de tipos de problemas, para este nivel educativo se han propuesto 28 categorías. En el contexto del eje Nyo se introducen conceptos como múltiplos y factores, números primos y compuestos, mínimo común múltiplo, razones y porcentajes; en el contexto de los números decimales se introducen las operaciones multiplicación y división; predomina el trabajo en contextos aritméticos, identificándose situaciones-problema asociadas al Nivel 1 de Algebrización (actividad matemática ligada a la identificación de propiedades de estructura).
En cuanto al Nivel 3 de Algebrización, se generan objetos intensivos representados de manera simbólico-literal, y se opera con ellos (expresiones algebraicas, principalmente) conservando la equivalencia; se generan reglas canónicas mediante lenguaje simbólico-literal y apoyados en tablas de valores, se evidencia actividad algebraica consolidada. Entre los conceptos destacan término general, regla, posición del término (n), relación, valor del término, lenguaje algebraico. Los argumentos se basan en el uso de propiedades, por ejemplo, la propiedad conmutativa (𝑎 + 𝑏 = 𝑏 + 𝑎) y+ en los contextos para verificar los valores obtenidos. Predomina el lenguaje algebraico, seguido de los lenguajes natural, numérico, icónico y tabular.
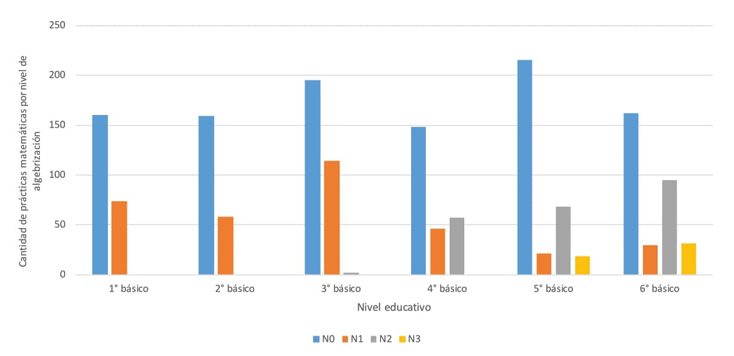
Resumiendo, se puede establecer que el currículo de Educación Básica en Chile, de primero a sexto básico, promueve prácticas matemáticas asociadas a los Niveles 0, 1, 2 y 3 de Algebrización. Como podría presuponerse, en el eje Pya se identificaron prácticas matemáticas en Niveles consolidados de Algebrización, en los cuales se establecen términos generales de una secuencia, así como la reducción de expresiones algebraicas, desarrolladas a través de lenguaje algebraico. En este eje se identificaron prácticas en Niveles menores de Algebrización (Niveles 0, 1 y 2). En ellas no se observa la manipulación ni el uso del lenguaje algebraico, sino que se establece, por ejemplo, a través de lenguaje numérico o materno, la generalización de patrones. Uno de los hallazgos más relevantes fue determinar que algunas de las prácticas matemáticas del eje Nyo, también son promotoras del RAE, aunque no en Niveles consolidados de Algebrización, sino en Niveles Proto-algebraicos (Niveles 1 y 2). A pesar de que hay un esfuerzo por introducir el álgebra temprana desde los primeros cursos, el tipo de tareas y prácticas son mínimas en cantidad comparadas con las tareas y prácticas de naturaleza aritmética en este eje, siendo las prácticas de Nivel 0 las que mayor presencia tienen en el currículo. La figura 16 muestra la cuantificación de prácticas de cada uno de los textos por Nivel de Algebrización.
La tabla 4 presenta la tipología de problemas identificadas en los textos de 2°, 3º, 5º y 6° básico, así como el número de prácticas matemáticas por Nivel de Algebrización.
Tabla 4 Prácticas matemáticas de referencia por tipo de problemas y Nivel de Algebrización
| Eje | SP | Tipo de problemas | Nivel educativo | Total | |||
| 2° | 3° | 5° | 6° | ||||
| Números y operaciones | 1 | Aplicar estrategias de cálculo mental |
20N0 1N1 |
33N0 |
21N0 7N1 |
1N1 | 83 |
| 2 | Comparar cantidades (mayor que, menor que o igual que, es más que, es menos que, <, >, =). | 17N0 |
26N0 4N1 |
22N0 | 7N0 | 76 | |
| 3 | Comparar y ordenar cantidades (mayor que, menor que o igual que, es más que, es menos que, <, >, =) | 10N0 | 9N0 | 10N0 | 1N0 | 30 | |
| 4 | Descomponer cantidades numéricas en factores primos | 2N0 | 2 | ||||
| 5 | Determinar el mínimo común múltiplo de cantidades numéricas | 3N0 | 3 | ||||
| 6 | Determinar múltiplos, factores y divisores de cantidades numéricas | 7N0 | 7 | ||||
| 7 | Estimar cantidades por medio del redondeo de cifras | 29N0 | 29 | ||||
| 8 | Identificar la condición para saber cuándo un elemento pertenece a un conjunto y resolver problemas | 2N0 | 2 | ||||
| 9 | Identificar los múltiplos de números naturales | 1N0 | 1 | ||||
| 10 | Identificar propiedades de las operaciones | 16N1 | 8N1 | 1N1 | 4N1 | 29 | |
| 11 | Identificar reglas y/o propiedades al trabajar con conjuntos de números (decimales, primos, compuestos, razones o porcentajes) | 3N1 | 3 | ||||
| 12 | Identificar reglas y/o propiedades del mínimo común múltiplo | 1N1 | 1 | ||||
| 13 | Identificar y representar mediante un número la cardinalidad de un conjunto | 21N0 | 4N0 | 1N0 | 26 | ||
| 14 | Operar cantidades numéricas (suma, resta, multiplicación y/o división) | 36N0 | 21N0 | 52N0 |
59N0 1N1 |
169 | |
| 15 | Realizar conversiones entre sistemas numéricos | 4N0 | 7N0 | 11 | |||
| 16 | Representar e identificar fracciones equivalentes | 6N1 | 10N1 | 12 | |||
| 17 | Representar problemas a través de expresiones numéricas | 1N0 | 1 | ||||
| 18 | Representar y resolver problemas a través de números racionales positivos (fracciones y/o decimales) | 58N0 |
49N0 2N1 |
109 | |||
| 19 | Representar y resolver problemas haciendo uso de razones y/o porcentajes | 23N0 | 23 | ||||
| 20 | Resolver problemas a través de una de las operaciones básicas | 48N0 | 96N0 | 26N0 |
32N0 1N1 |
203 | |
| 21 | Resolver problemas haciendo uso de dos o más de las operaciones básicas (suma, resta, multiplicación y/o división) | 13N0 |
5N0 1N1 |
19 | |||
| 22 | Resolver problemas haciendo uso del mínimo común múltiplo | 9N0 | 9 | ||||
| Patrones y álgebra | 23 | Determinar los elementos de una secuencia dada la regla de formación | 17N1 |
1N0 29N1 2N2 |
4N1 6N2 |
10N1 3N3 |
72 |
| 24 | Identificar expresiones algebraicas y/o numéricas | 1N2 | 1 | ||||
| 25 | Identificar la regla (patrón) de formación | 2N1 | 12N1 | 2N1 |
2N1 1N2 5N3 |
24 | |
| 26 | Identificar la regla (patrón) de formación y completar la secuencia | 12N1 | 35N1 |
7N1 5N2 |
7N1 12N2 8N3 |
81 | |
| 27 | Identificar la representación de ecuaciones de la forma 𝑥 ± 𝐵 = 𝐶, 𝐵 ± 𝑥 = 𝐶 con 𝑥, 𝐵, 𝐶 ∈ ℕ | 1N1 | 1N2 | 2 | |||
| 28 | Representar ecuaciones de la forma 𝑥 ± 𝐵 = 𝐶, 𝐵 ± 𝑥 = 𝐶 con 𝑥, 𝐵, 𝐶 ∈ ℕ | 4N1 | 5N2 | 9 | |||
| 29 | Representar y resolver ecuaciones de la forma 𝑥 ± 𝐵 < 𝐶, 𝑥 ± 𝐵 > 𝐶, con 𝑥, 𝐵 y 𝐶 ∈ ℕ | 12N1 | 18N2 | 34N2 | 64 | ||
| 30 | Representar y resolver inecuaciones de la forma 𝑥 ± 𝐵 = 𝐶, 𝐵 ± 𝑥 = 𝐶 con 𝑥, 𝐵 y 𝐶 ∈ ℕ | 7N2 | 7 | ||||
| 31 | Representar y transformar expresiones algebraicas | 19N3 | 2N2 | 21 | |||
| 32 | Representar y/o resolver problemas a través de expresiones algebraicas | 11N2 |
11N2 15N3 |
37 | |||
| 33 | Resolver (implícitamente) ecuaciones de la forma 𝑥 ± 𝐵 = 𝐶 con 𝑥, 𝐵, 𝐶 ∈ ℕ | 11N1 | 11 | ||||
| 34 | Resolver ecuaciones de la forma 𝑥 ± 𝐵 = 𝐶, 𝐵 ± 𝑥 = 𝐶 con 𝑥, 𝐵 y 𝐶 ∈ ℕ | 9N1 | 3N2 | 17N2 | 29 | ||
| 35 | Resolver inecuaciones de la forma 𝑥 ± 𝐵 < 𝐶, 𝑥 ± 𝐵 > 𝐶, con 𝑥, 𝐵 y 𝐶 ∈ ℕ | 2N2 | 2 | ||||
| 36 | Evaluar y/o comparar expresiones algebraicas | 16N2 | 8N2 | 24 | |||
Fuente: Elaboración de los autores
5. REFLEXIONES FINALES
Los resultados de esta investigación ofrecen información interesante sobre las características del RAE en el currículo de Educación Básica en Chile. Se ha evidenciado que no sólo las prácticas matemáticas asociadas al eje de Pya son promotoras de este tipo de razonamiento, pues los resultados apuntan a la existencia de prácticas matemáticas en el contexto aritmético que podrían catalogarse como promotoras del RAE, en Niveles incipientes de Algebrización. Entre las características identificadas del Álgebra temprana en el currículo de Chile, destacan conceptos como generalización de patrones, el desarrollo y manipulación del lenguaje simbólico-literal, y la resolución de ecuaciones e inecuaciones de primer grado (Molina, 2009). Otro resultado versa sobre la existencia de tareas transversales (ver SP1, SP23, SP25, SP26, SP29, SP32 y SP34 en tabla 4), es decir, tipos de SP presentes en dos o más cursos, y donde sus prácticas matemáticas progresan de lo concreto a lo pictórico (icónico) y, de ahí, a lo simbólico (abstracto), lo que, además, muestra que existe una progresión en los Niveles de Algebrización.
Además, se ha observado que un tipo de problema admite una o más prácticas matemáticas de referencia, las cuales pueden ser catalogadas en un Nivel u otro de Algebrización. Con esto se reafirma lo señalado por Godino y colaboradores (2014), “el nivel se asigna, no a la tarea en sí misma, sino a la actividad matemática que se realiza, por lo que dependiendo de la manera en que se resuelve una tarea, la actividad matemática puede ser clasificada en un nivel u otro” (p. 206). Si bien se ha identificado que el currículo de educación básica en Chile promueve prácticas matemáticas en Niveles consolidados de Algebrización, en la figura 16 se observa la poca presencia de este tipo de prácticas y el gran desequilibrio que existe entre el Nivel 0 y el resto de los Niveles de Algebrización.
Se esperaría que los Niveles 1, 2 y 3 se equilibraran de manera progresiva a lo largo de los seis niveles educativos, respecto de la cantidad de prácticas asociadas al Nivel 0. Sería conveniente aumentar en los textos el número de situaciones-problemas cuya resolución admita el uso de diversos Niveles de Algebrización. Asimismo, sería interesante que los libros destinados al profesor (Guía del Docente) proporcionen ejemplos sobre cómo, a partir de una determinada SP, del tipo ‘identificar la regla (patrón) de formación y completar la secuencia’ o ‘aplicar estrategias de cálculo mental’, se pueda ir variando la respuesta (i.e., uso de distintas prácticas matemáticas para la solución) buscando promover distintos niveles de RAE.
Como se ha planteado anteriormente, el objetivo de este estudio se centra en el análisis de las prácticas matemáticas de referencia (las propuestas por el MINEDUC) en los libros de texto, y no en las prácticas matemáticas personales de los estudiantes. Ello se justifica en que, si bien es importante conocer y analizar este último tipo de prácticas, el análisis de las prácticas matemáticas de referencia da conocimiento sobre cómo los estudiantes deberían resolver las tareas que se plantean en los textos de estudio supeditados a lo que se estipula en las Bases Curriculares para Educación Básica de Chile (MINEDUC, 2018). Además, se considera que la caracterización aquí realizada puede ser útil tanto para profesores en activo, como para futuros profesores de educación básica, ya que se considera la selección de tareas (problemas, ejercicios, actividades) propuestas en el currículo (planes de estudio, libro de texto), como una actividad característica de la práctica de enseñar matemáticas (Watson y Thompson, 2015). Se espera que esta caracterización permita a los investigadores y profesores contar con material para el diseño y desarrollo de SP vinculadas a la promoción del RAE, adecuadas al curso donde se propongan, e identificar así cuáles serían las prácticas matemáticas que se deberán poner en juego para promover un Nivel u otro de Algebrización.
Aunque a nivel internacional existe un gran número de investigaciones en la línea del Álgebra temprana, en el contexto chileno la realidad es distinta, ya que los estudios relacionados con este tema se circunscriben al trabajo de Mejías y colaboradores (Mejías, 2019; Mejías y Alsina, 2020), debido a la relativamente reciente integración del álgebra (desde 2012) a la Educación Básica, su adecuación curricular y posterior implementación (MINEDUC, 2018).
Los Niveles de Algebrización son considerados como una herramienta teórico-metodológica con gran potencial para predecir la actividad matemática asociada al desarrollo del RAE; sin embargo, el análisis desarrollado ha mostrado la necesidad de refinar los Niveles de Algebrización ya que existen prácticas matemáticas que no responden en su totalidad a las características de un Nivel u otro. Por ejemplo, en el estudio del objeto matemático patrón en los primeros niveles (1° y 2°, respectivamente), existen prácticas matemáticas en las que se trabaja vía ejemplos particulares que buscan reconocer el patrón de formación, relacionando un término con el siguiente (o con elementos cercanos al último elemento presentado en una secuencia), que permiten identificar aspectos relacionados con la generalización, expresados en un lenguaje diferente al simbólico-literal. Este ejemplo evidencia que, en respuestas esperadas o de los estudiantes, es posible adoptar de forma articulada los elementos de los Niveles 0 y 1 de Algebrización.
Se desconoce si las tareas propuestas en el currículo chileno cumplen con la generación de bases sólidas para el desarrollo del pensamiento algebraico en niveles educativos superiores a los aquí analizados. Se reconoce que los resultados obtenidos en esta investigación han sido fruto del análisis de textos del estudiante propuestos por el MINEDUC, existiendo otros textos autorizados para el estudiante de distribución privada, los cuales no fueron analizados en esta investigación. Queda como posible línea de continuidad estudiar si en ellos existen otro tipo de prácticas matemáticas asociadas al razonamiento algebraico promovido en la Educación Básica en Chile.











 nueva página del texto (beta)
nueva página del texto (beta)