1. INTRODUCCIÓN
Tradicionalmente los currículos de matemáticas han retrasado de forma explícita el estudio del álgebra a los primeros cursos de la educación secundaria, debido a que, según la teoría piagetiana, la escasa capacidad de abstracción de los alumnos de primaria no les permitía pasar del pensamiento operacional concreto al pensamiento formal algebraico.
Sin embargo, investigaciones en didáctica de las matemáticas han observado que los alumnos llegan al sistema educativo con capacidades naturales de generalización que permiten desarrollar el pensamiento algebraico (Mason, 1999) y que este está implícito en los alumnos de primaria (Socas, 2011). Otros investigadores complementan estas ideas al considerar que los alumnos de primaria son capaces de simbolizar algebraicamente conjeturas sobre relaciones aritméticas básicas (Carpenter et al., 2003), de considerar las operaciones aritméticas como funciones en vez de simples cálculos con números particulares (Schliemann et al., 2003), de trabajar con relaciones funcionales (Carraher et al., 2003) y de usar representaciones algebraicas, como gráficos y tablas, para resolver problemas (Brizuela y Schliemann, 2003).
A partir de estas investigaciones surgen corrientes, como la pre-álgebra o la early algebra, que proponen introducir el álgebra en la educación primaria. Ambas corrientes consideran necesario iniciar el pensamiento algebraico con actividades que involucren a los alumnos en procesos matemáticos como la identificación de las estructuras matemáticas, la generalización y la representación de relaciones, pero difieren en su finalidad y en el momento de introducción. Mientras la pre-álgebra intenta suavizar el paso de la aritmética al álgebra con una aritmética generalizada en los últimos años de la primaria, la early algebra propone introducir el pensamiento algebraico, de manera transversal, gradual y sistemática, desde los primeros años de escolarización, incorporando actividades dirigidas a la identificación de patrones, relaciones y propiedades matemáticas (Molina, 2009).
Ambas corrientes coinciden en que 1) no es preciso aumentar los contenidos, sino que deben ser tratados con más profundidad resaltando las ideas de generalización, estructura y relaciones, 2) la introducción temprana de temas algebraicos puede ayudar al alumno a adquirir un mejor nivel de análisis y de lógica, a realizar generalizaciones, utilizar símbolos y relaciones y 3) el desarrollo de estas capacidades evitaría problemas de aprendizaje del álgebra en los niveles medio y superior.
Para Kieran (2004) el álgebra es una forma de pensar que sirve para captar y explicar relaciones y considera que el pensamiento algebraico en las primeras etapas no debe centrarse en la mera presentación de las simbolizaciones pre-fabricadas (expresiones algebraicas), sino en actividades que “incluyan el análisis de relaciones entre cantidades, la identificación de estructuras, el estudio de los cambios, la generalización, la resolución de problemas, la modelación, la justificación, la prueba y la predicción” (Kieran, 2004, p. 149).
Para la introducción temprana del álgebra es preciso crear ambientes de instrucción para explicitar el pensamiento algebraico implícito en los alumnos de la Educación Primaria (Carpenter y otros, 2003) y el trabajo con patrones y el estudio de sus regularidades y propiedades pueden contribuir de forma eficaz a la creación de estos ambientes.
Desde esta perspectiva, el objetivo de este trabajo es analizar las respuestas de alumnos de primaria a un problema de generalización de patrones, estudiando los niveles de éxito, los grados de desarrollo y las estrategias usadas.
2. MARCO TEÓRICO
La generalización es uno de los procesos cognitivos más importantes de la actividad matemática y tiene un papel relevante dentro del álgebra. Así Mason, Burton y Stacey (1992), afirman que las generalizaciones constituyen el verdadero nervio de la matemática y Mason et al. (2005) señalan que la generalización es la esencia del álgebra y una de las rutas fundamentales hacia ella.
El proceso de generalización consiste en “pasar de un objeto a una clase que contiene el objeto” (Pólya, 1954, p. 12), en “derivar o inducir desde lo particular, identificando lo que es común y extendiendo dominios de validez para incluir un conjunto mayor de casos” (Dreyfus, 1991, p. 35) o en “aplicar un argumento dado en un contexto más amplio” (Harell y Tall, 1991, p. 38); es decir, generalizar es “ver lo general a través de lo particular y ver lo particular en lo general” (Mason et al., 2005 p. 310).
Para Radford (2006), la generalización de un modelo algebraico se basa en la capacidad de captar alguna regularidad observada en algunos elementos de una secuencia, siendo conscientes de que esta regularidad se aplica a todos los términos de la secuencia y siendo capaces de utilizarla para proporcionar una expresión directa de cualquier término de la secuencia. Kaput (1999) concreta esta idea al definir la generalización como la identificación y exposición de la regularidad o similitud entre casos particulares y la extensión del razonamiento a los patrones, estructuras y relaciones.
Así pues, generalizar es universalizar una propiedad observada en un número limitado de casos, e implica poner a los estudiantes en la necesidad de buscar pautas generales de comportamiento, reglas y leyes que se puedan expresar verbal o simbólicamente y que se puedan aplicar a cualquier caso que se presente, haciéndoles notar la insuficiencia del método experimental.
Radford (2008) concreta la generalización de patrones en tres etapas: en la primera etapa el estudiante observa una propiedad común en algunos términos de una secuencia y extiende la propiedad observada a términos cercanos (generalización cercana), en la segunda extiende la propiedad a términos lejanos (generalización lejana) y en la tercera obtiene una regla general que permite calcular cualquier término.
En la generalización de patrones se observan los dos momentos indisolubles de la abstracción reflexiva, que es el centro de la teoría de la construcción del conocimiento de Piaget (1977/2001): un proceso de reflexión o proyección en el que lo abstraído pasa de un plano inferior a otro superior y una reflexión que permite una reorganización cognitiva sobre el nuevo plano. En el plano inferior las acciones y operaciones se realizan sobre objetos concretos, físicos o imaginados, mientras que en el plano superior las acciones y operaciones actúan sobre objetos abstractos. De esta manera, los procesos de generalización cercana y lejana se establecen en el plano inferior y la obtención de la regla general en el superior.
En muchos problemas de generalización de patrones se especifican gráficamente los primeros términos f(1), f(2), f(3)… de una progresión aritmética f(n) a-n± b, y se pide (1) calcular f(n) para n pequeño (generación cercana), (2) calcular f(n) para n grande (generalización lejana) y (3) expresar la regla general (Autor, 2011). En algunos problemas también se incluye el proceso inverso, es decir, hallar n a partir de f(n).
En el paso de la generalización cercana a la generalización lejana se encuentra la frontera entre las generalizaciones que Radford (2008) denomina aritmética y algebraica. Mientras en la generalización cercana el estudiante inicia reconociendo el patrón de crecimiento, pero se limita a realizar un simple recuento, en la generalización lejana el recuento sería una tarea larga y laboriosa, por lo que debe extender el rango de aplicabilidad del patrón a cualquier término de la secuencia. De esta forma pasa de la concreción del recuento en los términos pequeños a la abstracción que supone la extensión del patrón a términos grandes. La expresión de la regla general que identifica y define el patrón se puede realizar de forma gráfica, verbal y/o algebraica. Radford (2008) considera esta etapa el punto crucial en el proceso de generalización y en la que los alumnos encuentran mayores dificultades ya que requiere una mayor capacidad de abstracción.
Las estrategias son los métodos para resolver problemas, “y suponen cualquier tipo de procedimiento que pueda ejecutarse, teniendo en cuenta las relaciones y los conceptos implicados (Rico, 1997, p. 31). Stacey (1989) observó cuatro estrategias distintas: recuento, diferencia entre términos consecutivos, función lineal y proporcionalidad directa. García Cruz (1989) estableció tres estrategias: esquema de recuento, esquema lineal y esquema de proporcionalidad directa. Lannin et al. (2006) definieron cinco estrategias: conteo, recursiva, múltiplo de la diferencia, razonamiento multiplicativo y correspondencia. Zapatera (2018), recopiló estas estrategias en tres grandes grupos: estrategias aditivas, estrategias funcionales y estrategias proporcionales (tabla 1).
Tabla 1 Estrategias de resolución de problemas de generalización de patrones
| Autor (2018) | Stacey (1989) | García Cruz (1989) | Lannin et al. (2006) | |
| E. aditivas | Recuento sobre dibujo | Recuento | Esquema de recuento | Conteo |
| Recuento iterativo | Diferencia | Recursiva | ||
| Recuento recursivo | Múltiplo de la diferencia | |||
| E. funcionales | Función local | Lineal | Esquema lineal | Correspondencia |
| Función global | ||||
| E. proporcionales | Proporcional | Esquema proporcional | Raz. multiplicativo |
Las estrategias aditivas se dividen en (1) recuento sobre el dibujo, si el alumno dibuja el término pedido y cuenta sus elementos, (2) recuento iterativo, si parte del primer término y suma la diferencia constante, o patrón de crecimiento, hasta llegar al término pedido y (3) recuento recursivo, si parte de un determinado término y suma la diferencia constante hasta llegar al término requerido. Las estrategias funcionales pueden ser (1) locales, si el alumno utiliza una función para hallar los elementos de un determinado término y (2) globales, si utiliza una función para hallar los elementos de un término cualquiera. Y en las estrategias proporcionales, el alumno utiliza erróneamente, la proporcionalidad directa (tabla 2).
3. METODOLOGÍA
3.1. PARTICIPANTES
En esta investigación han participado 106 estudiantes de 3º, 4º, 5º y 6º de Educación Primaria (8-12 años), que no habían recibido ninguna preparación específica en problemas de generalización de patrones.
3.2. RECOGIDA DE DATOS
El problema utilizado es una adaptación del problema de “las mesas y las sillas” de Carraher et al. (2008) (figura 2).
Para resolver la primera cuestión, el alumno debe descubrir el patrón de crecimiento, “añadir dos sillas”, para realizar la generalización cercana; en la segunda cuestión debe extender el rango del patrón hasta las 100 mesas, para realizar la generalización lejana; y en la tercera cuestión debe expresar una regla que permita hallar el número de sillas que se colocan alrededor de un número cualquiera de mesas.
3.3. ANÁLISIS DE DATOS
El análisis de datos se realiza en función de dos criterios: corrección de las respuestas y utilización de estrategias.
- Se considera que las dos primeras cuestiones están resueltas correctamente si calcula el número exacto de sillas que se necesitan y la tercera cuestión si expresa una regla que permita hallar el número de sillas a partir del número de mesas.
- Se consideran las estrategias recogidas en la figura 1, completadas con estrategia directa y otras. Un alumno utiliza la estrategia directa si escribe el número de sillas (niños) de forma directa y utiliza otra estrategia si utiliza una estrategia no recogida en las anteriores. De esta forma, las posibles opciones son: D (directa), RD (recuento sobre dibujo), RI (recuento iterativo), RR (recuento recursivo), FL (función local), FG (función global) y O (Otras).
El análisis se realiza en cinco etapas:
Nivel de éxito: se analiza el éxito conseguido por los alumnos por cursos y por etapas.
Grados de desarrollo: se establece un diagrama de flujo y se clasifican los alumnos en cuatro grados de desarrollo de la generalización de patrones.
Utilización de estrategias: se analizan las estrategias utilizadas por cuestiones y por cursos y el nivel de éxito de cada estrategia.
Secuencias de estrategias: se analizan las secuencias de estrategias utilizadas por los alumnos que hayan conseguido superar todo el proceso de generalización de patrones.
Estudio de casos: se presentan y estudian las respuestas de un alumno representativo de cada uno de los grados establecidos en la etapa 2.
4. RESULTADOS
En la tabla 2 se muestran los resultados obtenidos por los 106 alumnos según los dos criterios de análisis: las respuestas correctas están sombreadas y en la cada celda aparece la estrategia utilizada por cada alumno en cada cuestión.
Tabla 2 Resultados según corrección y estrategias usadas
| 3° curso | 4° curso | 5° curso | 6° curso | |||||||||
| C1 | C2 | C3 | C1 | C2 | C3 | C1 | C2 | C3 | C1 | C2 | C3 | |
| 1 | RD | D | EP | RD | FL | FL | RD | EP | O | FL | FL | FG |
| 2 | RD | EP | EP | D | FL | RR | RD | FL | FG | RD | FL | FG |
| 3 | RD | EP | O | D | FL | O | RD | EP | EP | RD | FL | FG |
| 4 | RD | D | O | RD | EP | EP | RD | FL | FG | FL | FL | FG |
| 5 | FL | FL | FL | RD | EP | EP | RD | FL | O | RD | FL | FG |
| 6 | EP | EP | EP | RD | FL | FL | RD | FL | FG | RD | FL | FG |
| 7 | RD | D | B | EP | EP | EP | RD | FL | FL | RD | FL | FL |
| 8 | RD | EP | EP | RD | FL | FL | RD | FL | FL | RD | FL | FG |
| 9 | RD | EP | RI | RI | EP | EP | RD | EP | EP | FL | FL | FG |
| 10 | EP | EP | B | EP | EP | EP | RD | EP | EP | RD | FL | EP |
| 11 | RD | EP | RR | RD | O | EP | RD | EP | EP | RD | FL | FG |
| 12 | RD | EP | EP | RD | FL | FG | RD | FL | FG | RD | EP | EP |
| 13 | D | D | B | RD | D | O | RD | FL | EP | FL | FL | FG |
| 14 | RD | D | EP | RD | D | RI | RD | FL | FG | RD | EP | EP |
| 15 | RD | EP | O | RD | EP | EP | RD | EP | EP | RI | EP | RI |
| 16 | RD | D | O | RD | O | O | FL | FL | FG | RD | FL | FL |
| 17 | RD | EP | EP | RD | EP | RI | RD | O | RI | RD | EP | FG |
| 18 | EP | O | O | RD | EP | EP | RD | FL | FG | RD | EP | EP |
| 19 | D | D | O | RD | D | RD | RD | FL | FG | RD | FL | FG |
| 20 | RD | FL | FL | RD | FL | FG | RD | EP | EP | RD | EP | RI |
| 21 | RD | D | B | RD | FL | O | RD | FL | FG | RI | O | RR |
| 22 | RD | EP | O | D | EP | B | RD | EP | O | RD | FL | FG |
| 23 | RD | D | EP | RD | EP | EP | RD | FL | FL | RD | EP | RI |
| 24 | EP | EP | EP | D | D | O | FL | FL | FL | RD | FL | FL |
| 25 | RD | O | RR | FL | FL | FL | RD | EP | RI | |||
| 26 | FL | FL | FG | FL | FL | FG | RD | O | O | |||
| 27 | D | EP | EP | RD | FL | FL | ||||||
| 28 | RD | D | RI | RD | EP | EP | ||||||
| 19 | 2 | 2 | 24 | 9 | 7 | 28 | 18 | 15 | 26 | 16 | 15 | |
4.1. NIVEL DE ÉXITO
En la tabla 3 se observa que 57% de las respuestas son correctas y que el nivel de éxito incrementa al aumentar el curso y disminuye al aumentar la complejidad de las cuestiones.
Tabla 3 Nivel de éxito
| Curso | Alumnos | Cuestión 1 | Cuestión 2 | Cuestión 3 | Total |
| 3° | 24 | 19 | 2 | 2 | 23(32%) |
| 4° | 28 | 24 | 9 | 7 | 40(48%) |
| 5° | 28 | 28 | 18 | 15 | 61(73%) |
| 6° | 26 | 26 | 16 | 15 | 57(73%) |
| Total | 106 | 97(92%) | 45(42%) | 39(37%) | 181(57%) |
32% de las respuestas de 3º curso son correctas, 48% de las respuestas de 4º son correctas y en 5º y 6º las respuestas correctas ascienden hasta 73%. Por otra parte, 92% de las respuestas a la generalización cercana son correctas, mientras que en la generalización lejana y en la regla general las respuestas correctas descienden al 45 y 37% respectivamente.
4.2. GRADOS DE DESARROLLO
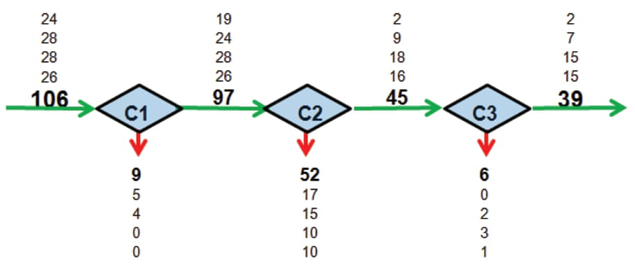
En el diagrama de flujo de la figura 3 se observa que las tres cuestiones están ordenadas por complejidad, de forma que no hay saltos entre cuestiones. De los 106 alumnos 97 realizaron correctamente la generalización cercana, de ellos 45 realizaron correctamente la generalización lejana y de estos expresaron correctamente la regla general.
Todos los estudiantes que expresaron la regla, habían realizado previamente la generalización lejana, y todos los que habían realizado la generalización lejana también habían conseguido la generalización cercana. Esto nos permite establecer cuatro grados o estadios de desarrollo bien diferenciados: en el grado cero estarían los 9 alumnos que no resuelven bien la primera cuestión; en el grado 1, los 52 que solo resuelven la generalización cercana; en el grado 2 los 6 que resuelven bien las dos generalizaciones; y en el grado 3, los 39 que resuelven correctamente las tres cuestiones (tabla 4).
Tabla 4 Nivel de éxito
| Curso | Grado 0 | Grado 1 | Grado 2 | Grado 3 |
| 3° | 5 | 17 | 0 | 2 |
| 4° | 4 | 15 | 2 | 7 |
| 5° | 0 | 10 | 3 | 15 |
| 6° | 0 | 10 | 1 | 15 |
| Total | 9(8%) | 52(49%) | 6(6%) | 39(37%) |
De esta manera 92% de los estudiantes son capaces de realizar algún tipo de generalización y 37% son capaces de completar todo el proceso de generalización.
4.3. UTILIZACIÓN DE ESTRATEGIAS
En la tabla 5 se muestran las estrategias usadas por los alumnos de cada curso en cada una de las tres cuestiones y entre paréntesis las respuestas correctas en cada caso.
Tabla 5 Estrategias usadas y niveles de éxito, por cuestiones y cursos
| Cuestión | Curso | D | EA | EF | EP | O | B | Total | |||
| RD | RI | RR | FL | FG | |||||||
| C1 | 3° | 2(1) | 17(17) | 1(1) | 4(0) | 24(19) | |||||
| 4° | 5(4) | 19(18) | 1(1) | 1(1) | 2(0) | 28(24) | |||||
| 5° | 24(24) | 4(4) | 28(28) | ||||||||
| 6° | 20(20) | 2(2) | 4(4) | 26(26) | |||||||
| Total | 7(5) | 80(79) | 3(3) | 10(10) | 6(0) | 106(97) | |||||
| C2 | 3° | 9(0) | 2(2) | 12(0) | 1(0) | 24(2) | |||||
| 4° | 5(1) | 9(8) | 11(0) | 3(0) | 28(9) | ||||||
| 5° | 18(18) | 9(0) | 1(0) | 28(18) | |||||||
| 6° | 16(16) | 8(0) | 2(0) | 26(16) | |||||||
| Total | 14(1) | 45(44) | 40(0) | 7(0) | 106(45) | ||||||
| C3 | 3° | 1(0) | 1(0) | 2(2) | 9(0) | 7(0) | 4(0) | 24(2) | |||
| 4° | 1(0) | 3(1) | 2(0) | 3(3) | 3(3) | 10(0) | 5(0) | 1(0) | 28(7) | ||
| 5° | 1(0) | 6(5) | 10(10) | 8(0) | 3(0) | 28(15) | |||||
| 6° | 4(0) | 1(0) | 4(4) | 12(11) | 4(0) | 1(0) | 26(15) | ||||
| Total | 1(0) | 9(1) | 4(0) | 15(15) | 25(25) | 31(0) | 16(0) | 5(0) | 106(40) | ||
| Total | 21(6) | 81(79) | 12(4) | 4(0) | 70(69) | 25(24) | 77(0) | 23(0) | 5(0) | 318(182) | |
| 97(83) | 95(93) | ||||||||||
Las estrategias más usadas han sido las aditivas, en 97 ocasiones; las funcionales, en 95 ocasiones; y las proporcionales, en 77 ocasiones; es decir en 31, 30 y 24% respectivamente. De las estrategias aditivas, la más usada ha sido el recuento sobre el dibujo y, de las funcionales, la función local. Las estrategias con mayor nivel de éxito han sido funcionales con 98% de éxito y las aditivas con 86%, mientras que, lógicamente, el nivel de éxito de las proporcionales fue nulo.
La estrategia más usada y con mayor éxito en la generalización cercana ha sido el recuento sobre el dibujo usada en 80 ocasiones, un 75% del total, con un nivel de éxito de 99%. En la generalización lejana la estrategia más usada ha sido la funcional local, usada en 45 ocasiones, 42%, del total fue la de mayor éxito con 98%. En la expresión de la regla general la estrategia más usada ha sido la proporcional, que ha sido usada en 31 ocasiones, 29%, seguida de la función global que 25 ocasiones, 24%, y su nivel de éxito fue de 100%.
En la tabla 6 se muestran los resultados por cursos. La estrategia más usada en 3º y 4º curso ha sido la estrategia proporcional, en 25 y 23 ocasiones respectivamente, 35 y 27%; la segunda estrategia más usada, el recuento sobre el dibujo, en 17 y 20 veces, 24% en ambos cursos, y con un nivel de éxito de 100% en 3º y de 90% en 4º. En 5º y 6º curso la estrategia más usada ha sido la función local, en 28 y 24 ocasiones, 33 y 31%, con niveles de éxito de 96% y 100% respectivamente.
Tabla 6 Estrategias usadas y niveles de éxito, por cursos
| Curso | D | EA | EF | EP | O | B | Total | |||
| RD | RI | RR | FL | FG | ||||||
| 3° | 11(1) | 17(17) | 1(0) | 1(0) | 5(5) | 25(0) | 8(0) | 4(0) | 72(23) | |
| 4° | 10(5) | 20(18) | 4(2) | 2(0) | 13(12) | 2(3) | 23(0) | 8(0) | 1(0) | 84(40) |
| 5° | 24(24) | 1(0) | 28(27) | 10(10) | 17(0) | 4(0) | 84(61) | |||
| 6° | 20(20) | 6(2) | 1(0) | 24(24) | 12(11) | 12(0) | 3(0) | 78(57) | ||
| Total | 21(6) | 81(79) | 12(4) | 4(0) | 70(69) | 25(24) | 77(0) | 23(0) | 5(0) | 318(182) |
4.4. Secuencias de estrategias
Los 39 estudiantes del nivel 3, que han conseguido completar el proceso de generalización contestando correctamente las tres cuestiones, siguieron 5 secuencias de trayectorias distintas (tabla 7).
Tabla 7 Secuencias de estrategias con éxito
| Secuencias | N° | ||
| RD | FL | FG | 18 |
| RD | FL | FL | 13 |
| FL | FL | FG | 5 |
| FL | FL | FL | 2 |
| RD | D | RI | 1 |
| 39 | |||
La secuencia RD-FL-FG, es decir, recuento sobre dibujo en la generalización cercana, función local en la generalización lejana y función global en la regla general, ha sido usada por 18 de los 39 alumnos que han superado todo el proceso de generalización.
4.5. ESTUDIO DE CASOS
En el estudio de casos se ha seleccionado un estudiante de cada uno de los cuatro grados de desarrollo establecidos: A4-4º, A15-3º, A13-5º y A9-6º (Alumno Número-Curso).
El alumno 4 de 4º curso es uno de los 9 alumnos que no han sabido realizar correctamente ninguna cuestión, por lo que pertenece al grado 0. En la generalización cercana utiliza el recuento sobre el dibujo, pero no respeta la estructura espacial al dibujar las mesas separadas, ni la estructura numérica al dibujar solo 7 mesas. El alumno arrastra el error de dibujar las mesas separadas a las otras dos cuestiones que resuelve mal utilizando en ambos casos una estrategia proporcional, multiplicando por 4 el número de mesas (figura 4).
El alumno 15 de 3º curso pertenece al grado 1, pues solo realiza correctamente la generalización cercana. En la generalización cercana dibuja las mesas y cuenta correctamente las sillas, pero en la generalización lejana utiliza erróneamente la estrategia proporcional, dividiendo entre 2 el número de mesas y como regla general dice que “se pueden sentar niños”, que, aunque siendo verdad, no sirve para hallar el número de sillas (figura 5).
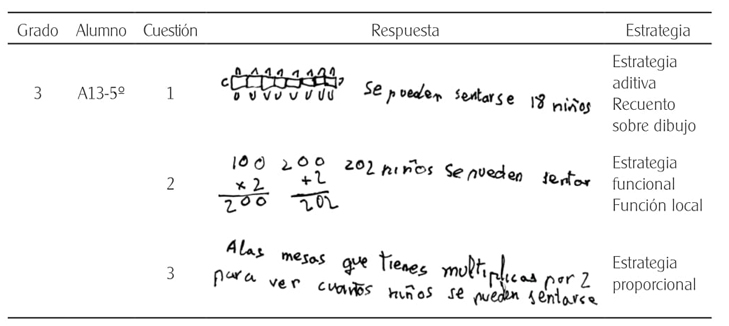
El alumno 13 de 5º curso resuelve bien las dos primeras cuestiones: la generalización cercana con un recuento sobre el dibujo y la generalización lejana usando una función local, f(100) = 100·2 + 2, al multiplicar las 100 mesas por 2 y sumar después las dos mesas de los extremos.
Sin embargo, no es capaz de expresar bien la regla general pues aunque multiplica por 2 el número de mesas, se le olvida sumar las dos de los extremos (figura 6).
El alumno 9 de 6º curso pertenece al grado 3, pues es capaz de completar todo el proceso de generalización. Las respuestas son muy parecidas al alumno anterior, pero ahora sí expresa bien la regla general, utilizando una función global, f(n) = 2n + 2, de forma verbal al escribir “primero multiplicamos por 2 el número de mesas y después lo sumamos más 2” (figura 7).
5. CONCLUSIONES
El objetivo de este trabajo fue analizar las respuestas de alumnos de primaria a un problema de generalización de patrones, estudiando los niveles de éxito, los grados de desarrollo y las estrategias usadas por 106 alumnos de Educación Primaria.
A partir del análisis de resultados se han extraído las siguientes conclusiones:
- Los alumnos responden correctamente a más de la mitad de las cuestiones y el éxito aumenta al aumentar el curso y disminuye al aumentar la complejidad de las cuestiones.
- Casi todos los alumnos son capaces de realizar alguna tarea de generalización y más de la mitad de los alumnos de 5º y 6º de primaria son capaces de completar el proceso de generalización de patrones, lo que confirma investigaciones anteriores (Mason, 1999; Socas, 2011; Carraher et al., 2003).
- Las cuestiones de generalización de patrones están interrelacionadas y jerarquizadas, de tal forma que para expresar la regla general se requiere realizar previamente la generalización lejana y para realizar la generalización lejana se requiere realizar previamente la generalización cercana identificando el patrón de crecimiento (Radford, 2008).
- La jerarquización de las tres cuestiones de la generalización de patrones permite establecer fácilmente grados de desarrollo que facultan definir los estadios de una trayectoria de aprendizaje en el proceso de generalización de patrones (Zapatera, 2018).
- Las estrategias más usadas en los cursos inferiores de Educación Primaria son las aditivas, especialmente el recuento sobre el dibujo, y en los cursos superiores las funcionales, especialmente la función local.
- Las estrategias más usadas y con mayor éxito en la generalización cercana son las aditivas, especialmente, el recuento sobre el dibujo, y en la generalización lejana y en la regla general, son las funcionales, especialmente la función local en la generalización lejana y la global en regla general.
- Las estrategias con un mayor nivel de éxito son las estrategias funcionales con 98%, seguidas de las aditivas con un 86%.
- La secuencia RD-FL-FG, es decir, recuento sobre dibujo en la generalización cercana, función local en la generalización lejana y función global en la regla general es la secuencia que proporciona mayor éxito en el proceso de generalización.
- Un aspecto importante en el desarrollo del proceso de generalización la flexibilidad, entendida como habilidad para modificar la estrategia de resolución de un problema cuando se modifica la demanda de la tarea (Krems, 1995) es un aspecto importante en el desarrollo de la generalización de patrones (Callejo y Zapatera, 2014).











 nueva página del texto (beta)
nueva página del texto (beta)