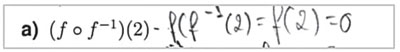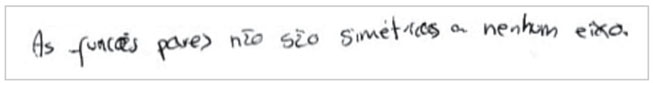1. INTRODUÇÃO

O conceito de função, para além de ser um dos mais importantes da Matemá-tica (^{Elia et al., 2007}; ^{Viseu et al., 2019}), não se restringe a esta disciplina, visto que aparece diariamente no quotidiano em diversas situações, como, por exemplo, num jornal, numa revista ou num artigo científico. Nos programas de Matemática em Portugal, este conceito é estudado pela primeira vez no 7.º ano de escolaridade⁵, o que serve de pré-requisito ao estudo de funções nos anos escolares subsequentes. No ensino de funções emergem diferentes representa-ções (algébrica, gráfica, tabular e numérica) que têm por finalidade promover a compreensão dos alunos (^{Amaya et al., 2016}; ^{Rocha, 2020}a), relativamente a um conceito em que não é possível aceder diretamente aos objetos (^{Duval, 2006}). E este é um aspeto central quando se pretende instituir nos processos de apren-dizagem a aquisição do significado dos tópicos em estudo (^{Rocha, 2016}). Entre as representações de funções evidencia-se a representação gráfica pela força que adquire nas mais variadas situações. Exemplo disso é a expressão ‘uma imagem vale mais do que mil palavras’, a que muitas vezes recorremos para evidenciar o poder da comunicação de uma ideia através de uma imagem. Assim, a representação gráfica, no papel de imagem, é um meio para estabelecer definições e propriedades, tornando-as mais claras para os alunos. Segundo o ^{NCTM (2007)}, entre as diferentes representações, “os gráficos transmitem certos tipos de informação visual, enquanto as expressões simbólicas poderão ser mais facilmente manipuladas, analisadas e transformadas” (p. 422). Apesar do racio-cínio matemático ser por excelência um raciocínio hipotético-dedutivo, também o raciocínio indutivo desempenha um papel importante na aprendizagem da matemática, como, por exemplo, na formulação de conjeturas. A observação de representações gráficas permite a formulação de conjeturas e a partir destas podem-se estabelecer conexões com os conceitos matemáticos formais. São vários os estudos que abordam a representação gráfica como instrumento poten-ciador da aprendizagem de conteúdos matemáticos, como é exemplo o estudo realizado por ^{Ferrini-Mundy e Lauten (1994)}, para quem “a representação gráfica de uma função oferece uma rica oportunidade para a exploração de relações em sala de aula” (p. 118). ^{Consciência e Oliveira (2011)} consideram que a representação gráfica é “fundamental para a compreensão de noções associadas ao conceito de função e a chave para a resolução de problemas, permitindo inclusive que os alunos possam resolver problemas antes de possuírem os conhecimentos algébricos necessários para o fazer” (p. 1).

Apesar de as funções constituírem um dos mais importantes temas no ensino da Matemática, é também um tema onde os alunos apresentam dificuldades, que não se restringem a procedimentos algébricos. A realização de representações gráficas pode ser vista como uma das atividades mais críticas da Matemática (^{Leinhardt et al., 1990}), uma vez que os alunos têm dificuldade na interpretação e na construção de gráficos de funções (^{Berg y Phillips, 1994}; ^{Rocha, 2020}b). O objetivo deste estudo não é dar exclusividade à representação gráfica na aprendizagem de funções, mas utilizá-la numa abordagem que permita “esclarecer métodos algébricos” (^{Hector, 1992}, p. 133). Em consonância com ^{Rocha (2016)}, reconhecemos a importância da integração das diferentes representações na aprendizagem. Com efeito, o uso exclusivo da representação gráfica poderia ser prejudicial para a aprendizagem dos alunos uma vez que os mesmos “sentem dificuldades ao trabalhar com as funções, em parte devido à necessidade de coordenar múltiplas representações” (^{Elia et al., 2007}). ^{Friedlander e Tabach (2001)} destacam que o uso das diferentes representações tem o potencial de tornar o processo de aprendizagem da Álgebra significativo e eficaz. A abordagem gráfica, articulada com a analítica, pode ser bastante benéfica porque “se os alunos resolverem problemas visualmente, eles têm uma compre-ensão mais profunda do que se os resolvessem apenas de um modo analítico” (^{Ferrini-Mundy y Lauten, 1994, p. 118}). Para estes autores, “pensar visualmente pode ser extremamente útil em muitos contextos relacionados com o Cálculo, e atividades que promovam e encorajem soluções visuais podem ajudar na com-preensão dos alunos” (p. 118). Recorrer a abordagens gráficas consiste em “não substituir uma abordagem algébrica, mas sim esclarecê-la” (^{Hector, 1992, p. 133}), promovendo “o pensamento visual dos alunos, incentivando-os a pensar primeiro numa estrutura visual e, depois, numa analítica” (^{Ferrini-Mundy y Lauten, 1994, p. 118}). E, para além disso, perceber que são possíveis diferentes represen-tações gráficas de funções e compreendê-las, pode igualmente constituir um importante contributo para o desenvolvimento de uma maior compreensão dos conceitos subjacentes (^{Rocha, 2020b}). Tendo como referência tais pressupostos, este trabalho procura analisar o contributo das representações gráficas na aprendizagem de tópicos de funções por alunos do 10.º ano de escolaridade, mais concretamente na aprendizagem da noção de função inversa e da paridade de uma função. Pretende ainda dar atenção às dificuldades dos alunos associadas ao uso desta representação.

2. AS CONEXÕES ENTRE DIFERENTES REPRESENTAÇÕES

As representações matemáticas relacionam-se com o “raciocínio matemático devido ao seu importante papel no ensino e na aprendizagem da Matemática e, consequentemente, no desenvolvimento e compreensão dos processos de raciocínio dos alunos” (^{Henriques y Ponte, 2014, p. 277}). ^{Ponte et al. (1998)} consideram que o “raciocínio matemático exige o trabalho intensivo com repre-sentações externas, sejam elas símbolos matemáticos, diagramas, gráficos” (p. 173). O uso destas representações facilita o processo de comunicação, se houver interligação da manipulação simbólica com os significados que associamos aos conceitos. Os conceitos matemáticos são também trabalhados mentalmente, utilizando as representações internas dos conceitos (^{Ponte et al., 1998}). Para estes autores, as “capacidades de representar os conceitos matemáticos e de relacionar entre si as diversas representações de um mesmo conceito estão associadas ao pensamento matemático avançado” (p. 173). Contudo, os alunos têm dificuldade em estabelecer conexões entre diferentes representações de funções, na interpretação de gráficos e na manipulação de símbolos (^{Elia et al., 2007}). Segundo estes autores e segundo ^{Gagatsis e Elia (2005)}, cada representação oferece informação sobre aspetos particulares do conceito em estudo sem o descrever completamente. ^{Friedlander e Tabach (2001)} advogam que as diver-sas representações de funções (a verbal, a numérica, a gráfica e a algébrica) possuem vantagens e desvantagens:

Cada uma das representações de funções destaca diferentes particularidades, que em conjunto contribuem para a formulação do conceito global de função, o que realça o papel da conversão entre diferentes representações na compreensão do conceito de função (^{Duval, 2017}).

Partindo do pressuposto de que muitas das dificuldades que os alunos sentem a trabalhar com funções se deve à necessidade de coordenar múltiplas representações, ^{Elia et al. (2007)} realizaram um estudo para investigar as aptidões dos alunos na elaboração da definição de função, a capacidade de reconhecerem funções em diversas representações e a capacidade de resolverem problemas envolvendo a conexão de uma forma de representação para outra. Os resultados revelam dificuldades dos alunos em dar uma definição adequada do conceito de função e em resolver problemas envolvendo a transição entre representações. Neste estudo, também foi detetada uma estreita relação entre os alunos que apresentavam a definição de função corretamente e os que reconheciam funções de entre as relações matemáticas representadas grafica-mente, o que levou os autores a concluir que os alunos eram mais propensos a aplicar a sua definição de função numa representação gráfica do que noutro tipo de representação. Por seu turno, ^{Viseu et al. (2019)} concluíram que o reconhecimento de funções ocorria com maior facilidade a partir da representação tabular do que a partir da representação gráfica ou algébrica. Para ^{Elia et al. (2007)}, os alunos tendem a ver nas diferentes representações de uma função objetos matemáticos distintos e autónomos e não diferentes modos de expressar o mesmo objeto. Segundo os autores, a transição entre representações não é trabalhada adequadamente, tal como também é sugerido por ^{Rocha (2016)}, existindo uma ‘compartimentação’ das representações, o que resulta de cada representação ser trabalhada isoladamente sem serem estabelecidas conexões entre os diversos tipos de representação. As múltiplas representações têm três funções chave: (a) complementar; (b) restringir; e (c) construir (^{Ainsworth, 2006}). De entre todas as representações há uma que tem especial destaque neste estudo, a representação gráfica.

3. A REPRESENTAÇÃO GRÁFICA

A representação gráfica de funções traduz uma atividade relevante na educação matemática dos alunos (^{Hattikudur et al., 2012}). O destaque das representações gráficas no ensino e na aprendizagem tem ocorrido ao longo dos últimos anos, tendo sofrido um incremento considerável a partir do momento em que a tecnologia proporcionou um fácil acesso a estas (^{Rocha, 2020}b), o que fez aumentar o número de tarefas com este tipo de representação na sala de aula e nos manuais escolares. Atendendo à importância que sempre foi reconhecida a este tipo de representação, ^{Leinhardt et al. (1990)} estabeleceram uma categorização para as tarefas com gráficos. Classificaram tais tarefas por dois tipos de ação -a interpretação e a construção-, e transversalmente por quatro tipos de tare-fas -a previsão, a classificação, a conversão e a escala.

A interpretação refere-se à ação pela qual um aluno dá sentido ou significado a partir de um dado gráfico ou parte de um gráfico. A interpretação pode ser global, referindo-se às propriedades de todo o gráfico ou parte dele, ou pode ser local, referindo-se às propriedades de um ponto do gráfico. A construção refere-se às atividades em que os alunos constroem um gráfico a partir de uma equação ou de pontos dados, ou reciprocamente, ou seja, constroem uma relação algébrica que representa um determinado gráfico. A construção é diferente da interpretação. Enquanto a interpretação requer a reação a um dado gráfico, a construção requer que os alunos gerem novos gráficos ou equações que não são dadas.

As tarefas de previsão exigem aos alunos que conjeturem a partir de um gráfico onde outros pontos do gráfico devem estar localizados ou como outras partes do gráfico devem ser. As tarefas de previsão envolvem necessariamente a construção do gráfico ou da parte ausente do gráfico. As tarefas de classificação referem-se a situações em que os alunos têm de decidir se um dado gráfico representa ou não uma função, se pertencem a um tipo especial de funções ou se têm determinada característica ou propriedade. As tarefas de conversão exigem que os alunos reconheçam a mesma função em diferentes representações, que construam um gráfico a partir de uma equação ou de um conjunto de pares ordenados, e que construam uma expressão algébrica a partir de um gráfico. As tarefas de conversão podem ser de construção ou de interpretação. As tarefas de escala exigem que os alunos considerem os eixos, as suas escalas e unidades que os marcam, e estão associadas a situações em que se utilizam tecnologias gráficas. Também este tipo de tarefa pode ser de construção ou de interpretação. Estes tipos de tarefa estão associados a interpretação e a constru-ção de gráficos, mas estes dois tipos de ação acarretam por vezes algumas dificuldades para os alunos. Tais dificuldades podem dever-se, segundo ^{Leinhardt et al. (1990)}, à tendência dos alunos, quando analisam gráficos, de restringirem o seu foco a um ponto ou a um grupo de pontos em vez de realizarem uma interpretação global do gráfico. Este foco pontual é devido essencialmente ao tipo de ensino a que estão sujeitos no início do estudo de funções, no qual têm de representar gráficos a partir de uma tabela de pares ordenados. Assim, os alunos utilizam os gráficos como usam as tabelas, para procurar informações específicas. No estudo realizado por ^{Leinhardt et al. (1990)} foram identificadas algumas dificuldades que os alunos têm na interpretação e construção de gráficos, que foram agrupadas em três categorias principais: (a) confusão entre intervalo e ponto; (b) confusão entre declive e altura; e (c) interpretações icónicas.

^{Mevarech e Kramarsky (1997)} realizaram um estudo onde foram identificadas três conceções alternativas dos alunos na construção de gráficos: (a) a construção de um gráfico inteiro como um único ponto; (b) a construção de um conjunto de gráficos, em que cada um era representativo de um dos fatores relevantes apresentados pelos dados; (c) a conservação da forma de uma função crescente sob todas as condições. Para além destes erros ocorreram outros em menor número associados a ideias estereotipadas de gráficos, ou seja, constru-íram gráficos com linhas que subiam e desciam sem exibir qualquer ligação com a narrativa e construíram um gráfico por setas ou escadas em vez de linhas.

^{Leinhardt et al. (1990)} também identificaram conceções erradas e dificulda-des de alguns alunos. Para além das já referidas, os alunos têm especial tendência em diversas situações de recorrer à linearidade para representar gráficos. Uma das grandes dificuldades apresentadas pelos alunos consistiu em decidir se um gráfico é ou deve ser representado de maneira contínua ou discreta: “os alunos mostraram-se confusos sobre o significado que pode ser atribuído a uma linha ininterrupta de um gráfico contínuo” (p. 34). Segundo ^{Markovits et al. (1986)} quando os alunos eram solicitados a criar exemplos de gráficos de funções que passariam por dois pontos dados, produziam principalmente gráficos lineares. Quando os alunos eram questionados se outros gráficos poderiam passar pelos dois pontos, a maioria indicou com uma certeza considerável que o gráfico que tinham desenhado era o único gráfico que passaria pelos pontos. Segundo os autores, o raciocínio dos alunos era de que apenas uma linha poderia passar por quaisquer dois pontos, sugerindo que estes estavam a generalizar a propriedade de funções lineares, isto é, que uma reta é determinada por dois pontos.

Num outro estudo realizado por ^{Markovits et al. (1988)}, os alunos expressa-ram dificuldades com os termos imagem, imagem inversa, par ordenado, domínio, contradomínio e conjunto de chegada. Segundo os autores, estas dificuldades resultam em outras, como em localizar imagens e imagens inversas nos eixos das representações gráficas, identificar imagens e pares ordenados em funções definidas pela sua expressão algébrica, distinguir contradomínio e conjunto de chegada, e ignorar o domínio e o conjunto de chegada das funções. Para ^{Markovits et al. (1988)}, os alunos não estabelecem conexões entre as componentes da definição verbal de uma função e as componentes correspon-dentes na representação gráfica. Os alunos também apresentam dificuldades com alguns tipos de funções, tais como funções constantes, funções represen-tadas por gráficos descontínuos e funções definidas por ramos. Os autores concluem que é mais fácil para os alunos trabalharem com funções represen-tadas graficamente do que com funções representadas algebricamente, visto que a “representação gráfica é mais visual” (p. 57) e, por isso, sugerem que deve ser feito mais trabalho no desenvolvimento inicial de conceitos relacionados com funções de uma forma gráfica. Há mesmo quem considere que o estudo com gráficos deve ser iniciado relativamente cedo, no ensino primário, antes mesmo do ensino dos números negativos, e que deve ser usado na resolução de problemas (^{Demana et al., 1993}). O trabalho com gráficos é de enorme importância no estudo de tópicos sobre funções, partindo do pressuposto de que os alunos quando trabalham com “diferentes tipos de funções e produzem gráficos de cada tipo, eles familiarizam-se com a relação entre regras de funções e gráficos e aprendem a classificá-las” (^{Hector, 1992, p. 132}).

4. METODOLOGIA

Com este estudo pretende-se analisar o contributo da representação gráfica na aprendizagem da noção de função inversa e da paridade de uma função por alunos do 10.º ano de escolaridade e identificar dificuldades na exploração dessa representação. Atendendo a este objetivo, um dos autores realizou, no âmbito do seu estágio pedagógico, no último ano do mestrado de formação de professores, uma experiência de ensino baseada na utilização de tarefas matemáticas que apelavam ao uso da representação gráfica de funções, com realce neste trabalho para o estudo da função inversa e da paridade de funções. Esta experiência de ensino decorreu ao longo de treze aulas e incorporou tarefas matemáticas, das quais selecionamos seis. A resolução de cada uma das tarefas teve características do ensino exploratório iniciando com a introdução da tarefa (momento de leitura, interpretação da informação e clarificação de significados), seguindo-se a resolução pelos alunos e a sua discussão coletiva. A ausência de alunos em algumas das aulas faz com que exista uma diferença do número de dados recolhidos nas tarefas analisadas.

A turma onde se realizou esta experiência de ensino era composta por 26 alunos, 11 do sexo masculino e 15 do sexo feminino, com idades de 15 ou 16 anos. Tratava-se de uma turma composta por alunos bem-comportados, mas pouco participativos em vários momentos das aulas. A turma era diversificada em termos de desempenho, pois tinha alguns alunos com bastantes conhecimentos e bom raciocínio e outros com diversas dificuldades de aprendizagem, algumas delas resultantes do seu histórico estudantil. Esta diversificação justifica os diferentes ritmos de trabalho na resolução das diversas tarefas propostas.

Atendendo à natureza do objetivo delineado, adotámos uma abordagem qualitativa e interpretativa com o intuito de compreender a atividade matemáti-ca dos alunos na resolução das tarefas propostas em contexto de sala de aula (^{Bogdan y Biklen, 1994}). Com esta finalidade, os dados foram recolhidos através das resoluções das tarefas propostas pelos alunos no estudo de tópicos de funções antes da sua discussão no grupo turma. A análise de dados assentou na análise do conteúdo dessas resoluções, sendo traduzida pelas frequências dos tipos de resposta consideradas corretas (C), parcialmente corretas (PC), incorretas (I) e não respondidas (NR), tendo como referência a categorização de ^{Leinhardt et al. (1990)} para a classificação das tarefas - previsão, classificação e conversão (tarefas de escala não serão abordadas neste artigo) - e das res-petivas ações -interpretação e construção. Consideramos que tais tipos de res-posta traduzem a capacidade do aluno em se apropriar, na representação gráfica, dos tópicos em estudo através da compreensão das propriedades que os definem.

5. APRESENTAÇÃO DOS RESULTADOS

Na explicitação da experiência de ensino com recurso à representação gráfica no estudo de tópicos de funções, incidimos no estudo da função inversa, e da função par e/ou ímpar, pois na exploração destes tópicos as orientações metodológicas do programa escolar português dão ênfase a este tipo de representação.

5.1. Função Inversa

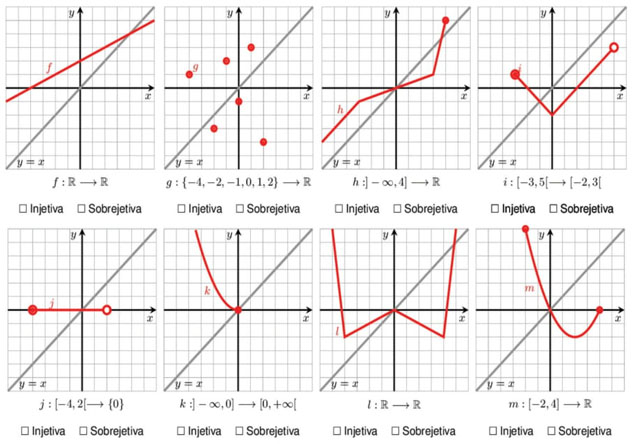
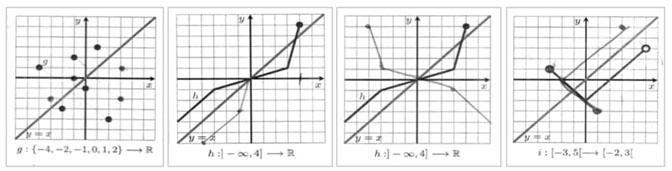
No estudo do conceito de função inversa, com o intuito de estabelecerem a definição deste conceito, tendo como referência os conhecimentos adquiridos no estudo da injetividade de uma função, os alunos começaram por resolver a seguinte tarefa:

Tarefa 1. Considera os seguintes gráficos cartesianos de funções.
Classifica cada uma das funções quanto à injetividade e sobrejetividade. Esboça a reflexão axial de eixo y = x do gráfico de cada uma das funções representadas. Quais das reflexões representam funções? Que característica tem de possuir uma função para que a reflexão axial do seu gráfico segundo o eixo y= xrepresente uma função?

A tarefa é constituída por uma sequência lógica de questões criadas para os alunos descobrirem que uma função só admite inversa se for injetiva. As questões foram apresentadas aos alunos gradualmente, visto que não tinham acesso às questões seguintes antes de responder à anterior. Na resolução desta tarefa, os alunos começaram por rever os conceitos de função injetiva e função sobrejetiva, importantes na construção do conceito de função inversa de uma dada função. Globalmente, os alunos apresentaram 75% de respostas corretas e 24% de respostas parcialmente corretas, sendo apenas consideradas 1% das respostas como incorretas. Após a revisão destas noções, os alunos esboçaram a reflexão axial de eixo y = x de cada um dos gráficos das funções representadas na Tarefa 1. Na Tabela 1 são apresentados os resultados das respostas dos alunos à alínea 2 da Tarefa 1.

Tabela 1 Frequência dos diferentes tipos de resposta dos alunos à alínea 2 da Tarefa 1 (n = 26) 

Ação	Tarefa	Funções	Tipos de Resposta
			C	PC	I	NR
Construção	Previsão	f	24	-	-	2
		g	10	-	13	3
		h	15	-	7	4
		i	10	-	5	11
		j	7	-	6	13
		k	8	-	8	10
		l	6	-	5	15
		m	4	-	5	17

Relativamente à função f, a maioria dos alunos representou corretamente a reflexão do gráfico desta função segundo o eixo y = x. Nas alíneas seguintes foram apresentadas várias respostas incorretas que se deveram a vários erros, como, por exemplo, os alunos produzirem incorretamente parte ou a totalidade da reflexão do gráfico da função, realizarem apenas a reflexão de parte do gráfico da função, realizarem a reflexão segundo um eixo que não o pedido na questão apresentada, realizarem a reflexão de partes do gráfico que não existem ou realizarem incorretamente a reflexão de pontos abertos (não preenchidos) e de pontos fechados (preenchidos) do gráfico da função (Figura 1).

Figura 1 Respostas incorretas dos alunos A25, A25, A23 e A9 à alínea 2 da Tarefa 1  

Durante a aula foram respondidas e corrigidas as alíneas seguintes e foi introduzido o conceito de função inversa a partir das intervenções dos alunos. Após isso, foram introduzidas novas ideias relacionadas com esta temática através da Tarefa 2. A partir de conjeturas, os alunos adquiriram conhecimentos relativos à inversa da função inversa, à composta de uma função com a sua inversa e à composta da inversa com a função.

Tarefa 2. Considera o seguinte gráfico cartesiano da função f:  [-6,6]  →  [-4,4].
1. A função 𝑓 admite função inversa? Se sim, representa graficamente a função inversa de 𝑓. 2. Representa graficamente a inversa da função inversa de 𝑓. 3. Considerando que cada quadrícula representa uma unidade, determina: a) (f∘ f-1)(2) c) (f∘f-1)(-4) b) (f-1∘f)(3) d)(f-1∘ f)(-1)

Esta tarefa foi resolvida pelos alunos individualmente, sendo corrigida e analisadas as conclusões retiradas no grupo turma. Na Tabela 2 apresentam-se os resultados das respostas dos alunos à alínea 1 da Tarefa 2.

Tabela 2 Frequência dos diferentes tipos de resposta dos alunos à alínea 1 da Tarefa 2  

Ação	Tarefa	Tipos de Resposta
		C	PC	I	NR
Construção	Previsão	24	-	1	1

Cerca de 92% dos alunos concluíram que a função admite inversa e repre-sentaram corretamente esta função produzindo a reflexão do gráfico da função segundo o eixo y = x. Houve apenas um aluno que não respondeu e uma resposta incorreta à alínea 1 da Tarefa 2 (Figura 2).

Figura 2 Resposta incorreta do aluno A26 à alínea 1 da Tarefa 2  

Seguiu-se a representação da inversa da função representada na alínea anterior. Esta questão fundamenta-se pela oportunidade de os alunos conjeturarem que a inversa da função inversa de uma dada função é a própria função. Na Tabela 3 são apresentados os resultados das respostas dos alunos à alínea 2 da Tarefa 2.

Tabela 3 Frequência dos diferentes tipos de resposta dos alunos à alínea 2 da Tarefa 2 

Ação	Tarefa	Tipos de Resposta
		C	PC	I	NR
Construção	Previsão Definição	24	-	-	2

Os alunos que responderam corretamente à alínea 1 da Tarefa 2 foram capazes de responder à alínea 2. Antes da resolução das tarefas seguintes, foi relembrado o conceito de função identidade, pois a tarefa seguinte dá oportunidade aos alunos de conjeturarem que tanto a composta de uma função com a sua inversa como a composta da inversa de uma função com a função são a função identidade. Na Tabela 4 são apresentados os resultados das respostas dos alunos à alínea 3 da Tarefa 2.

Tabela 4 Frequência dos diferentes tipos de resposta dos alunos à alínea 3 da Tarefa 2  

Ação	Tarefa	Alíneas	Tipos de Resposta
			C	PC	I	NR
Interpretação	Definição	(a)	17	3	2	4
		(b)	15	6	1	4
		(c)	12	5	2	7
		(d)	12	3	1	10

As duas primeiras alíneas foram respondidas corretamente pela maioria dos alunos, o que já não acontece com as seguintes, havendo nestas alíneas um maior número de alunos que não respondeu.

As respostas parcialmente corretas deveram-se à determinação indevida da imagem pela segunda função que compõe a composta, como revelam as res-postas às alíneas (a) e (d) apresentadas pelo aluno A25 e as respostas às alíneas (b) e (c) apresentadas pelo aluno A8 na Figura 3.

Figura 3 Respostas parcialmente corretas às alíneas 3a) e d) da Tarefa 2 do aluno A25 e às alíneas 3b) e c) do aluno A8 

As respostas incorretas deveram-se à errada determinação da primeira ou de ambas as imagens pelas funções que compõem a composta, tal como se mos-tra pela resposta dada à alínea (a) pelo aluno A20 na Figura 4.

Figura 4 Resposta incorreta do aluno A20 à alínea 3 da Tarefa 2  

A correção desta tarefa serviu para esclarecer que a imagem de um objeto pela composta de uma função com a sua inversa ou vice-versa é o próprio objeto, ou seja, que esta é igual à função identidade (nos respetivos domínios).

5.2. Função Par e Função Ímpar

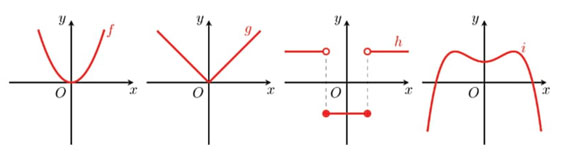
O estudo do conceito de função par e de função ímpar envolveu os alunos na formulação das suas definições através da resolução de tarefas que ilustram exemplos positivos e negativos destes conceitos, como exemplifica a Tarefa 3.

Tarefa 3. As funções representadas pelos seguintes gráficos são pares. Os gráficos seguintes representam funções que não são pares. Que característica distingues nos gráficos das funções pares que não se verifica nos gráficos das funções que não são pares?

O objetivo da Tarefa 3 é de utilizar a característica gráfica das funções pares identificada pelos alunos para definir simbolicamente o conceito de função par. A análise das respostas dos alunos mostrou que a maior parte não respondeu corretamente à tarefa (Tabela 5).

Tabela 5 Frequência dos diferentes tipos de resposta dos alunos à Tarefa 3 (n= 26) 

Ação	Tipo de Tarefa	Tipos de Resposta
		P	PC	I	NR
Interpretação	Definição	10	11	3	2

As respostas corretas dadas pelos alunos evidenciaram duas das características das funções pares: a simetria existente no gráfico deste tipo de funções relativamente ao eixo e a igualdade existente entre as imagens de objetos simétricos. Na maioria das resoluções apresentadas pelos alunos foi identificada uma destas características. Porém, alguns alunos apresentam erros de linguagem nas suas respostas, razão pela qual estas foram consideradas parcialmente corretas (42%), como foi o caso dos alunos A6 e A3 (Figura 5).

Figura 5 Resposta parcialmente correta dos alunos A6 e A3, respetivamente, à Tarefa 3  

Para além da falta de rigor de linguagem matemática, há alunos que apresentam dificuldades em distinguir os conceitos simetria e reflexão, como, por exemplo, o aluno A15 (Figura 6).

Figura 6 Resposta incorreta do aluno A15 à Tarefa 3  

A reflexão relativamente ao eixo 𝑂𝑦 pode ser utilizada como estratégia para verificar se uma função é par. Contudo, a característica que o gráfico de uma função par possui é a simetria relativamente ao eixo 𝑂𝑦. Para além destas respostas incorretas, há um aluno que não identifica nenhuma simetria nos gráficos das funções pares, como retrata a resolução da Figura 7.

Figura 7 Resposta incorreta do aluno A21 à Tarefa 3  

Posteriormente, foi discutido e definido o conceito de função par com o grupo turma. Desta discussão, resultou por parte dos alunos a possibilidade de as funções pares não serem injetivas. Após a concretização da tarefa e da elaboração da definição de função par com o grupo turma, os alunos elaboraram alguns exemplos de funções pares cumprindo, caso fosse possível, os critérios contemplados nas seguintes questões:

Tarefa 4: Responde às seguintes questões: Questão 1. Uma função de domínio R representada graficamente por uma reta pode representar uma função par? Dá exemplos? Questão 2. Uma função de domínio R representada graficamente por uma parábola pode representar uma função par? Dá exemplos?

Tabela 6 Frequência dos diferentes tipos de resposta dos alunos às Questões 1 e 2 da Tarefa 4 (n = 26) 

Ação	Tarefa		Alíneas	Tipos de Resposta
				C	PC	I	NR
Construção	Previsão	Reta	Função Par	14	4	8	-
			Função Não Par	14	6	3	3
		Parábola	Função Par	24	2	-	3
			Função Não Par	15	2	9	3

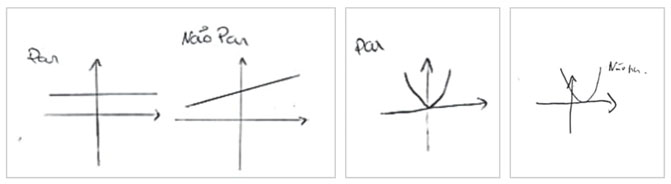
A maior parte dos alunos foi capaz de apresentar exemplos de funções pares e não pares, embora nem todos cumprissem com os critérios delineados. Relativamente às respostas parcialmente corretas, nestas duas questões deveram-se àfalta de identificação dos eixos coordenados nas respetivas representações gráficas, tal como revelam as seguintes respostas dadas por três alunos (Figura 8).

Figura 8 Respostas parcialmente corretas dos alunos A5, A17 e A20 às Questões 1 e 2 da Tarefa 4  

Quanto às respostas incorretas à Questão 1, constata-se que há alunos que apresentaram funções cujo domínio não era R (Figura 9).

Figura 9 Respostas incorretas dos alunos A3 e A19 à Questão 1 da Tarefa 4  

Na Questão 2, um aluno apresenta corretamente o gráfico de uma função par e o gráfico de uma função não par, contudo não cumpre o estipulado no enunciado, pois a função não par não é representada por uma parábola, mas sim por parte de uma parábola e, consequentemente, não cumpre o domínio proposto (Figura 10).

Figura 10 Resposta correta e resposta incorreta do aluno A11 à Questão 2 da Tarefa 4  

Após o estudo das funções pares, efetuou-se o estudo das funções ímpares seguindo uma estratégia análoga. Será omitido este estudo por não haver algo significativamente relevante comparativamente com o estudo das funções pares. De seguida foram consolidados os conhecimentos com a resolução de algumas tarefas que são analisadas seguidamente.

Tarefa 5. Indica se as seguintes funções representadas graficamente são pares, ímpares ou nem pares nem ímpares.

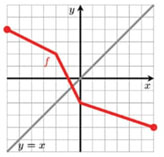
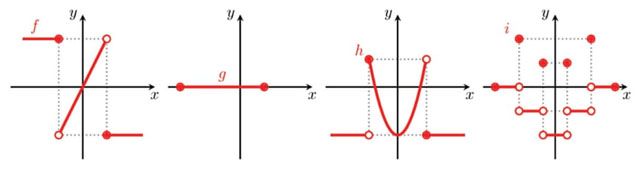
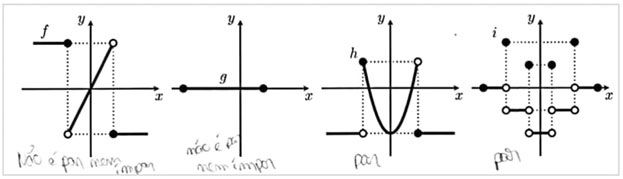
Nesta tarefa pretendia-se que os alunos, através da observação do gráfico car-tesiano da função, fossem capazes de a classificar quanto à paridade. Na Tabela 7 são apresentados os resultados das respostas dos alunos à Tarefa 5.

Tabela 7 Frequência dos diferentes tipos de resposta dos alunos à Tarefa 5 (n = 20) 

Ação	Tarefa	Funções	Tipos de Resposta
			C	PC	I	NR
Interpretação	Classificação	f	17	-	2	1
		g	19	-	-	1
		h	17	-	2	1
		i	17	-	1	2

A maioria dos alunos foi capaz de averiguar a paridade de cada uma das funções representadas graficamente na tarefa. Houve alunos que apresentaram respostas erradas, como mostra a resolução do aluno A20 na Figura 11.

Figura 11 Respostas incorretas (funções f e ℎ) do aluno A20 à Tarefa 5  

Para a análise da paridade de uma função através da sua representação gráfica é essencial o conceito de simetria (relativamente a um eixo e a um ponto). A simetria relativamente a um ponto, que está associada ao gráfico de uma função ímpar, é um conceito complexo para os alunos assimilarem e pos-sivelmente estará associado à não identificação da função como função ímpar. Por outro lado, a identificação pelo aluno da função ℎ como sendo uma função par denota a não compreensão da simbologia da bola preenchida e da bola não preenchida no gráfico de uma função.

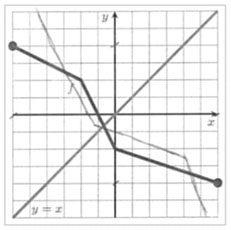
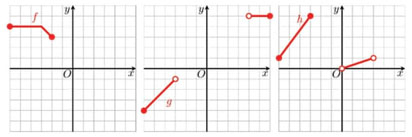
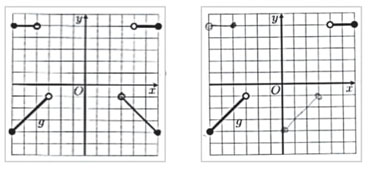
Numa outra tarefa, os alunos foram desafiados a completarem os gráficos cartesianos, sempre que possível, de modo a que as funções sejam pares.

Tarefa 6. Completa, sempre que possível, os gráficos cartesianos das funções de modo a serem pares.

Na Tabela 8 são apresentados os resultados das respostas dos alunos à Tarefa 6.

Tabela 8 Frequência dos diferentes tipos de resposta dos alunos à Tarefa 6 (n = 20) 

Ação	Tarefa	Funções	Tipos de Resposta
			C	PC	I	NR
		f	18	-	2	-
Construção	Previsão	g	2	-	18	-
		h	14	-	6	-

Na construção dos gráficos cartesianos relativos às funções e ℎ, a percentagem de alunos que responderam corretamente é elevada (90% e 70% respetivamente). As respostas incorretas dos alunos deveram-se à incorreta reflexão relativa-mente ao eixo , à reflexão de apenas parte da representação gráfica ou à escolha errada da reflexão que permite satisfazer a característica gráfica que possuem todos os gráficos cartesianos das funções pares, como ilustram as respostas dos alunos A5, A9, A10 e A19 (Figura 12).

Figura 12 Respostas incorretas dos alunos A5, A9 (função ), A10 e A19 (função ℎ) à Tarefa 6  

Na resolução da parte da tarefa relativa à função , os alunos apresentam mais dificuldades, que se devem, como ilustra a resolução do aluno A10, à construção da simetria relativamente ao eixo sem se aperceber que o gráfico cartesiano que apresenta não representa uma função. Este tipo de resposta foi apresenta-do por 85% dos alunos que realizaram esta tarefa. Na segunda resolução, o aluno A9, para além de apresentar um gráfico que não representa uma função, construiu a reflexão pretendida incorretamente (Figura 13).

Figura 13 Respostas incorretas dos alunos A10 e A9 à Tarefa 6 (função g) 

6. CONCLUSÕES

São diversos os autores que reconhecem o papel da representação gráfica na aprendizagem dos alunos (^{Hattikudur et al., 2012}; ^{Hector, 1992}; ^{Mevarech y Kramarsky, 1997}), sendo essencial a proposta de tarefas com a representação gráfica para uma melhor compreensão dos conteúdos estudados (^{Rocha, 2020}b). Este estudo ilustra precisamente a forma como a representação gráfica pode contribuir para o desenvolvimento dos conceitos por parte dos alunos. De facto,

a representação gráfica facilita o confronto entre exemplos e não exemplos, potenciando a identificação das propriedades que caracterizam os entes matemáticos em estudo. No estudo da inversa de uma função, os gráficos evidenciam as propriedades das funções injetivas e sobrejetivas e a verificação que a transformada do gráfico de uma função por reflexão segundo o eixo y = x represen-ta ou não uma função. Deste modo, torna-se mais intuitiva para os alunos a relação entre bijetividade e a existência de função inversa de uma função do que a exploração algébrica daquelas propriedades. No caso do estudo da pari-dade de uma função, a representação gráfica resulta numa abordagem eficaz por trabalhar com as simetrias axial e central, tópicos que os alunos reconhecem desde os anos iniciais. A análise e a construção de exemplos e não exemplos das condições satisfeitas por um objeto matemático permite ao aluno construir a definição desse mesmo objeto, em sintonia com o preconizado por ^{Joyce e Weil (1996)} e por ^{Leinhardt et al. (1990)}.

Na realização de tarefas que envolvem a interpretação e a construção de gráficos, alguns alunos tendem a apresentar dificuldades (^{Berg y Phillips, 1994}). Tais dificuldades devem-se, segundo ^{Elia et al. (2007)}, às dificuldades em explorar as di-ferentes representações, pois veem objetos matemáticos distintos e autónomos e não diferentes modos de expressar o mesmo objeto, existindo uma ‘compartimentação’ das representações. Cada representação é trabalhada isoladamente sem serem estabelecidas conexões entre os diversos tipos de representação (^{Elia et al., 2007}). No caso do estudo em questão, os conceitos surgiram a partir da representação gráfica e a sua formalização implica o desenvolvimento de uma articulação com outra representação. Alguns conceitos sobre funções estão associados a algumas características gráficas, como, por exemplo, o de função inversa de uma dada função, onde os alunos representaram o gráfico cartesiano da função inversa, que é obtido a partir da reflexão de eixo y = x do gráfico da função original. Alguns alunos apresentaram algumas dificuldades em produzir tais reflexões, pois, tal como sugerido por ^{Kuchemann (1981)}, a posição/inclinação do eixo de reflexão influencia as respostas dos alunos, uma vez que estes apresentam melhor desempenho quando o eixo de reflexão é vertical ou horizontal. Segundo ^{Markovits et al. (1988)}, a localização de imagens e imagens inversas a partir do gráfico cartesiano de funções é uma das dificuldades apresentadas pelos alunos no trabalho com gráficos. No presente estudo, apesar do recurso sistemático à representação grá-fica na abordagem dos conteúdos associados a conceitos sobre funções, alguns alunos não foram capazes de associar determinadas características gráficas de alguns conceitos à sua definição algébrica. Ainda assim, esta abordagem parece ter potenciado essa associação.

As tarefas que exigem que os alunos trabalhem com a calculadora gráfica colocam muitas vezes dificuldades, algumas destas associadas à escolha correta da janela de visualização (^{Rocha, 2020}b). Segundo ^{Rosa (2013)}, uma das maiores dificuldades na utilização das calculadoras gráficas pelos alunos é mesmo a definição de uma correta janela de visualização que lhe permita observar o esboço gráfico de uma função que contemple as características que a determinam. A dificuldade em identificar o domínio de uma função a partir da sua representação gráfica é uma das problemáticas identificadas nos participantes neste estudo, algo também já referido por ^{Markovits et al. (1988)}.

Uma das dificuldades dos alunos com a representação gráfica reside na definição de conceitos e no estabelecer de propriedades, uma vez que não estão habituados a serem eles os promotores da criação dos aspetos formais nas aulas de Matemática. Relativamente às dificuldades que os alunos denotam ter com a representação gráfica, ^{Eisenberg (2002)}, a partir da análise de alguns estudos, aponta para o facto de os alunos simplesmente não entenderem alguns dos gráficos que eles mesmos desenham. Para o autor, esses estudos mostram que muitos alunos nem conseguem interpretar gráficos, possivelmente por não entenderem a relação que o gráfico descreve entre as variáveis independente e dependente. O presente estudo, onde um número significativo de alunos con-seguiu desenvolver respostas corretas, sugere, contudo, que um trabalho em que os conceitos são abordados a partir da representação gráfica tem potencial para ajudar a ultrapassar essas dificuldades.