EL CERO A MODO DE INTRODUCCIÓN

Este ensayo es una edición especial y en español del artículo alemán “Die Gestalt des‚ Nichts’ in der Mathematik” (^{Reyes-Santander y Brandl, 2010}). Su versión original está en alemán y su traducción sería la figura de la “nada” en matemática y aparece como capítulo del libro Hacer nada.³ Pero ¿qué es hacer nada? ¿Qué es hacer nada en matemática? Vemos, primero que la figura de la “nada” en matemática tiene relación con los procesos de enseñar y aprender matemática. La nada y su símbolo está presente en toda la vida del estudiante en clases de matemática, aquí se presenta la nada como fuente de creación matemática y de razonamientos profundos, para ayudar a futuros docentes de diferentes áreas, a comprender que la nada puede llegar a generar existencia de conceptos e ideas, como un alimento para el pensamiento.

Comencemos con el cero desde un punto de vista histórico, sobre su nacimiento y su uso. El sistema posicional más antiguo y conocido en el mundo occidental, es el que fue desarrollado por los babilonios (alrededor del 4000 a. C.). En este sistema, una cifra por ejemplo la cifra 7, puede tomar diferentes valores según la posición en la que se encuentra. Los mayas, los indios y los chinos lograron el mismo descubrimiento, pero de forma independiente. Finalmente, los árabes nos heredaron el símbolo “0” junto con los llamados números arábigos, los cuales son esencialmente similares a los números indios.

Los indios utilizaron el cero de la misma manera que lo utilizamos nosotros hoy en día. En cambio, los mayas conocían el cero y lo ubicaban en la mitad o al final de su representación de símbolos, a pesar de esta forma de utilizar el símbolo cero, los mayas podían hacer cálculos simbólicos (^{Ifrah, 1998}). En el siglo 2 a. C. los babilonios aún no conocían el cero, según la tabla de Uruks que data de la primera dinastía babilónica (^{Ifrah, 1998, pp. 417-420}). No es conocido de manera exacta el momento en que el cero fue introducido en esta cultura. Aunque se estima que podría ser luego de la caída del imperio seléucida (312-63 a. C.), donde se comienza a utilizar un símbolo diferente a los 59 ya existentes.

El concepto de “resultado cero” para esta cultura no era asociado al símbolo y tampoco había expresiones verbales escritas como “nada” para expresar que el resultado obtenido era cero, como se muestra en la siguiente cita de ^{Ifrah (1998, pp. 423)}:

En un texto de Susa […] el escribano concluye la sustracción de 20 menos 20 de la siguiente manera […]:

20 menos 20 … tú ya sabes.

En otro problema […] pone en lugar del cero como resultado […], simplemente:

El trigo se acabó.

Los indios expresaban, hace ya 1,500 años, con la palabra sanscrita “śūnya” no tan solo el número cero, sino que también el concepto de “el vacío”. La traducción de esta palabra al árabe es “Sifr”, a partir de esta traducción se deduce nuestra palabra “cifra”. Además, Sūnya significa en latín “zephirum” o “zephiro”, de donde provienen las palabras en inglés “zero”, del francés “zéro” y del español “cero”. Entonces, se debería agradecer y reconocer a los indios el descubrimiento y uso del cero en sus tres áreas (^{Guedj, 1997}) relativo al sistema posicional, como número y como cantidad del conjunto vacío.

El matemático árabe-persa Muhammad ibn Musa al-Khwarismi (ca. 780 - ca. 850) escribe sobre la utilización del cero, por los árabes, para el concepto de nada, este era representado por medio de un símbolo parecido a letra minúscula “o”. Este símbolo fue utilizado como “cero” casi en todas partes de la India, en el norte y en el sur de la India, como también en el sur de Asia.

Recién en el siglo XII, fue introducido el cero en Europa y de allí para el occidente. Antes de este tiempo y con el uso del ábaco, el cero no era necesario (^{Guedj, 1997, p. 532}). En la tercera mitad del medioevo, se reemplazó el uso del ábaco por medio de los cálculos simbólicos. Con la “caída” del ábaco nace una nueva forma de la aritmética, según algunos más elegante y eficiente. Esta nueva forma de hacer cálculos se deriva directamente de los procesos de cálculo de los indios y de los árabes, se le dio el nombre de “Algorismus” (hoy en día “Algoritmos”), por Al-Khwarismi uno de los primeros en enseñar estos procesos de cálculos a otras personas.

La importancia del símbolo cero en el mundo moderno es indiscutible, se puede encontrar en cada texto escolar y en cada texto universitario relacionado con matemática o disciplinas afines, aunque, por mucho tiempo, su existencia no era completamente comprensible. Es recompensable y para muchos necesario, observar más precisamente este concepto de “nada” o de “cero” desde diferentes perspectivas.

NEUTRALIDAD

Una de las características del cero es que tiene un comportamiento que se muestra en relación con otros números y bajo alguna de las operaciones aritméticas. En el caso de la adición, el cero es tratado como “neutro”, es decir un objeto que se comporta de manera neutral frente al resto, es imparcial, no aumenta ni disminuye al objeto con el cual está siendo relacionado.

En matemática, se dice que un elemento se llama neutro si al ser operado con otro elemento, este conserva su valor. Cuando se hace la operación con el neutro, no hay cambio. Ahora, si se considera la multiplicación, podemos observar que el cero no se comporta de manera neutral, sino que más bien se comporta como un anulador de números y que transforma todos los números en nada.

En el caso del conjunto de los movimientos isométricos, traslaciones, rotaciones y reflexiones de una figura bidimensional o tridimensional, el elemento neutro sería una doble reflexión, una rotación en 0° (múltiplos de 360°) o bien la ausencia de movimiento. En este caso, el cero es una encarnación de lo estático: nada se mueve, todo se mantiene o todo vuelve a su estado inicial. En el caso de los múltiplos de 360°, la figura vuelve al estado inicial una y otra vez, con esto se tiene una clase de movimientos que corresponde a la rotación en 0°. Lo estático es una noción cíclica donde la neutralidad se repite.

Otro aspecto de la neutralidad del cero, donde el objeto matemático no cambia y el cero se comporta neutralmente, se tiene al observar el número 008765. En este caso, se puede ver inmediatamente que el cero no afecta en nada, se comporta neutralmente o bien que no “sirve para nada”. La expresión “eres más inútil que un cero a la izquierda”, indica que poner un cero a la izquierda no sirve para nada. El uso del cero a la izquierda no cambia el valor del número ya que en el sistema posicional se está poniendo una cifra que corresponde a la ausencia de una cantidad. En el caso de una cuenta bancaria, se tiene la visión de código numérico y no indican en este caso una cantidad.

Si se ubican algunos ceros en el lado derecho de un número, en nuestro caso 876500, entonces se aumenta en múltiplos de 10, 100, 1000, etc., el valor del número. Tenemos todo lo contrario a un comportamiento neutral del cero, la cantidad se potencia en múltiplos de diez. Es nuestro sistema decimal y la notación en este sistema, permite hacer una diferencia en relación a un comportamiento neutral del cero a la derecha o a la izquierda, es la convención que se tiene para representar números y leerlos.

Los significados de neutralidad del cero que hemos visto en esta sección tienen características completamente diferentes. Por un lado, ser elemento neutro dentro de una estructura algebraica y por otro lado en la forma de escribir un número dentro del sistema decimal. El elemento neutro es clave dentro de la definición de un “Grupo” y dentro de esta misma definición se puede diferenciar en estructuras algebraicas con conjuntos numéricos o bien con conjuntos de movimientos.

LAS TRES ETAPAS DE DESARROLLO DEL CERO

El cero es conceptualmente diferente al resto de las cifras 1, 2, 3, ..., 9 de nuestro sistema decimal. Como ya lo mencionaba el matemático Pierre Laplace,⁴ “el cero es una idea tan sencilla, que su propia simplicidad es la razón por la cual no somos lo suficientemente conscientes de la admiración que se merece”.

El cero ha recorrido un largo camino para llegar al significado que le damos hoy en día y debió pasar por una evolución en forma de tres estadios: en el primer estadio es funcional, en el segundo estadio es un dígito y en el tercer estadio es un número. En su primer estadio el cero es utilizado como símbolo y no como número (^{Guedj, 1997}), es utilizado de manera funcional para expresar que la cantidad que se encuentra a la izquierda de este ha sido aumentada en 10. Esto significa que la expresión 20 se entendía como diez veces dos, cada vez que se agregaba este símbolo el valor era multiplicado por diez. En este caso, el cero se utilizaba como un símbolo para expresar un proceso multiplicativo en decenas, centenas, miles, etc.

En el segundo estadio el cero es tratado como un dígito (del inglés: digit) o como una cifra más de las nueve que ya existían, evolucionó junto con el conteo de los dedos de la mano y su desarrollo termina con el sistema decimal. Al contar los diez dedos de la mano, se obtiene 10, al contar dos veces los dedos de las manos se tiene 2 veces 10 que es 20, etc. Esta forma de contar y de expresar las cantidades, de diez en diez, es la base de nuestro sistema decimal, donde el cero es considerado un dígito más.

Visualmente hablando se puede comparar este proceso con la idea de “pensar en paquetes”, donde cada paquete de diez es una unidad de medida. En el caso del número 564, se tienen 5 paquetes de 100 (10 veces 10), 6 paquetes de 10 y 4 dedos, en nuestra notación actual sería: 5 ·10 ·10 + 6 ·10 + 4 = 5 · 100 + 6·10+4=564.

El cero como dígito, no tiene un recorrido tan fácil, hoy en día nos parece natural y completamente comprensible. Esto es, porque el sistema decimal no fue el único sistema utilizado en Europa. Al inicio del siglo XIX, había diferentes sistemas en uso, uno de ellos, que aún conservamos es el sistema duodecimal (paquetes de 12) de los ingleses. Este sistema duodecimal tiene su origen en el conteo de los dobleces de los dedos sin considerar el dedo pulgar y hasta hoy en día se conserva este sistema en la unidad de medida “pulgada” (doce partes de un pie), en el antes utilizado “chelín” británico, que tenia el valor de doce “peniques” y en otros países la utilizada “docena”, que se refleja en los paquetes de doce (doce huevos, doce platos, doce botellas).

Otro de los sistemas posicionales utilizados hasta el día de hoy y que tienen su base en la cultura babilónica, es el sistema sexagesimal, con 60 unidades y para cada unidad 60 símbolos diferentes. Según este sistema se organizó la medida para el tiempo, según hora, minutos y segundos. También, se utiliza para el conteo de puntos en el tenis. Como este sistema tenía tantos símbolos era más complicado hacer cálculos, por eso la transición de este sistema al sistema decimal fue mejor recibida por el mundo entero.

Los mayas, los aztecas, los celtas y los franceses usaron el sistema vigesimal en diferentes épocas de la historia. Esto se basa en el uso de 10 dedos de la mano y 10 dedos del pie, por lo que se cuenta en incrementos de 20 unidades. Se tienen 20 símbolos para anotar y para hacer cálculos con ellos. Un ejemplo de la actualidad de este uso vigesimal se puede encontrar en la palabra francesa quatre-vingt que significa cuatro veces veinte y en el nombre que recibe el número ochenta.

A principios del siglo XX, se celebraron reuniones en la ciudad de París, para unificar los diferentes sistemas de numeración que se utilizaban, tanto en el comercio, como en el día a día en Francia. Dada la simplicidad del sistema decimal y su predominancia en el comercio, se decidió que este sistema de numeración sería el utilizado en las cuentas y anotaciones comerciales nacionales.⁵

En el tercer estadio del cero, el enfoque fue llevado hasta como se conoce hoy en día: el cero como número. Finalmente, cuando preguntamos: ¿cuánto es dos menos dos? Se puede responder cero, sin tener problemas frente a la palabra “cuánto” y confirmando que esta expresión, en última instancia, conforma el significado de número.

Cero es un número y representa una cantidad inexistente o el vacío de un conjunto o nada de elementos. El cero es considerado en el sistema de axiomas de Peano,⁶ para los números naturales (^{Kaiser y Nöbauer, 2002, pp. 133-216}):

Contar desde el cero era una práctica común en la era maya, el primer día del mes estaba representado por el símbolo cero y su dios asociado Zotz, el segundo día del mes estaba asociado por el número 1, etc. En muchos casos, cuando se habla de los números y cifras, se pone en primer lugar el cero y se termina en el nueve, contando estas cifras se tiene que el primer número natural es el cero (^{Ifrah, 1998}). Con esto el cero es considerado como el primer número natural. Sin embargo, muchos matemáticos no consideran el cero como un número natural, y solo lo permiten como un elemento del conjunto de los números enteros, donde se introduce y se usa en forma estructural.

LA POTENCIA DEL CERO

Muchas definiciones matemáticas parecen increíbles, por ejemplo, qué puede ser más increíble cuando se dice: ¡cada número elevado a cero es igual a 1! Es mucho más creíble y claro, cuando se explica que un número elevado a la tres, en símbolo a3, es una abreviatura para la expresión “a por a por a” o en símbolos a3=a×a×a. Pero ¿cualquier número elevado a cero es igual a 1? De hecho, esta es una regla que todos los matemáticos han acordado: “se define que a0=1”.

Si no fuera así, todo el constructo matemático relacionado con las potencias se derrumbaría.

Las potencias como aⁿ son una abreviatura para una cantidad n de factores del mismo número “a”. Hay un número que es denominado “base”, que es el número que se repite, y hay otro número, denominado “exponente”, que aparece un poco más pequeño en la parte superior derecha e indica el número de repeticiones que aparece “a” en la multiplicación. La base es un número que si se eleva a cero no debería anularse o convertirse en cero.

Considere la siguiente propiedad, que se enseña a nivel escolar, sobre potencias: un número “a” elevado a “n” multiplicado con el mismo número elevado a “m” es igual a el mismo número “a” elevado a “n + m”, en símbolos: an∙am=an+m. Esta propiedad es utilizada para explicar por qué un número elevado a la cero debe ser 1, ya que si consideramos en esta propiedad el valor m = 0, se puede ver qué an=1 y que el producto an∙1 es igual a “an”. Además, se tiene que an+0=an, porque el cero es el neutro de la adición, esto está lejos de ser una demostración del porqué un número elevado a cero es igual a 1.

Para explicar la propiedad a0=1 para cualquier número “a”, se necesita una noción informal de lo que es una función continua.⁷ Consideremos la base 12 y diferentes exponentes. El número que se obtiene cuando se eleva 12 a un número positivo muy grande es un número positivo muy pequeño. En cambio, si 12 se eleva a un número negativo (muy pequeño) como exponente, se obtiene un número positivo muy grande.⁸

Si consideramos una base constante y valores reales variables para el exponente, se escribe simbólicamente lo anterior como la función f(x)=(1/2)x, x∈R. Se sustituyen valores para que están muy cercanos al cero como, por ejemplo -0,001 y 0,001, así se obtiene en el primer caso el valor de 1.0007 y en el segundo caso 0.99931. En ambos casos o mejor dicho desde la izquierda y desde la derecha el valor se aproxima al número 1. Como se trata de una función continua, no hay saltos y se tiene que debe existir un determinado valor para tal, que el valor de la función sea 1.

Esto ocurre exactamente en el momento en que el exponente es igual a cero (x=0). Cuando se hace la gráfica de la función f(x)=(1/2)x, x∈R se obtiene la figura 1, donde se puede observar la relación entre la función continua y la proposición: todo número elevado a la cero es igual a uno. En particular, 12 elevado a la cero debe ser igual a 1.

Figura 1 Gráfico de la función f(x)=(1/2)x, x∈R  

El caso en que el cero sea la base, es esencialmente más complicado: ¿es cero elevado a cero igual a 1 o es igual a cero? O bien se obtiene algo completamente diferente.

Hasta el inicio del siglo XIX muchos matemáticos ponían simplemente 00=1, sin preguntarse si esta expresión tenía sentido o precisión matemática. Cauchy⁹ fue el primero en listar las expresiones indeterminadas como 00 y 0/0. Hubo dos intentos, sin éxito, de considerar cero elevado a la cero como 1. En 1833, se presentó un documento con pocos argumentos convincentes sobre cero elevado a la cero igual a uno. Luego de esto, los trabajos presentados consideraban mucho de la teoría desarrollada por el matemático Pfaff,¹⁰ donde era utilizado el valor del límite para probar que 00=1, estos trabajos fueron rápidamente refutados con un contraejemplo.

El segundo caso, el informático Knuth¹¹ se refirió a esta controversia en la revista American Mathematical Monthly de 1992 y rechazó firmemente la conclusión de que cero elevado a cero era indefinido. Si no se puede suponer que 00=1, muchos teoremas matemáticos requieren un tratamiento especial para el caso 00 y como informático era necesario tomar una posición. Sin embargo, la mayoría de los matemáticos (a diferencia de los científicos informáticos) prefieren la declaración de Cauchy que 00 es una expresión indefinida.

EL SISTEMA BINARIO (SIN COMPUTADORES SIN EL CERO)

Sin darnos cuenta, la mayoría de nuestra vida moderna se basa en un sistema binario, un ejemplo lo tenemos cada vez que se elige entre “sí” o “no”. Aunque los humanos a menudo usan la tercera opción, “tal vez”, una computadora solo distingue entre los dos estados “fluye” y “no fluye”, representados por los números 1 y 0. El sistema binario matemático utiliza solo los dígitos 0 y 1, es el sistema con más importancia y el más simple posible (^{Guedj, 1997}).

Este sistema posicional es a la vez el más antiguo y el más moderno, que sigue siendo utilizado. La versión más antigua que es conocida, proviene de las islas del estrecho de Torres, entre Australia y Papa Nueva Guinea. Sus habitantes usan un método de conteo llamado “urapunokosa” caracterizado por el uso de dos números:

1 = urapun

2 = okosa

3 = okosa-urapun

4 = okosa-okosa

5 = okosa-okosa-urapun

6 = okosa-okosa-okosa

... etcétera. (^{Guedj, 1997, p. 59}).

En el año 1703, el filósofo y matemático alemán Gottfried Willhelm Leibniz¹² dijo que prefiere el sistema binario al sistema decimal, indica que es suficiente para la ciencia de los números. Solo utiliza los dígitos 0 y 1 y para llegar al número dos, uno se mueve un lugar hacia la izquierda y comienza una nueva columna, es decir, en lugar de 2, se escribe 1 0 y en lugar de dos por dos, es decir 4, se escribe 1 0 0; analógicamente se obtiene que dos veces dos veces dos, es decir 8, el número binario 1 0 0 0. Las posiciones del sistema binario, pensando en moverse de dos veces dos, están definidas por potencias de dos. El número 3 en el sistema binario se representa por 1 1, lo que resulta de 1×2+1×20=3. El número 5 se escribe entonces 5=4+1 o igual a 1×22+0×20=5, luego se representa por 1 0 1 en el sistema binario. Siguiendo este modelo todos los números naturales pueden ser representados con 0 y 1.

La longitud de la notación binaria está en desventaja con la notación decimal y representa un inconveniente para las personas. Para representar los dos dígitos en el número decimal 69 en binario, se necesitan siete posiciones: 1 0 0 0 1 0 1.

EL CONJUNTO VACÍO

Una definición clásica de conjunto es que este representa una combinación de ciertos objetos distinguibles dentro de un todo; los objetos se llaman elementos del conjunto y el todo se denomina universo. En este sentido, también se puede definir un “conjunto falso” que no contiene ningún elemento u objeto. Este conjunto se denomina conjunto vacío y se utiliza el símbolo “∅” para denominarlo. Para indicar la cantidad de elementos de este conjunto se utiliza el cero.

Lo más interesante de esta definición, es que el conjunto vacío está contenido en cualquier otro conjunto de objetos. Supongamos que el conjunto vacío no es un subconjunto de un conjunto arbitrario A, en notación simbólica ∅⊆A. Esto significa que hay al menos un elemento del conjunto vacío que no está en el conjunto A, lo cual es imposible porque el conjunto vacío no tiene ningún elemento. Así, la afirmación: el conjunto vacío es subconjunto de cualquier conjunto A, en símbolos ∅⊆A, debe ser correcta para todos los conjuntos. Esto quiere decir que la nada está contenida en todas partes.

Otra definición del conjunto vacío es: un objeto es un elemento del conjunto vacío, solo si este es diferente de él mismo. En notación matemática ∅=x∈U/x≠x, donde U es el conjunto universal para el cual la proposición x≠x es verdadera, como no existen tales elementos, el conjunto ∅ está vacío, sin elementos.

Aquí, podemos establecer una primera relación entre el infinito y el conjunto vacío. El cuarto axioma de Zermelo¹³ permite relacionar los conjuntos potencia¹⁴ del conjunto vacío con los números naturales. Se puede formar un conjunto potencia, realizando de manera sucesiva potencias del conjunto vacío ∅. El primer paso es P(∅)={∅}, en el siguiente paso se forma el conjunto potencia del conjunto vacío, es decir, el conjunto vacío y el conjunto completo PP∅=∅,∅. Para la segunda iteración, se tiene: PPP∅=∅,∅,∅,∅, notar que hay intersecciones que son vacías o el mismo conjunto.

Si se continúa haciendo las potencias del conjunto vacío, se obtiene la sucesión denominada por Zermelo Z0=∅,∅,∅,∅,∅,∅,∅,∅,.... Considerando el cardinal del conjunto ∅ igual cero, {∅} como 1 y ∅,∅ como 2, etc., se obtienen todos los números naturales (^{Ebbinghaus, 2007}). Obtenemos que ¡el cardinal del conjunto vacío permanece siempre igual a cero y el cardinal del conjunto Z0 de Zermelos es infinito! Es decir, a partir del conjunto vacío y sus potencias, se puede formar “desde la nada o sin nada” un nuevo conjunto que tiene infinitos elementos.

¿HASTA DÓNDE NOS LLEVA EL CERO?

En muchos países, se enseña a resolver ecuaciones de segundo grado, una manera de enseñar es utilizando una fórmula que debe ser conocida y aplicada para encontrar las soluciones (cuando las hay). En el sur de Alemania, esta fórmula tiene incluso una expresión conocida como “Mitternachtsformel”, que en español sería “la fórmula de medianoche”. Esta expresión indica que los estudiantes deben poder recitarla, incluso si el profesor llama a medianoche.

¿Cuál es la expresión matemática para esta fórmula ominosamente importante? Aquí está:

Por medio de la sustitución de los valores correspondientes se obtienen las dos soluciones x1 y x2 de una ecuación de segundo grado de la forma:

Las soluciones obtenidas por la fórmula, son los valores de x para los que esta expresión resulta cero. De hecho, no hay una fórmula comparable para solucionar ecuaciones de primer o quinto grado. Si uno fuera a buscar la solución de la ecuación:

lo primero que se debe hacer es igualar a cero, para esto se debe restar 7 en ambos lados de la ecuación, obteniendo:

Evaluando para los valores a, b y c, se obtiene que las dos soluciones son:

Los valores x1=2 y x2=-2,5 se llaman los ceros de la función cuadrática f(x)=2x2+x-10. De manera ilustrativa en la figura 2, estas soluciones denotan los lugares donde el gráfico de esta función se intersecta con el eje X.

Figura 2 Gráfico de la función f(x)=2x2+x-10  

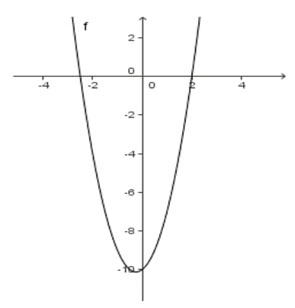
Es fácil visualizar que las funciones cuadráticas (llamadas parábolas) pueden tener como máximo dos ceros, un cero doble o ningún cero. Si el vértice de una parábola abierta hacia arriba tiene su vértice debajo del eje X, entonces hay dos ceros diferentes, si el vértice está justo sobre el eje X, entonces hay un cero doble, y si el vértice está por encima (debajo) del eje X, entonces no hay ceros para esta función. Esto se aplica en general a la gráfica en el sistema de coordenadas de todas las funciones polinomiales de grado n (donde xn es la mayor potencia de x) donde la gráfica se intersecta a lo más n veces con el eje X.

No se puede estar completamente satisfecho, con el hecho de que no hay un cero cuando el vértice de la parábola se encuentra sobre (debajo) el eje X. Si la función es x2+1, el vértice está encima del eje X y así no hay ceros de la función. Se puede insistir matemáticamente y afirmar que uno no tiene los números apropiados para describir estas soluciones. Este fue el caso de Descartes,¹⁵ Euler¹⁶ y Gauss¹⁷ que encontraron en los siglos XVII y XVIII ciertos números que permitían determinar ceros de todas las funciones polinomiales y los llamaron números “imaginarios” o “complejos”.

En este nuevo mundo de números la función x2+1 tiene dos ceros: +i y -i, ambos números representan a la raíz de -1. ¡Estos números son realmente imaginarios! Leibniz incluso creyó que el número i era una mezcla de ser y no ser, y comparó el número i con el Espíritu Santo debido a su existencia etérea.

Una de las proposiciones más importantes de la matemática, se basa en este conjunto de números imaginarios, el teorema fundamental del álgebra, demostrado por Gauss en 1799: cada polinomio de grado n siempre tiene exactamente n ceros complejos. El hecho de que estas soluciones sean a veces puramente imaginarias es solo un aspecto caprichoso del cero.

Un número dividido por cero se convierte en una fracción cuyo denominador es cero. Esta fracción se identifica con el conjunto infinito. En este conjunto, que consiste en tener al cero como su divisor, no hay cambio, aunque se pueden agregar o restar muchos números; al igual como no hay cambio en el Dios infinito e inmutable, cuando los mundos son creados o destruidos, aparecen o desaparecen numerosas órdenes de seres.¹⁸

Si miramos el símbolo a0, donde “a” es cualquier número, sería válido, según Bhāskara que a0=∞. ¿Es esto realmente así?

Elijamos concretamente para “a” el número 1 y consideremos la función f:R→R,x→1x, a todo número real x le asigna su inverso multiplicativo (0 no tiene inverso multiplicativo). Entonces los valores de f(x) son cada vez más grandes para valores siempre más pequeños de x:10,1=10, 10,01=100, 10,001=1000, etcétera.

El problema para esta historia es que en este proceso no estamos realmente dividiendo por cero, nos estamos aproximado a dividir por cero. En otras palabras, si permitimos que x llegue a cero, entonces el límite de la función es infinito, en notación simbólica: limx→0⁡1x=∞ (“lim” es la abreviatura para la palabra “Limes”, del latín “límite”).

En el siglo IX, los indios descubrieron que un número multiplicado por cero da cero, esto recuerda a la frase, muy citada y criticada, de Martin Heidegger, “la nada nihiliza” o bien “la nada destruye”. En consecuencia, si tenemos 5⋅0=0 y 13⋅0=0 ambos dan el mismo resultado cero. Ahora, si la división por cero estuviera permitida, entonces obtienes 5∙00=13∙00. En la escuela, al calcular con fracciones, aprendes que puedes simplificar factores iguales. Simplificamos los ceros y obtenemos que 5=13. Esta es una contradicción obvia, por lo que debemos concluir que no se permite dividir por cero.

El símbolo a0 no tiene ningún significado. Lo que se podría haber aclarado también con decir que no se puede hacer el proceso de dividir una cantidad entre otra cantidad, donde no hay cantidad para dividir.

EL CÁLCULO INFINITESIMAL Y LA INCLINACIÓN DE UN PUNTO

Un gran tema de la matemática es la llamada “discusión de la curva”, donde las funciones se examinan por sus propiedades, se calculan los ceros y se grafica la función en un sistema de coordenadas. Para resolver problemas de modelación, es necesario conocer a cabalidad la función y hacer una discusión basada en el cálculo infinitesimal y la derivada.

La discusión de la curva se agota en las transformaciones algebraicas y tiene una interpretación geométrica visual, que fue el punto de partida histórico de la derivada. La pregunta que históricamente se quiere responder es: ¿cómo determinar el tipo de tangente a una curva en un punto particular?

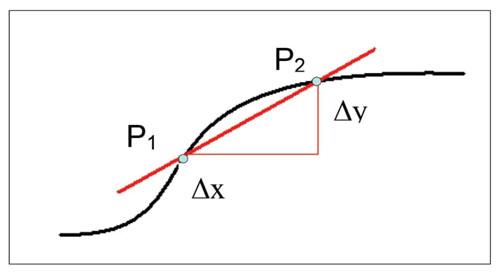
Para determinar la ecuación de esta recta tangente es necesario encontrar la pendiente m, ver figura 3. La pendiente se calcula a través del cociente m=ΔyΔx, entre la “diferencia de la altura” ∆y y la “diferencia del segmento horizontal” ∆x entre dos puntos P1 y P2 que están sobre la curva.

Figura 3 Curva y búsqueda de la recta tangente a P1. 

Como se muestra en la figura 3, tenemos una mala aproximación para la inclinación de la tangente que pasa por el punto P₁ , para obtener una mejor aproximación, se debe acercar el punto P₂ hacia el punto P₁, esto significa reducir la distancia entre los puntos a cero. 0

La pendiente en un punto sería 00, pero ya sabemos que esta expresión no tiene significado o bien, que puede ser cualquier número. Una vez más, el cero nos da un nuevo acertijo, que tiene respuesta, ya que obviamente se puede encontrar la pendiente de la tangente en cada punto de la curva.

La solución la encontraron de forma independiente Isaac Newton¹⁹ y Gottfried Leibniz. Newton utilizó un truco ingenioso como remedio contra la división prohibida: agregó a un cambio (infinitesimalmente pequeño) 0∆x , donde la magnitud describe un periodo de tiempo ominoso casi igual a cero, pero no del todo igual a cero. Notar la similitud del símbolo con la forma de escribir cero de los árabes.

Al final de los cálculos, esta magnitud quedaba fuera, por lo que nunca se necesita saber su valor exacto. En lugar de ver ΔyΔx observaba 0∙Δy0∙Δx y simplificaba cuando era necesario. Básicamente, Newton no había solucionado realmente el problema 00, especialmente porque su magnitud tenía un carácter muy extraño. Newton mismo decía que era muy desagradable, a veces el símbolo se comportaba como un cero y otras veces como un número cualquiera diferente a cero.

^{Seife (2002, p. 137)} escribe al respecto:

De cierta manera, fueron esas infinitesimales magnitudes infinitamente pequeñas, más pequeñas que cada número positivo que uno podría haber considerado, pero fueron de cierta manera más grande que cero. Para los matemáticos de ese tiempo, esto era una idea irrisoria. Las magnitudes infinitesimales en sus ecuaciones eran embarazosas para Newton, y las barrió bajo la alfombra lo más pronto que pudo.²⁰

Lo contradictorio de esta historia, es que a pesar de todas las deficiencias, este procedimiento funcionaba. Fue Leibniz, quien tomó la “maldición” de los tamaños infinitesimales, escribió con sus propios símbolos dy y dx, y los consideró como “números” realmente existentes en matemática. Sin embargo, él no pudo solucionar en última instancia el problema 00.

La solución al acertijo vuelve a encontrar solución a la sombra del concepto “límite”. Para determinar la inclinación de la tangente, se considera que ∆x y ∆𝑦 no son realmente cero, sino que más bien “se les hace tender a cero”. Esto mismo se puede traducir matemáticamente, al límite del cociente ΔyΔx, en símbolos lim∆x→0⁡ΔyΔx, separando el proceso de su objetivo, no estamos dividiendo por cero, sino que se puede calcular de manera puramente formal ΔyΔx dejando que ∆x se vaya hacia el cero.

Si bien a primera vista, esto puede parecer una sutileza o quizás incluso tan místico como el oscuro de Newton, tenemos aquí que esta cadena de pensamientos cumple con las estrictas leyes de la matemática. El concepto del valor del límite tiene un fundamento matemático seguro y evita hábilmente los peligros que emanan de símbolos tales como 00.

LA FÓRMULA MATEMÁTICA MÁS BELLA DE TODAS

^{Hardy (1940)} compuso uno de los primeros poemas relativos a la belleza de la matemática. En 1990 la revista The Mathematical Intelligencer propone a sus lectores una evaluación de la belleza de 24 teoremas y demostraciones. El primer lugar fue para la formula eiπ+1=0, presentada por el matemático Euler, por relacionar de forma compacta las constantes más importantes del análisis, incluyendo por supuesto, nuestro controversial número cero.

Belleza significa en matemática frecuentemente sencillez, orden o coherencia (^{Inglis y Aberdein, 2014}). Detengámonos por un momento, en la más bella de todas las fórmulas. ¿Qué elementos importantes reúne? Por un lado, está el número “ℯ” de Euler, que junto con “pi”, el número más famoso y pariente de “ℯ”, un número trascendental, que quiere decir que no puede construirse con compás y regla como una longitud, ni es la solución de una ecuación algebraica. Estos números no pueden expresarse mediante un corte o ser obtenidos con una raíz. Coloquialmente, se puede decir que una persona nunca puede escribir en extenso estos números trascendentales, es decir, solo se tendrán aproximaciones a ellos y expresiones simbólicas, como letras.

Los números ℯ y están acompañados por el número imaginario i. En matemáticas, un número imaginario, es un número, cuyo cuadrado es un número real negativo. El número imaginario i, llamado también unidad imaginaria, es igual al símbolo -1. Según la opinión de Girolamo Cardano (1501-1576), tales números no pueden existir, por lo que solo son imaginarios.

Gauss encontró una representación gráfica para los números imaginarios. En su plano Gaussiano los números imaginarios forman una línea perpendicular con relación a la línea recta horizontal de números reales exactamente a través del 0. Todos los puntos de este plano forman los números complejos como un par de coordenadas, la primera es la coordenada real (eje X) y la segunda es la coordenada imaginaria (eje Y). El número complejo i se corresponde al número real 1 en el eje vertical, o el par (0|1) corresponde a 0 + i, el número 0 es el único que repite doblemente y manteniendo su rol (0|0).

Volviendo a nuestra bella fórmula eiπ+1=0, vemos que sucede algo muy extraño: agregamos 1 a la potencia de un número trascendental donde, además, el exponente es un número imaginario multiplicado por otro número trascendental, (indescriptible numéricamente) y obtenemos… ¡nada! Este hecho es, por decir lo menos, increíble, sorprendente, maravilloso y al mismo tiempo tan simple, conciso y claro, que con razón ocupa el trono de las más hermosas de todas las fórmulas.

LA ESFERA DE RIEMANN

Todos los escolares aprenden y trabajan durante su época de estudios con los elementos básicos de la simetría. Ya en la escuela primaria comienza este proceso con hechos simples como la reflexión en un eje, se dibujan figuras como mariposas, caras y figuras geométricas sencillas o se trabaja con un espejo o con pintura y papel, marcando el eje o haciendo un doblez para hacer coincidir los puntos simétricos. Este es un primer nivel, el cual es superado cuando se ven otro tipo de reflexiones, por ejemplo, reflejar sobre un círculo en vez de una línea recta. Este tipo de reflexiones se trabaja en los últimos años del colegio o en la universidad.

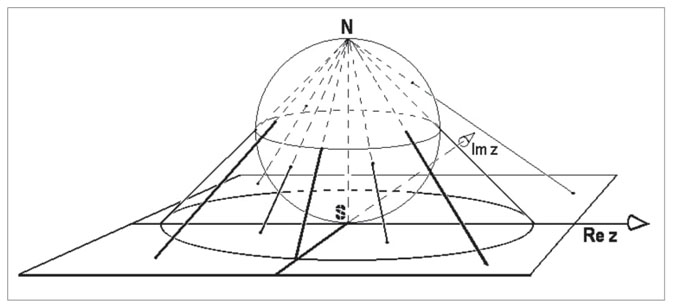
¿Cómo nos podemos imaginar esta reflexión? Consideremos nuevamente el plano Gaussiano de números reales y complejos, realicemos una “inversión” de un punto: la nueva distancia al punto cero es el recíproco de la distancia original y el ángulo es el negativo del original. Al final, es intercambiado el interior de un círculo de radio 1, el denominado círculo unitario, con el exterior del círculo; cada punto del círculo queda fijo, como se muestra en la figura 4.

Figura 4: Plano de Riemann. 

Aquí ocurre algo sorprendente: las líneas rectas que están fuera del círculo “espejo” (análogo al eje de reflexión) son reflejadas en círculos dentro del círculo de reflexión y viceversa. Con esto, las dos figuras rectas y círculos son llevadas dentro de un contexto a un par de coordenadas. Con esta reflexión circular, el trabajo de los matemáticos se hace más fácil, los resultados sobre rectas se pueden entender como casos límites especiales de resultados en círculo considerando el radio y el límite.

Consideremos un poco más precisamente la función relacionada con la inversión compleja z→1z, una generalización de la inversión real x→1x. Se desplaza el punto z a una distancia siempre más grande (en cualquier dirección) es como si se estuviera acercando a un único punto en el infinito, denotado por ∞ y cuya imagen es el punto 0. Así, el punto ∞ satisface por definición las siguientes ecuaciones:

La diferencia con lo real es que el símbolo ∞ ya no se usa solo en conexión con un proceso de borde (límite), sino independientemente como un “punto infinitamente distante”. ¿Cómo se puede entender este significado? Riemann (1826-1866) da una respuesta hermosa y profunda, interpretando los números complejos como puntos en una esfera en lugar de puntos sobre el plano (ver figura 4). El polo sur representa el punto cero y el polo norte el punto ∞. En el centro de la esfera, se encuentra el “antiguo cero” del plano numérico, que penetra en la esfera numérica de Riemann por el ecuador.

La relación entre la esfera de Riemann y el plano numérico de Gauss se remonta al método de Ptolomeo (125 d. C.), llamado proyección estereográfica. Este método responde a la pregunta de cómo hacer un mapa plano sobre una superficie curva o bien cómo dibujar el globo terráqueo sin demasiadas distorsiones.

En última instancia, el concepto de “nada” junto con su símbolo “0” y su concepto relativo “todo” junto con su símbolo “∞”, residen en la matemática en una “morada” común que no difiere de la forma de nuestra tierra. Al igual que los polos de nuestro mundo, el cero y el infinito representan los dos polos del mundo de arte abstracto de la matemática.

ENCAPSULACIÓN

En este trabajo destacan las múltiples formas de la “nada” en la matemática. Comenzando con el símbolo hasta llegar a la cifra y terminando en el número. El cero nos permite representar una cantidad inexistente, la vacuidad e incluso la nada. Hemos visto la “nada” como un elemento neutro, que deja sin modificar objetos matemáticos. Vimos cómo el cero era el pilar de nuestro sistema decimal y una fuente de problemas para las potencias, se muestra también el papel especial de este símbolo y su relación estrecha con el uno.

Vimos que el cero, es parte del poco vocabulario del lenguaje binario como un lugar característico de una función, que debe ser estudiado por los estudiantes al final de su época escolar, ya que permite resolver problemas de modelación. Como argumento para una operación prohibida o al menos sin sentido; como parte de la más hermosa de todas las fórmulas y finalmente como el gemelo del infinito, que nos revela que no está en el mundo de los reales, sino más bien del imaginario.

La nada no es en absoluto nula o insignificante en matemáticas, ni menos en los procesos de comprender la matemática en las escuelas o universidades, por el contrario, sin este concepto no habría matemáticas como las conocemos. En el colegio se debe discutir sobre la nada y sobre los conceptos matemáticos relacionados. La nada en matemática es un concepto esencialmente creativo y proponedor de discusiones, ha provocado cambios y nuevas estructuras, es vital conocerlo y comprenderlo.